解决柔性车间作业调度问题的侦查包围搜索算法*

刘　韵，胡　毅，房　超，罗　企

(1.中国科学院 沈阳计算技术研究所,沈阳　110004;2.中国科学院 沈阳计算技术研究所有限公司,沈阳　110004;3.沈阳高精数控技术有限公司,沈阳　110168)



解决柔性车间作业调度问题的侦查包围搜索算法*

刘韵1,2，胡毅2,3，房超1,2，罗企1,2

(1.中国科学院 沈阳计算技术研究所,沈阳110004;2.中国科学院 沈阳计算技术研究所有限公司,沈阳110004;3.沈阳高精数控技术有限公司,沈阳110168)

车间作业调度算法是影响车间生产效率的重要因素之一。由于调度算法属于NP-难问题，至今仍然没有办法在有限时间内找到最优解。文章提出了一种元启发式搜索方法：侦查包围算法(PEA)，通过局部搜索，旨在有限时间内最大可能的趋近于最优解。该算法吸取了禁忌搜索算法和模拟退火算法的优点，对其缺点进行改进。文中将此算法应用到柔性车间作业调度问题，阐述算法的实践。实验结果与遗传算法和禁忌搜索进行比较，证明在作业数目较大的情况下，具有良好的效果。

启发式；柔性车间; 作业调度；搜索算法；NP-难

0　引言

作为企业生产的关键环节，车间作业调度一直以来深深的影响着车间的生产效率。合理有效的调度模型以及相应的算法可以有效的提高企业的生产效率，进而降低生产成本。

经典车间作业调度问题已经吸引了无数科学家的眼球，他们同时也为解决车间作业调度问题做出了很多贡献。然而经典车间作业调度模型的许多限制，比如一个操作只能在一台机器上完成，已经不能满足现代作业车间的要求。应运而生的是柔性车间作业调度模型，它打破了作业对特定机床的限制，能够更好的模拟现代车间环境。

不论是经典车间作业调度问题还是经过改进的柔性车间作业调度问题，都被证明是NP难的问题，无数科学家为解决这个问题做出了不懈的努力，然而至今仍无法在限定时间内获得最优的解决方案。现在越来越多的研究者将目光转向启发式搜索，虽然无法给出最优解，但是有限时间内最大可能的趋近最优解，符合车间需求，可以有效提高车间生产效率。

1　柔性车间作业调度研究现状

目前的柔性车间作业调度问题的搜索算法搜索策略分为两大类[1]，即基于约束条件的搜索和基于进化的搜索。基于约束条件的搜索[2-3]是建立约束编程的基础上的，然而纯约束编程不适合解决作业数量较大的车间调度问题，不过一些改进的算法如大规模邻域搜索(LNS)[4]和迭代扁平化搜索 (IFS)[5]等有效的解决了规模限制的问题。另一种搜索策略也是当今主流的研究方向，即基于进化的搜索，主要是将作业序列编码为某种形式，通过有限次转换，最终解码得到结果。经典的主要的算法有：遗传算法(GA)[6-7]、禁忌搜索(TS)[8-9]、模拟退火算法(SA)[10]等，近些年国内外专家提出的使用蚁群优化(ACO)[11]、蜂群优化(BCO)[12-13]、人工免疫系统[14]、粒子群算法[15-16]以及多种算法结合[17]等方法，更加智能的算法也越来越多的应用到柔性车间作业调度问题。本文在实军事行动的模型基础上，提出了一种启发式搜索算法，将在下文具体叙述，并将结果与其他两种算法进行比较。

2　侦查包围搜索算法

侦查包围搜索算法是一种基于局部搜索的算法，其核心思想是进行有目的的局部搜索，通过一小部分资源去探索可能的最优解，用大部分时间去验证被探索到的地方及其周围是否存在最优解。

2.1算法思想介绍

2.1.1角色介绍

为此，我们将该算法的成分分为四个角色即敌人(E)、指挥官(C)、侦察兵(SC)以及士兵(SO)。首先，敌人代表着有威胁的位置，也即潜在的解。其次，指挥官的主要职能是接收从侦察兵发来的情报以及士兵包围过程中反馈的信息，加以分析决策，命令士兵向决策的方向前进，并为侦察兵提供一个搜索目标作为下一个目标的参考。再者，侦察兵，顾名思义其是用来侦查敌情，并向上汇报的角色，或随机或有目的地向着一个方向前进，并判断当前位置的角色有没有可能成为真正的“敌人”，有则上报，无则继续侦查。最后，士兵是该算法中数量最多的角色。士兵的主要任务是听从指挥官的命令，逐步的向敌人靠拢，行进过程中如果遇到可能成为敌人的地方，将在包围完成时向上汇报，作为侦察兵行进方向的参考。

2.1.2算法流程介绍

实现侦查包围搜索算法的前提是，对待求解的区间进行编码，形成一个作业序列排列空间，如本文中将要解决的柔性车间作业调度问题，我们将其编码为一个工序数的空间，每一个序列可能代表一个有效的解，但也可能是不满足限制条件的序列。

算法开始时，每个士兵和侦察兵都会随机分配一个空间中的点。然后，每个侦察兵会随机选择一个方向，并沿着这个方向找到一个相对较优的点作为初始侦查的点。指挥官根据收集到的侦察兵报告的方向，找出最佳的包围方向，并向士兵发送包围被选定目标的命令。士兵每当接到指挥官的命令，就从其当前所在位置，向被选定目标前进，并且记录其行进过程中遇到的“敌情”，不过，只记录比指挥官命令前往位置更好的位置。

每当士兵包围完毕，指挥官就会综合士兵提交的信息，来获取当前最有威胁的敌人，并将士兵收集上来的情报，抽取比较有威胁的部分，分别分发给每个侦察兵，作为侦察兵搜索目标的参考。侦察兵通过一定的概率选择是随机寻找方向，还是参考指挥官的情报。由于此时士兵已经高度集中，为防止过早的收敛，此时需要将士兵再次以随机的方式，分配到各个空间点。如此循环。

此算法的可以选定不同结束方式，比如根据现实情况决定，比如侦察兵的自主选择目标率p=0，限定的时间以等都可以作为算法的结束点。

2.1.3用伪代码可将算法表示如下

Step1. encode(搜索空间)

Step2. foreach 侦察兵

侦察兵.目标=p*random(搜索空间)+(1-p)*(指挥官提供的参考)//p取决于所处循环的次数，以及指挥官提供的参考的价值

侦察兵.go_to(目标)

If(侦察兵.get_better(目标)

report_to(指挥官)

Step3. foreach 情报 from 侦察兵

If better than 目标

目标=情报

foreach 士兵

指挥官.SendTo(士兵,目标)

Step4. foreach 士兵

While(not reach 目标)

士兵.MoveTo(下一维)

If((当前位置 better than 目标) and (当前位置 better than 存储情报))

存储情报=当前情报

If 存储情报！=NULL

report to(指挥官)

Step5. foreach 情报 from 士兵

指挥官.get_top_several()

指挥官.SendTo(each 侦察兵)

If(目标 better than 指挥官.最优)

指挥官.最优=目标

Loop Step2

2.1.4步骤分析

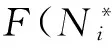
pi+1=

3　车间作业调度模型

柔性车间作业调度问题(Flexible Job shop Scheduling Problem)是n个作业任务在m台机床上执行，每个作业任务可分为k道工序，每个任务的每道工序可以再若干台机器上执行(大于等于1台)。学术界一般将柔性车间作业调度分为两类：全自由调度(每个工序都可以在任意一台机器上执行)和半自由调度(每个工序指定若干台机器)。由于后者包含前者，而且后者相对更符合真实的车间作业环境，本文选择后者为参考模型。

柔性车间作业调度的主要有三个，缩短总体执行时间，减少单个机床的工作负载，减少整个车间的工作负载。本文主要追求总体执行时间最短，另外两个目标作为参考。用数学模型可以将FJSP形式化的表示为：

(1)作业集合J={ji}1≤i≤n其中ji表示每个作业。

(2)机器集合M={mj}1≤j≤m其中mj表示每台机器。

(3)每个作业的工序的执行表示为O={oijk}其中oijk表示第i个作业的第j道工序在第k个机器上执行。

(4)每个工序在其相应机器上的执行时间可以表示为pijk其中i代表作业号，j代表工序号，k代表执行机器。

(5)Ci,max代表作业i的最终执行时间，本算法的目标是求得MIN{MAX{Ci,max}1≤i≤n}。

假设：

(1)工件的初始配置时间以及加工后移除时间不计;

(2)各机器间是相互独立的;

(3)各作业也是相互独立的;

(4)某一时间一台机器至多只能执行一个操作，而且是不可阻断的;

(5)一个作业，某一时间至多只能有一个工序在执行;

(6)不同作业的工序间不存在先后关系。

4　解决柔性作业调度问题

4.1编码

对于n个作业任务，可以将其编码为所有工序的排列组合，其中同一作业的工序之间的相对顺序保持不变，如表1所示FJSP示例，可以编码为{O113O212O122O222O231}或者编码为{O211O222O111O122O233} 等

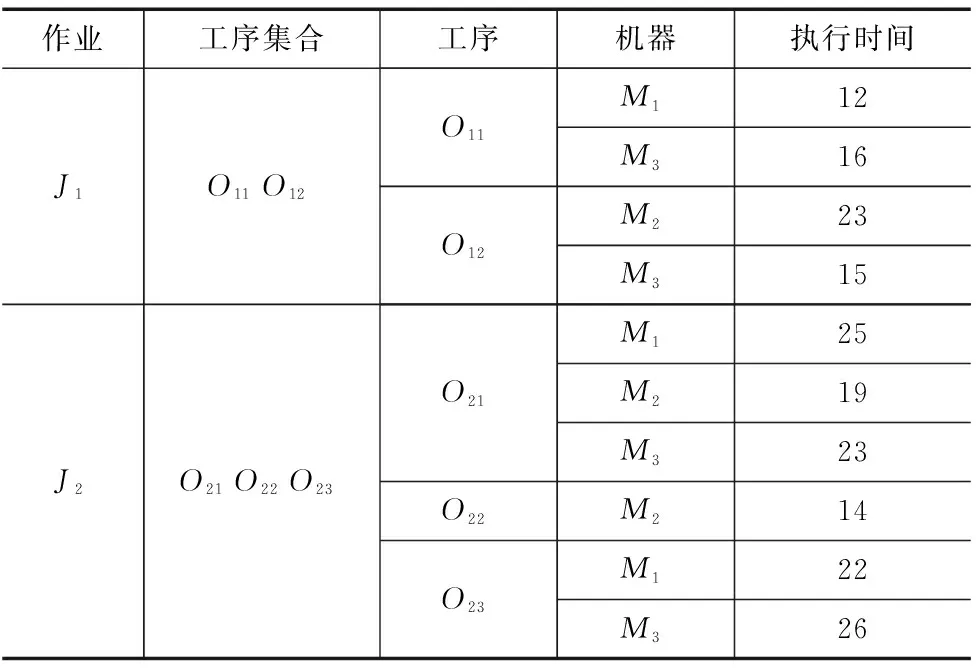
表1　2作业3机器FJSP示例

4.2算法流程

根据前文所述侦查包围搜索算法，本文将以一次包围士兵没有上报更好的位置为结束点来阐述测试侦查包围搜索算法解决柔性车间作业调度问题算法流程图如图1。

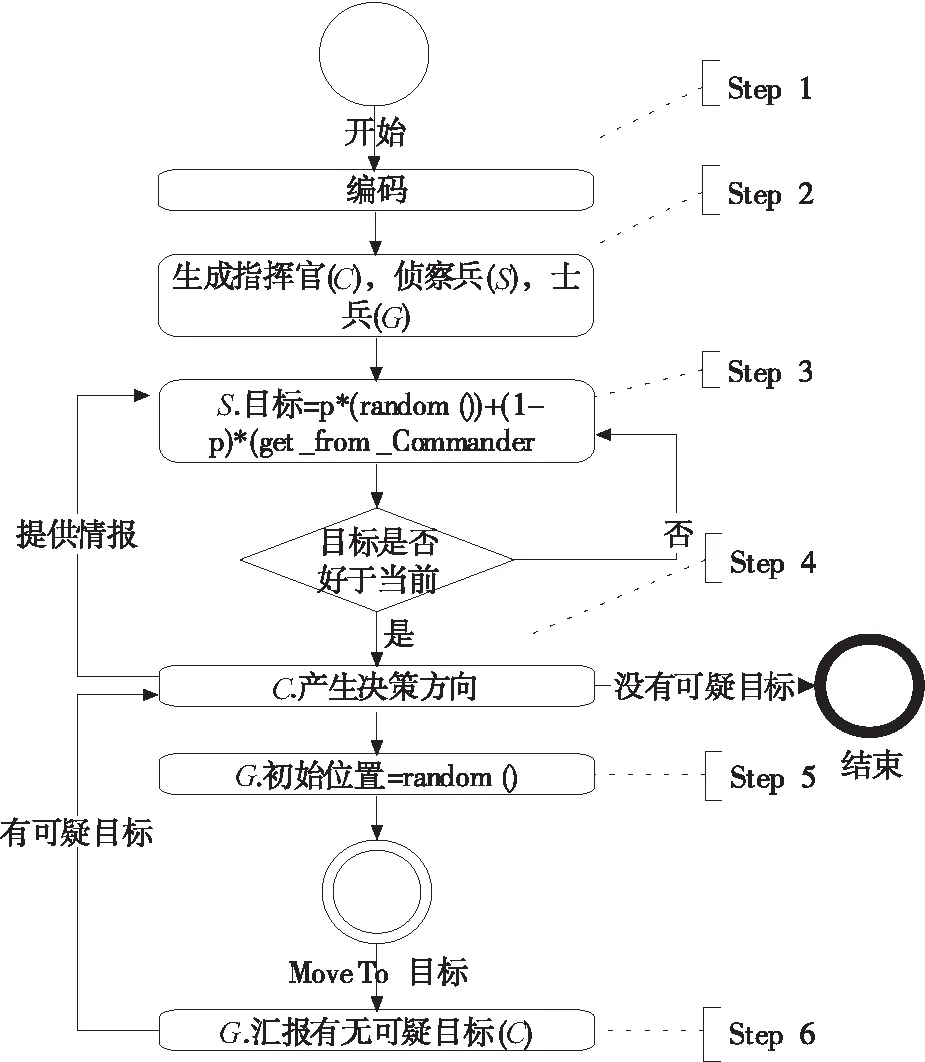
图1　侦查包围搜索算法流程图

步骤 1：为编码部分。

步骤2：产生各个角色的初始值，其中C代表指挥官，C的数量由参与算法的节点数决定，一般一个节点对应一个指挥官。S代表侦察兵，侦察兵数目不宜过多，本文取S=log(n*m*max{Ji}1≤i≤n)n,m分别代表作业数和机器数，max{Ji}1≤i≤n代表单位作业最多的工序数。G代表士兵，是算法的主力，本文选取G=2n。

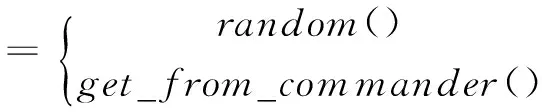
步骤4：是算法最主要部分，C从S处获取最优序列，并分发给G，同时将上一轮G上报的较优序列，选择其中靠前的分发给S。

步骤5：G利用random()随机产生初始序列，用以逐渐向目标包围，每次交换两个工序，并计算当前的序列是否满足限制条件，如果结果比目标值更优，记录等到步骤6向C汇报。

步骤 6：将G向目标移动过程中遇到可比目标更优的序列汇报给C,用以决策下轮包围方向。

5　实验结果及对比

本文的数据实验是在3.20GHz Pentium Dual-Core处理器上运行的。实验用例使用JSSP标准测试用例FT类的FT06、FT10、FT20以及LA类LA01-L20，实验输出结果是总执行时间，并与黄志等[18]禁忌搜索算法和彭传勇[19]提出的广义粒子群算法对比。

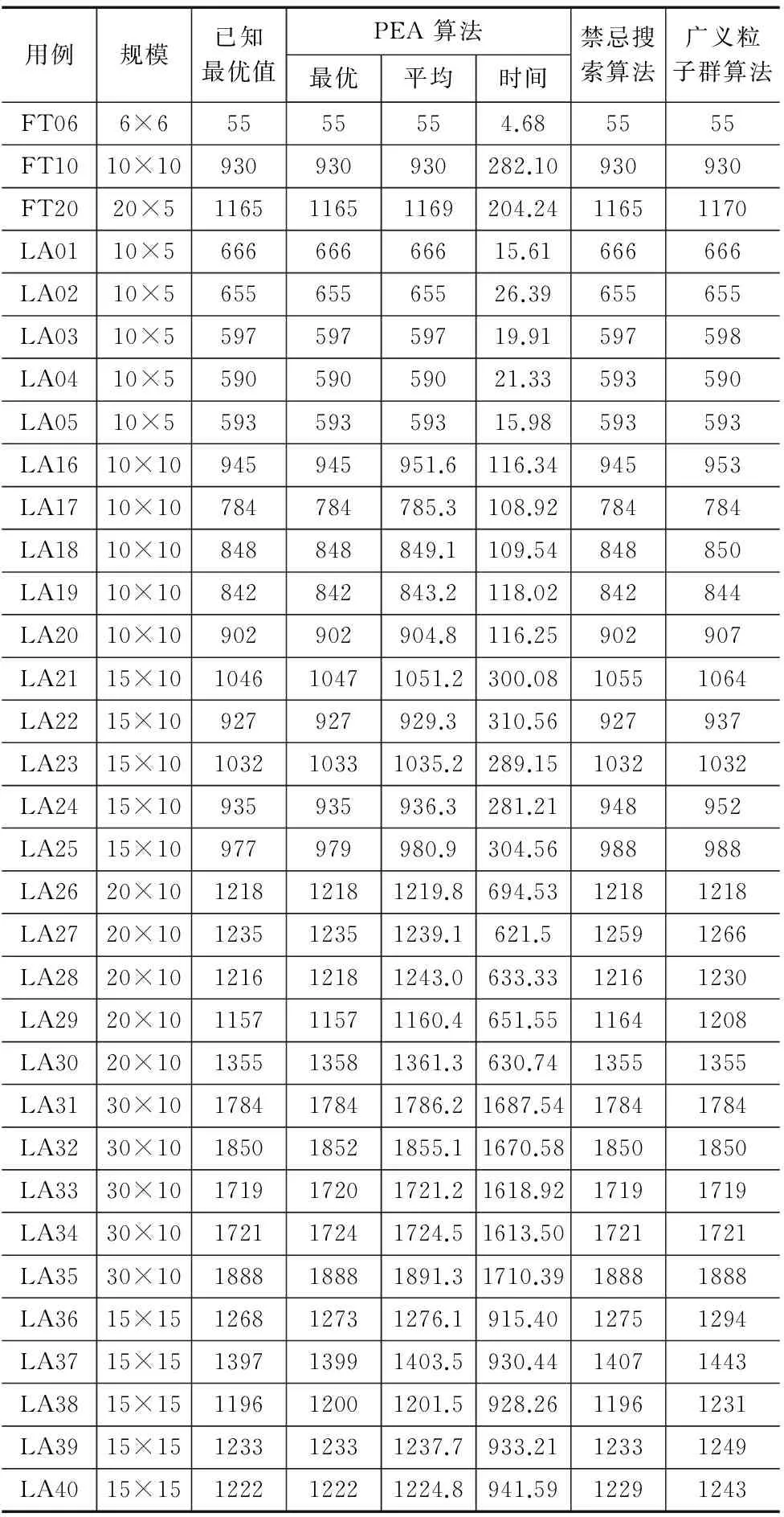
表2　PEA算法执行结果与禁忌搜索算法、广义粒子群算法比较

(1)从表2所得的数据上看，在数量级较小的LA01-LA05以及LA16-LA20测试用例上，三个算法的表现都比较不错，基本都能产生最优解。

(2)对于数量级相对较高的LA21-LA40测试用例上，PEA计算结果显示，基本与禁忌搜索算法相当，部分好于禁忌搜索算法，非常接近于已知的最优解。

(3)对于所得的结果，以FT06为例，显示如图2所示。

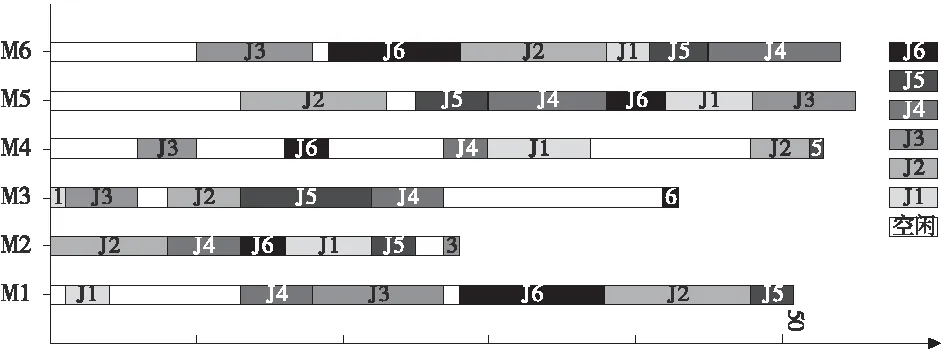
图2　FT06用例调度甘特图

6　结论及展望

本文中提出并详细介绍了一种新的局部搜索方法，并应用到柔性作业调度问题上。从上述实验证明，虽然在作业数较大情况下，包围侦察算法和禁忌搜索算法效果相当，都能达到或接近于最优解。但是随着作业数量的增加，由于该算法是建立在局部最优解的基础上，而又通过一定概率将产生随机解，作为参考因素，可以有效避免过早收敛，而更有效接近最优解。

在未来的研究中，将在以下方面继续努力：

(1)由于本算法求解全局最优解是建立在局部最优解的基础上，因而多节点协作将作为下一阶段的研究方向。

(2)对于更加宽松的条件如工序时间不确定等情况进行研究。

(3)改进搜索策略，不仅追求总体执行时间最短，更要平衡各机器的负载，以提高机器寿命。

(4)在后续实验中大量测试用例,找出最优初始值。

[1] Yuan Y, Xu H. An integrated search heuristic for large-scale flexible job shop scheduling problems[J]. Computers & Operations Research, 2013, 40(12): 2864-2877.

[2] Beck J C, Feng T K, Watson J P. Combining constraint programming and local search for job-shop scheduling[J]. INFORMS Journal on Computing, 2011, 23(1): 1-14.

[3] 武福, 张治娟. 一种求解柔性作业车间调度问题的混合智能算法[J]. 组合机床与自动化加工技术, 2013 (5):130-133.

[4] Mastrolilli M, Gambardella L. Effective neighbourhood functions for the flexible job shop problem. Journal of Scheduling 2000,3(1):3-20.

[5] Cesta A, Oddi A, Smith S. Iterative flattening: a scalable method for solving multi-capacity scheduling problems[C]. In: Proceedings of the national conference on artificial intelligence, 2000: 742-749.

[6] 李运霞, 杜娟, 孙王路. 基于多种群遗传算法的路径柔性车间调度问题[J]. 组合机床与自动化加工技术, 2014(3):152-155.

[7] Chi Q, Fu X L, Pan Y N, et al. The Optimization Model of in Job-Shop Scheduling Problem with Alternative Machines Based on Improved Genetic Algorithm[C]//Applied Mechanics and Materials,2014, 607: 569-572.

[8] Li J Q, Pan Q K, Suganthan P N, et al. A hybrid tabu search algorithm with an efficient neighborhood structure for the flexible job shop scheduling problem[J]. The international journal of advanced manufacturing technology, 2011, 52(5-8): 683-697.

[9] Meeran S, Morshed M S. A hybrid genetic tabu search algorithm for solving job shop scheduling problems: a case study[J]. Journal of intelligent manufacturing, 2012, 23(4): 1063-1078.

[10] Ma P C, Tao F, Liu Y L, et al. A hybrid particle swarm optimization and simulated annealing algorithm for job-shop scheduling[C]//Automation Science and Engineering (CASE), 2014 IEEE International Conference on. IEEE, 2014: 125-130.

[11] Yao B, Yang C, Hu J, et al. An improved ant colony optimization for flexible job shop scheduling problems[J]. Advanced Science Letters, 2011, 4(6-7): 2127-2131.

[12] Lei D. Multi-objective artificial bee colony for interval job shop scheduling with flexible maintenance[J]. The International Journal of Advanced Manufacturing Technology, 2013, 66(9-12): 1835-1843.

[13] Zhang R, Song S, Wu C. A hybrid artificial bee colony algorithm for the job shop scheduling problem[J]. International Journal of Production Economics, 2013, 141(1): 167-178.

[14] Cai B, Wang S, Hu H. Hybrid Artificial Immune System for Job Shop Scheduling Problem[J]. World Academy of Science, Engineering and Technology, 2011, 59(18): 81-86.

[15] Tavakkoli-Moghaddam R, Azarkish M, Sadeghnejad-Barkousaraie A. A new hybrid multi-objective Pareto archive PSO algorithm for a bi-objective job shop scheduling problem[J]. Expert Systems with Applications, 2011, 38(9): 10812-10821.

[16] Lin T L, Horng S J, Kao T W, et al. An efficient job-shop scheduling algorithm based on particle swarm optimization[J]. Expert Systems with Applications, 2010, 37(3): 2629-2636.

[17] Jamili A, Shafia M A, Tavakkoli-Moghaddam R. A hybrid algorithm based on particle swarm optimization and simulated annealing for a periodic job shop scheduling problem[J]. The International Journal of Advanced Manufacturing Technology, 2011, 54(1-4): 309-322.

[18] 黄志, 黄文奇. 一种基于禁忌搜索的作业车间调度算法[J]. 计算机工程与应用, 2006, 42(3):12-14.

[19] 彭传勇, 高亮, 邵新宇,等. 求解作业车间调度问题的广义粒子群优化算法[J]. 计算机集成制造系统, 2006, 12(6):911-917.

(编辑李秀敏)

Probe and Encircle Algorithm for Solving Flexible Job-shop Scheduling Problem

LIU Yun1,2, HU Yi2,3, FANG Chao1,2, LUO Qi1,2

(1.Shenyang Institute of Computing Technology, Chinese Academy of Sciences, Shenyang 110004, China;2.Shenyang Institute of Computing Technology Co., LTD. ,Shenyang 110004,China)

Scheduling Algorithm has become one of the most important factors which influence Job-shop productivity. Because of being proved as NP-hard problem, there are no Job-shop Scheduling Algorithms can achieve optimal solution. This paper proposes a meta-algorithm: Probe and Encircle Algorithm (PEA) aim to get the approximate optimum solution via local search within a limited time. This algorithm absorbs the merit of Taboo Search Algorithm (TSA) and The Simulated Annealing Algorithm (SAA), and so do avoid their flaws. A Flexible Job-shop Scheduling Problem has been solved by Probe and Encircle Algorithm which will be described in detail. Compared with GA and TS, it has been proved more effective in large scale problems.

heuristic; flexible job-shop; scheduling; search algorithm; NP-hard

1001-2265(2015)11-0124-05DOI:10.13462/j.cnki.mmtamt.2015.11.035

2015-01-27；

2015-03-17

“高档数控机床与基础制造设备”国家科技重大专项、基于二次开发平台的专用数控系统开发与应用(2013ZX04007-011)

刘韵(1990—)，男，安徽定远人，中科院沈阳计算技术研究所研究生，研究方向为数控技术，(E-mail)ahlyun@126.com。

TH165;TG506

A