使用AxiSet设备的五轴机床快速测量方法*

张　娜，郑飂默，尹震宇

(1.中国科学院大学，北京　100049；2.沈阳高精数控技术有限公司，沈阳　110168；3.中国科学院 沈阳计算技术研究所有限公司，沈阳　110168)



使用AxiSet设备的五轴机床快速测量方法*

张娜1,3，郑飂默2,3，尹震宇2

(1.中国科学院大学，北京100049；2.沈阳高精数控技术有限公司，沈阳110168；3.中国科学院 沈阳计算技术研究所有限公司，沈阳110168)

针对五轴机床受装配精度和旋转部件的影响，使机床出现结构误差造成刀具在刀位点处出现偏移，影响机床的加工精度。通过分析各项误差对刀位点的影响，建立五轴运动学误差模型，使用AxiSetTMCheck-up组件中的3D测针-球体设备，对球心进行不同角度的多次测量，根据相应的五轴进给对机床误差项进行精确求解。所采用的测量方法对建立的各类误差模型具有较好的一致性，通过对五轴运动误差的补偿不仅可以提高现有数控机床的加工精度，而且为以后多轴机床的测量提供了统一的测量基础。

AxiSet设备；五轴机床；快速测量

0　引言

无论是在机床装配制造过程的机床初始误差，还是随着机床长时间、高负载的运行，都会造成机床存在一定的平移误差和旋转误差，使得旋转轴和主轴偏离本来的位置[1-2]，从而使得用机床进行加工时，影响加工工件的精度。对五轴机床的测量，一般分为单项误差直接测量法和综合误差测量参数法。直接测量法直接测量影响机床精度的主要零件，需要分步测量，一般还需要比较昂贵的测量仪器，要求专业的技术人员，测量时间较长。综合误差测量参数法是指借助标准参考物或简单的测量仪器来获得数控机床工作空间内指令位置点与机床运动轮廓轨迹的综合误差信息的一类方法。许多设备可用于测量五轴机床的几何误差，如千分表和测试棒、双球杆等和而3D测针-球体装置[3-5]等。如西门子的SINUMERIC 840D系统具有将三维空间向量转换为实际机械轴角度计算能力的3D Tool Radius Compensation功能，所带的位置转换功能实质上是五轴的刀具补偿[6-8]。本文采用英国雷尼绍公司的能够直接测量五轴机床的整体位置误差的AxiSet工具对五轴机床进行测量，从而缩短了获取测量值的时间，提高了测量速度。根据测量所得数据进一步计算机床误差项，可用来验证五轴机床的精度或者对误差进行预测和补偿。

1　五轴机床运动学模型

任何结构的机床运动都可描述为一系列的运动副和关节组成的运动链，对于由关节连接的任意两个相近的构件i和j，固连在他们上的坐标系分别为OiXiYiZi与OjXjYjZj，根据空间运动学和齐次变换相关知识，坐标系j映射到坐标系i的变换矩阵A为：

iAj=Trans(Lij)Rot(N,φN)

其中，Lij=Lij.xi+Lij.yj+Lij.zk表示坐标系原点Oi到Oj的距离矢量，N代表旋转轴轴向，Trans和Rot是4×4的平移和旋转齐次变换矩阵。

1.1五轴机床运动学转换

五轴机床有多种不同的形式结构，五轴代表三个平动轴与两个旋转轴，根据旋转轴配置的不同，机床结构类型可分为三类：工作台旋转型、刀具旋转型和混合型。

机床处于理想工作状态下时，机床各平动坐标轴均相互垂直，运动方向与机床坐标系坐标轴方向一致，两回转轴心线垂直相交，且分别平行于所绕行的轴线。则刀具坐标系到工件坐标系的空间转换关系[9-10]表示为：

1.2五轴机床运动学误差模型

假设r为刀具坐标系中的一点，Q为工件坐标系的同一点，则[Q1]T=wAt[r1]T。但是受机床部件制造与装配精度的影响，机床旋转轴的运动会引起误差，使两回转轴心线偏离原来的位置，使得工件端的旋转轴坐标系与工件坐标系不一致，同样的主轴端的两旋转坐标系也不一致，造成刀具在加工点处出现刀位点位置误差。以下对三类五轴机床进行详细描述。

1.2.1工作台旋转型机床结构

工作台旋转型机床两回转轴均作用于工作台上，因为机床误差的存在，两回转轴轴心不一致，且与工件坐标系也不一致，刀具坐标系到工件坐标系的空间转换关系表示为：

用图1所示的坐标系描述刀具中心位置相对于工件的位置关系，工件端上的第一、第二旋转轴定义为Ns1、Ns2，分别绕X、Y、Z中任意两轴旋转，旋转角度为φs1、φs2，则wAt可表示为：

wAt=Trans(Lws2)Rot(Ns2,-φs2)×

Trans(Ls2s1)Rot(Ns1,-φs1)Trans(X0,Y0,Z0)

其中的工件坐标系w到Ns1轴的距离偏移矢量表示为Lws2，两旋转轴之间的距离偏移矢量表示为Ls2s1。

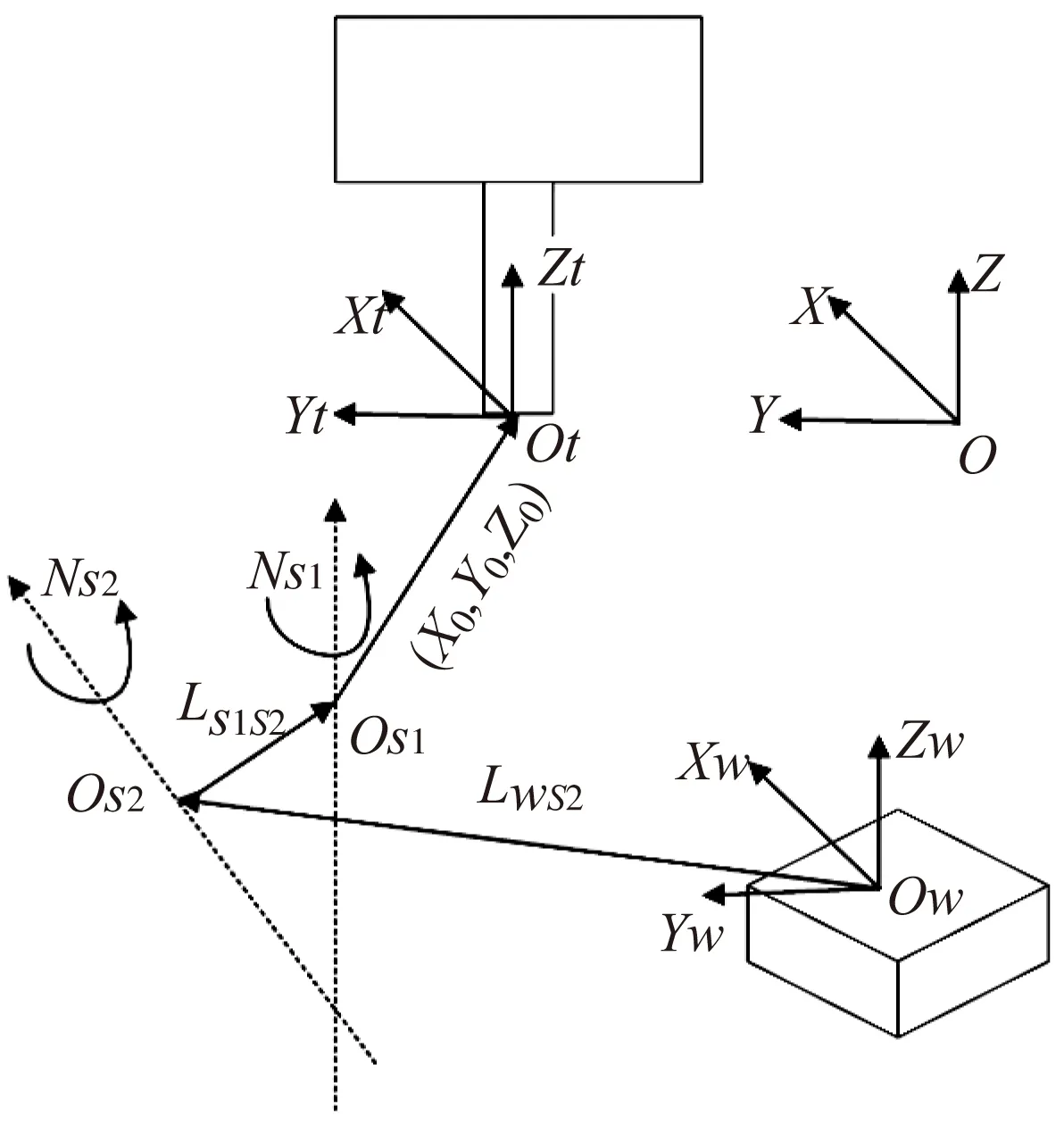
图1　工作台旋转型机床坐标系统

1.2.2混合型机床结构

混合型机床两回转轴分别作用于工作台上和主轴上，因为机床误差的存在，第一旋转轴与工件坐标系不一致，且第二旋转轴也不平行于所绕行的线性轴。刀具坐标系到工件坐标系的空间转换关系可表示为：

用图2所示的坐标系描述刀具中心位置相对于工件的位置关系，工件端上的第一转轴定义为Ns1，主轴端第二旋转轴定义为Ns2，分别绕X、Y、Z中任意两轴旋转，旋转角度为φs1、φs2，则wAt可表示为：

wAt=Trans(Lws1)Rot(Ns1，-φs1)×

Trans(X0,Y0,Z0)Rot(Ns2,φs2)Trans(Ls2t)

其中的工件坐标系w到Ns1的距离偏移矢量表示为Lws1，Ns2与主轴端点之间的距离偏移矢量表示为Ls2t。

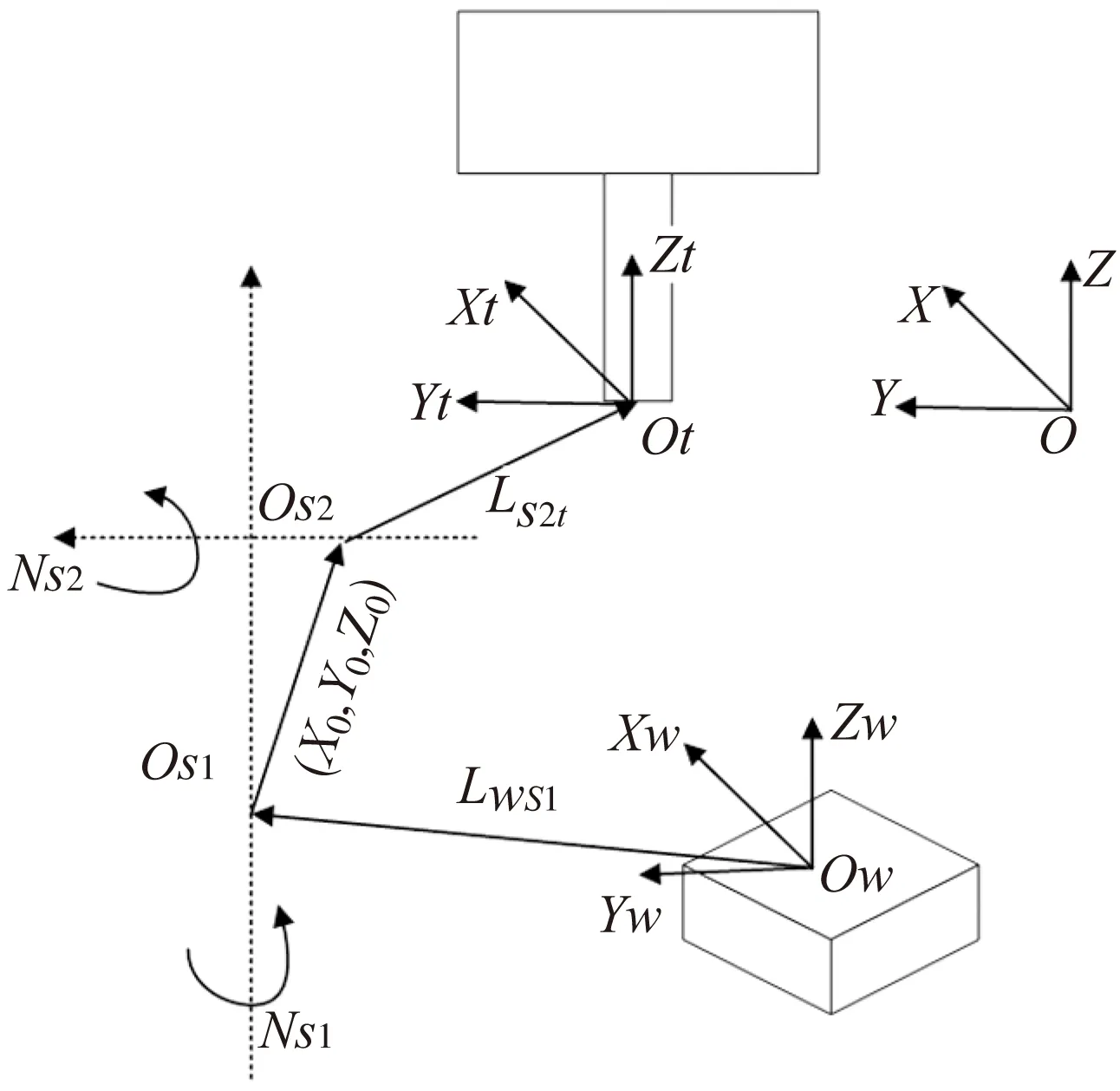
图2　混合型机床坐标系

1.2.3刀具旋转型机床结构

刀具旋转型机床两回转轴分别作用于主轴上，因为机床误差的存在，两回转轴轴心不一致。刀具坐标系到工件坐标系的空间转换关系表示为：

用图3所示的坐标系描述刀具中心位置相对于工件的位置关系，主轴端上的第一、第二旋转轴为Ns1、Ns2，分别绕X、Y、Z中任意两轴旋转，旋转角度为φs1、φs2，则wAt可表示为：

wAt=Trans(X0,Y0,Z0)Rot(Ns1，φs1)×

Trans(Ls1s2)Rot(Ns2,φs2)Trans(Ls2t)

其中两旋转轴之间的偏移矢量表示为Ls1s2，Ns2与主轴端点之间的距离偏移矢量表示为Ls2t。

图3　刀具旋转型机床坐标系

2　模型分析

由以上描述可知，三类机床结构模型相似，只是平移和旋转的顺序不同，三类机床中均存在四个误差项，分别来自于两个旋转轴的轴向误差Ns1和Ns2，以及与两旋转轴相关的工件(刀具)坐标系到旋转轴的两个位置偏移误差。

首先对工作台旋转型机床进行分析，四个误差项为旋转轴轴向误差Ns1、Ns2以及距离误差Lws2、Ls2s1。根据误差来源，Ls2s1与旋转轴Ns1和Ns2有关，Lws2与旋转轴Ns2和工件坐标系有关，因此若想得到这两个距离误差必要先求出Ns1和Ns2的值。对于混合型机床的四个误差项分别为轴向误差Ns1、Ns2以及距离误差Lws1、Ls2t，其中Lws1与Ns1有关，Ls2t与Ns2有关。而刀具旋转型的四个误差项为轴向误差Ns1、Ns2以及距离误差Ls1s2、Ls2t，Ls1s2与旋转轴Ns1和Ns2有关，Ls2t与旋转轴Ns2和刀具坐标系有关。

因此，若要得到位置偏移误差，首先要已知轴向误差。根据机床结构，工作台旋转型和刀具旋转型机床，主动轴的旋转必会带动从动轴转动，因此需先对Ns1求解再对Ns2求解。对于混合型机床，两旋转轴分布两端，主、从旋转轴的旋转可各自独立，所以对旋转轴轴向可无固定求解顺序。所以，对任意一类机床四个误差项的求解顺序相同，依次为轴向误差Ns1、Ns2、位置偏移误差。

3　误差测量原理

根据以上分析，得到对误差项的计算顺序，但是旋转轴位于机床内部，无法直接测量轴向。在空间运动学中，在绕旋转轴运动的圆周上取任意三点组成的平面，平面的法向量即为轴向，因此可通过每次保持一条旋转轴不动，另一旋转轴转动，以不同角度测量一点三次即可确定一条旋转轴轴向。因为对任意机床类型误差项的求解顺序相同，我们以刀具旋转型机床为研究对象。

3.1测量第一旋转轴轴向

假设测量Ns1时，取测量点为Q，取线性轴进给为Pi(Xi,Yi,Zi)，第一旋转轴旋转角度αi，第二旋转轴旋转角度φs2，用五元组表示三次测量的五轴进给为：(Xi,Yi,Zi,αi,φs2)，(i=1,2,3)。

(1)

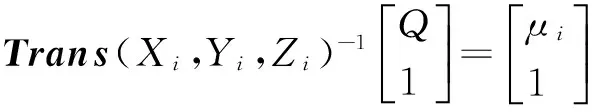
3.2测量第二旋转轴轴向

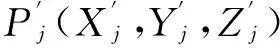
(2)

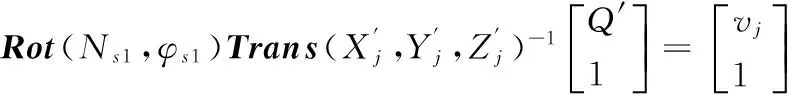
3.3计算位置偏移误差

取每次测量的任意两组五轴进给数据带入相应的表达式中，得到与Ls1s2、Ls2t有关的第一个表达式:

随着现代人生活节奏加快，生活压力不断加大，心血管疾病人群不断扩大，逐渐向低龄化方向发展，不稳定性心绞痛发病率呈逐年上升的趋势。本文将在我院治疗不稳定型心绞痛的患者作为研究对象，实践组采用复方丹参滴丸与曲美他嗪联合应用治疗。结果实践组疗效、每搏量（SV）及射血分数（EF）明显优于对照组，且差异明显有效。

(R1-R2)-1(P2-P1)=Rs2r+Rs2Ls2t+Ls1s2

(3)

其中R1、R2与α1、α2有关，Rs2与φs2有关，P1、P2与直线轴进给有关。若Q=Q′，取测量Ns1的一组数据与测量Ns2的一组数据带入相应的表达式中，得到与Ls1s2、Ls2t有关的第二个表达式

(4)

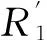
Ns1和Ns2已经由以上计算得到，所以式(3)、(4)中均只含Ls1s2、Ls2t两个未知量，联立解方程组即可求得Ls1s2、Ls2t。其他结构类型的机床也可以由同样的方式进行计算。

4　AxiSet测量方案

相较于多种测量工具，比如千分表和测试棒适用于刀具旋转型机床，对于混合型和工作台旋转型机床则不利于控制，而且是人工测量，费时且效率低。双球杆仪也可被用来测量机床误差，测量时每两轴联动，因此对多轴机床的完全测量需要多次联动。激光干涉仪[11-12]可对多轴机床快速精确的测量，只是价格高昂，而相对较便宜的AxiSetTMCheck-up组件可在三维空间内精确测量，高效省时且对三类五轴机床都适用。

AxiSetTMCheck-up组件中的测量宏程序只是对多轴机床进行快速精确的状态检查[13]，没有提供误差补偿功能，我们可以使用它的硬件设备结合误差测量原理测量机床的误差项补偿到模型中。AxiSetTMCheck-up组件中的标准球和触发式测针的实物如图4所示。

(a)标准球　　　　　　　　　(b)触发式测头

测量时标准球[13]固定于工作台上，测针安装在主轴刀具卡座上，采用以与轴平行地沿直线轨迹绕标准球运行。

4.1测量步骤

由于所有测头在使用前或者安装新的测针后都必须经过标定，且标定过程和测量过程应该使用相同的测量速度。结合测量原理，测量步骤可分为以下4步：

(1)标定测头

将主轴测头定位到标准球上方某个使测头能安全无碰撞地开始向下移动或绕行的位置[13-14]，沿与轴平行的直线轨迹测量球体表面的三个位置。如图5所示，这三个位置产生的球面位置应形成一个尽可能大的三角形，若形成的三角形过小，可能会导致计算结果不够精确。

(a)形成较大的三角形　　　　　　(b)形成的三角形过小

标定结束后，测头回到标准球中心上方，经过标定后可确定标准球的球心坐标Ob(Ob.x,Ob.y,Ob.z)。

(2)测量第一旋转轴轴向

将测针定位到参考点，第一旋转轴旋转角度αi(i=1,2,3)，保持第二旋转轴角度φs2不变，测针逼近标准球球心，线性轴进给为Pi(Xi,Yi,Zi)，测得标准球表面位置为Qi(Qi.x,Qi.y,Qi.z)。

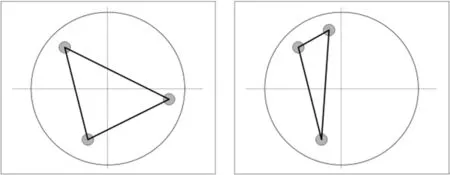
图6　C轴旋转轨迹球面坐标表示

如图6所示以CA旋转轴为例，球面坐标Qi可表示为：

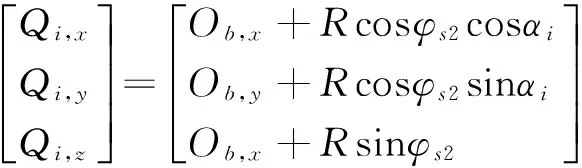
(3)测量第二旋转轴轴向

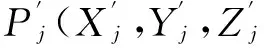
(4)旋转轴测量示意图如图7所示，将各值带入式(3)、(4)得到距离补偿矢量Ls2t和Ls1s2。

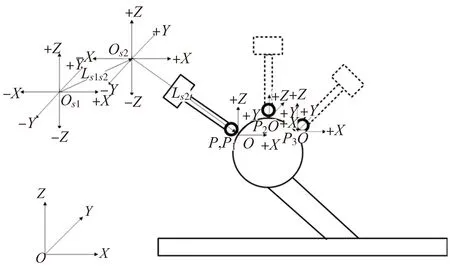
图7　AxiSet测量旋转轴示意图

4.2循环测量

若测量程序能够读取生成逼近测量点的运行方案，可实现将自动测量[14]功能集成到测量程序中，流程图如图8所示。在实际测量中可能会存在较大测量误差，使用公差验证测量结果是否在一个可接受范围内，一次测量完成后，计算机床各误差项的值，若误差err没有通过公差检验，则认为此次测量误差较大，不计入结果，重新测量，无效测量次数e超过给定值E时，停止测量并报警。为了增加精度，可循环多次测量，计算结果求平均值。

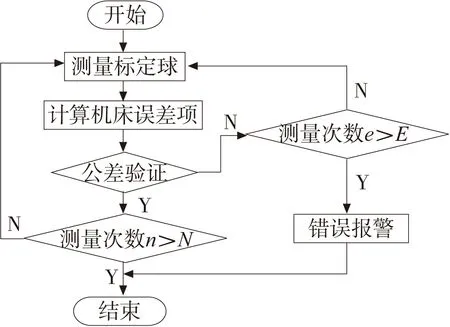
图8　循环测量流程图

循环测量可作为解决特定测量任务的通用子程序，通过参数根据具体问题加以调整。

5　实验验证

根据五轴机床运动学模型，使用C++开发一个机床模拟系统，以机床结构为CA旋转轴为例，Ns1=Z，Ns2=X，Ls1s2=20i+10j+30k，Ls2t=10i+10j-100k结构的机床为例。假设球心坐标为Ob(0,0,10)，标准球半径R=10，模拟机床运动，以不同角度逼近球心位置，通过模拟系统获取的球面位置以及相应的五轴进给，如图所示。

为了验证本文所提方法的正确性，读取测量所得数据，应用本文所提的测量方法，计算五轴机床各误差项的值。

(a)球面坐标

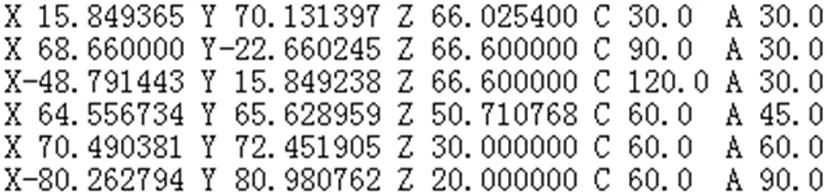
(b)刀具旋转型机床结构五轴进给

(c)工作台旋转型机床结构五轴进给

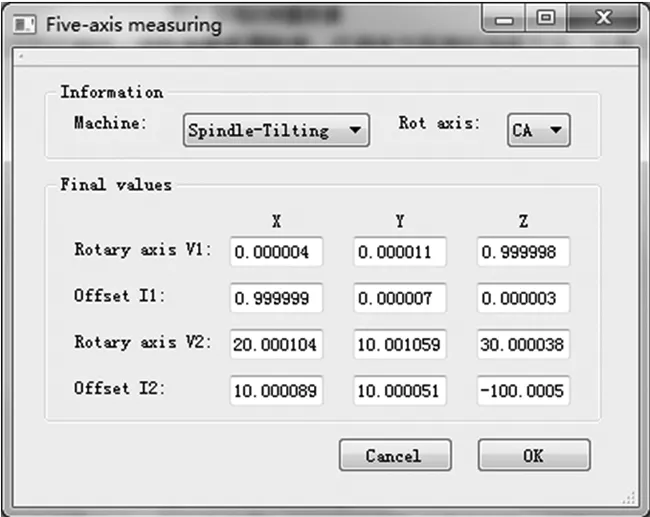
图10　计算机床误差

根据图10与机床结构的对比，说明使用本文所提测量方法得到五轴机床的各项误差参数，与预设机床结构的误差值一致且有较高的计算精度。若将测得的误差项的值补偿到机床运动学模型中，能够实现五轴机床的精确加工。

6　结论

五轴机床几何误差的精确测量对误差补偿意义重大，测量时降低人为干预确保快速准确获得测量数据，结合本文提出的测量算法，计算各轴之间的位置偏差，通过分析所得的误差项，可指导调整机床结构或者将误差项补偿到机床模型中，为五轴机床的误差诊断和补偿提供了一种快捷省时的方法。

[1] 迟关心, 郝昕宇, 张昆. 数控机床定位精度的检测及补偿[J]. 航天制造技术, 2010(3):51-54.

[2] 张为民, 杨玮玮,褚宁, 等. 五轴头回转中心的几何误差检测与补偿[J]. 制造技术与机床, 2009(2):13-15,18.

[3] W T LEI, Y Y HSU. Error measurement of five-axis CNC machines with 3D probe-ball[J]. Journal of materials processing technology, 2002, 42(10):1153-1162.

[4] IBARAKi S, IRITANI T, MATSUSHITA T. Calibration of location errors of rotary axes on five-axis machine tools by on-the-machine measurement using a touch-trigger probe[J]. International journal of machine tools and manufacture, 2012,58:44-53.

[5] 何改云, 郭龙真, 刘欣, 等. 一种双转台结构的五轴加工中心精度检测方法:中国, 201210457585[P]. 2013-02-27.

[6] 王俊雅, 齐培红. 浅谈球杆仪在数控机床中的应用[J]. 科技传播, 2011(11):75-79.

[7] DAISUKE KONO, ATUSHI MATSUBARA, IWAO YAMAJI, et al. High-precision machining by measurement and compensation of motion error[J]. International journal of machine tools and manufacture, 2008,48(10):1103-1110.

[8] Weidong Zhu, Zhigang Wang, Kazuo Yamazaki, et al. Machine tool component error extraction and error compensation by incorporating statistical analysis[J]. International journal of machine tools and manufacture, 2010,50(9):789-806.

[9] 李永桥, 陈强. 五轴数控机床通用坐标运动变换及求解方法的研究[J]. 组合机床与自动化加工技术, 2010(10):4-7.

[10] 郑飂默, 林浒, 卜霄菲, 等. 五轴机床通用运动学模型的设计[J]. 小型微型计算机系统, 2010,31(10):1965-1969.

[11] 孙克, 沈兴全. 激光干涉仪在数控机床几何误差检测与识别技术中的应用[J]. 现代制造工程, 2010(1):100-103.

[12] H.F.F.CASTRO. A method for evaluating spindle rotation errors of machine tools using a laser interferometer[J]. 2008,41(5):526-537.

[13] JJF, 1422-2013, 坐标测量球校准规范[S].

[14] Siemens AG. SINUMERIK840D sl/828D measuring cycles[EB/OL]. [2014-10-21]. http://www.automation.siemens. com/mdm/default.aspx.

(编辑李秀敏)

Rapid Measuring Method for Five-axis Machine Tool with AxiSet Device

ZHANG Na1,3,ZHENG Liao-mo2,3，YIN Zhen-yu2

(1.Chinese Academy of Sciences, Beijing 100049, China;2.Shenyang Golding NC Tech. Co., Ltd., Shenyang 110168, China)

Influenced by assembly precision and rotating parts, five-axis machine tool structural error is appeared to lead offset error in cutter tip center and reduce the machining accuracy. By analyzing the impact of the errors on the knife sites, the five-axis kinematic error model is built, and multiple measuring the center of the ball at different angles used by 3D probe - ball device, which is a part of AxiSetTMCheck-up component, to accurately solve the error terms based on the corresponding five-axis machine tool feed. The measuring method used in this paper has well consistent on various error models, by five-axis motion error compensation can not only improve the existing CNC machining accuracy, but also provide a uniform measuring basis for the multi-axis machine tool in the future.

AxiSet device; five-axis machine tool; rapid measuring

1001-2265(2015)11-0047-05DOI:10.13462/j.cnki.mmtamt.2015.11.014

2015-01-05；

2015-02-03

“高档数控机床与基础制造装备”科技重大专项：数控系统功能安全技术研究(2014ZX04009031)

张娜(1990—)，女，河南永城人，中国科学院大学硕士研究生，研究方向为数控技术，(E-mail)zn9212@163.com。

TH166;TG506

A