基于模糊层次分析法的机械材料选择*

李　磊，汪永超，唐　雨，刘晓晨，叶　雷

(四川大学 制造科学与工程学院，成都　610065)



基于模糊层次分析法的机械材料选择*

李磊，汪永超，唐雨，刘晓晨，叶雷

(四川大学 制造科学与工程学院，成都610065)

机械材料的选择是机械设计中极为关键的一步，需要考虑材料的机械性能、工艺性能、经济性以及环境属性。机械材料的选择是一个多准则、多目标、多方案的决策问题，考虑到决策者决策的模糊性，提出一种基于模糊层次分析法的多目标决策问题的解决方案。以材料的机械性能、工艺性能、经济性和环境属性为指标建立机械材料选择层次模型，应用基于三角模糊数的模糊层次分析法来求取各层次指标的权重，结合模糊综合评判法对待选材料进行评价，确定最佳材料。最后，以一个汽车变速箱齿轮材料的选择为例，说明该方法的可行性与实用性。

机械材料选择；三角模糊数；模糊层次分析法；模糊综合评判法

0　引言

机械行业对国民经济的发展起着支撑作用，在经济发展中占有非常重要的位置。机械设计作为机械行业的基础，对整个机械行业的发展起着关键性作用。机械设计中，如何合理的选择机械材料是整个设计过程中非常重要的一步，直接影响所设计产品的服务性能和成本[1]。在传统的机械设计中，机械材料的选择主要依靠设计人员的经验和查阅手册进行选择。一方面设计人员的经验存在局限性；另一方面机械材料的种类繁多，性能各异，材料选择所涉及的因素多，且因素之间相互制约[2]；另外，满足选材要求的材料可能有多种，如何评价这些材料的优劣，又是一个很模糊的概念。因此，研究出一套完善的机械材料选择评价体系具有重要意义。

目前，模糊综合评价法[3-4]、灰色关联度法[5]、加权平均法[6]和TOPSIS法[7]是机械工程、经济和管理等众多领域广泛应用的多目标选择评价体系。模糊综合评价法充分考虑人在判断事物时的模糊性，用量化的具体数值来表示定性化的因素；灰色关联度法根据因素之间发展趋势的相似或相异程度来衡量因素间的关联程度；加权平均法在测定各评价指标的基础上给出相应权重，用加权平均值来综合，得到被评价对象的评价值；TOPSIS法也称逼近于理想解的排序方法，是多指标决策的一种有序方法。本文分析了上述方法的优缺点，提出了一种基于模糊层次分析法[8]的机械材料选择方法。

机械材料的选择是一个多因素、多层次、多方案的综合决策问题。模糊层次分析法是将层次分析法和模糊评判法相结合的一种理论方法。本文应用模糊层次分析法选择机械材料，该方法运用层次分析法[9-10]建立层次结构模型，利用三角模糊数[11-13]表示专家判断信息，构造相应的三角模糊数判断矩阵求得各指标权重，最后结合模糊综合评判法对各方案进行综合评判，得出最优方案。

1　三角模糊数

在实际问题中，决策者在进行相关因素的权重分析并给定评判时，给出的评价一般不可能是一个精确的实数m，而是用“在m左右”来表达。荷兰学者F.J.M.VanLaarhoven和W.Pedrycz提出了用三角模糊数表示模糊比较判断的方法，三角模糊数(l, m, u)在表达介于某个数左右的模糊评判时具有独特的优势。

定义一：给定论域R上的一个模糊集是指对任何x∈R，都有一个数μ(x)∈[0, 1]与之对应，μ(x) 称为x对R的隶属度，μ称为隶属函数。

定义二：设论域R上的模糊集M，如果M的隶属度函数uM:R→[0,1]表示为

(1)

式中l≤m≤u， l和u表示模糊的程度，u-l越大，模糊程度越高。

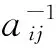
为了由三角模糊判断矩阵求出各指标的权重，以下给出几个关于三角模糊数运算法则及可能度的定义。不妨设三角模糊数aij=(lij,mij,uij),akh=(lkh,mkh,ukh)。

定义三：三角模糊数运算法则：

aij⊕akh=(lij+lkh,mij+mkh,uij+ukh)

(2)

aij⊗akh=(lij×lkh,mij×mkh,uij×ukh)

(3)

(4)

定义四：三角模糊数aij≥akh的可能度：

(5)

模糊算子∧表示取小，即a∧b=min(a,b)。

定义五：三角模糊数aij大于其他m-1个三角模糊数akj(K=1,2,…,m,k≠i)的可能度：

K(aij≥a1j,a2j,…,amj)=minK(aij≥akj)

(6)

定义六：某一指标xi的模糊判断程度：

m(xi)=ai1⊕ai2⊕…⊕ain=

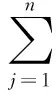
(7)

定义七：全部指标的总模糊判断程度：

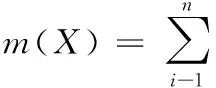
(8)

定义八：指标xi对其他指标的模糊综合程度：

Si=m(xi)⊗m(X)-1

(9)

定义九：指标xi与其他指标相比综合重要程度：

d(xi)=K(Si≥S1,…,Sn)=minK(Si≥Sk)

(10)

其中k=1,2,…,n,k≠i。

由此可得各指标的权重模糊向量：

W=(d(x1),d(x2),…,d(xn))

(11)

归一化处理后，得各指标的权重模糊集：

W′=(d(x1)′,d(x2)′,…,d(xn)′)

(12)

2　机械材料选择评价体系

2.1评价体系模型建立

随着各种选材方法的提出，机械设计中材料的选择已经由定性阶段过渡到了定量阶段。为了使所建立的评价体系运用实施方便，本文综合考虑了影响材料选择的诸多因素，最终以机械性能、工艺性能、经济性和环境属性为评价指标建立机械材料选择体系，每类指标包含相关子指标。

机械性能B1，材料在载荷作用下抵抗破坏的性能。主要包括塑性C1、耐磨性C2、疲劳强度C3、刚度C4。

工艺性能B2，材料在加工过程中对不同加工方法的适应性。主要包括铸造性能C5、锻造性能C6、焊接性能C7、切削性能C8、热处理工艺性C9。

经济性B3，材料费用约占产品成本的30%，评价材料的经济性应考虑材料的整个寿命周期。主要包括材料成本C10(材料选购或开采费用)、加工制造成本C11、回收处理成本C12。

环境属性B4，随着全球环境的不断恶化，资源、能源的匮乏，材料的环境属性越来越受到人们的重视。主要包括污染性C13、回收性C14、分解性C15、能源消耗C16。

综上所述，建立机械材料选择评价体系层次模型如图1所示。

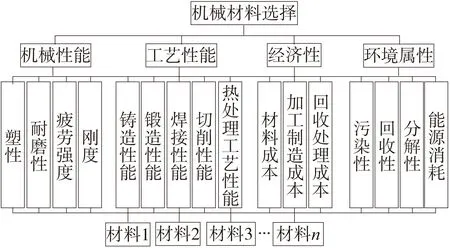
图1　机械材料选择评价体系层次模型图

2.2指标权重求解

层次模型建立后，就要求出每一层次内各指标对于上一层次相关指标的相对重要程度，即权重。确定权重的关键在于建立模糊判断矩阵。根据建立的模糊判断矩阵，可以求解出各指标的权重。

2.2.1构建三角模糊判断矩阵

根据建立的评价体系层次模型和专家评价小组评判信息，创建三角模糊判断矩阵R=(rij)n×n=(lij,mij,uij)n×n，如表1所示。

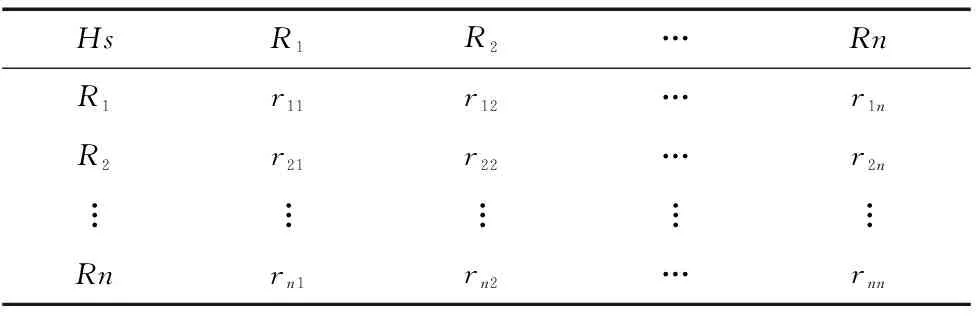
表1　三角模糊判断矩阵

其中Hs为上一层次的某一指标，R1～Rn为本层次所有指标，rij=(lij,mij,uij)为一三角模糊数，lij、mij、uij分别表示针对指标Hs而言，指标Ri相对于指标Rj重要程度的最悲观估计、最可能估计和最乐观估计。为了使rij能够实现指标间相对重要程度的定量表述，本文采用如表2所示的0.1～0.9标度法给予数量标度。

表2　0.1～0.9标度法

2.2.2层次单排序

层次单排序是指针对上一层某一指标而言，本层次所有指标的重要性排序，即计算出本层次所有指标的权重向量。不妨设n位专家评判小组成员给出的三角模糊判断矩阵集为：

其中k=1,2,…,n。

权重向量具体求解过程如下：

第一步：由公式(7)计算某指标xi的模糊判断程度m(xi)；

第二步：由公式(8)计算与指标xi同层次所有指标的总模糊判断层度m(X)；

第三步：由公式(9)计算指标xi对同层次其他指标的模糊综合程度Si；

第四步：由公式(10)计算指标xi与同层次其他指标相比的综合重要程度d(xi)，即指标xi的权重；

由上述计算可得到同层次所有指标的权重模糊向量：

W=(d(x1),d(x2),…,d(xn))

进一步归一化处理后，得到各指标的权重模糊集：

W′=(d(x1)′,d(x2)′,…,d(xn)′)

2.2.3层次总排序

为了得到同一层所有指标相对于目标层的重要性排序，必须在层次单排序的基础上进行层次总排序。层次总排序就是针对目标层而言，本层次各指标的重要性排序。

不妨设上一层的层次总排序已经完成，上一层指标A1,A2,…,Am得到的权重值分别为a1,a2,…,am；本层指标B1,B2,…,Bn针对上一层指标Aj的层次单排序权重为：

Wj=(d(B1)j,d(B2)j,…,d(Bn)j)(当Bi与Aj无关时，d(Bi)j=0)，那么本层次B的层次总排序权重为：

W=(b1,b2,…,bn)

(13)

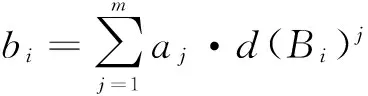
重复以上过程，可得到各层次指标关于目标层的权重向量，实现所有指标关于目标层的重要性排序。

3　模糊综合评判法

模糊综合评判法是一种基于模糊数学的综合评判方法，该方法在对某事物进行评判时综合考虑诸多因素的影响，利用模糊变换对该事物做出综合评判。

3.1基本原理

首先确定被评价对象的指标集合U={u1,u2,…,un}，评价等级集合V={v1,v2,…,vs}；然后确定各指标的权重和隶属度向量，得到模糊评判矩阵；最后将指标的权重向量和模糊评判矩阵进行模糊运算并归一化处理，得到模糊综合评判结果。

3.2多级模糊综合评判法

在进行模糊综合评判时，若评判对象的环境比较简单或影响评判对象的指标较少(一般不多于6个)，可用一级模糊综合评判。对于复杂的系统，当影响被评判对象的指标较多时则难以分配各个指标的权重，而且指标可能处于不同的层次，若用同一准则对不同层次的指标进行权重分配则会造成分配的不合理。因此，对于多层次多指标的系统应使用多级模糊综合评判法。本文对于机械材料选择的系统使用二级模糊综合评判法。

二级模糊综合评判法实施步骤：

第一步：建立指标集U={u1,u2,…,un}；子指标集ui={xi1,xi2,…,xim},(i=1,2,…,n)；评语集V={v1,v2,…,vs}。

第二步：对每个子指标集ui分别进行一级模糊综合评判。

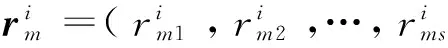
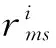
②确定子指标集ui的权重向量Wi(由第2.2.2小节求得)。

③计算一级模糊综合评判向量Bi=Wi·Ri。(其中“·”为模糊算子[14])

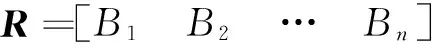
第四步：计算综合评判得分。选择评语集V=(好，较好，中等，较差，差)，并附上相应的分数V=(100，80，60，40，20)。则综合评判得分可按下式计算：

F=V·BT

(14)

得分越高的材料综合性能越好。

4　实例应用

某厂设计汽车变速箱齿轮。考虑到齿轮的主要失效形式(齿面点蚀、齿面胶合、齿面塑性变形、轮齿折断)，因此要求齿轮材料有高的弯曲疲劳强度和接触疲劳强度，齿面要有足够的硬度和耐磨性，芯部要有一定的强度和韧性。下面对满足设计要求的四种材料进行模糊层次分析法，即45#、20CrMnTi、38CrMoAl、40Cr，从中选出最佳材料。

4.1确定指标权重

由设计小组三位专家成员分别对指标层各指标进行两两比较判断，采用0.1～0.9标度法对判断结果进行数量标度，并用三角模糊数表示，如表3所示。

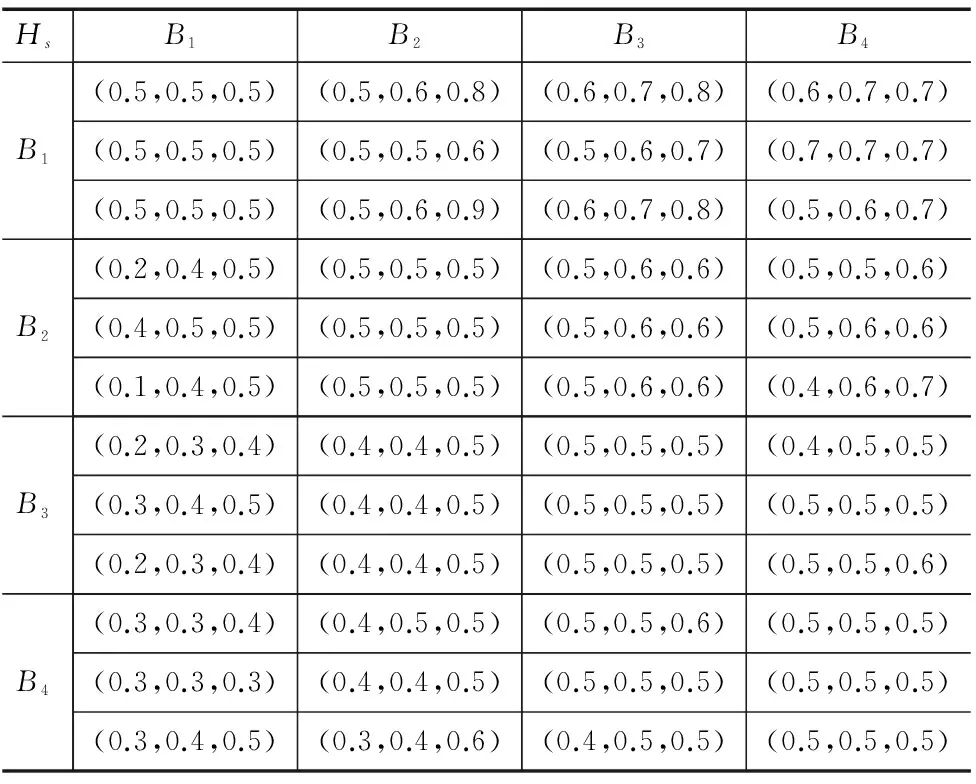
表3　指标层三角模糊数

将三位专家的判断结果进行加权平均处理后得指标层三角模糊判断矩阵，如表4所示。

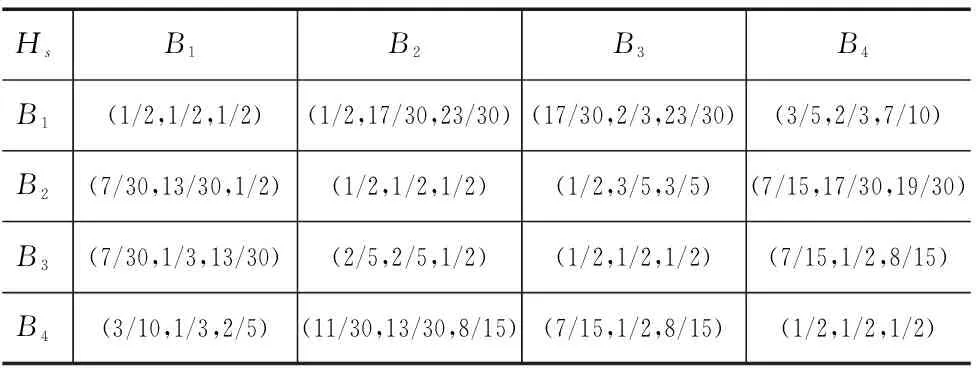
表4　指标层三角模糊判断矩阵

按2.2.2节所述，并结合公式(7)、(8)、(9)、(10)、(11)、(12)可得指标层权重向量：

W′=(0.4470,0.2924,0.1279,0.1327)

由上所述，采用相同的方法可以构建子指标层三角模糊判断矩阵，计算出子指标层权重向量，并根据公式(13)计算出层次总权重。计算结果如表5所示。

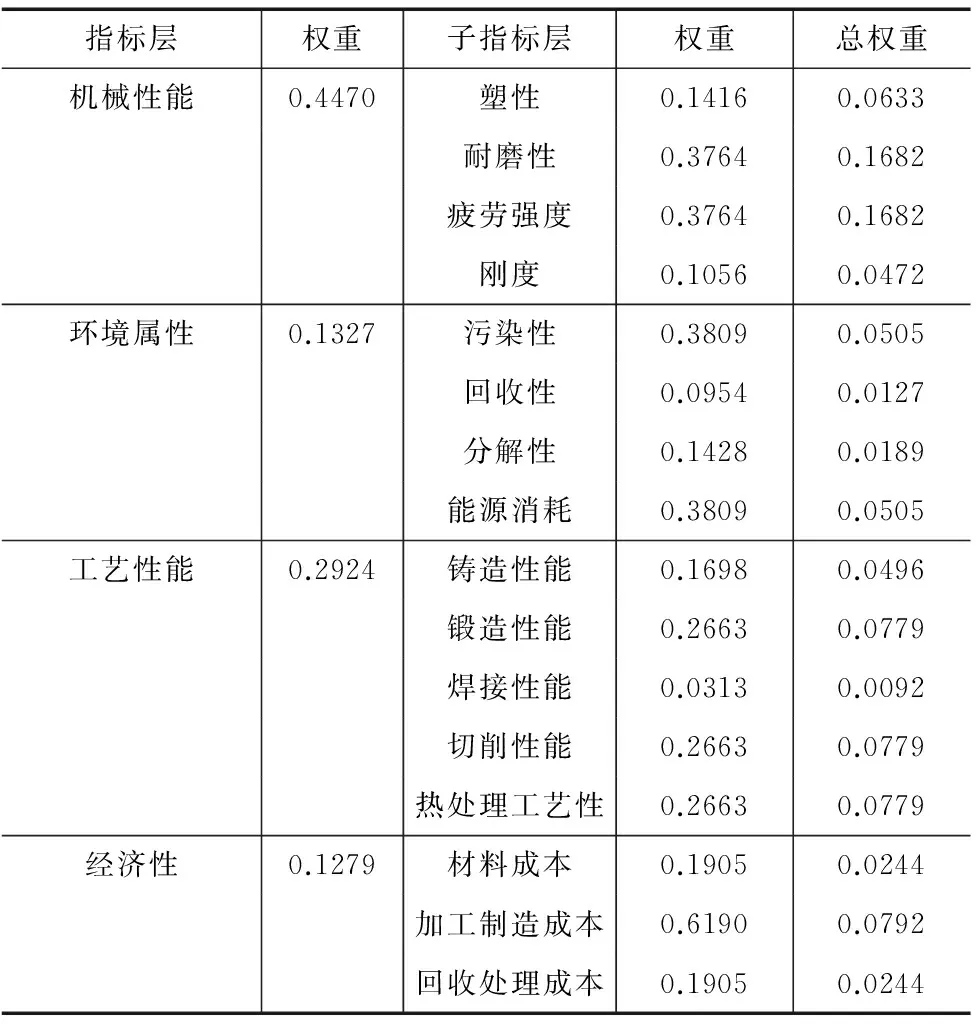
表5　各层次指标权重

4.2进行模糊评判

建立指标集U={B1,B2,B3,B4}，子指标集B1={C1,C2,C3,C4}、B2={C5,C6,C7,C8,C9}、B3={C10,C11,C12}、B4={C13,C14,C15,C16}，评语集V={好，较好，中等，较差，差}。

设计小组专家对待选材料的各个子指标集分别进行单因素评判，得到相应的隶属度矩阵如表6所示。

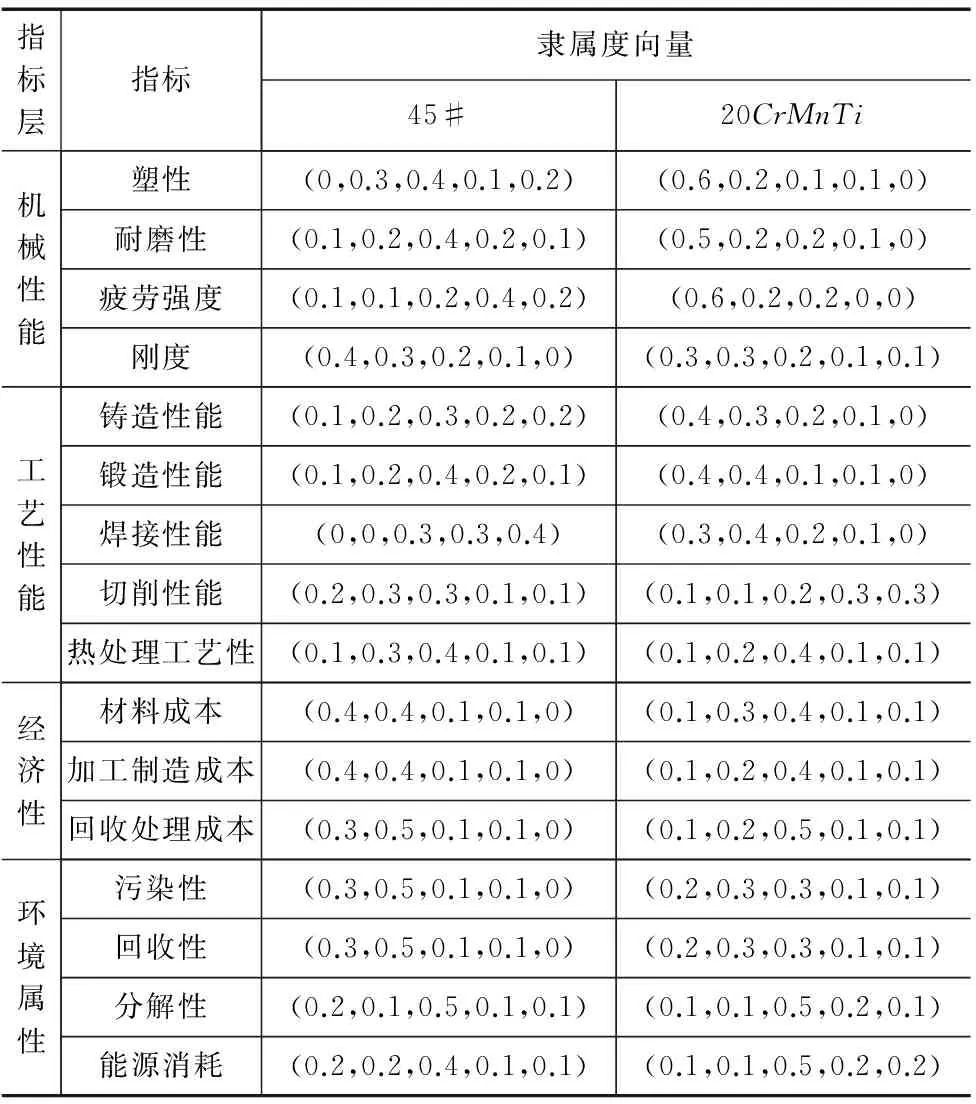
表6　待选材料隶属度矩阵

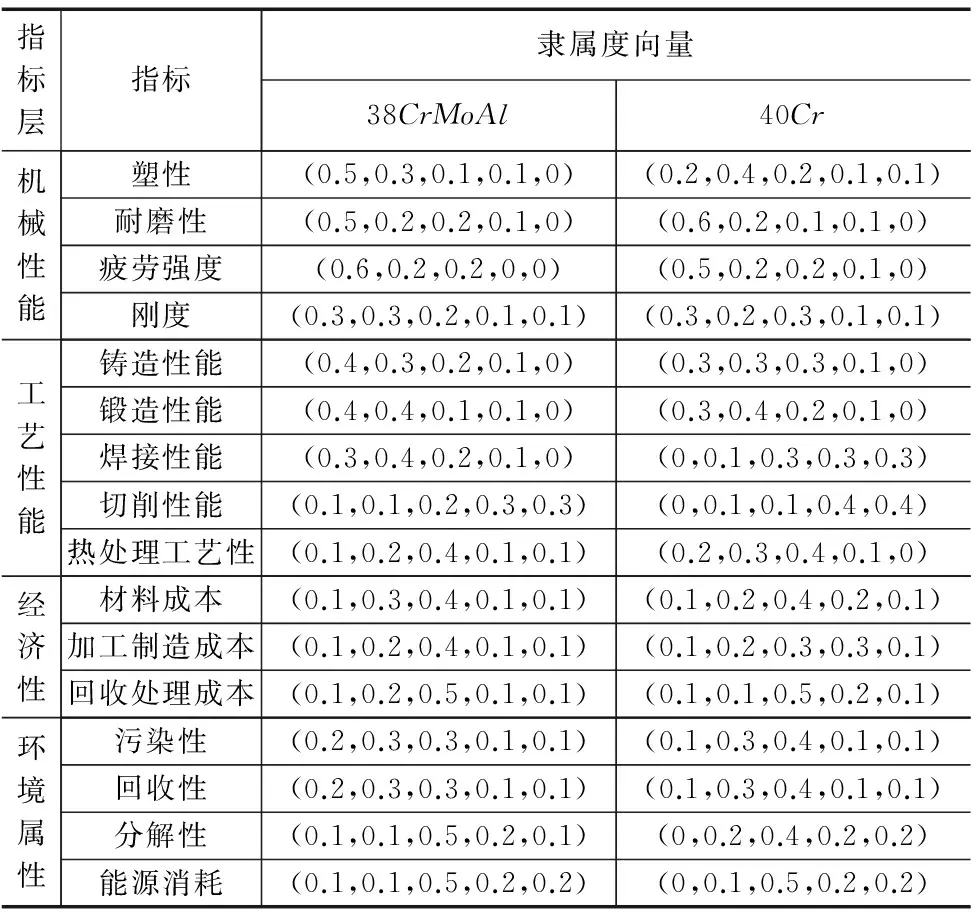
续表

下面以待选材料45#的机械性能为例，进行一级模糊综合评判。

由表5和表6可知，机械性能对应的子指标权重向量和隶属度矩阵如下：

W1=(0.1416,0.3764,0.3764,0.1056)

由此可得一级模糊综合评判向量：

B1=W1·R1=

(0.1175,0.1871,0.3036,0.2506,0.1412)

同理可求出待选材料45#的工艺性能、经济性和环境属性的一级模糊综合评判向量，如下所示：

B2=(0.1235,0.2470,0.3533,0.1499,0.1264)

B3=(0.3810,0.4191,0.1000,0.1000,0)

B4=(0.2476,0.3286,0.2714,0.1000,0.0524)

B4=(0.2476,0.3286,0.2714,0.1000,0.0524)

由计算所得的一级模糊综合评判向量，可进一步进行二级模糊综合评判。评判矩阵为：

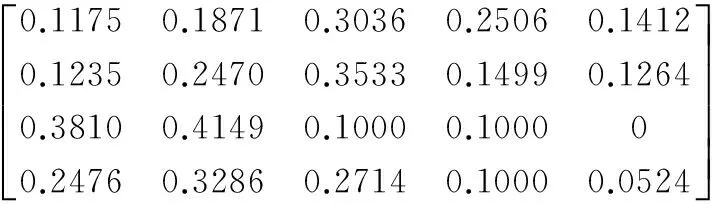
指标层权重向量：

W=W′=(0.4470,0.2924,0.1279,0.1327)

由此可得二级模糊综合评判向量：

B=W·R=(0.1702,0.2531,0.2878,0.1819,0.1070)

重复上述过程，可以得到待选材料20CrMnTi、38CrMoAl、40Cr的二级模糊综合评判向量分别为：

B1=(0.3389,0.2211,0.2566,0.1057,0.0670)

B2=(0.3171,0.2229,0.2425,0.1529,0.0697)

B3=(0.1717,0.2440,0.3631,0.1393,0.0844)

4.3计算各材料得分

由式(14)可得各待选材料得分：

45#：F=V·BT=63.9520。

20CrMnTi：F1=V·B1=72.5420。

38CrMoAl：F2=V·B2=71.6020。

40Cr：F3=V·B3=65.7360。

从各材料的得分可以看出，20CrMnTi得分最高，其次是38CrMoAl，选择得分最高的20CrMnTi为汽车变速箱齿轮材料。

5　结论

材料的选择是机械设计的重要一步，选择材料时不仅需要考虑材料的机械性能、工艺性能、经济性和环境属性，还要综合考虑选择主体在选择过程中的模糊性，因此材料的选择研究具有重大的研究意义。

文章结合模糊层次分析法和模糊综合评判法，提出了一种基于模糊层次分析法的机械材料选择方法。该方法通过三角模糊数来描述专家判断信息，利用模糊层次分析法和模糊综合评判法得到材料得分，确定最佳材料。该方法通过对设计者知识和经验的量化，减少了主观因素的影响，提高了效率，且该方法的计算过程可全部在Matlab中进行，简单快捷，具有很强的实用性。

[1] 赵忠国.机械设计中的材料的选择和应用[J].科技风,2011,9(17):58.

[2] 张红岩,郭志源.产品设计中材料选择的新思路[J].兰州工业高等专科学校学报,2001,9(3):22-26.

[3] 徐雪燕.模糊综合评价法的研究及应用[D].成都：西南石油大学，2011.

[4]SheenJN.Fuzzyevaluationofcogenerationalternativesinapetrochemicalindustry[J].ComputMathematicsAppl,2005,49(5):741-749.

[5] 孙玮玮,李雷,郑昊尧.基于灰色关联度法的大坝风险后果综合评价[J].人民黄河，2012,34(4)：102-104.

[6]WuTieeJian,SepulvedaAlfred.Theweightedaverageinformationcriterionfororderselectionintimeseriesandregressionmodels[J].StatisticsProbabilityLett,1998,29:11-29.

[7]ChenCT.ExtensionsoftheTOPSISforgroupdecisionmakingunderenvironment[J].FuzzySetsSystems,2000,114:114-121.

[8] 赵建平,汪永超,殷国富,等.基于模糊层次分析法的切削液选择[J].组合机床与自动化加工技术，2014(7):19-22.

[9] 徐俊,刘娜.层次分析法的基本思想与实际应用[J].情报探索,2008(12):113-115.

[10] 刘帅,蔡照鹏.层次分析法及其建模过程[J].福建电脑,2011,27(12):78-79.

[11] 曾祥纪,蒋惠园.基于三角模糊数的综合评价法在互通立交方案选取中的应用[J].武汉理工大学学报, 2008,32(3):543-546.

[12]DePK,ARawat.Afuzzyinventorymodelwithoutshortagesusingtriangularfuzzynumber.FuzzyInformationandEngineering,2011,3(1):59-68.

[13] 曹柬, 李平,周根贵. 基于三角模糊数和层次分析法的模型在导弹系统性能评价中的应用[J]. 兵工学报, 2005,26(4):566-569.

[14] 谢丽娟，陈俏.模糊综合评判中合成算子的选取[J].科协论坛(下半月),2012(9):103-104.

(编辑李秀敏)

Mechanical Material Selection Based on FAHP

LI Lei，WANG Yong-chao，TANG Yu，LIU Xiao-chen，YE Lei

(School of Manufacturing Science and Engineering , Sichuan University ,Chengdu 610065,China)

The choice of mechanical material is a key step in mechanical design,the mechanical performance, process performance, economic cost and environmental performance of the material should be considered. And select the optimal material among many alternatives is a multi-criteria decision-making problem. After considering the vagueness and uncertainty on judgments of the decision-makers, then putting forward a solution to solve the multi-objective decision-making problem based on fuzzy analytic hierarchy process. Establish a hierarchical model of mechanical material selection which choose mechanical performance, process performance, economic cost and environmental performance of the material as its indexes, and decided each index weight by using fuzzy analytic hierarchy process with triangle fuzzy number. The best material is the one that got the highest scores after evaluating under the method of fuzzy comprehensive evaluation. Finally, an example of mechanical material selection is given to illustrate the feasibility and practicability of the method.

mechanical material selection; triangle fuzzy number;fuzzy analytic hierarchy process;fuzzy comprehensive evaluation method

1001-2265(2015)11-0008-05DOI:10.13462/j.cnki.mmtamt.2015.11.003

2015-01-05；

2015-02-08

国家“十一五”科技支撑计划项目(2006BAC02A02)

李磊(1991—)，男，四川泸县人，四川大学硕士研究生，研究方向为机械制造及其自动化，绿色设计与制造，(E-mail)nongqililei@163.com。

TH142;TG506

A