基于ADAMS的差速AGV转弯过程仿真实验研究
2015-10-30高延峰王承洋
高延峰,王承洋
(南昌航空大学,江西 330063)
1 仿真实验目的
自动导引小车(Automatic Guided Vehicle),通常称作AGV。根据美国物流协会的定义,AGV是指“装备有电磁或光学等自动导引装置,能够沿规定的导引路径行驶,具有安全保护装置以及各种移载功能的运输车辆。”AGV已成为现代物流系统的关键设备,是工厂自动化(FA),仓储物流(AS/RS)、柔性制造系统(FMS)和计算机集成制造系统(CIMS)等先进生产方式中不可或缺的自动化设备。
本文研究的是一款差速驱动、磁条导引的AGV小车。以往的很多研究已经建立了小车基于理论力学的运动学和动力学模型,但这些研究往往是以小车导航和控制系统设计为目的的,对小车行走过程,特别是转弯过程中的动力学特性没有给予足够的关注。事实上,小车的转弯是一个十分复杂的动力学过程,它与小车的结构设计、驱动系统设计、行走路径规划、搬运载荷等都有密切的联系。所以,在小车研制阶段,充分考虑小车转弯时的动力学特性是十分必要的。然而,通常情况下,装备在研制阶段,主要采用实体样机进行行走实验和调试。这种方法耗时长、成本高,实验过程和测试结果也往往不够全面。基于虚拟样机技术的仿真实验可以很好的解决这个问题。通过AGV转弯过程仿真实验研究,可以详细了解小车转弯的动力学特性及其影响因素,并为小车的研制与调试提供理论实验数据。
2 仿真实验方案
2.1 仿真实验工况
为了更加真实地反应小车的工作环境,也为了分析方便,对仿真实验作如下设定:
AGV一般在厂房内使用,路面平坦,速度也较低,所以设定小车在水平路面上匀速行驶,忽略空气阻力;载荷设定为小车的额定载荷300公斤;为了更加完整地仿真小车的行走特性,设定小车的运动过程为先直线行走,再向右做直角转弯,最后恢复到直线行走状态。
2.2 实验方案
本仿真实验主要研究转弯半径对小车行走特性的影响,为此总体上按以下两步进行。
首先,设定载荷位于小车上顶面型心,转弯半径和行驶速度适中,观察小车的行走过程,分别测量四个万向轮和两个驱动轮与地面的接触力,和左右悬挂弹簧的弹力,分析直线和转弯过程不同的行走特性。
其次,设定载荷位于小车上顶面型心,观察小车在不同的转弯半径下的行走过程,分别测量四个万向轮和两个驱动轮与地面的接触力,和左右悬挂弹簧的弹力,分析转弯半径对小车行走特性的影响。
3 自动导引小车建模
3.1 几何模型建模
采用SolidWorks软件建立小车的几何模型。该几何模型是面向分析的,与面向设计的模型有不同的方面,因此需要注意两点。其一是要适当的简化。机械系统中的很多元素,如较小的倒角和圆角、螺纹、孔径较小的孔、螺栓等标准件,它们的存在会大大增加动力学模型的求解难度,明显降低求解速度,还有可能产生不可预知的问题,造成无法求解,但同时实际情况下,它们对机械系统的动力学性能几乎没有影响,所以,往往在建立几何模型时就将这些元素简化。其二是运用多实体建模技术。在SolidWorks中,常见的工程文件类型包括零件、装配体和工程图等。在ADAMS中,几何模型是以构件(part)为基本单元组织的。当将SolidWorks的装配体文件导入到ADAMS后,每个零件对应着一个构件。对于一些结构比较复杂的机器和机构,往往有几十甚至上百个零件组成,但具有相对运动关系的却只有很少的几个零件。这时采用多实体建模技术可以大大提高建模效率,减小发生错误的可能性。
如图1所示,小车的行走机构由8个脚轮组成,按中心对称布置。中间两个是驱动轮,通过悬挂系统与车体柔性连接,四个角各有一个万向轮,直接安装在车体上。

图1 AGV物理模型
3.2 物理模型建模
3.2.1 车轮模型
车轮模型主要包括四个万向轮和左右两个驱动轮。由于车轮与地面的接触是小车系统与外界的唯一联系,运动过程中的所有外力(不包括搬运载荷)、振动和冲击都是经过车轮和悬挂系统传递到小车车体上的,所以车轮模型对仿真实验的准确性有着极为重要的影响。这里采用接触(contact)定义车轮模型,通过设定接触刚度(Stiffness)、阻尼(Damping)、指数(Force Exponent)、切入深度(Penetration Depth)等参数,使其与真实脚轮相似。
3.2.2 悬挂系统模型
悬挂系统模型比较简单,主要包括左悬挂和右悬挂。左悬挂由并排的两个竖直方向的圆柱弹簧构成,设定弹簧刚度为12.3N/mm,自有高度90.3mm。右悬挂处理与左悬挂相同。
3.2.3 模型验证
完成物理模型后,利用model topology map命令和model verify命令,读取和验证整体模型的拓扑结构、约束、自由度等信息。
4 转弯过程仿真实验
4.1 直线与转弯对比实验
根据前文实验方案的第一步,在ADAMS软件中通过STEP函数控制左右驱动轮的转速,实现对小车运行速度的模拟,使小车直线行驶2s后,以半径800mm向右转弯90°,再直线行走2s。同时在整个仿真过程中,在小车上顶面型心处施加300kg的集中力,以模拟负载。具体函数设定如下(角度单位是弧度):
左轮转速: S T E P(t i m e,2,-1,2.5,-2.3)+STEP(time,10.1,0,10.6,1.3)
右轮转速:-1
设定仿真时间为12.6 s,目的是使小车正好完成90度的转弯,仿真步数(Steps)100步。
4.2 转弯半径对行走特性的影响实验
根据前文实验方案的第二步,采用ADAMS的优化设计技术,测试不同转弯半径下的行走特性。如图2所示,点P是小车型心在水平面内的投影,点O是转弯轨迹的原点,点N是右侧驱动轮的中心,L是驱动轮之间的轮距,本文中L=630mm。
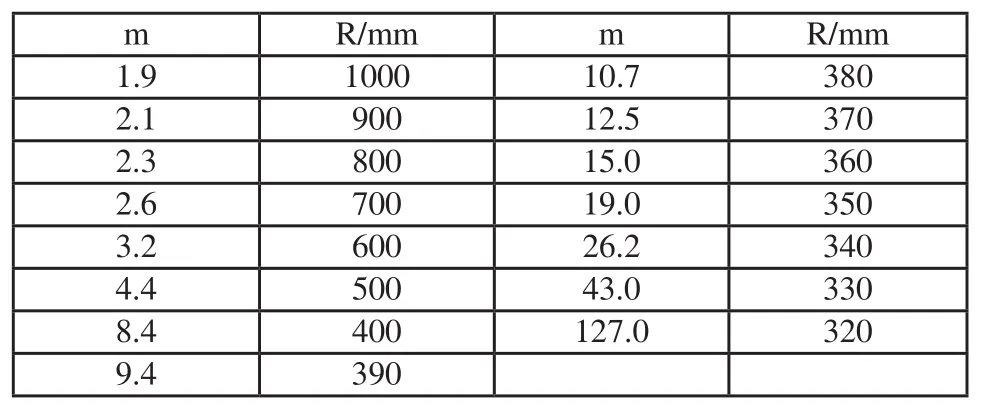
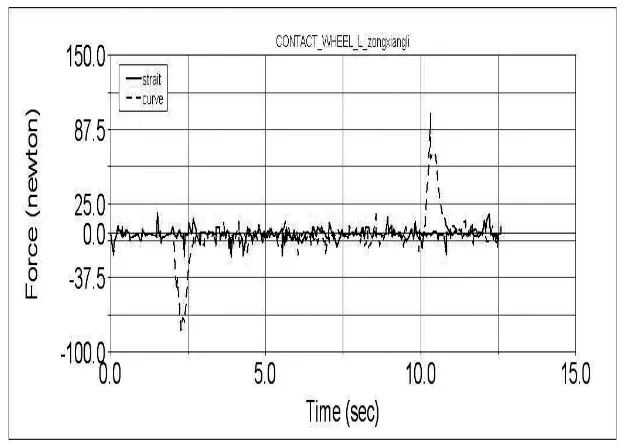
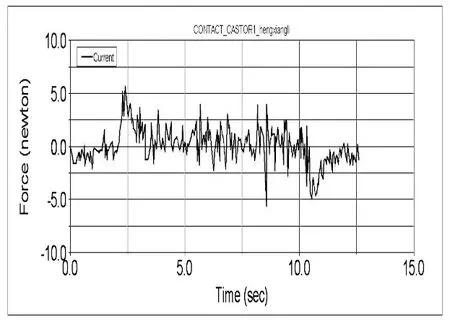
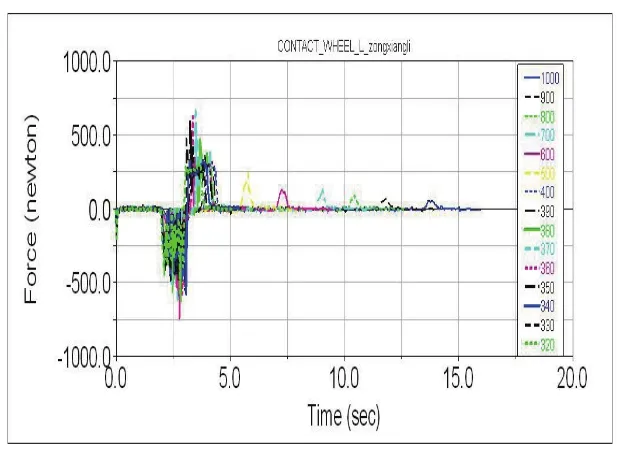
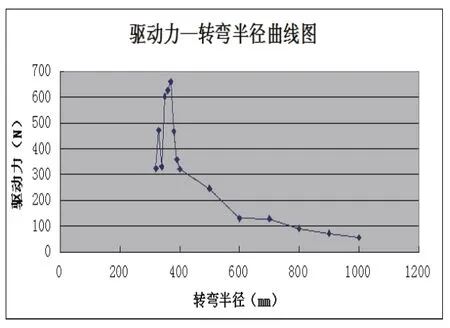
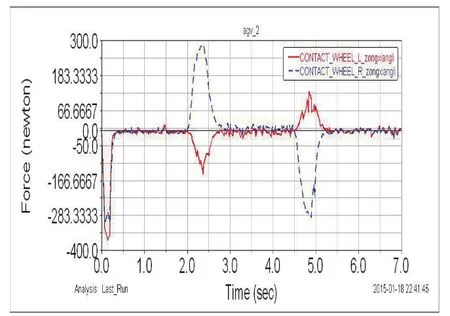
按以下三种情况分别实验:点O在点N的右侧,此时R>L/2,称为情况Ⅰ;点O在点P和点N之间,或者与P重合,此时0≤R 图2 转弯半径示意图 4.2.1 情况Ⅰ仿真实验 设定载荷位于小车上顶面型心处,并建立设计变量(Design Variable)m,含义是左驱动轮转速与右驱动轮转速之比,通过改变m的水平值控制转弯半径R,它们之间的关系是: 根据式(1)建立仿真实验数据表,如表1所示。 表1 情况Ⅰ仿真实验数据表 从表1中可以看到,设定的半径水平值并不是均匀变化的,这主要是因为转弯半径较小时,行走特性会发生明显的变化,采用更小的间隔有利于测试这一区段的特性。 为了使小车在不同半径下能够按照工况规定运动,左右驱动轮的旋转运动设定必须参数化,具体函数如下: 左驱动轮: STEP(time,2,-1, 2.5,-m)+STEP(time,2.5+9.9/(m-1),0,3+9.9/(m-1),m-1) 右驱动轮: -1 仿真时间也须参数化,设定为[5+9.9/(m-1)] s,仿真步数(Steps)100步。 4.2.2 情况Ⅱ仿真实验 此时左右驱动轮旋转方向相反,转速比m为负值。m与R的对应关系如表2所示。 表2 情况Ⅱ仿真实验数据表 为了使小车在不同半径下能够按照工况规定运动,左右驱动轮的旋转运动设定必须参数化,具体函数如下: 左驱动轮: STEP(time,2,-1,2.5,m)+STEP(time,2.5+9.9/(-m+1),0,3+9.9/(-m+1),-1-m) 右驱动轮: STEP(time,2,-1,2.5,1)+STEP(time,2.5+9.9/(-m+1),0,3+9.9/(-m+1),-2) 仿真时间也须参数化,设定为[5+9.9/(-m+1)] s,仿真步数(Steps)100步。 4.2.3 情况Ⅲ仿真实验 此时转弯轨迹的原点正好位于右驱动轮中心处,转弯半径R=315mm,右驱动轮的转速为0。 设定左右驱动轮的旋转运动函数如下: 左驱动轮:-5 右驱动轮:STEP(time,2,-5,2.5,0)+STEP(time,,4.5,0,5,-5) 设定方针时间1.98 s,仿真步数(Steps)100步。 图3是左侧驱动轮牵引力—时间曲线图。图中实线表示小车全程匀速直线行走,虚线是按实验工况要求,完成直线—转弯—直线的行走过程。从图3中可以看出,直线行走时,牵引力保持在一个较小的值不变,但在2.5s左右入弯,和在10.6s左右出弯时,牵引力陡增至直线行走状态的10倍左右,而在它们之间的稳定转弯过程中的牵引力约是直线行走时牵引力的1到2倍。可见转弯运动对小车的驱动系统提出了更高的要求。 图4是按实验工况要求行走时,万向轮的侧向力—时间曲线图,它的变化趋势与图3中的牵引力变化趋势保持一致。转弯时万向轮所受的在旋转平面内的滚动阻力并没有明显的变化,但侧向力显著增加,特别是入弯和出弯处。这主要是因为各万向轮在入弯和出弯时存在较大的侧偏角,相应产生了侧偏力和转弯的阻力距,这也正是转弯时牵引力增加的原因。 图3 直线与转弯行走牵引力对比曲线图 图4 转弯行走万向轮侧向力曲线图 5.2.1 情况Ⅰ仿真结果分析 图5中,纵轴是左侧驱动轮牵引力,横轴表示时间。图中总共有15条曲线,分别对应于表1中的15个转弯半径。图6中的纵坐标是从图5中得到的仿真过程中牵引力的最大值(即入弯和出弯时牵引力的峰值),横坐标是转弯半径。 如图6所示,牵引力峰值随转弯半径减小,呈现出先增大后减小的趋势,并在半径等于370mm时达到最大值。这是各万向轮所受阻力与转弯离心力相互抗衡的结果。前者使牵引力增大,并在转弯半径较大时起到主要作用;后者会减轻牵引力的负担,并随着转弯半径的减小和转弯角速度的增大,它的作用越来越明显,最终使牵引力下降。 此外,当半径较大时,牵引力的增长是由缓趋急的,这与万向轮切角随转弯半径的变化相符。 图5 情况Ⅰ不同直径下牵引力曲线图 图6 情况Ⅰ牵引力峰值—转弯半径曲线图 5.2.2 情况Ⅱ仿真结果分析 如图8所示,此时与情况Ⅰ时正好相反,牵引力峰值随转弯半径增大,呈现出先增大后减小的趋势,并在半径等于260mm时达到最大值。分析其原因与情况Ⅰ原理相同。 图7 情况Ⅱ不同直径下牵引力曲线图 图8 情况Ⅱ牵引力峰值—转弯半径曲线图 5.2.3 情况Ⅲ仿真结果分析 图9是驱动轮牵引力—时间曲线图,其中实线表示左侧驱动轮,虚线表示右侧驱动轮。图10是仿真过程中右侧悬挂弹簧的弹簧力曲线图。 如图9、图10所示,当R=L/2时,右侧牵引力显著增加,约是左侧牵引力的2倍以上,且右侧悬挂弹簧的振动幅值减小,这会造成承载平台的不稳定。 图9 左右牵引力对比图 图10 右侧悬挂弹簧力曲线图 通过以上分析可知,脚轮回旋需要很大的牵引力,为了减轻牵引力,有效方法是减小脚轮切角的变化和降低施加在脚轮上的载重。从差速驱动AGV的控制上看,左右驱动轮的转速比m和转弯过程所需的牵引力有很强的联系:当m的绝对值较大时,牵引力会急剧增加。在AGV设计和路径规划时,应尽量避免在L/2附近的转弯半径。 [1] (日)安部正人.汽车的运动和操纵[M].北京:机械工业出版社,1998,10. [2] 史恩秀.轮式移动机器人的运动控制技术及定位方法研究[D].西安:西安理工大学,2006,2 [3] (美)MSC.Software.MSC.ADAMS/VIEW高级培训教程[M].北京:清华大学出版社,2004,7. [4] 蔡志兴.机器人学[M].北京:清华大学出版社,2000. [5] 张洪欣.汽车系统动力学[M].上海:同济大学出版社,1996,12.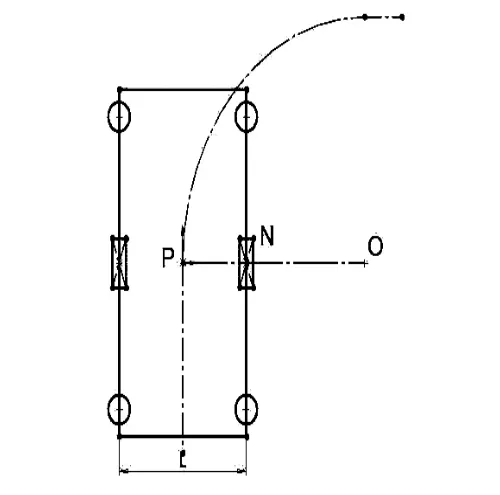


5 仿真结果分析
5.1 转弯与直线行走对比仿真实验结果分析
5.2 转弯半径对行走特性影响实验仿真结果分析



6 结论
