一种半波整流的非对称结构LLC谐振变换器
2015-10-30廖鸿飞王志强
廖鸿飞,熊 宇,王志强
(1.中山火炬职业技术学院 电子工程系,中山 528436;2.华南理工大学 电力学院,广州 510641)
0 引言
由于LLC谐振变换器的功率器件能在全负载范围内实现软开关,因此在大功率场合得到了广泛的应用。但是桥式LLC谐振变换器的输出通常采用全波整流,其功率器件数量较多,变压器副边需要中心抽头,绕制复杂,成本较高,使LLC谐振变换器在小功率场合中应用较少。
相对于全波整流,半波整流的器件数量最少,并且变压器不需要中心抽头,结构简单,可以有效的降低成本。采用半波整流的LLC谐振变换器,由于其原边谐振网络在一个开关周期中的谐振是非对称的,因此称为非对称结构LLC谐振变换器[1]。而全波整流的LLC谐振变换器称为对称结构LLC谐振变换器。
本文对非对称结构LLC谐振变换器的工作原理和参数设计进行了详细分析,并设计了120W的实验样机,对非对称结构LLC谐振变换器的参数设计及性能进行了验证。
1 非对称结构LLC谐振变换器的工作原理分析
非对称结构LLC谐振变换器的结构图如图1所示,该图中Vin为输入直流电压;开关管Q1和Q2为变换器中半桥结构的两个开关管,Q1,Q2互补导通,其占空比固定为50%。DS1和DS2分别为开关管Q1和Q2的体二极管;CS1和CS2为开关管Q1和Q2的寄生电容;Cr为串联谐振电容;Lm为励磁电感,Lr为串联谐振电感,变压器的变比为n;D为副边整流二极管,C为输出滤波电容,RL为负载。
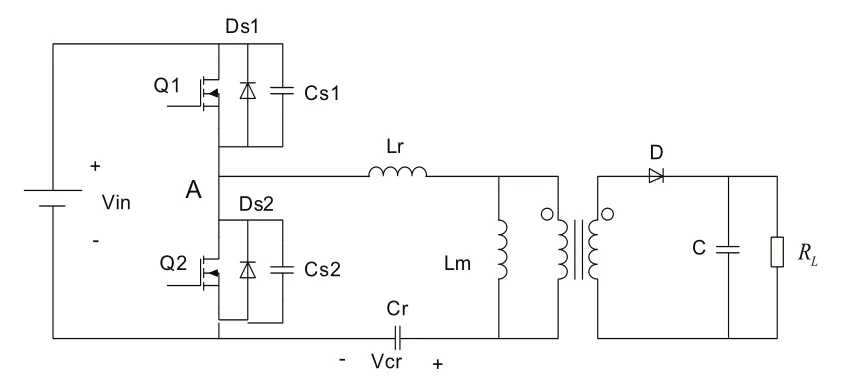
图1 非对称结构LLC谐振变换器示意图
非对称结构LLC谐振变换器的工作波形如图2所示,在一个开关周期中,非对称结构LLC谐振变换器有7个工作阶段。
阶段1(t0-t1),当t=t0时,变换器上管Q1导通,Q2断开,Q2的漏源极之间的电压为Vin;原边串联谐振电感Lr与电容Cr谐振,输出整流二极管正向导通,输入电源的能量通过变压器和输出整流二极管向输出传递。同时变压器的原边被输出电压箝位,变压器原边电压为Vp=nVo,激磁电感电流在原边电压作用下线性上升。
阶段2(t1-t2),当t=t1时,激磁电感的电流与谐振电流相等,输出整流二极管的电流下降到零,自然关断,原边激磁电感Lm不再被箝位,与谐振电感Lr,谐振电容Cr构成串联谐振。由于这个谐振比前一个谐振的周期大很多,因此电流近似为线性。
阶段3(t2-t3),当t=t2时,Q1关断,为防止Q1,Q2同时导通,Q1关断后,在Q2导通前有一定的死区时间,此时Q1,Q2均为关断状态。由于此时原边谐振电流正向流动,谐振电流给Q2的寄生电容Cs2放电,并给Q1的寄生电容Cs1充电,Q2的漏源极之间的电压下降至零。
阶段4(t3-t4),当t=t3时,由于Q2的漏源极之间的电压下降到零,Q2的体二极管DS2导通,原边电流通过Q2的体二极管继续流动,并反向增大。DS2的导通,为Q2的零电压开通创造了条件。当t=t4时,给Q2的栅极施加一个高电平,Q2实现零电压开通。
阶段5(t4-t5),当t=t4时,Q2导通,而D一直处于截止状态,因此原边激磁电感Lm, 串联谐振电感Lr和谐振电容Cr构成谐振。由于Lm较大,因此此谐振周期较长,其谐振频率远小于开关频率,谐振网络的电压超前于电流。经一段时间后,谐振电流将反向流动。
阶段6(t5-t6)当 t=t5时,Q2关断,在死区时间内,原边的谐振电流将给Q1和Q2的寄生电容充电,使A点电位上升到Vin,此时Q1的漏源极之间的电压下降到零。
阶段7(t6-t7)当t=t6时,由于Q1的漏源极之间的电压下降到零,Q1的体二极管DS1导通。当t=t7时,给Q1的栅极施加一个高电平,Q1实现零电压开通。

图2 非对称结构LLC谐振变换器的工作波形
2 参数设计
2.1 输出负载特性
由于谐振变换器的特性对负载存在一定的依赖性,因此在对LLC谐振变换器进行参数设计时,需要对副边整流电路进行等效分析,获得其交流等效电阻。由于非对称结构LLC谐振变换器的输出采用半波整流,输出整流二极管只在半个周期内导通,因此与传统的LLC谐振变换器的交流等效负载不同。
LLC谐振变换器的变压器输出为电流源性质,其电流波形近似为正弦波。输出电流平均值IO与整流网络输入电流有效值Iinrms之间的关系为:

假设此整流二端网络的输入电阻为Ri,忽略二极管的损耗,由功率平衡:
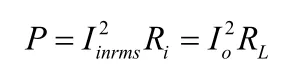
折算到变压器原边可以得到等效交流电阻为:
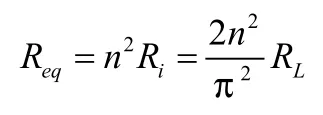
从上式可以看出,在相同负载情况下,半波整流电路的等效电阻小于全波整流电路的等效电阻[2]。
2.2 增益特性分析
由变换器的工作原理分析得到,变换器在Q1导通期间向负载传递能量,Q2导通期间原边谐振主要是为了使Q1实现软开关。因此在Q1导通期间,谐振网络的等效模型如图3所示。VinFHA为开关网络提供的方波的基波分量,Vp为输出电压通过变压器折射到原边的电压。

图3 谐振网络的等效模型
谐振网络的交流增益为[3]:
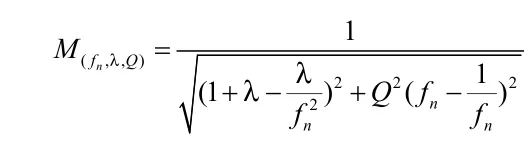
从以上分析可以看出,非对称结构LLC谐振变换器在向负载输出能量时发生谐振,其谐振特性与对称结构的LLC谐振变换器非常接近。但是由于半波整流的负载交流等效电阻小于全波整流的交流等效电阻,因此在相同参数条件下,非对称结构的LLC的Q值大于对称结构的LLC的Q值,非对称结构LLC的曲线更为平缓,这意味着在负载发生变化时,工作频率的变化范围相对较宽。图4所示为相同参数条件下非对称结构与对称结构LLC谐振变换器的增益曲线对比。


图4 两种结构LLC谐振变换器的增益曲线
2.3 软开关条件分析
LLC谐振变换器实现ZVS的条件,是谐振网络工作在感性区域,电压超前于电流。由于非对称结构LLC在不同开关模态下,谐振网络的结构不同,因此有必要对其ZVS条件进行分析。
当Q1导通、Q2关断时,其谐振网络的输入阻抗为:

当Q1关断、Q2导通时,其谐振网络的输入阻抗为:

要使谐振网络工作于感性区域,需要两种状态下的阻抗角均大于零。因此可得到实现ZVS的最大Q值为,其中Mmax为所需的最大交流增益。
同时,从原理分析中可知,在死区时间内,激磁电流需要给寄生电容放电,使MOSFET实现ZVS,因此有:

因此可得:
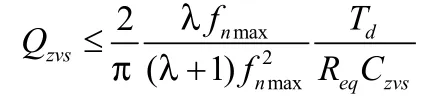
式中,fnmax为最高归一化频率,Td为死区时间,Czvs为MOSFET的寄生结电容。
设计时,为了保证实现软开关,所取Q值应小于Qmax以及Qzvs。
2.4 电流应力分析
对于非对称结构的LLC谐振变换器,输出整流二极管只在Q1导通的半个周期内导通,进行能量传递,原副边电流应力均大于对称结构的LLC谐振变换器。在Q1导通期间,原边电流包含输出的电流及激磁电流,其有效值为[4]:

由式(1)可见,非对称结构LLC变换器的输入阻抗与对称结构LLC变换器基本接近,因此两种结构的LLC变换器原边电流也基本接近。
输出整流二极管电流为原边谐振电流与激磁电流之差,而原边谐振电流ir(t)与原边激磁电流im(t)为:

因此输出整流二极管电流为:

其中ω为谐振角频率,φ为谐振网络电压与电流的相位差。
从式(2)可以看到,输出整流二极管电流并非纯正弦波,其平均电流为负载电流,因此输出整流二极管的峰值电流大小取决于其导通时间的长短,而输出整流二极管的导通时间为原边谐振电流和励磁电流相等的时刻。与相同负载下的对称结构LLC谐振变换器相比较,由于非对称结构LLC谐振变换器原边谐振电流增大,而原边激磁电流的斜率相同,因此非对称结构LLC谐振变换器输出整流二极管的导通时间增长,其峰值电流得到有效控制。图5为两种结构LLC谐振变换器的仿真波形图,从仿真波形中可见,非对称结构LLC谐振变换器的输出整流二极管的峰值电流为对称结构LLC谐振变换器输出整流二极管峰值电流的1.6倍。

图5 对称结构LLC谐振变换器与非对称结构LLC谐振变换器仿真波形对比
3 实验验证
为验证该方案的可行性,根据上述的参数设计方法,设计了120W的验证电路,输入电压为Vin=390Vdc,输出电压为Vo=24V,输出电流为Io=5A, Lr=105μ H,Lm=750μ H,Cr=22nF,变压器采用PQ32/30磁芯,采用L6599为控制芯片。
图6为Q2的驱动波形Vgs及漏源极之间的波形Vds,Q1,Q2之间留有一定的死区时间。从波形中可见,Q2导通前,其DS电压已经下降到零,Q1,Q2均实现了ZVS。图7为输出整流二极管电流id与电压波形Vd,从图中可见,输出整流二极管关断前电流已经下降到零,输出整流二极管实现了ZCS。

图6 Q2驱动波形及DS波形
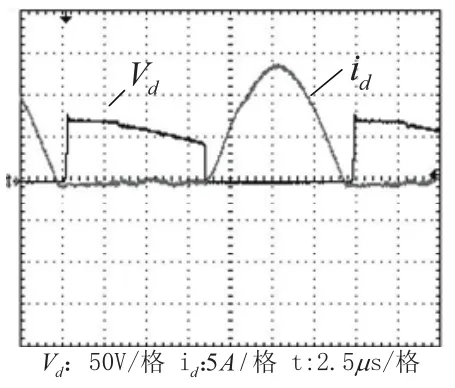
图7 输出整流二极管电压与电流波形
4 结论
针对全波整流的LLC谐振变换器输出整流功率器件较多,变压器结构复杂等缺点,本文对采用半波整流的非对称结构LLC谐振变换器进行了研究,分析了其工作原理和参数设计方法,仿真研究和实验数据表明,该方案是切实可行的,非对称结构LLC谐振变换器所有器件均能实现软开关,结构简单。该方案的提出,对LLC谐振变换器在小功率场合的应用具有重要意义。
[1] 顾亦磊,等.非对称结构多路输出LLC谐振型变换器[J].中国电机工程学报,2006,26(5):82-87.
[2] R.L.Steigerwald,A Comparison of Half-Bridge Resonant Converter[J].IEEE Transaction on power electronics 1988,3(2):174-182.
[3] James F L,Robert M.Steady-state analysis of the LLC series resonant converter[A].Proceedings of Annual Applied Power Electronics Conference,California[C],US,2001.
[4] 马皓,等.一种改进的LLC变换器谐振网络参数设计方法[J].中国电机工程学报,2008,28(23):6-11.
[5] Junseok Cho,Joonggi Kwon, Sangyoung Han.Asymmetrical ZVS PWM Flyback Converter with Synchronous Recti fi cation for Ink-Jet Printer[J].Power Electronics Specialists Conference[C].2006,1-7 .
[6] 李伟平,等.基于LLC的计算机电源设计[J].电力电子技术,2014.48(11):31-33.
