基于驾驶性能优化的混合动力车辆动态控制策略研究

张东好　项昌乐,2　韩立金,2　郑海亮

1.北京理工大学，北京，100081　　2.车辆传动国家重点实验室，北京，100081

基于驾驶性能优化的混合动力车辆动态控制策略研究

张东好1项昌乐1,2韩立金1,2郑海亮1

1.北京理工大学，北京，1000812.车辆传动国家重点实验室，北京，100081

针对混合动力车辆在动态过程中的最优控制问题，提出了一种基于驾驶性能优化的动态控制策略。根据功率分流混合动力系统的结构特点，建立了面向控制问题的功率流动态分配模型。根据驾驶员的期望状态与车辆的实际状态，提出了驾驶性能的指标函数。阐述了优先满足驾驶性能的综合控制策略，在优化模型中充分考虑了各部件的动态响应特性和发动机的转速跟踪要求，并且提出了驾驶性能实时优化算法。仿真结果表明，与传统的优化策略相比，该控制策略在不牺牲燃油经济性的同时显著提升了驾驶性能。

混合动力车辆；控制策略；驾驶性能；动态优化

0　引言

功率分流混合动力车辆兼具串联式和并联式结构的优点[1]，它利用电力和机械两路功率流传递发动机的动力，不仅可以有效地改善燃油经济性和排放性能，还能够显著地提高车辆的驾驶性能。

控制策略是混合动力车辆的核心技术，主要有基于规则的和基于优化的两种类型[2]。基于优化的方法能够得到最优或近似最优的控制效果，已经成为当前的研究热点[3-4]。然而，现有的优化策略主要以提高燃油经济性和排放性能为目标，很少考虑车辆的驾驶性能。文献[5]考虑了发动机启停和换挡过程对驾驶性能的影响，并且通过引入惩罚函数来保证车辆的驾驶性能。文献[6]系统地介绍了车辆在起步、加速、巡航、制动、转向、换挡等行驶环境中的驾驶性能，并且重点研究了加减速过程对驾驶性能的影响。文献[7]介绍了驾驶性能的控制问题，并且提出了一种兼顾驾驶性能和燃油经济性的综合控制策略。在国内，张俊智等[8]主要从冲击度的角度研究了混合动力车辆在起步、驱动状态切换、换挡和制动等典型过程中的驾驶性能。卢京民[9]也阐述了新能源车辆的驾驶性能及其评价方法等。

本文重点研究混合动力车辆在动态过程中的控制问题，并且在现有研究成果的基础上提出了一种优先满足驾驶性能的动态控制策略。它主要解决了车辆加减速过程的动力分配问题，兼顾了发动机目标转速的跟踪，实现了动态过程中的最优控制。

1　混合动力车辆数学模型

1.1功率分流混合动力系统

本文以一款双模式功率分流混合动力车辆为研究对象，其动力传动系统结构简图见图1。

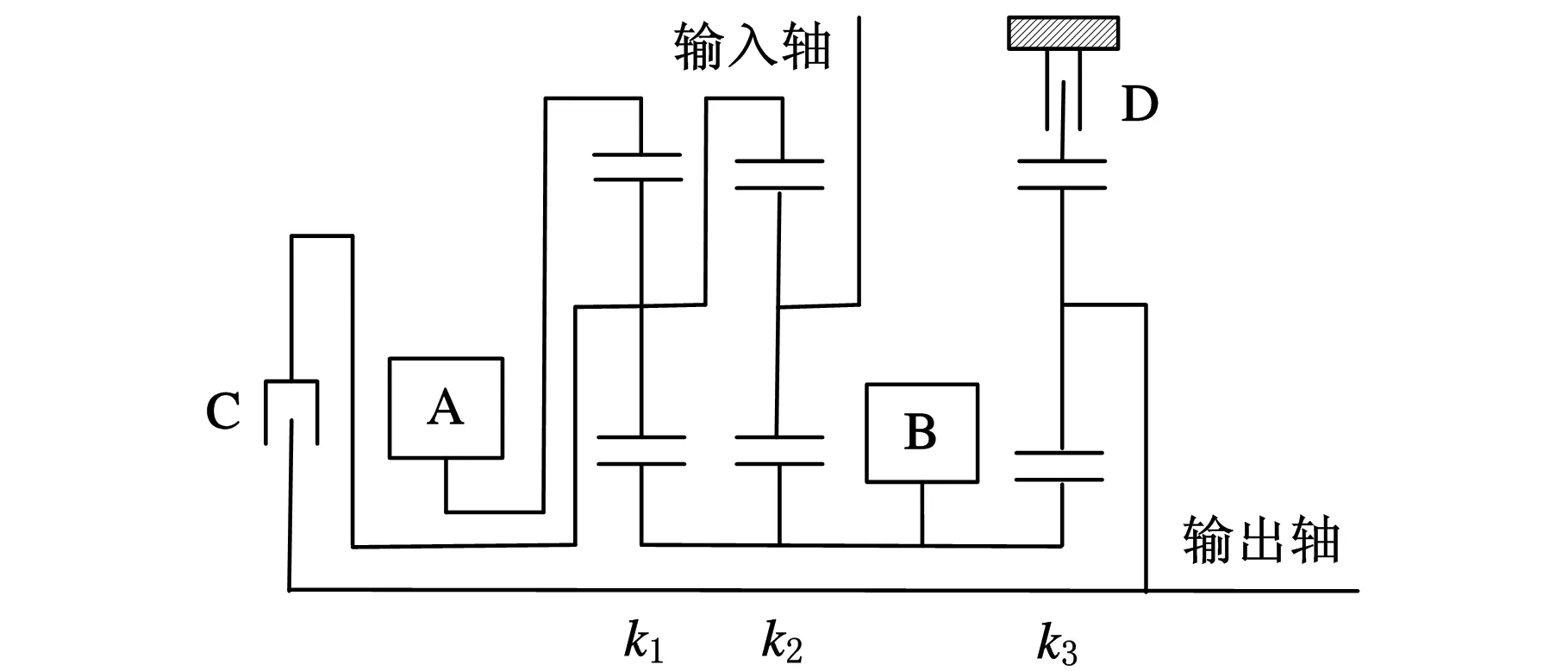
图1　双模式功率分流混合动力系统

发动机通过前传动箱与图1中的输入轴相连，输出轴通过后传动箱与车轮相连。电机A和电机B具有四象限工作能力，既可以处于发电状态，也可以处于电动状态(根据控制需要)。如果离合器C分离、制动器D结合，则系统处于电力无极变速1(EVT1)模式，主要用于车速较低的阶段；如果离合器C结合、制动器D分离，则系统处于EVT2模式，主要用于中高车速阶段。与单模式结构相比，双模式结构能够在保证动力性能的同时，成倍地扩展输出转速(车速)的范围，非常适用于重型车辆。

1.2功率流动态分配模型

对图1中的混合动力系统，将转动惯量等效到4个端口(输入轴、输出轴、电机A和电机B)，建立其动力学方程如下：

(1)

式中，TA、TB、TI、TO分别为电机A、电机B、输入轴和输出轴的转矩；JA、JB、JI、JO分别为对应部件上的等效转动惯量；ωA、ωB、ωI、ωO分别为对应部件的角速度；c11、c12、c21、c22分别为动力学耦合系数，取决于行星排的连接形式和特性参数。

对于发动机和整车，建立其动力学方程如下：

(2)

(3)

式中，Te为发动机的输出转矩；ωe为发动机的角速度；Je为发动机的转动惯量；if为前传动比；ηf为前传动效率；m为整车质量；v为车速；Tbr为制动器转矩；Fv为车辆行驶阻力，包括滚动阻力、空气阻力等；rw为车轮有效半径；ir为后传动比；ηr为后传动效率。

各部件的速度耦合方程如下：

(4)

(5)

式中，e11、e12、e21、e22为速度耦合系数。

行星排特性参数(k1、k2、k3)、传动比和传动效率、质量、转动惯量等为系统参数，各参数取值分别如下：k1=2.13，k2=2.13，k3=2.33，if=0.7，ir=4.4，ηf=0.92，ηr=0.94，rw=0.318，m=7912，Je=0.40，JI=0.36，JA=0.51，JB=1.02，JO1=0.71，JO2=0.89。其中，转动惯量由Pro/E三维建模得到，EVT1、EVT2两种模式下输出轴的转动惯量不同，分别为JO1和JO2。

根据行星排参数，可以计算出耦合系数。对于EVT1模式有：c11=-0.46，c12=0，c21=-0.54，c22=0.30，e11=2.16，e12=-3.86，e21=0，e22=3.33。对于EVT2模式有：c11=-0.46，c12=0.68，c21=-0.54，c22=0.32，e11=-1.47，e12=2.47，e21=3.13，e22=-2.13。

各部件的功率是其速度和转矩(力)的函数，表达式如下：

(6)

式中，Pe、PA、PB、Pbr、Pv分别为发动机、电机A、电机B、制动器和车辆行驶的功率。

定义输出轴与输入轴的速比如下：

(7)

联立式(1)～式(7)，并且代入系统参数，可得EVT1模式下的功率为

(8)

0.69PB-0.74(Pv+Pbr)

(9)

EVT2模式下的功率为

(10)

(11)

其中，PJe、PJv分别表示发动机和车辆在加减速过程中的功率，与其转动惯量或质量有关，这里称之为惯性功率，表达式如下：

(12)

在式(8)和式(10)中，惯性功率PJe代表了发动机的调速性能。如果PJe=0，则发动机转速稳定；如果PJe>0，则发动机加速，PJe越大加速越快；如果PJe<0，则发动机减速，PJe越小减速越快。

在式(9)和式(11)中，惯性功率PJv代表了车辆的加减速性能。如果PJv=0，车辆匀速行驶；如果PJv>0，车辆加速行驶，PJv越大加速越快；如果PJv<0，车辆减速行驶，PJv越小则减速越快。

由于功率分流混合动力系统具有两个运动学自由度，因此发动机的调速和车辆的加减速过程可以独立进行，而且两者共同决定了其他部件的运动状态。可见，惯性功率PJe和PJv体现了整个混合动力系统的动态特性，故称之为动态特性参数。

2　驾驶性能优化控制策略

2.1驾驶性能指标

驾驶性能包括了车辆操控、动力、舒适、安全等多个方面的性能，本文重点研究车辆加减速过程中的驾驶性能，它主要体现在驾驶员通过踏板开度对车辆的操控能力。驾驶员的踏板开度可以解释成车轮上的需求功率，而实际功率与需求功率的差值越小，车辆的实际状态越接近驾驶员的期望状态，车辆的驾驶性能越好。因此，驾驶性能指标如下：

LD(t)=|Pα(t)-Pd(t)|

(13)

式中，LD为驾驶性能的指标函数；Pα为驾驶员的需求功率，取决于踏板的开度；Pd为车轮上的实际功率，取决于车辆的实时运行状态以及发动机、两个电机和制动器的功率。

驾驶员的踏板包括加速踏板和制动踏板，两者的状态可以用统一的变量α来表示。α=0表示加速踏板和制动踏板都处于初始位置；α>0表示驾驶员踩下加速踏板，其数值代表加速踏板的开度，最大值为1；α<0表示驾驶员踩下制动踏板，其数值代表制动踏板的开度，最小值为-1。

驾驶员的需求功率如下：

(14)

式中，Pdmax为车轮上的最大驱动功率;Fbmax为车轮上的最大制动力。

发动机和动力电池组可以同时提供动力来驱动车辆行驶，则有

Pdmax=Pemaxηed+Pbmaxηbd

(15)

式中，Pemax、Pbmax分别为发动机和动力电池组的最大输出功率;ηed、ηbd分别为发动机和动力电池组到车轮的能量传递效率。

车轮上的实际功率包括行驶阻力功率和车辆的惯性功率，表达式如下：

(16)

把式(14)和式(16)代入式(13)，可得

LD=|fα(α)-(Pv+PJv)|

(17)

可见，驾驶性能指标LD是踏板开度α、行驶阻力功率Pv和惯性功率PJv的函数。

把惯性功率的计算式(9)和式(11)分别代入式(17)，可得EVT1模式的驾驶性能指标为

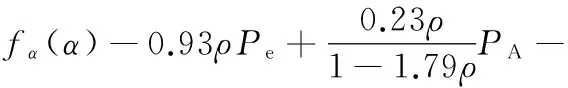
0.69PB-0.26Pv+0.74Pbr|

(18)

EVT2模式的驾驶性能指标为

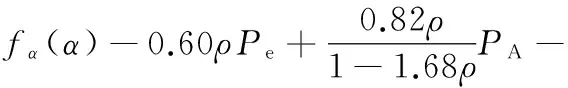
(19)

驾驶员的踏板开度、各部件的转速和车速等可以由传感器采集得到，车辆的行驶阻力可以由行驶状态计算得到，根据这些信息就可以计算出驾驶员的需求功率fα(α)、速比ρ和行驶功率Pv。因此，车辆的驾驶性能取决于发动机的功率Pe、两个电机的功率PA、PB以及制动器的功率Pbr。

2.2综合控制策略

车辆稳定运行过程中，通常有LD=0，因此不存在驾驶性能的优化问题。但是，车辆加减速过程中，或是一些恶劣工况下，受制于各部件自身的动态响应约束及其相互耦合约束，系统的功率能力短时间发挥不出来，这时就需要以驾驶性能为目标进行优化，从而最大程度上满足驾驶员的需求。

图2给出了综合控制策略的基本流程。首先，根据驾驶员的踏板开度，确定其需求功率；同时，根据车辆的实时运行状态和底层的控制算法，确定各部件的功率范围。然后，进行驾驶性能计算，并判断是否满足驾驶性能要求。如果能够满足要求，即LD=0有可行解，则在此基础上进行燃油经济性优化；如果不能满足驾驶性能要求，即LD=0没有可行解，则进行驾驶性能优化。最后，根据优化的结果，利用底层的控制算法得到实时的控制变量，并且施加到混合动力车辆。

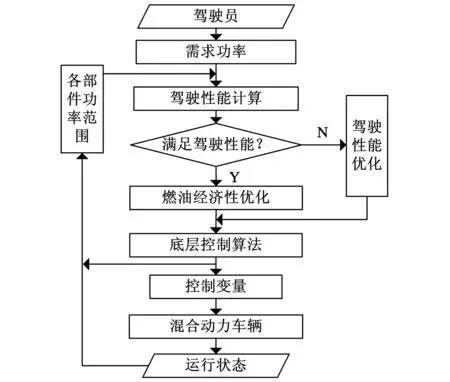
图2　控制策略流程图

可见，在上述控制策略中，优先保证了车辆的驾驶性能。由于混合动力车辆有多个自由度，故在满足驾驶性能的前提下还可以对燃油经济性进行优化，此时LD=0作为约束条件。此外，为了保证系统的稳定性，还必须对发动机的惯性功率加以约束。

2.3实时优化算法

最优化问题的模型通常由三部分组成[10]：决策变量、目标函数和约束条件。

(1)决策变量。由式(18)和式(19)可以看出，发动机的功率Pe、两个电机的功率PA、PB和制动器的功率Pbr是决定驾驶性能的主要因素，也是本文中的决策变量，表示为

u=(Pe,PA,PB,Pbr)

(2)目标函数。如果LD=0有解，则以燃油经济性为目标，表示为

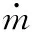
如果LD=0无解，则以驾驶性能为目标，表示为

J=minLD(Pe,PA,PB,Pbr)

(3)约束条件。约束既包括各部件自身的外特性和动态特性约束，也包括不同部件之间的相互耦合约束。外特性约束表示为

其中，动态过程中各部件的转速为已知信息，各部件的功率范围是随着其转速状态实时变化的。动态响应约束表示为

式中，ke、kA、kB、kbr分别为对应功率的允许变化率，反映了动态响应特性；Pe0、PA0、PB0、Pbr0为对应功率的初始值；Δt为动态调节的时间。

功率耦合约束表示为

式中，ηA、ηB为两个电机的机械功率与电力功率的比例，发电状态等于其效率，电动状态等于其效率的倒数；Pb为动力电池组的功率，必须满足最大充放电功率的约束。

此外，为了保证发动机的实际转速跟踪其目标转速，必须对其惯性功率加以约束。式(8)和式(10)给出了两种模式下发动机惯性功率的表达式。如果目标转速高于实际转速，则必须保证PJe>0；如果目标转速低于实际转速，则必须保证PJe<0。为了实现发动机转速的精确控制，还可以根据调速时间更加严格地限制其加速度，表示为

(20)

式中，ωecom为目标转速；δt为调速时间。

把式(20)代入式(12)，可以得到发动机的惯性功率：

(21)

通过限制发动机的惯性功率，可以实现发动机转速的精确控制，但是增加了一个等式约束条件，会使得优化空间大大减小。因此，本文在对驾驶性能进行优化时，只是限制发动机惯性功率的范围。只有完全满足了驾驶性能的条件，才能对发动机的惯性功率进行更加精确的控制。

实时优化算法的计算步骤如下：

(1)根据各部件自身的外特性约束和动态响应特性约束，确定其功率范围，并且进行离散化。

(2)根据两个电机的离散功率，利用功率耦合约束计算出动力电池组的功率，并且判断是否满足约束条件，淘汰不可行的组合。

(3)根据驾驶员的踏板开度，确定其功率需求，并且判断车辆的运行状态。如果α<0，车辆制动，此时Pe=0；如果α≥0，车辆正常行驶，此时Pbr=0。如果处于EVT1模式，则利用式(8)计算发动机的惯性功率；如果处于EVT2模式，则利用式(10)计算发动机的惯性功率。

(4)根据发动机的目标转速和实际转速，确定其惯性功率的范围，并且判断步骤(3)的结果是否满足约束条件，淘汰不可行的组合。

(5)如果α<0，则根据两个电机的功率组合，利用LD=0来计算得到制动器的功率Pbr，判断其是否满足制动器的功率约束，并且找出满足条件的变量组合；如果没有满足LD=0的组合，则对驾驶性能进行优化，即找出LD的最小值，并转到步骤(8)。

(6)如果α≥0，则根据两个电机的功率组合，利用LD=0来计算得到发动机的功率Pe，判断其是否满足发动机的功率约束，并找出满足条件的变量组合；如果没有满足LD=0的组合，则对驾驶性能进行优化，即找出LD的最小值，并转到步骤(8)。

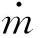
(8)根据优化的结果，利用底层控制算法得到各部件的控制变量Te、TA、TB、Tbr，并利用反馈得到的状态偏差对控制变量进行实时修正。

3　仿真与结果分析

3.1动态仿真模型

本文基于MATLAB/Simulink建立了混合动力车辆的动态仿真模型，如图3所示。

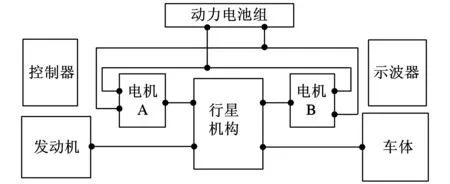
图3　混合动力车辆动态仿真模型

在发动机模型中，对本体及控制器整体建模，输入为发动机的转矩命令，输出为实际转矩，并且通过执行器作用到物理端口。在电机模型中，分别建立了机械子系统和电气子系统的模型，前者与发动机的模型相似，后者采用恒流源模型，两者通过效率模型实现功率耦合。在动力电池组模型中，采用了等效电路内阻模型，其阻值随着荷电状态实时变化。在车体模型中，利用纵向动力学方程计算出实时的行驶阻力(包括滚动阻力、空气阻力和坡道阻力等)，并且通过执行器作用到车体上。

在控制器模型中，采用嵌入式MATLAB函数编写了控制算法，输入为传感器采集的状态信息、输出为各部件的控制命令。MATLAB函数可以转化成C代码并下载到单片机中，从而大大节省了控制单元的研发时间。此外，还搭建了示波器的模型，各部件的实时运行状态以及控制命令等都可以由示波器保存下来，便于数据的分析与处理。

3.2仿真结果分析

图4中实线为车辆的循环工况，包含了频繁的加减速过程。虚线为仿真得到的实际车速，基本上跟踪了循环工况的变化，这说明本文中的控制策略实现了很好的驾驶性能。

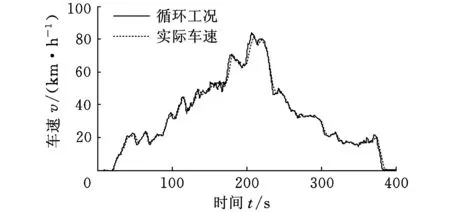
图4　循环工况跟踪效果

图5给出了发动机和两个电机的功率。可见，车辆加减速过程中，各部件功率的变化比较频繁。特别是高速阶段，由于驾驶员的需求功率未能得到满足(实际车速未能完全跟踪目标车速，见图1)，此时发动机和两个电机的功率都快速增加，从而尽量满足驾驶员的需求，以实现最好的驾驶性能。

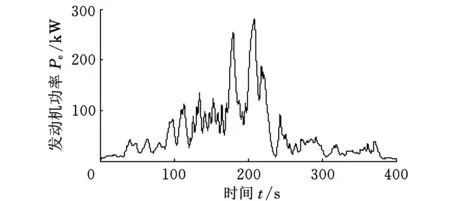
(a)发动机功率

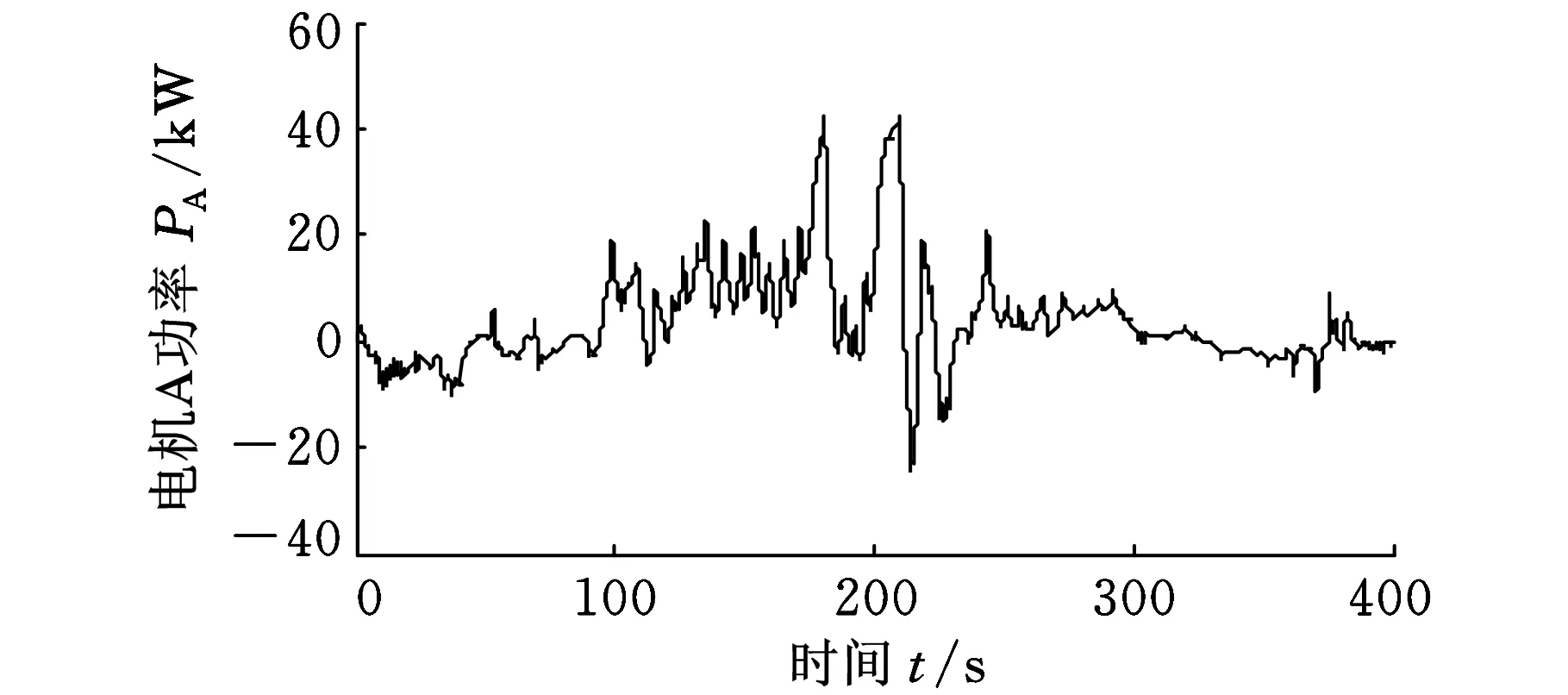
(b)电机A功率

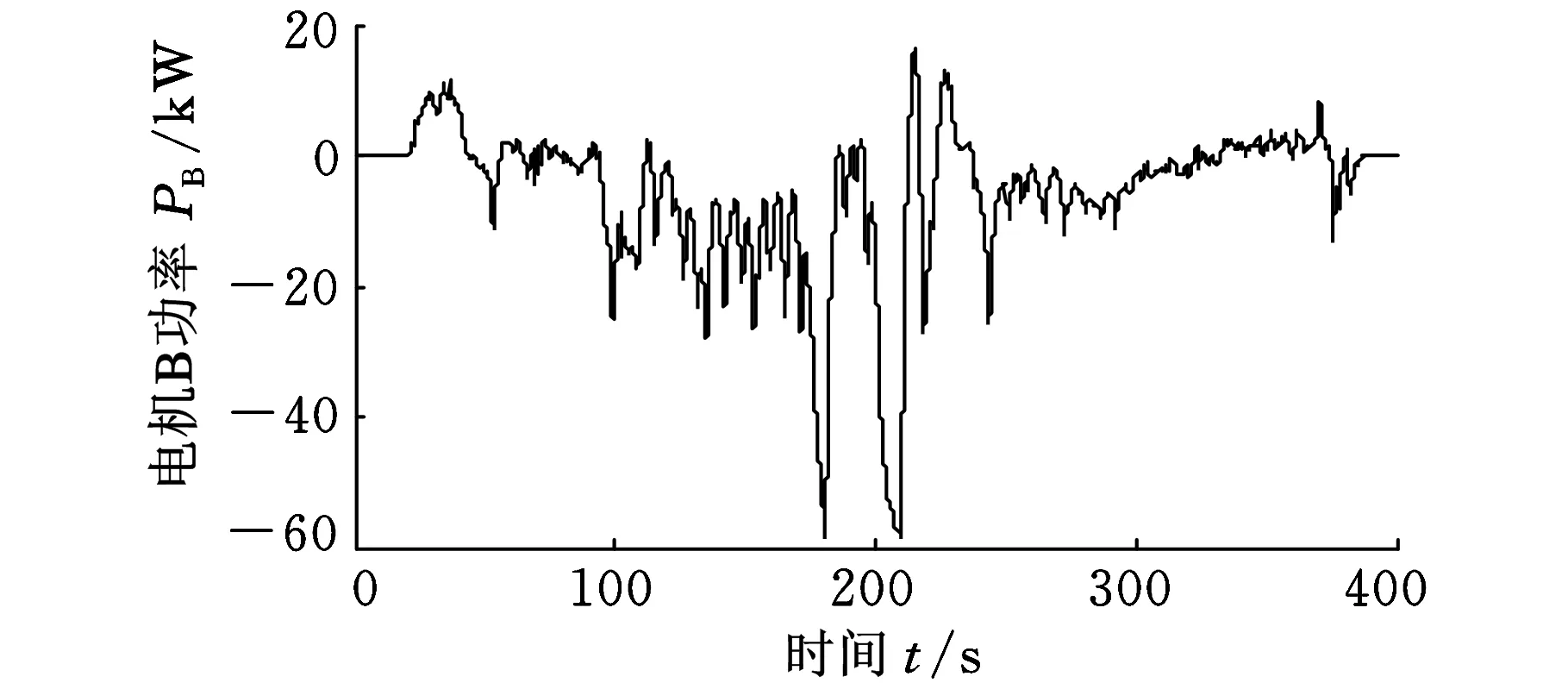
(c)电机B功率图5　各部件的功率状态

为了衡量本文中优化策略的控制效果，与单纯优化燃油经济性的传统策略进行了对比，两者的仿真平台完全相同，只是替换了MATLAB嵌入式函数中的控制算法。两种策略的对比结果见表1。

表1　不同控制策略的性能比较

可见，与传统策略相比，本文策略的油耗下降了2.6%(本文研究的重型车辆，其百公里油耗的实验数据约为29.5L)，这是由于其考虑了发动机的调速约束，从而保证了目标转速(经济性转速)的跟踪。此外，由于本文优先考虑了驾驶性能，与仅考虑燃油经济性的策略相比，其驾驶性能指标提高了32.9%。因此，本文中的驾驶性能优化控制策略能够在不牺牲燃油经济性的前提下，显著改善车辆的驾驶性能，具有很好的研究价值和应用前景。

4　结论

(1)面向动态过程建立了功率流的分配模型，提出了惯性功率的概念，发动机的惯性功率体现了调速性能，车辆的惯性功率体现了其加减速性能。

(2)提出了驾驶性能的指标函数，它代表了驾驶员的期望状态与车辆实际状态的偏差。在燃油经济性优化的基础上，提出了优先满足驾驶性能的动态控制策略，它主要解决了车辆减速过程中的最优控制问题，并且兼顾了发动机的调速性能。

(3)搭建了功率分流混合动力车辆的动态仿真模型，并利用嵌入式MATLAB函数编写了控制算法。仿真结果表明，驾驶性能优化控制策略能够在不牺牲燃油经济性的同时，显著提高驾驶性能。

(4)本文主要从理论分析和动态仿真的层面进行了研究，并且取得一些创新性成果。此外，驾驶性能还体现在换挡等状态切换过程，还需要大量的研究工作。

[1]BorhanH,VahidiA,PhillipsAM,etal.MPC-basedEnergyManagementofaPower-splitHybridElectricVehicle[J].IEEETransactionsonControlSystemsTechnology, 2012, 20(3): 593-603.

[2]WirasinghaSG,EmadiA.ClassificationandReviewofControlStrategiesforPlug-inHybridElectricVehicles[J].IEEETransactionsonVehicularTechnology, 2011, 60(1): 111-122.

[3]LiuJ,PengH.ModelingandControlofaPower-splitHybridVehicle[J].IEEETransactionsonControlSystemsTechnology, 2008, 16(6): 1242-1251.

[4]林歆悠, 薛瑞, 孙冬野. 混联式混合动力客车能量管理实时优化算法研究[J]. 中国机械工程, 2013, 24(18): 2539-2543.

LinXinyou,XueRui,SunDongye.DevelopmentofaReal-timeOptimizationAlgorithmforaSeries-parallelHybridElectricBusEnergyManagement[J].ChinaMechanicalEngineering, 2013, 24(18): 2539-2543.

[5]OpilaDF,WangX,McGeeR,etal.AnEnergyManagementControllertoOptimallyTradeoffFuelEconomyandDrivabilityforHybridVehicles[J].IEEETransactionsonControlSystemsTechnology, 2012, 20(6): 1490-1505.

[6]KoprubasiK.ModelingandControlofaHybrid-electricVehicleforDrivabilityandFuelEconomyImprovements[D].Ohio:TheOhioStateUniversity, 2008.

[7]PisuP,KoprubasiK,RizzoniG.EnergyManagementandDrivabilityControlProblemsforHybridElectricVehicles[C]//DecisionandControl, 2005and2005EuropeanControlConference.CDC-ECC’05. 44thIEEEConferenceon.Seville, 2005: 1824-1830.

[8]张俊智, 李波, 薛俊亮, 等. 混合动力电动汽车冲击度的试验[J]. 机械工程学报, 2008, 44(4): 87-91.

ZhangJunzhi,LiBo,XueJunliang,etal.ExperimentalResearchonJerkofHybridElectricVehicles[J].ChineseJournalofMechanicalEngineering, 2008, 44(4): 87-91.

[9]卢京民. 新能源汽车驾驶性研究[D]. 大连：大连理工大学, 2013.

[10]谢政, 李建平, 陈挚. 非线性最优化理论与方法[M]. 北京：高等教育出版社, 2010.

(编辑袁兴玲)

Research on Dynamic Control Strategy of a HEV Based on Drivability Optimization

Zhang Donghao1Xiang Changle1,2Han Lijin1,2Zheng Hailiang1

1.Beijing Institute of Technology,Beijing,100081 2.National Key Lab of Vehicular Transmission,Beijing,100081

To solve the optimal control problem of HEVs during the dynamic process, a dynamic control strategy was proposed based on drivability optimization. A control-oriented dynamic power distribution model was established according to the characteristics of the power-split hybrid electric system. Based on the driver’s expected status and the vehicle’s actual status, the index function of the drivability was come up with. A control strategy satisfying the drivability was presented firstly. The dynamic characteristics of the different components and the speed tracing requirements of the engine were fully considered in the optimization model. Additionally, a real-time optimization algorithm of the drivability was proposed. It can be seen from the simulation results that this control method improves the drivability dramatically without scarifying the fuel economy.

hybrid electric vehicle (HEV); control strategy; drivability; dynamic optimization

2014-08-05

国家自然科学基金资助项目(51305026)

U469.72< class="emphasis_italic">DOI

：10.3969/j.issn.1004-132X.2015.11.021

张东好，男，1986年生。北京理工大学机械与车辆学院博士研究生。研究方向为混合动力车辆建模与控制。发表论文10余篇。项昌乐，男，1963年生。北京理工大学机械与车辆学院教授、博士研究生导师。韩立金，男，1982年生。北京理工大学机械与车辆学院讲师。郑海亮，男，1986年生。北京理工大学机械与车辆学院博士研究生。