轮履复合救援机器人的乘适性分析与优化

李　浩　侍才洪　康少华　张西正

1.天津理工大学，天津，300384　　2.军事交通学院，天津，300161 3.军事医学科学院，天津，300161

轮履复合救援机器人的乘适性分析与优化

李浩1,3侍才洪3康少华2张西正3

1.天津理工大学，天津，3003842.军事交通学院，天津，300161 3.军事医学科学院，天津，300161

研究了一种新型轮履复合式救援机器人，它可通过轮履结构的转换在灾难现场等复杂环境中高效地解救和运送伤员。出于对解救伤员在运送过程中安全性、舒适性的考虑，对救援机器人以轮式状态运送伤员的过程进行了振动分析，并利用ADAMS建立救援机器人轮式结构的动力学模型，对其在实际路况的运行进行了仿真分析。考虑人体不同部位不同方向具有不同的频率加权，利用MATLAB设计相应滤波器对仿真所得振动曲线进行处理以计算救援机器人的乘适性。以获取更好的乘适性为目标，通过MATLAB优化工具箱对救援机器人悬架参数进行了优化设计，并进一步验证了优化结果的合理性。

轮履复合；动力学分析；乘适性；优化设计

0　引言

近年来国内外对救援机器人的研究开发日益重视，并已取得显著成就[1]。目前的救援机器人不仅能够探测发现伤者，还具有转运伤员的功能，比较典型的有日本救援机器人RoboCue。本文研究的救援机器人是一种应用于灾难现场救援的机器人，具有搜救并转送伤员的功能。由于救援机器人的工作环境通常为复杂多变、不可预测的非结构环境，故为了提高救援效率，救援机器人采用轮履复合式结构[2]。

救援机器人解救的多为骨折、烧伤、大量出血等伤势较重的伤员，不能再对其产生二次伤害，否则会给伤员带来更大的疼痛，并使伤情恶化，甚至危及生命。因此，救援机器人在转运伤员的过程中必须考虑乘适性[3]。轮履复合式救援机器人有轮式和履带式两种工作状态，可根据不同路况要求快速地进行轮履结构间的转换。通常轮式相对于履带式有较高的行进速度、较好的平稳性，可用于快速转运伤员，但在实际转送伤员过程中，救援机器人结构特殊性等因素会对其乘坐舒适性产生影响，需要加以分析计算。

本文研究的是一种新型轮履复合式救援机器人，目前国内外相关的研究和报道相对较少。本文将车辆行驶动力学的相关理论和救援机器人的自身结构相结合，对救援机器人轮式状态高速运行的乘适性进行分析并做出相应的优化。

1　救援机器人结构简介

本文研究的救援机器人沿用一款全地形车(ATV)的悬架系统，前后均为独立悬架。与一般轮履复合式结构不同，救援机器人行走系统采用轮履复合变体轮，四轮独立驱动。配备有超声波传感器、红外传感器等辅助装置，可以准确识别出伤员。救援机器人配备有两个机械臂，在救援过程中，救援机器人可以自行调整到适当位置，通过机械臂和输送装置的相互协调配合，将伤者安全平稳地以平躺姿势传送至一个小型的救援舱室中。

轮履复合变体轮是一种由驱动主轮、可变形履带、伸展机构及传动机构等组成的新型轮系。在较好的路况下，变体轮以轮式状态行进以保证救援机器人具有较高的速度；在复杂地形下，变体轮可由内部伸展机构展开成三角履带以达到高通过性的要求。图1为变体轮工作原理图。

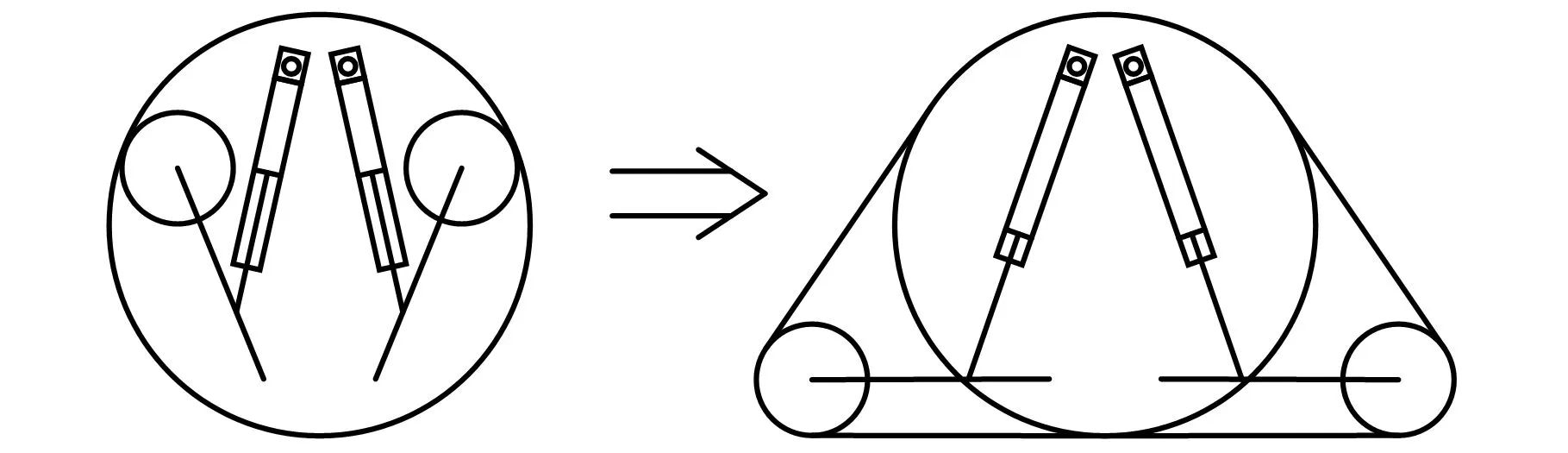
图1　轮履复合变体轮原理图

为实现轮履结构转换，变体轮外侧不同于普通充气轮胎，而是由若干节分段的橡胶履带节相互连接组成的近似圆形的“履带轮”，实物如图2所示。

图2　履带节示意图

变体轮内部有复杂的机构，并且外侧包覆有分段履带，质量较一般车轮大且橡胶履带较常见充气轮胎刚度偏大。外侧橡胶履带结构的不连续性会产生未知激励，对救援机器人的乘适性产生直接影响。

2　乘适性分析

乘坐舒适性可以用乘坐人员所感觉到的振动加速度作为评价指标[2]。在此建立救援机器人的振动模型并考虑救援机器人的结构特殊性，对其振动特性进行分析。

2.1救援机器人振动研究

轮履复合式救援机器人整体结构近似对称于纵轴线，其模型可简化为图3所示的二分之一振动模型[4-5]。图3中，下标f表示前桥，r表示后桥。

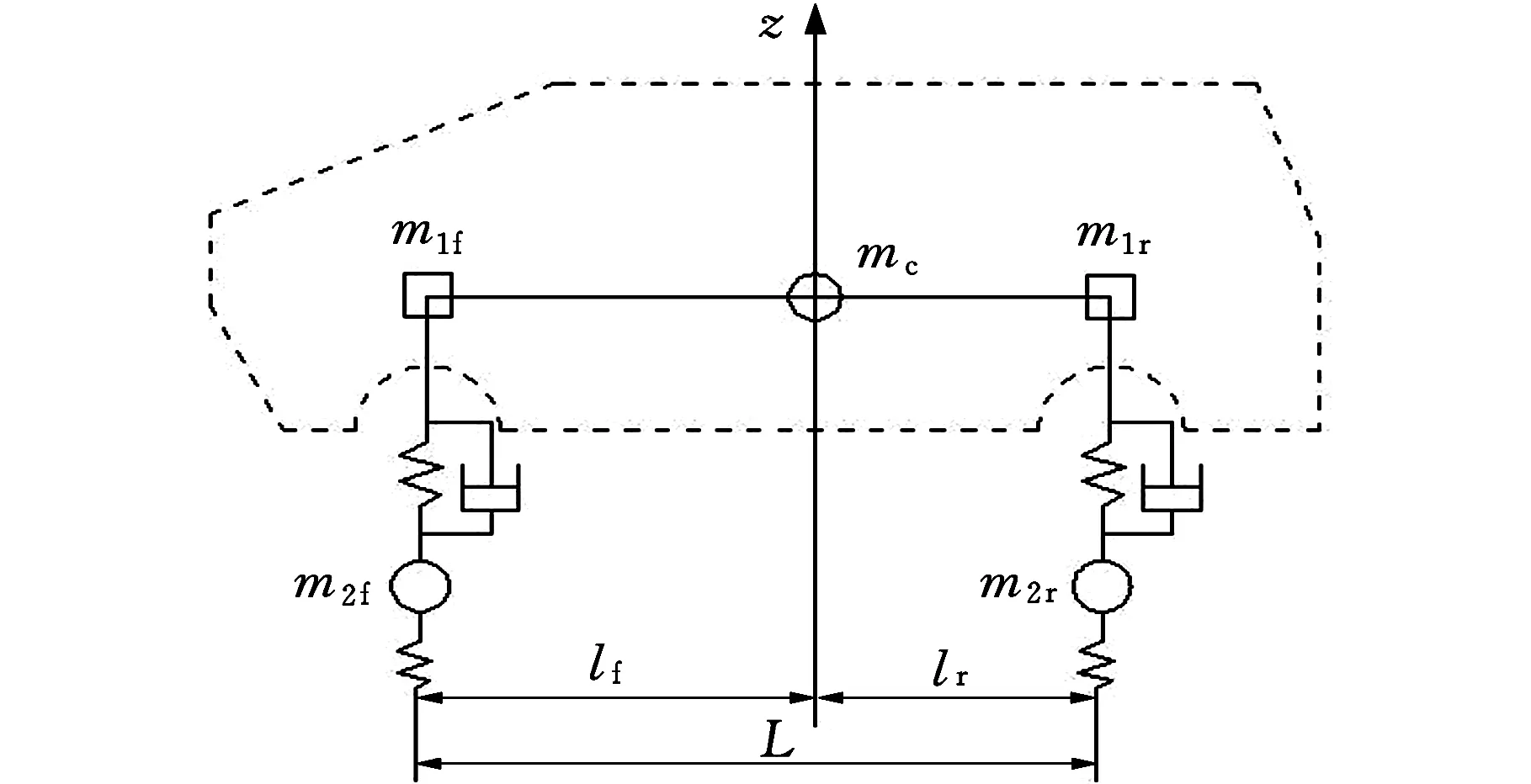
图3　车体二分之一振动模型

车身质量可以等效为三个集中质量：前置质量m1f、联系质量mc和后置质量m1r。根据动力学等效条件有：

(1)系统总质量保持不变，即m1f+mc+m1r=m1；

(2)质心位置不变，即m1flf-m1rlr=0；

可以计算得到三个集中质量分别为

(1)

车轮部分固有频率为

(2)

其中，各量符号的意义及取值如表2所示。

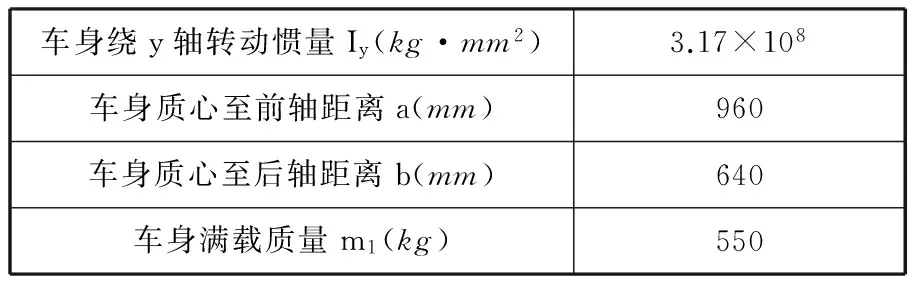
表1　救援机器人车身参数

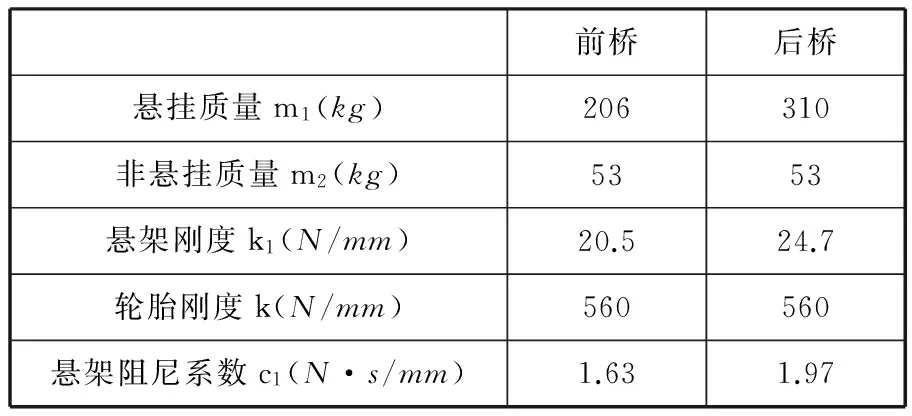
表2　车体振动模型相关系数取值

将表2数据代入式(1)、式(2)可得：ωdf=9.0rad/s≈1.4Hz；ωaf=104.6rad/s≈16.6Hz；ωdr=8.7rad/s≈1.4Hz；ωar=105.0rad/s≈16.7Hz。

变体轮通过外侧履带与地面直接接触，相应轮胎刚度较一般小型车辆的车轮刚度大，由计算得出车轮垂直跳动的固有频率较一般车辆固有频率(10Hz左右)高。对于常见路面，较高频率时道路加速度输入的幅值会有所增大[3]，在设计中应尽量保证较低的固有频率以达到最佳隔振效果。所以应尽量减小履带节刚度，实际中可以通过增加履带外侧挂胶层的厚度、减小橡胶的硬度以及改变履带节外侧的橡胶花纹形状等方式实现。

变体轮外侧履带节之间的不连续可以看作是形状的不完整，并且沿圆周方向均匀分布。该不完整度表现为车轮的径向偏心，会对车轴产生径向高阶谐量激振力，该激振力阶数等于外侧履带的节数。在此将此激振力作为外部激振，研究救援机器人的响应。该激振力的频率为

(3)

式中，n为车轮转速；v为车轮线速度；n′为激振力阶数，n′=27；r为变体轮行驶半径。

救援机器人行驶速度v取值范围为15～60 km/h，则激振力频率f的变化范围为60～240 Hz。可以看出，车轮不连续性造成的激振力频率范围远离车轮固有频率(16.6～16.7 Hz)和车身固有频率(1.3～1.4 Hz)，并且这种偏离与救援机器人的行进速度成正比。因此在救援机器人高速运行过程中，悬架系统可以将该激振力造成的振动较好地隔离。

2.2仿真模型构建

考虑到救援机器人实际运行工况多为沥青、水泥硬路面，所以选取B级路面作为仿真路面。利用ADAMS/View建立仿真模型，如图4所示。以机器人行驶方向为x轴，侧向为y轴，垂直方向为z轴。对4个轮子同时添加驱动转矩，使救援机器人速度稳定于50 km/h，作为观测速度。

图4　救援机器人仿真模型

考虑伤员以卧姿乘坐，在分析乘适性时应分别对伤员头下、后背和盆骨三个直接接触部位的支撑面进行测量[5]，分别定义该三个部位为A、B和C点，分别测量三点x、y、z轴向的加速度曲线。

2.3乘适性评价分析

对任意一点D点进行乘适性分析，对于D点i(i=x,y,z)轴加速度时间历程aDi(t)有

则D点i轴方向频率加权加速度均方根值为

(4)

其乘坐值(乘适性)分量avDi=KDiaWDi。其中，KDi为D点i轴轴向加权系数，对于人体的卧姿振动模型[6]，有KDx=KDy=KDz=1。

则D点的总乘坐值为

(5)

本文为了简化计算，使用频率加权函数滤波器对加速度的时域曲线进行滤波得到aWAi。

巴特沃斯滤波器具有合适的衰减陡度和很好的瞬态特性，且幅度响应带内比较平缓，可以与频率加权函数曲线较好地啮合。用MATLAB设计巴特沃斯滤波器对加速度曲线进行滤波处理以替代加权方式。

国际标准化组织于1997年公布的ISO 2631-1:1997(E)《人体承受全身振动评价——第一部分：一般要求》中提到用加权均方根加速度的基本评价方法，并提供不同部位不同轴向的频率加权函数曲线。参考标准知：B、C点垂直方向频率加权系数为Wk，A、B、C点水平方向频率加权系数为Wd，A点垂直方向频率加权系数为Wj。

以垂直方向频率加权系数Wk为例，对标准函数曲线与所设计的频率加权函数滤波器的幅频特性曲线进行对比，如图5所示。可以看出，本文设计的滤波器与实际的加权标准有一定程度偏差，但很好地保留了对人体敏感的频率带2～12.5 Hz；高频区域对人的主观感觉影响不大，滤波器对高频的阻断对评价结果影响可以忽略[4]。对某时间段B点垂直加速度曲线进行滤波，如图6所示。可以看出，垂直方向上通过带通滤波器滤波后，保留了带通部分中高频率段的信号，滤波后的加权加速度时域曲线较滤波前的曲线密集。滤波前后的曲线对比很好地体现了带通滤波器的特点。

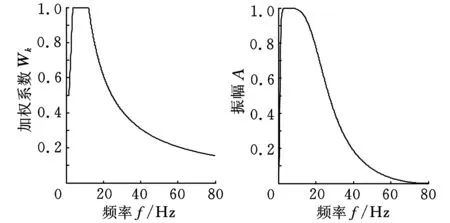
(a)频率加权函数的标准曲线(b)频率加权函数滤波器幅频特性曲线图5　曲线对比

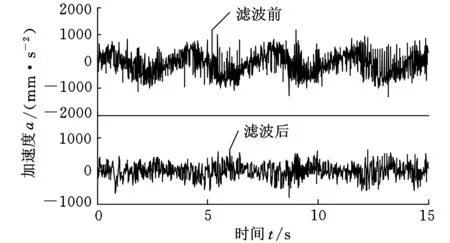
图6　B点垂直方向滤波前后加速度曲线

2.4乘适性评价结果

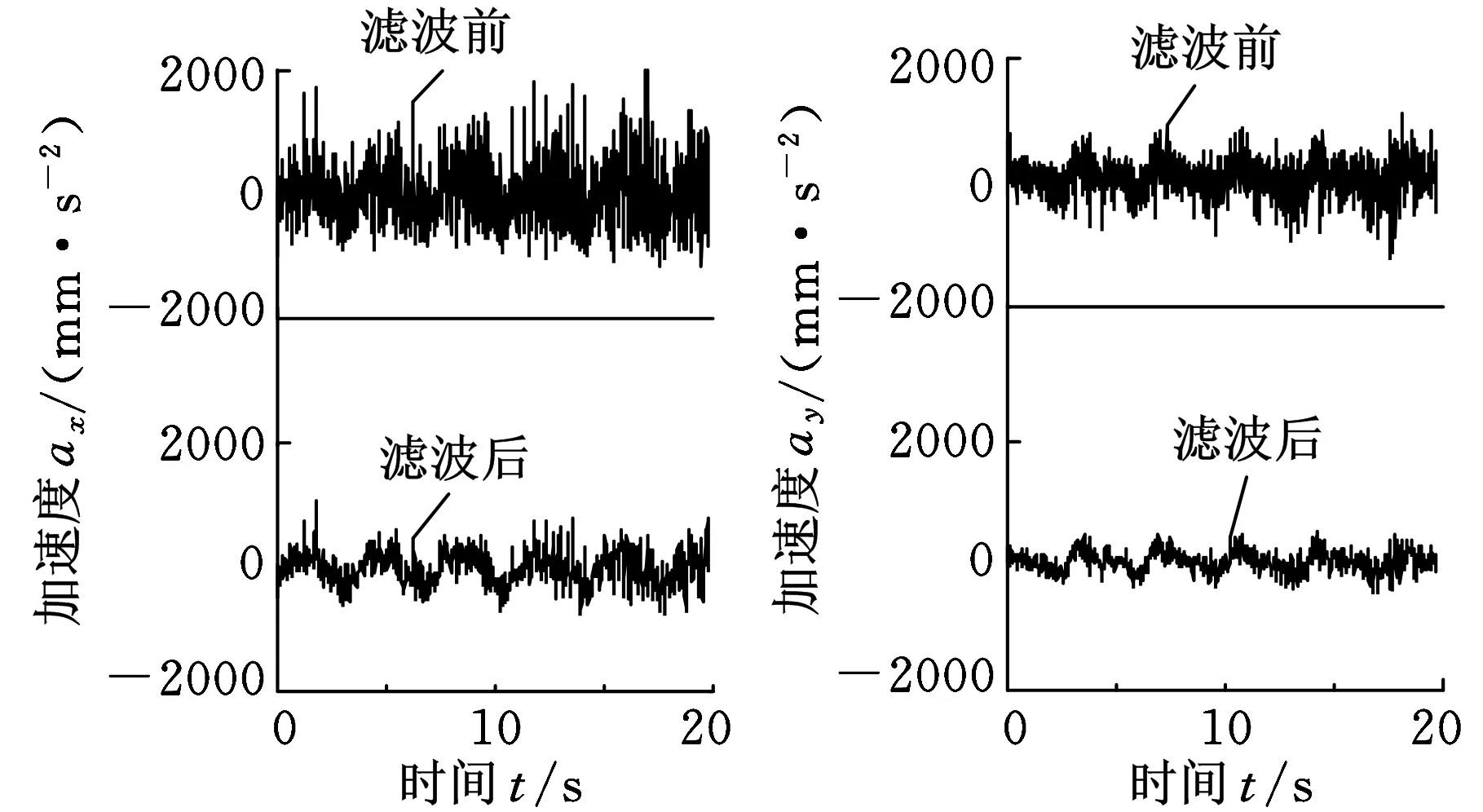
(a)滤波前后x轴加速度(b)滤波前后y轴加速度

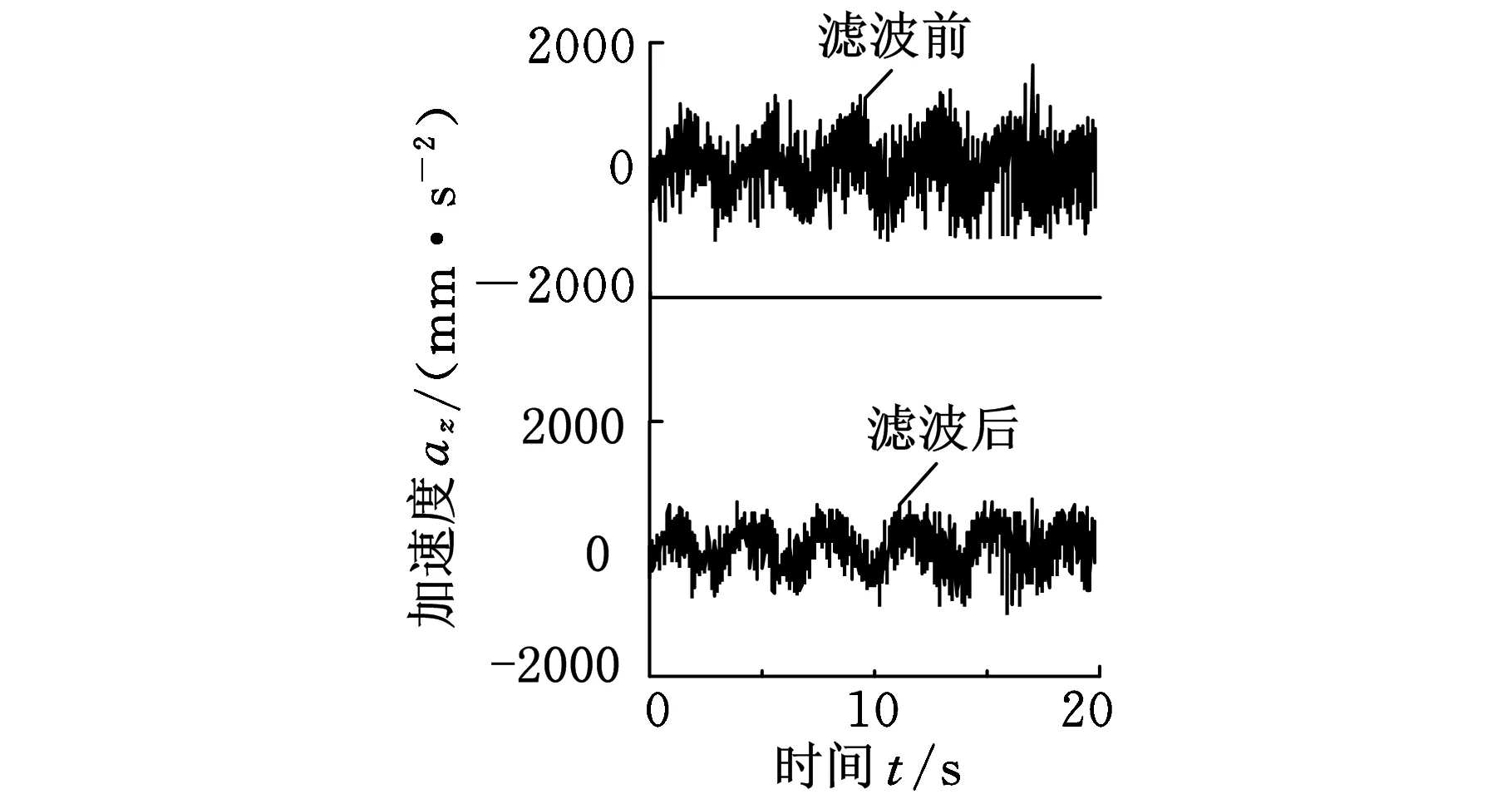
(c)滤波前后z轴加速度图7　A点各轴方向滤波前后加速度曲线

以A点为例，其滤波前后加速度曲线如图7所示。对滤波后加速度曲线作均方根值计算，可以得到A点三个轴向的乘坐值，如表3所示。

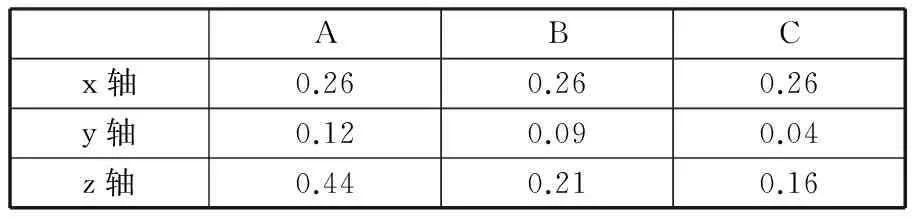
表3　各点各轴向的乘坐值　mm/s2

A、B、C点各轴向总乘坐值分别为

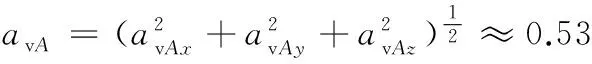
avB≈0.35m/s2

avC≈0.31m/s2

总乘坐值与人的主观感觉的大致关系如表4所示。由计算结果可以看出， A、B、C点位置伤员的主观感觉都会有一些不舒适，且以头下(A点)部位感觉最差。因此有必要对救援机器人的悬架等参数进行优化以改善其乘适性。

表4　总乘坐值与人的主观感觉的大致关系[7]

3　乘适性优化分析

3.1振动模型平顺性分析

以悬架系统的参数为变量进行优化是为了获取良好的平顺性[8]，所以本文以A、B、C点的加速度作为优化对象。对于图3所示模型，其受地面激励的振动微分方程可以表示为

式中，I为转动惯量；φ为车身俯仰角度；qf、qr分别为前后轮地面激振。

表示为矩阵形式为

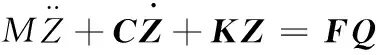
(6)

两侧取傅里叶变换得频率响应函数矩阵：

(7)

以A点为例，设A点与救援机器人质心纵向距离为l，则A点垂直方向振动的频率响应函数为

HA(ω)=Hs(ω)+lHp(ω)

(8)

A点相应的功率谱为

(9)

式(6)～式(9)中各量的含义请参考文献[4]。其中，Sq(ω)为路面输入功率谱密度，由于路面不平度对前轮与后轮的输入不同步，有：

(10)

式中，n0为参考空间频率，n0=0.1 m-1；Gq(n0)为路面不平度系数，对不同不平度等级路面有不同取值。

A点垂直方向加速度加权均方根值为

(11)

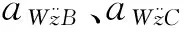
3.2优化设计

本文使用MATLAB优化工具箱进行优化设计[9]，以原始的悬架参数作为初始值，并根据实际悬架设计中的有关经验及规定设置相关约束条件。

根据悬架设计中车辆满载的悬架偏频统计范围，同时综合考虑救援机器人的质心偏后侧，前悬架刚度kf的取值范围为14 200～30 500 N/m，后悬架刚度kr的取值范围为17 400～32 000 N/m。另外，前后悬架系统动挠度的频率响应函数为

Hf d(ω)=Hs(ω)+lfHp(ω)-Hf(ω)

(12)

Hrd(ω)=Hs(ω)+lrHp(ω)-Hr(ω)

(13)

同于式(9)，并考虑悬架击穿的可能性，则悬架系统动挠度的均方根值需满足：

(14)

(15)

式中，sf、sr分别为前后悬架动行程的容许值。

设置优化变量为

优化方程为

优化前后的悬架参数值如表5所示。

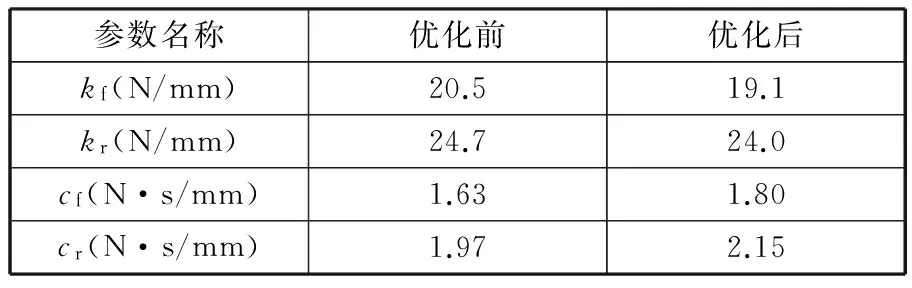
表5　优化前后悬架参数值

修改模型参数，再次仿真，结果如图8所示。

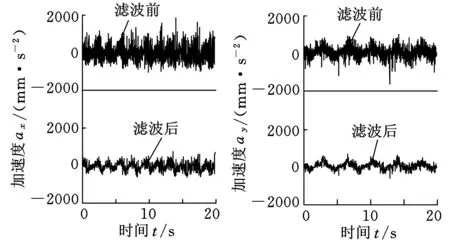
(a)滤波前后x轴加速度(b)滤波前后y轴加速度

(c)滤波前后z轴加速度图8　优化后A点各轴向滤波前后加速度

对曲线进行处理计算后，可得各点各轴向的乘坐值，如表6所示。则各轴向总乘坐值分别为：avA≈0.31 m/s2；avB≈0.28 m/s2；avC≈0.27 m/s2。

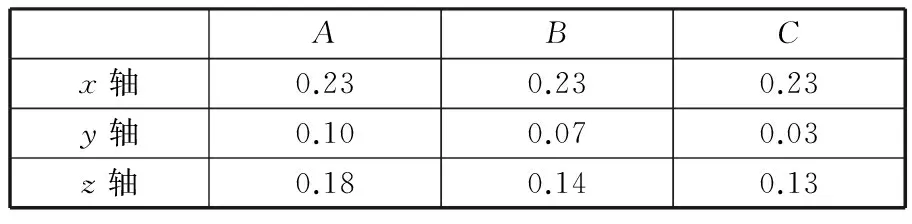
表6　优化后各点各轴向的乘坐值　mm/s2

4　讨论

由以上计算结果可以看出，通过悬架参数优化后，A、B、C三点的总乘坐值均小于0.315 m/s2，伤员没有感觉不舒适，救援机器人的乘适性得到了改善。

对比表3、表6数据，可以看出：①三个测试点行驶方向(x轴向)的乘坐值大体相同，但是由于三个测试点与救援机器人车身质心距离lA>lB>lC，A点横向和垂直方向的加速度均较B、C点大。②救援机器人是近似对称结构，各点横向加速度相对较小，但是垂直方向的乘坐值均偏大，是影响救援机器人乘适性的关键因素。③以悬架参数作为变量进行优化，优化结果可通过直接改善救援机器人垂直方向的振动特性来改变各点垂直方向的乘坐值。

5　结论

(1)建立了救援机器人振动模型，分析了救援机器人的结构特殊性对其乘适性的影响。变体轮外侧橡胶履带的结构不连续性会引起径向激振，通过计算，该激振力所产生的振动频率范围为60～240Hz，对机器人乘适性影响不大；但由于变体轮履带节刚度过大，会使车轮部分固有频率较常值偏大，使得较高频率激振下的乘适性变差。

(2)针对救援机器人的综合乘适性，以悬架参数作为优化变量，以三个关键测试点的总乘适性均方值作为优化目标进行优化分析，进一步的仿真分析结果显示，优化后的悬架系数改善了救援机器人的乘适性，从而验证了本文优化方法的正确性。

[1]刘金国，王越超，李斌,等.灾难救援机器人研究现状、关键性能及展望[J].机械工程学报，2006，42(12)：1-12.

LiuJinguo,WangYuechao,LiBin,etal.CurrentResearch,KeyPerformancesandFutureDevelopmentofSearchandRescueRobot[J].JournalofMechanicalEngineering, 2006,42(12):1-12.

[2]罗洋，李奇敏，温皓宇,等.一种新型轮腿式机器人设计与分析[J].中国机械工程，2013，24(22)：3018-3023.

LuoYang,LiQimin,WenHaoyu,etal.DesignandAnalysisofaNewKindofWheel-leggedRover[J].ChinaMechanicalEngineering, 2013,24(22):3018-3023.

[3]GillespieTD. 车辆动力学基础[M].赵六奇，金达锋,译.北京：清华大学出版社，2006.

[4]张立军，何辉.车辆行驶动力学及应用[M].北京：国防工业出版社，2011.

[5]李晓玲，张鄂，陆长德,等.人体生物力学模型的驾驶舒适度仿真研究[J].西安交通大学学报，2008，42(5)：556-560.

LiXiaoling,ZhangE,LuChangde,etal.DrivingComfortSimulationBasedonHumanBiomechanicsModelunderVibration[J].JournalofXi’anJiaotongUniversity, 2008,42(5):556-560.

[6]苏琛，徐新喜，高振海,等.某履带急救车减振效率及乘卧舒适性分析[J].振动、测试与诊断，2012，32(5)：854-857.

SuChen,XuXinxi,GaoZhenhai,etal.TheAnalysisofaTrackedAmbulanceDampingEfficiencyandRideComfort[J].JournalofVibrationMeasurement&Diagnosis, 2012,32(5):854-857.

[7]丁法乾.履带式装甲车辆悬挂系统动力学[M].北京：国防工业出版社，2004.

[8]王德平，郭孔辉，宗长富,等.车辆动力学稳定性控制的理论研究[J].汽车工程，2000，22(1)：7-9.

WangDeping,GuoKonghui,ZongChangfu,etal.TheoreticalStudyonVehicleDynamicsStabilityControl[J].AutomotiveEngineering, 2000,22(1):7-9.

[9]BouazaraM,RichardMJ.AllOptimizationMethodDesignedtoImproveVehicleComfortandRoadHoldingCapabilitythroughtheUseofActiveandSemi-activeSuspensions[J].EuropeanJournalofMechanicsandSolids, 2001,20(3):509-502.

(编辑袁兴玲)

Analysis and Optimization of Ride Comfort for a Wheel-tracked Rescue Robot

Li Hao1,3Shi Caihong3Kang Shaohua2Zhang Xizheng3

1.Tianjin University of Technology,Tianjin,300384 2.Military Traffic Institute,Tianjin,300161 3.Academy of Military Medical Science,Tianjin,300161

This paper presented a new kind of wheel-tracked rescue robot,which could efficiently search and transport the wounded in the disaster sites and other complex environments by converting the structure between wheel and track. Considering the safety and comfort of the wounded,this paper focused on the vibration analysis during the transporting of the wounded, and used the multi-body dynamics software ADAMS to establish the rescue robot’s dynamics model.This model was about the simulation analysis of the operation in the actual road conditions. Considering different parts of the human body have different frequency weighting functions in different directions, the simulation curve should be processed by the corresponding filter designed by MATLAB to calculate the robot’s ride comfort. Target to better ride comfort, the suspension parameters should be redesigned by the MATLAB optimization toolboxes.And the further simulation outcomes demonstrate the rationality of the optimization results.

wheel-tracked; dynamics analysis; ride comfort; optimization design

2014-07-09

军队重大专项(BS312C002)；军事医学科学院创新基金资助项目(2012CXJJ007)

TP242.6< class="emphasis_italic">DOI

：10.3969/j.issn.1004-132X.2015.11.005

李浩，男，1991年生。天津理工大学与军事医学科学院联合培养硕士研究生。主要研究方向为机械设计及理论。侍才洪，男，1982年生。军事医学科学院卫生装备研究所助理研究员。康少华，女，1959年生。军事交通学院军事物流系教授。张西正，男，1955年生。军事医学科学院卫生装备研究所研究员、博士研究生导师。