基于包络谱稀疏度和最大相关峭度解卷积的滚动轴承早期故障诊断方法

2015-10-29唐贵基王晓龙

中国机械工程 2015年11期

关键词：峭度特征频率轴承

唐贵基　王晓龙

华北电力大学,保定,071000

基于包络谱稀疏度和最大相关峭度解卷积的滚动轴承早期故障诊断方法

唐贵基王晓龙

华北电力大学,保定,071000

滚动轴承处于早期故障阶段时,特征信号微弱,并且受环境噪声影响严重,因此故障特征提取困难。针对这一问题,将最大相关峭度解卷积算法应用于轴承故障诊断,并通过包络谱稀疏度来筛选最佳解卷积周期参数,提出了基于包络谱稀疏度和最大相关峭度解卷积的滚动轴承早期故障诊断方法。利用最佳参数相对应的最大相关峭度解卷积算法对原信号进行处理，得到解卷积信号后计算其包络谱，通过分析包络谱中幅值突出的频率成分来判断故障类型。早期故障仿真信号及实测全寿命数据分析结果表明，该方法可有效应用于轴承早期故障诊断。

滚动轴承;稀疏度;最大相关峭度解卷积;故障诊断

0　引言

滚动轴承是旋转机械中的重要组成零部件,其状态正常与否决定了整个系统的性能好坏。当轴承出现局部损伤或缺陷时,轻则使设备产生噪声、振动异常,重则损坏设备，因此研究滚动轴承的状态监测及故障诊断方法具有重要意义[1]。

当轴承处于早期故障阶段时,由故障产生的冲击成分通常比较微弱，并淹没于强烈的背景噪声中，因此想要准确提取出故障特征频率信息相对困难，探寻轴承的早期故障诊断方法也一直是故障诊断领域的热点和难点。文献[2]利用小波相关滤波的降噪特性,将相关滤波降噪方法和包络谱相结合,提出了基于小波相关滤波包络分析的轴承早期故障特征提取方法；为确定由故障引起的共振调制边频带，文献[3]提出了共振解调结合小波包系数熵阈值降噪的综合算法；为准确判断故障类型,文献[4]将双重Q因子分析方法用于轴承早期故障诊断中,原信号被分解成高共振成分和低共振成分,并利用低Q因子来提取故障冲击成分;文献[5]采用基于互相关系数和峭度准则的经验模态分解(EMD)降噪方法对信号进行预处理,再利用谱峭度选取最佳滤波参数,最后使用带通滤波和包络解调进行故障诊断。上述各种方法在轴承早期故障诊断应用中均取得了一定的效果。

1977年,Wiggins将最小熵概念引入到盲解卷积问题处理中,提出了最小熵解卷积方法,并被广泛应用到地震波处理、超声检测及机械故障诊断等领域[6-7]。最近,McDonald等[8]提出了一种新的解卷积方法——最大相关峭度解卷积(MCKD),该方法以相关峭度最大化为目标,充分考虑了信号中冲击成分的周期特性,旨在突出运算结果中的连续脉冲序列,本文尝试将其引入到滚动轴承故障诊断领域。然而MCKD方法的运算结果受解卷积周期参数T影响严重,为避免实际故障信号处理过程中该参数盲目选择对解卷积效果的影响,笔者以包络谱稀疏度作为指导标准来选择最佳的解卷积周期参数,并提出了基于包络谱稀疏度和最大相关峭度解卷积的滚动轴承早期故障诊断方法，模拟早期故障信号及全寿命周期加速试验信号均验证了该方法的正确性。

1　基本原理介绍[8]

1.1相关峭度和稀疏度

零均值信号y(n)(n=1,2,…,N)关于周期参数T的相关峭度表达式为

(1)

相关峭度是在峭度基础上提出的概念,当T=0时,相关峭度即退化为峭度，该指标由于考虑了冲击成分的周期特性,因此适合衡量信号中具有特定周期的脉冲序列所占的比重，与峭度相比，相关峭度更强调冲击成分的连续性。

稀疏度是反应信号稀疏特性的统计参量,信号y(n)的稀疏度表达式为[9]

(2)

当信号的幅值分布相对均匀、差别不大时,信号的稀疏性较弱,稀疏度指标较小,而当信号中出现少量尖脉冲、个别位置幅值突出时,信号则呈现出较强的稀疏特性，稀疏度指标也随之增大。

1.2最大相关峭度解卷积

假设yn为一个冲击信号,hn为冲击信号yn通过周围环境及路径时的传输衰减响应,xn为实际采集到的信号,以上过程可用公式表示为

xn=hnyn+en

(3)

为便于分析,在此先不考虑噪声en的影响,则MCKD算法的本质是寻找一个有限脉冲响应(FIR)滤波器,通过输出信号xn恢复输入信号yn,即

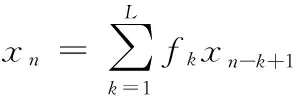
(4)

其中,[f1f2…fL]T=f是长度为L的滤波器系数。

为使解卷积结果突出连续尖脉冲,该算法以信号的相关峭度KC为评定标准,并将其作为目标函数以求得最优结果,即

(5)

上述优化求解问题等价于求解方程：

(6)

由式(4)和式(5)可以得到如下表达式：

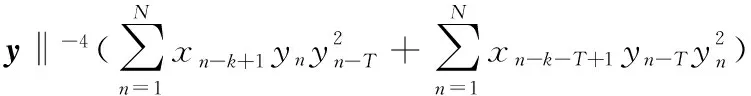
(7)

以矩阵的形式将式(7)重新表述为

4‖y‖-6‖β‖2X0y=0

(8)

β=[y1y1-Ty2y2-T…yNyN-T]T

整理式(8)可得

2‖β‖2X0y=‖y‖2(X0α0+XTα1)

(9)

由于已知：

(10)

则最终的滤波器系数可通过下式得到

(11)

1.3MCKD的数值实现过程

通过上述分析可归纳出最大相关峭度解卷积算法的具体数值实现步骤：

(1)首先确定一个解卷积周期参数T;

(3)设定好FIR滤波器的长度L,并假设初始滤波器系数f=[00…1-1…00]T；

(4)利用式(10)计算滤波后的信号y;

(5)通过y分别计算α0、α1和β；

(6)根据式(11)得到新的滤波器系数f；

(7)比较每次迭代过程的相关峭度变化量ΔKC(T)与阀值ε的大小,如果ΔKC(T)>ε,则返回步骤(4),否则结束整个循环,其中阀值ε是一个较小正数,用于控制迭代次数(本文设定的阀值ε=0.01)。

(8)最终的解卷积信号可由式(10)得到。

2　故障诊断流程

滚动轴承处于故障早期阶段时,冲击特征微弱,而最大相关峭度解卷积可实现信号的解卷积运算,突出信号中的连续脉冲,因此适合处理轴承早期故障信号。笔者研究后发现,在分析实际故障信号时,MCKD算法的处理结果受解卷积周期参数T影响严重,理论上,如果参数T与故障冲击的间隔点相等，则可获得最好的解卷积效果，然而实际故障信号的脉冲间隔是未知的，因此选择最佳的解卷积周期参数、有效突出信号中隐含的周期性脉冲序列是利用MCKD算法进行轴承故障诊断的关键。

稀疏度能够有效反应信号的稀疏特性,可用于评价故障信号解卷积处理的效果，然而时域信号的稀疏度容易受单个或少量大幅值脉冲的影响,因此直接以时域信号的稀疏度作为评价标准并不合适,而将信号转换到频域,计算包络谱的稀疏度则可有效避免这一缺陷。在分析滚动轴承早期故障信号时,经过MCKD算法处理后的信号如果周期性冲击特性不明显,则解卷积信号包络谱各频率处的幅值相差不大，没有峰值突出的成分，包络谱稀疏度相对较小;如果信号中出现较明显的周期性连续脉冲,则包络谱的相应频率处会出现较大谱峰，稀疏度也将随之增大。鉴于上述分析,本文以包络谱稀疏度为指导标准来搜寻最佳的解卷积周期参数，并提出基于包络谱稀疏度和最大相关峭度解卷积的滚动轴承早期故障诊断方法，具体的诊断流程如下：

(1)计算滚动轴承各部件理论故障特征频率。根据轴承结构参数分别计算轴承内圈、外圈、滚动体和保持架的故障特征频率fi、fo、fb和fc。

(3)确定搜索范围。由于实际故障特征频率与理论计算值之间存在一定差别，如果仅在4个搜寻中心点处寻找最佳解卷积周期参数，很可能造成遗漏或产生偏差，而以中心点为中心确定一个搜索范围，在搜索范围内做进一步小范围搜索则可有效避免此类现象发生。从计算成本角度考虑,为加快运算速率本文选择在中心点左右5个点范围内搜索,确定了[Ti-5,Ti+5]、[To-5,To+5]、[Tb-5,Tb+5]和[Tc-5,Tc+5]4个搜索范围(每个范围内有11个连续的数值点),在处理不同信号时，搜索范围大小可根据具体情况作适当缩放调整。

(4)筛选最佳参数。以搜索范围内的数值点为解卷积周期参数,按顺序变化数值点,分别利用MCKD算法对故障信号进行处理,并计算所获信号的包络谱稀疏度,得到4条解卷积周期-包络谱稀疏度曲线。MCKD算法处理原信号时解卷积周期参数越合理,所获解卷积信号中包含的故障特征成分越多,解卷积信号包络谱中特征频率及其倍频处谱峰越突出,包络谱呈现出越强的稀疏特性,稀疏度值也相对较大,因此包络谱稀疏度指标可有效评价解卷积周期参数设置的合理性,选择曲线中稀疏度最大值点对应的参数即为最佳解卷积周期参数Tm。

(5)轴承故障诊断。设定MCKD算法的解卷积周期为Tm,对原故障信号进行处理,并计算解卷积信号的包络谱,将包络谱中幅值明显的频率成分与理论故障特征频率进行对比,从而判断滚动轴承的故障类型。

3　早期故障模拟信号分析

为验证基于包络谱稀疏度和最大相关峭度解卷积的滚动轴承早期故障诊断方法的可靠性,本文通过向实测振动信号中添加高斯白噪声来模拟早期故障信号。首先在千鹏故障(QPZZ)试验平台上利用内置电路(ICP)压电加速度传感器采集轴承内圈故障振动信号,采样频率为12 800 Hz,分析点数为8192,传动轴转速为1440 r/min,滚动轴承各部件的理论故障特征频率如表1所示。

大部分文献利用模拟信号验证所提出的轴承早期故障诊断方法的有效性时,均采用故障模型来模拟早期故障信号,为更接近实际工况,本文直接向实测信号中添加较重噪声来模拟轴承早期故障信号，早期故障信号信噪比rSN为-12 dB,计算公式为

rSN=20lg(ν/νn)

(12)

式中,ν、νn分别为实测振动信号和噪声的有效值。

振动信号和模拟早期故障信号如图1所示。

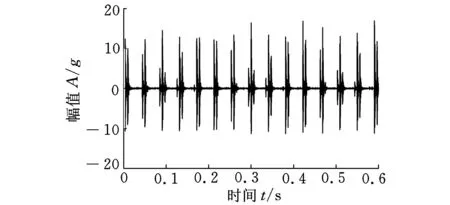
(a)振动信号

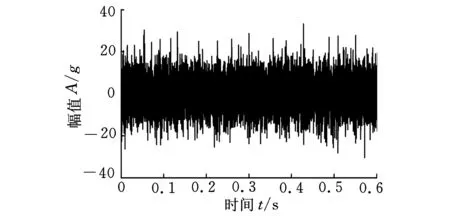
(b)模拟早期故障信号图1　振动信号和模拟早期故障信号

通过对比可发现,添加白噪声后,实测振动信号中明显的规律性冲击完全被噪声所掩盖，图2所示是对模拟早期故障信号直接作包络谱分析得到的结果,包络谱中没有出现峰值明显的频率成分。

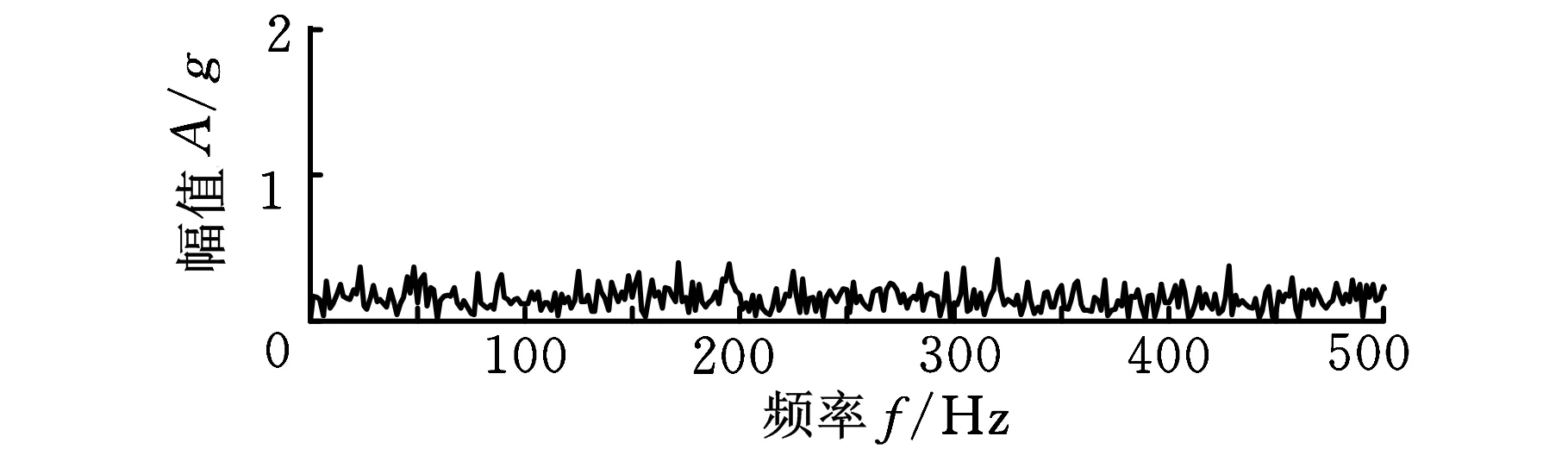
图2　模拟早期故障信号的包络谱

利用本文提出的方法对信号进行分析,结果如图3所示。首先需确定最佳解卷积周期参数的搜索范围,根据采样频率及各部件故障特征频率计算得到[70,80]、[105,115]、[208,218]和[1315,1325]4个搜寻范围。以这4个范围内的数值点为MCKD算法的解卷积周期参数,依照顺序不断变动参数,分别对模拟早期故障信号作最大相关峭度解卷积运算,并计算获得信号的包络谱稀疏度,得到图3a所示的4条解卷积周期-包络谱稀疏度曲线(T-S曲线)。分析这些曲线后发现最大稀疏度指标对应的解卷积周期为75,由此确定最佳解卷积周期参数Tm=75,设定MCKD算法的解卷积周期参数为75并对信号进行处理,结果如图3b所示。与原信号对比后发现，解卷积信号中冲击成分明显增多,并呈现出一定的规律性。图3c为解卷积信号的包络谱,图中内圈故障特征频率fi及其倍频、转频fr及其倍频、特征频率的转频调制边带等成分处谱线峰值明显,由此可断定,轴承内圈存在缺陷，诊断结果与实际情况相符。

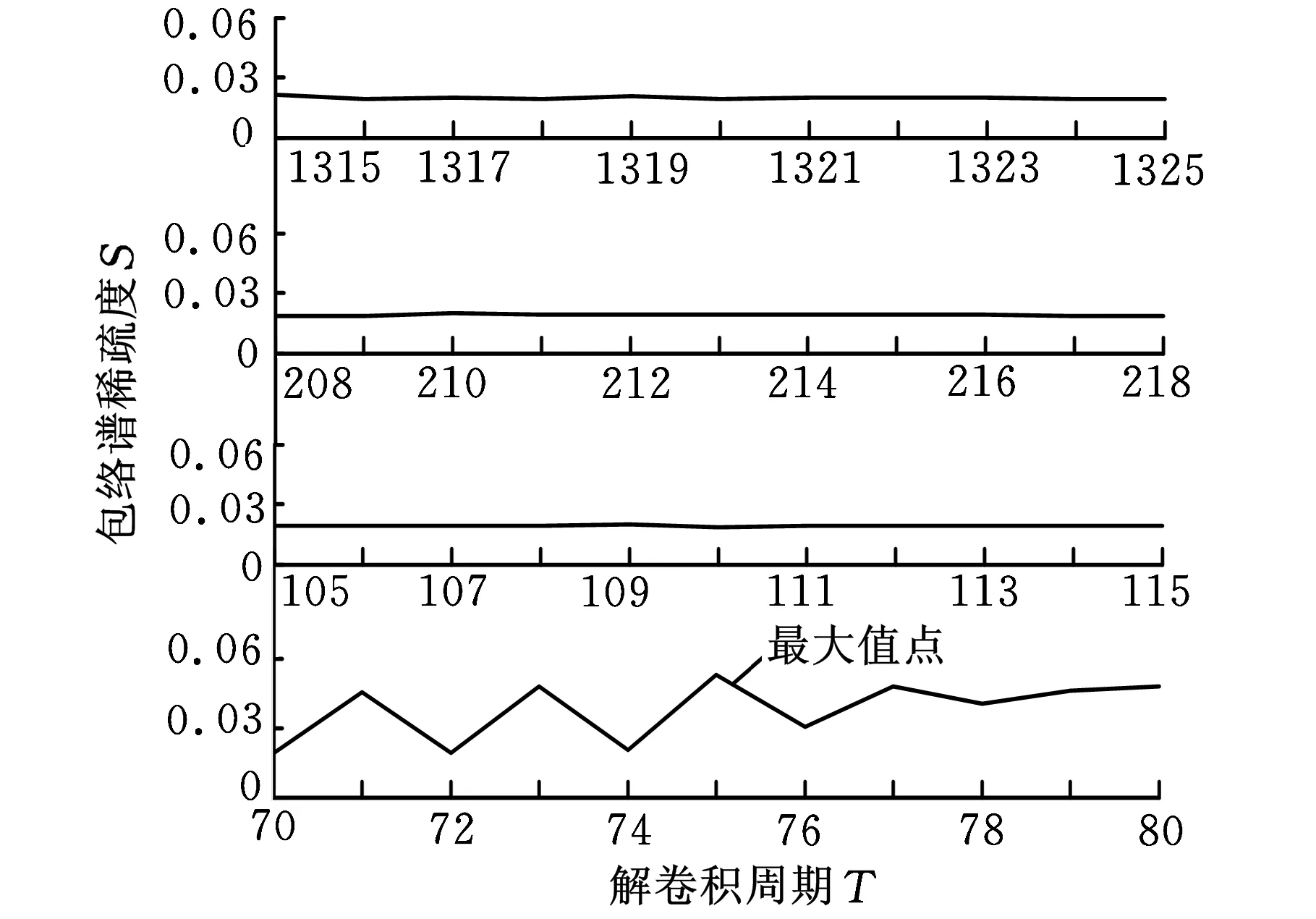
(a)T-S曲线

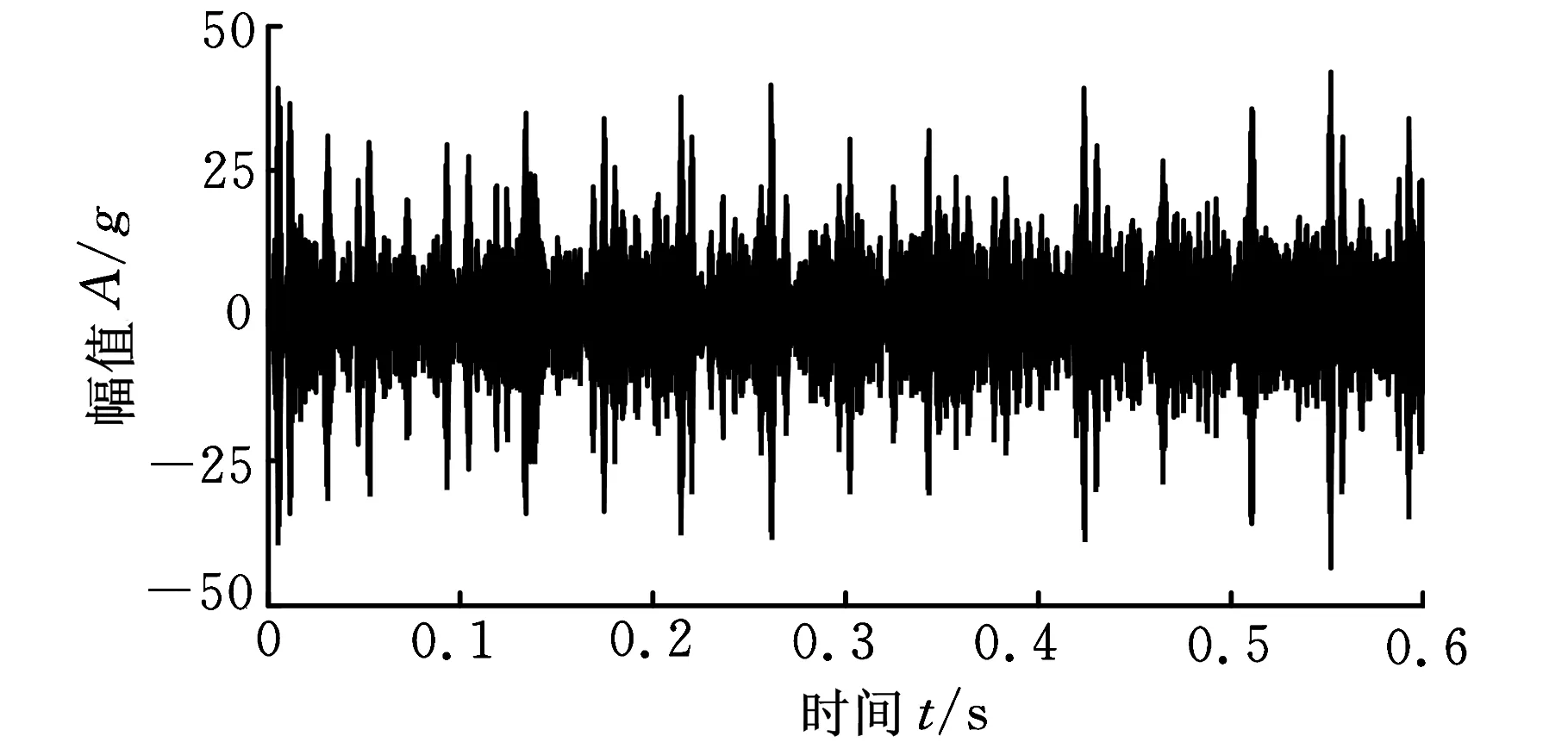
(b)最大相关峭度解卷积信号

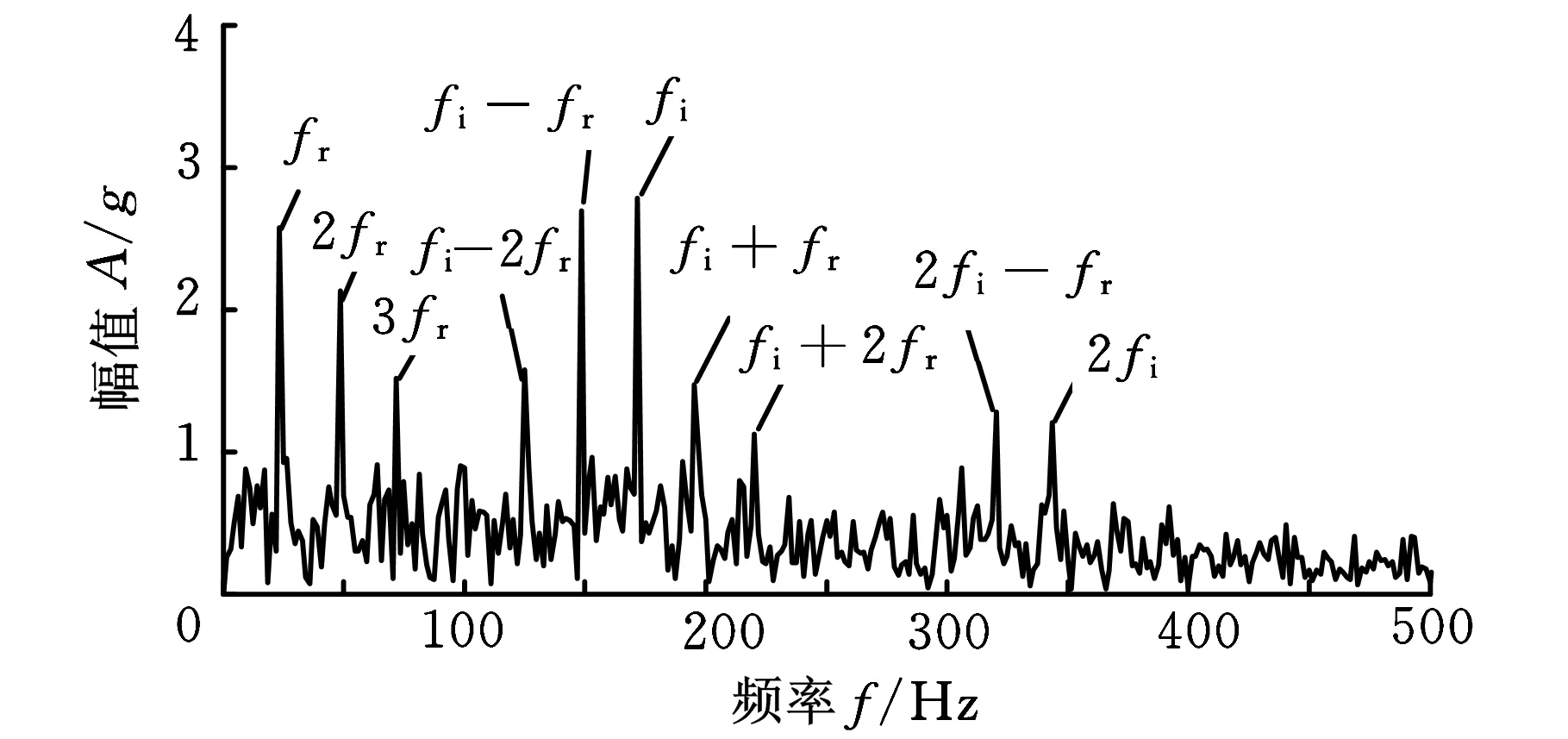
(c)解卷积信号的包络谱图3　本文方法的模拟信号分析结果

仿真信号分析表明，当信号中与故障相关的冲击特征被较强背景噪声淹没时,如果直接对其做包络谱分析，可能无法有效提取出特征频率信息，而利用本文提出方法对原信号进行分析后，能够获得较理想的处理效果，实现轴承故障类型的准确判断。

4　应用实例分析

实例分析数据来自于NSFI/UCR智能维护系统中心的滚动轴承全寿命周期加速试验数据[10],试验台转轴上同时安装了4个轴承,转速恒定在2000 r/min,约26 671 N的径向载荷通过弹性系统加载到轴和轴承上,每个轴承的轴向和径向各安装了一个PCB公司生产的353B33型高灵敏度ICP加速度传感器,图4给出了轴承和传感器的安装位置,表2为试验轴承各部件的理论故障特征频率。

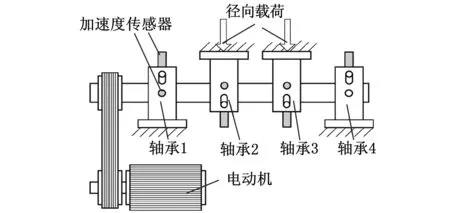
图4　试验台示意图

利用NI DAQCard-6062E采集卡采集振动信号,采样频率为20 kHz,共进行了3组全寿命加速试验,其中第2组试验持续了164 h,共采集984个文件,采样间隔为10 min,每次采集20 480个点,试验结束后发现1号轴承外圈出现局部损伤,说明第2组试验中只有该轴承的数据为全寿命数据,本文便对该轴承的实测数据进行分析,图5为轴承振动信号的均方根值趋势图。

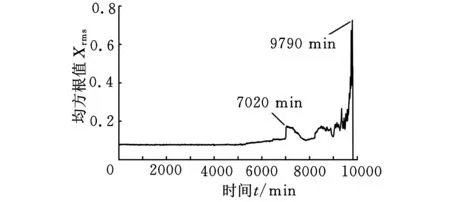
图5　1号轴承振动信号的均方根值趋势图

图5中均方根值的变化趋势基本反映了轴承从正常状态到故障状态的全过程。在7020 min之前,轴承运行相对稳定;当运行至7020 min时,振动信号均方根值发生微小突变,表明轴承状态发生异常;在7020～9000 min时间段内,均方根值上下浮动,但变化幅度不大,说明轴承故障程度并不严重；当运行时间超过9000 min后,轴承振动信号均方根值呈连续递增变化趋势,并在9790 min时达到最大,此时轴承已达到寿命极限，出现严重故障。由于轴承早期故障的冲击特征较微弱，容易被噪声掩盖而无法直接从原始波形中观察到，所以振动信号的均方根值对早期故障并不敏感。

为验证本文方法在轴承早期故障诊断应用上的可靠性,对5410 min时采集的信号进行分析,分析点数为8192,实测信号如图6所示,通过波形观察不到明显的故障特征，对信号做进一步包络谱分析，如图7所示，也没有发现幅值较高的频率成分。

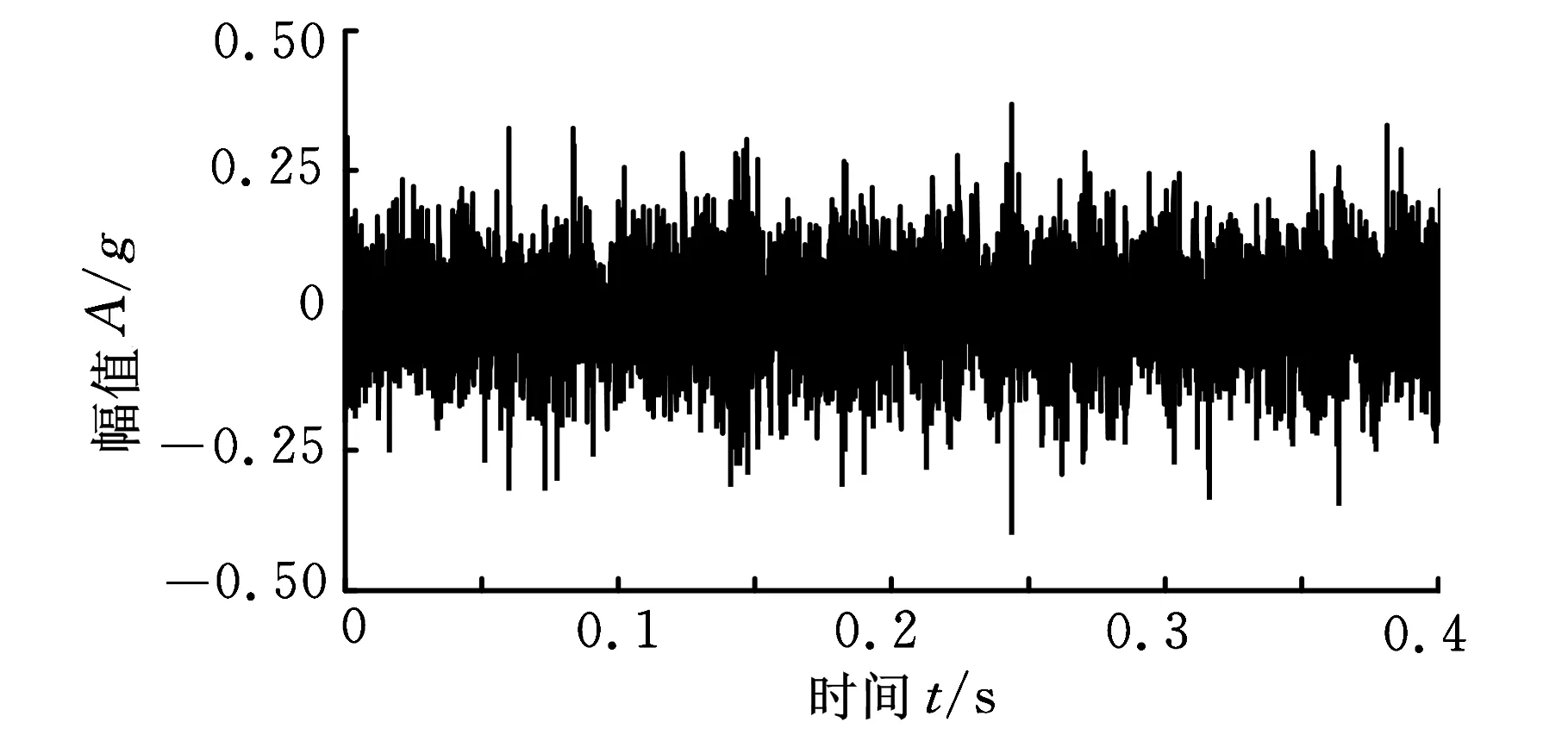
图6　实测信号

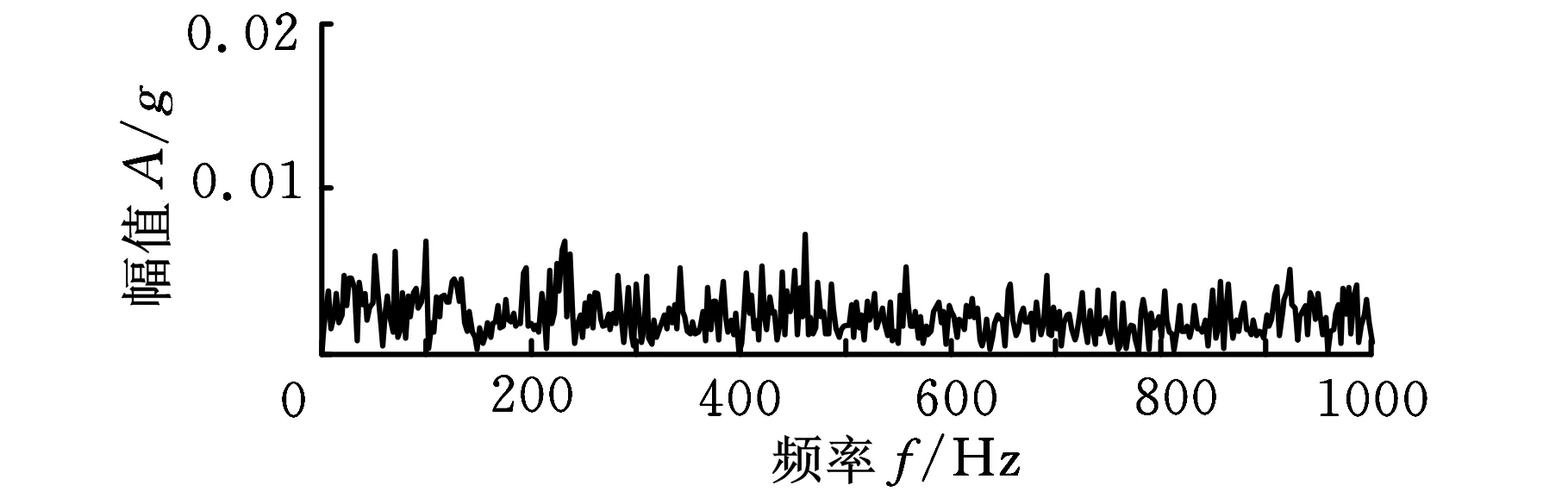
图7　实测信号的包络谱

下面利用本文方法对信号进行处理,结果如图8所示。首先根据采样频率fs=20 kHz、轴承内圈特征频率fi=296.9 Hz、外圈特征频率fo=236.4 Hz、滚动体特征频率fb=140 Hz及保持架特征频率fc=14.8 Hz得到最佳周期参数的搜索中心和范围,其中获得的4个搜索中心分别为Ti=67，To=85，Tb=143，Tc=1351,与搜索中心相对应的4个搜索范围分别为[62,72]、[80,90]、[138,148]、[1346,1356],继而绘制出图8a中的T-S曲线。通过分析可知解卷积周期为85时稀疏度指标最大,则85即为最佳的解卷积周期参数Tm,设定MCKD算法的解卷积周期参数为85并对实测信号进行处理,所得结果如图8b所示。进一步计算解卷积信号的包络谱,结果如图8c所示,包络谱中外圈故障特征频率fo及其谐波处幅值突出,由此可断定轴承外圈存在局部损伤,理论分析结果与实际情况完全一致。

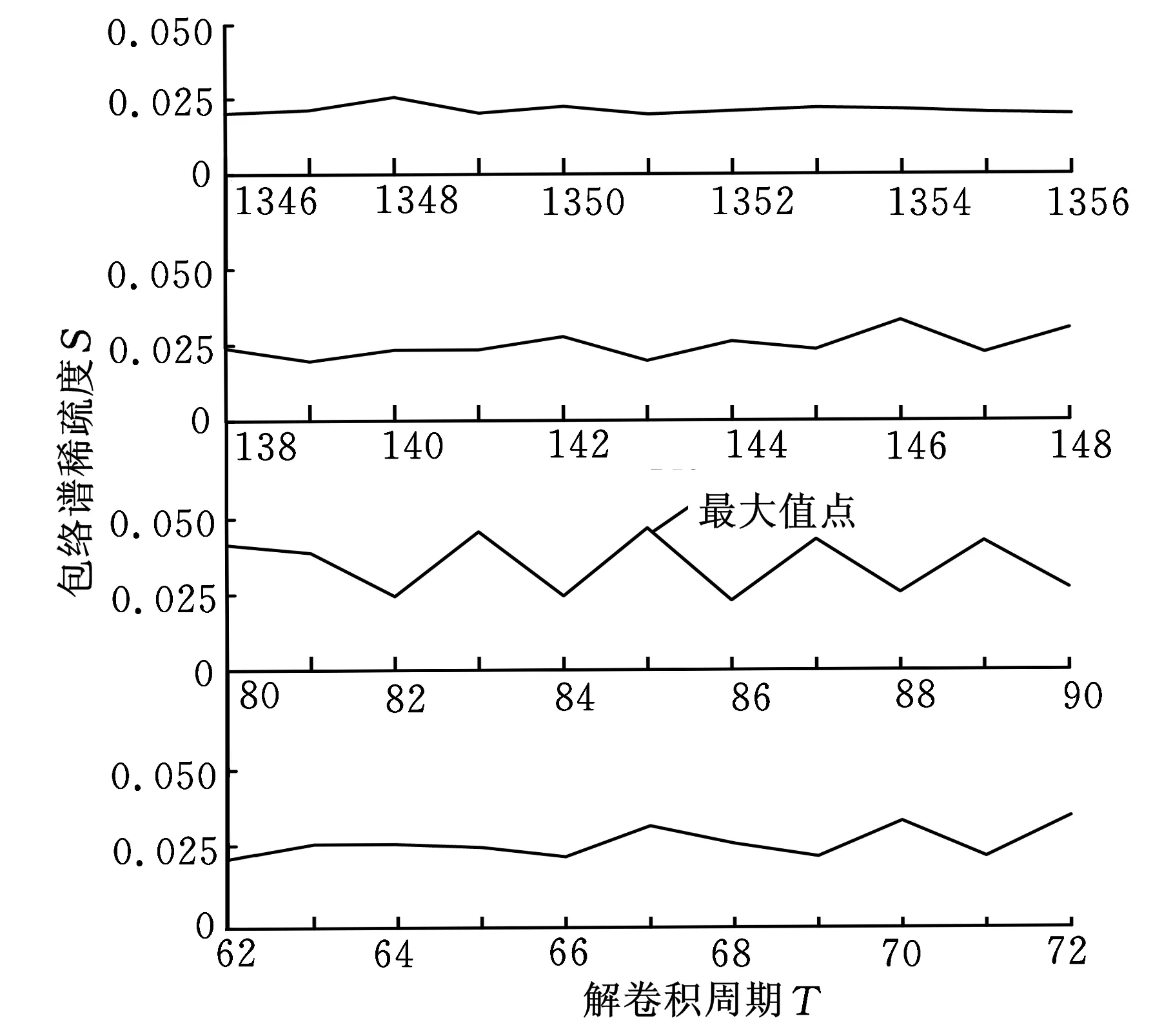
(a)T-S曲线

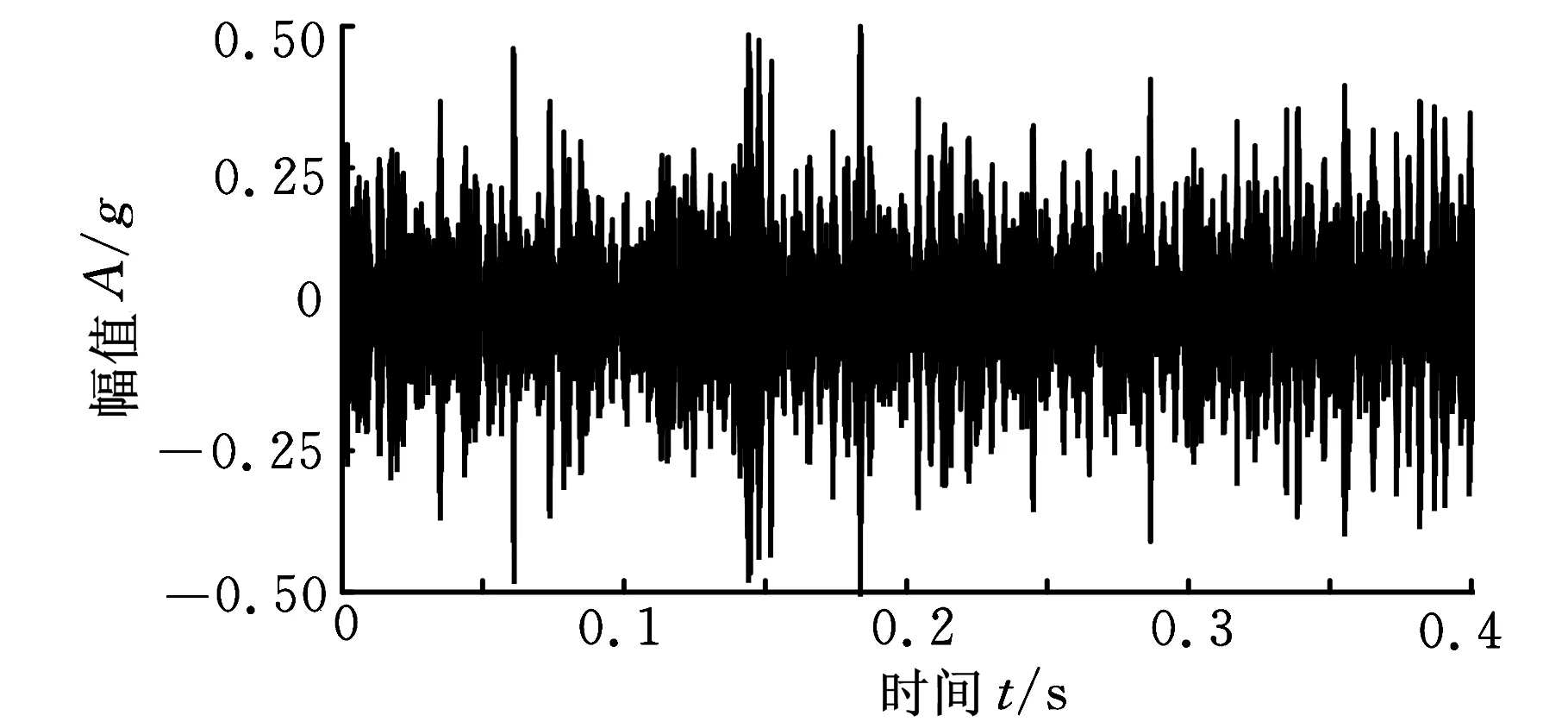
(b)最大相关峭度解卷积信号

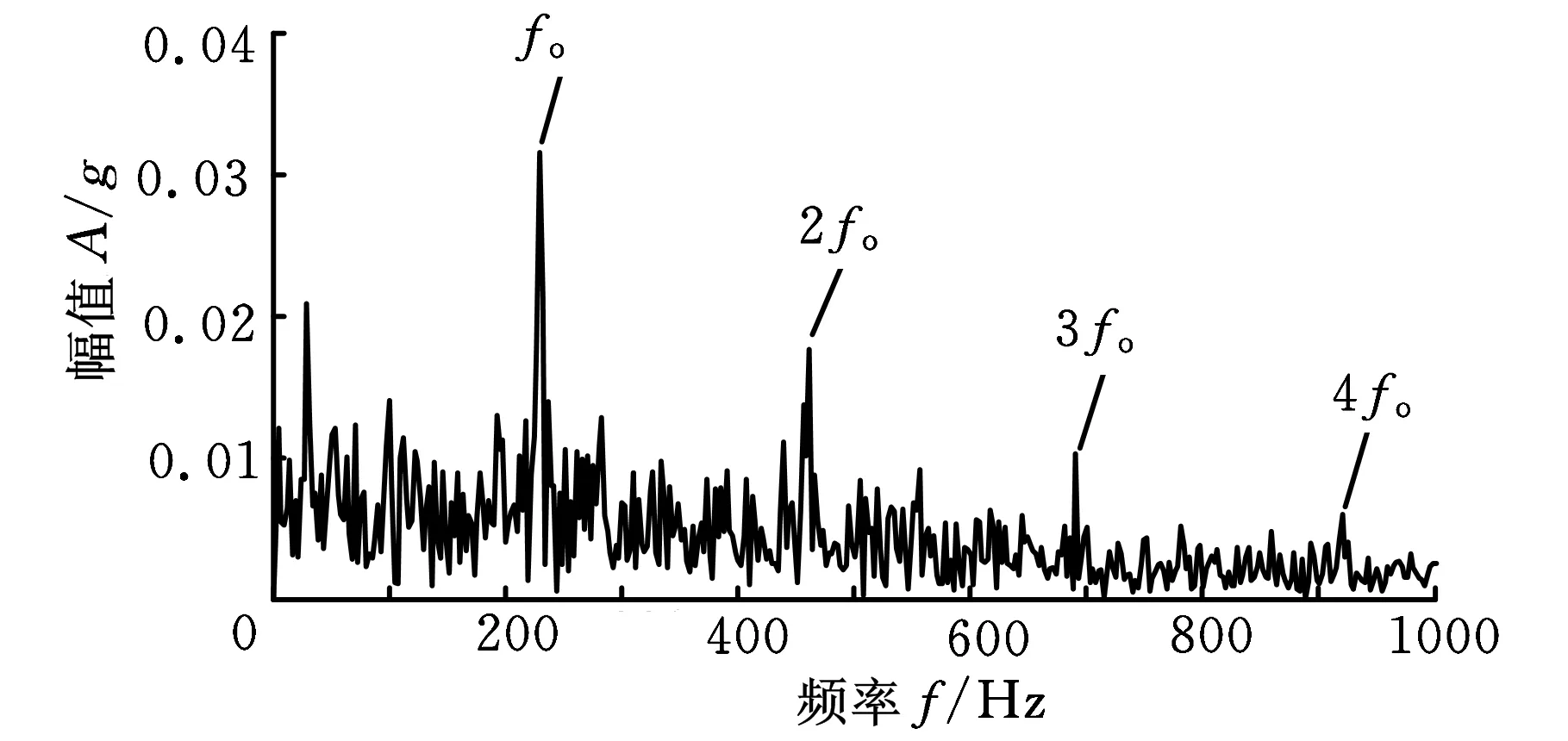
(c)解卷积信号的包络谱图8　本文提出方法的实测信号分析结果

为进一步验证基于包络谱稀疏度和最大相关峭度解卷积的早期故障诊断方法的优势,利用文献[5]中基于EMD降噪和谱峭度的轴承早期故障诊断方法对实测信号进行分析,结果如图9所示。图9a为EMD降噪后得到的信号，通过计算降噪信号的快速峭度图(结果如图9b所示)获得最佳带通滤波中心及滤波带宽，对滤波信号作包络谱分析，结果如图9c所示，图中没有出现任何频率尖峰，无法提取出故障特征频率信息。图10是利用文献[6]中基于最小熵解卷积的轴承微弱故障特征提取方法对原信号进行分析得到的结果，图10b中仅外圈特征频率2倍频和3倍频处谱线幅值偏高，但是峰值不够突出，诊断效果与本文方法相比差距明显。滚动轴承全寿命周期加速试验数据对比分析结果表明，本文所述方法在实际轴承诊断应用中具有一定优势，能够有效提取出早期故障阶段的微弱特征信息。

5　结语

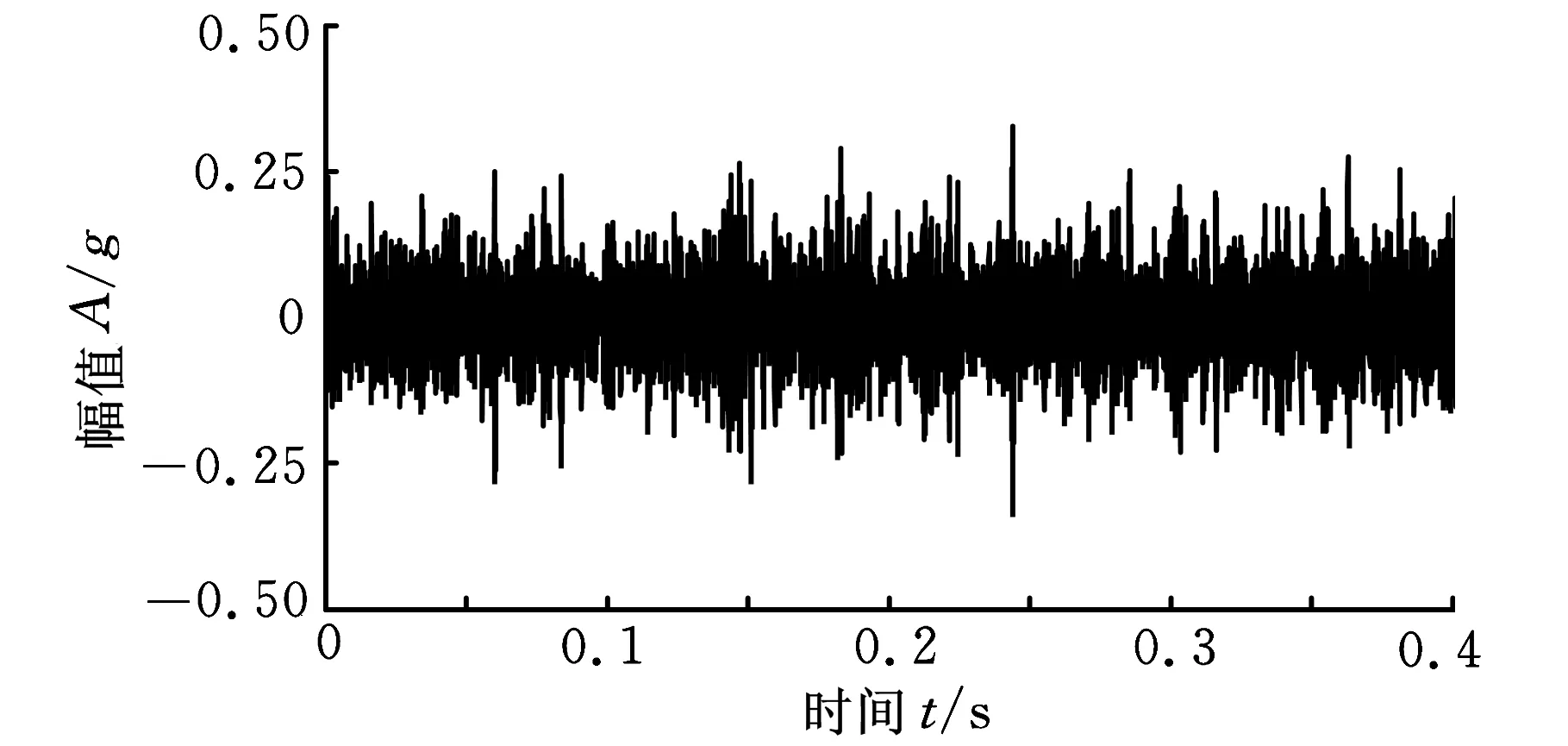
(a)EMD降噪信号

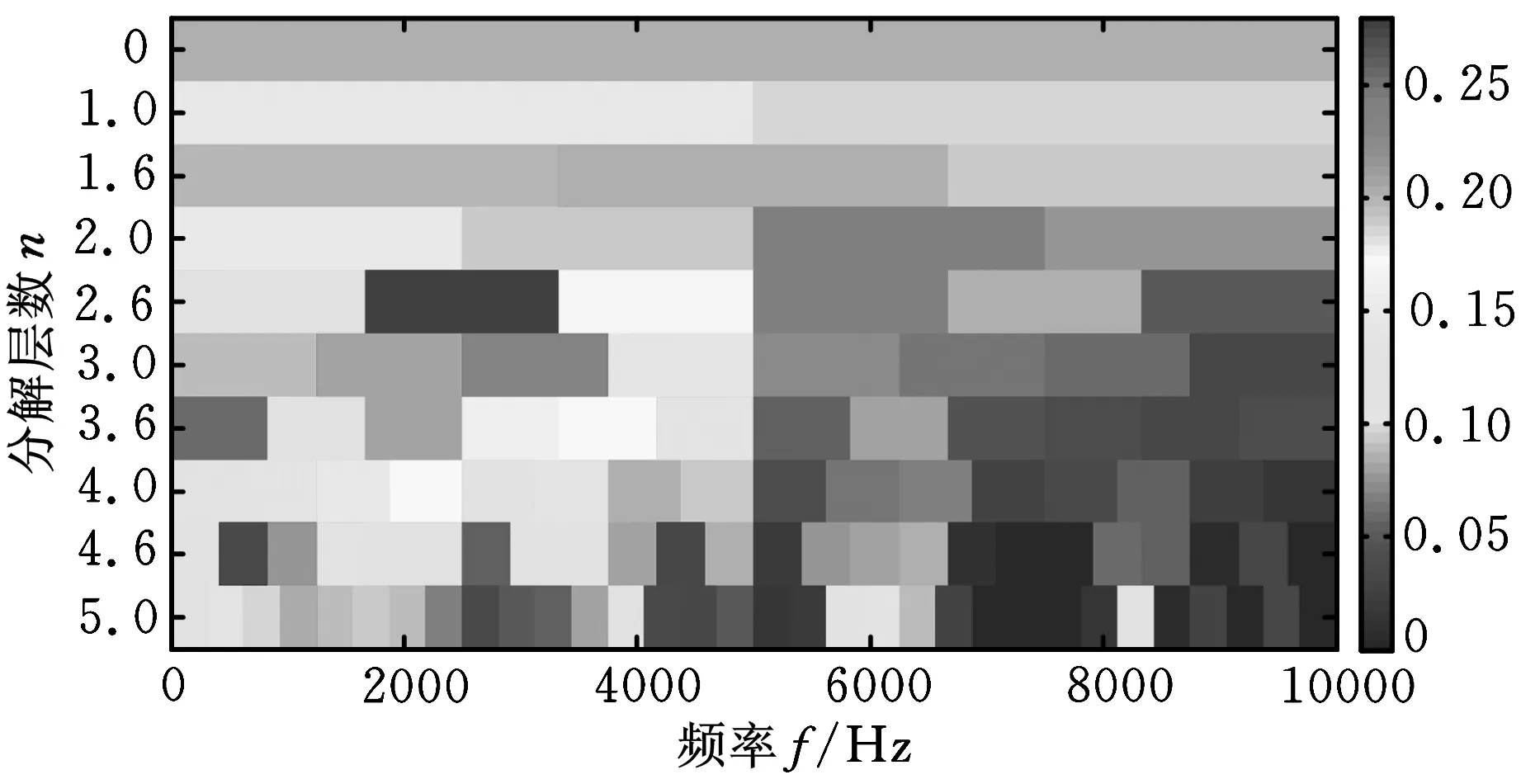
(b)降噪信号的快速峭度图

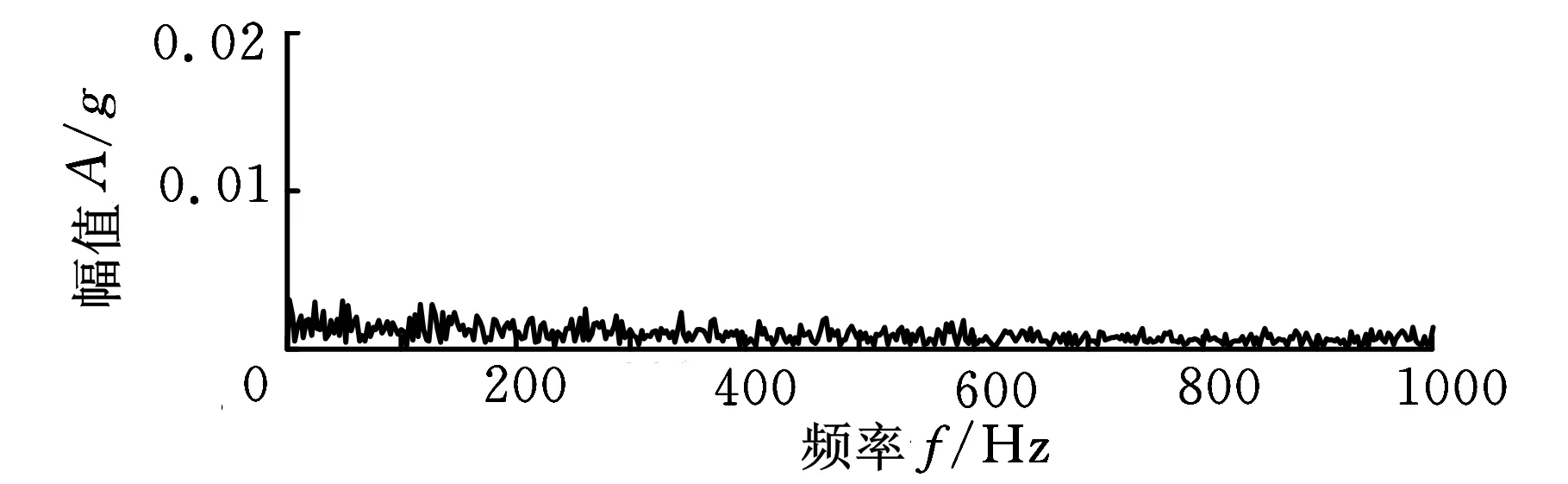
(c)滤波信号的包络谱图9　基于EMD降噪和谱峭度的实测信号分析结果

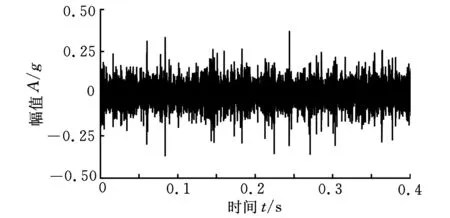
(a)最小熵解卷积信号

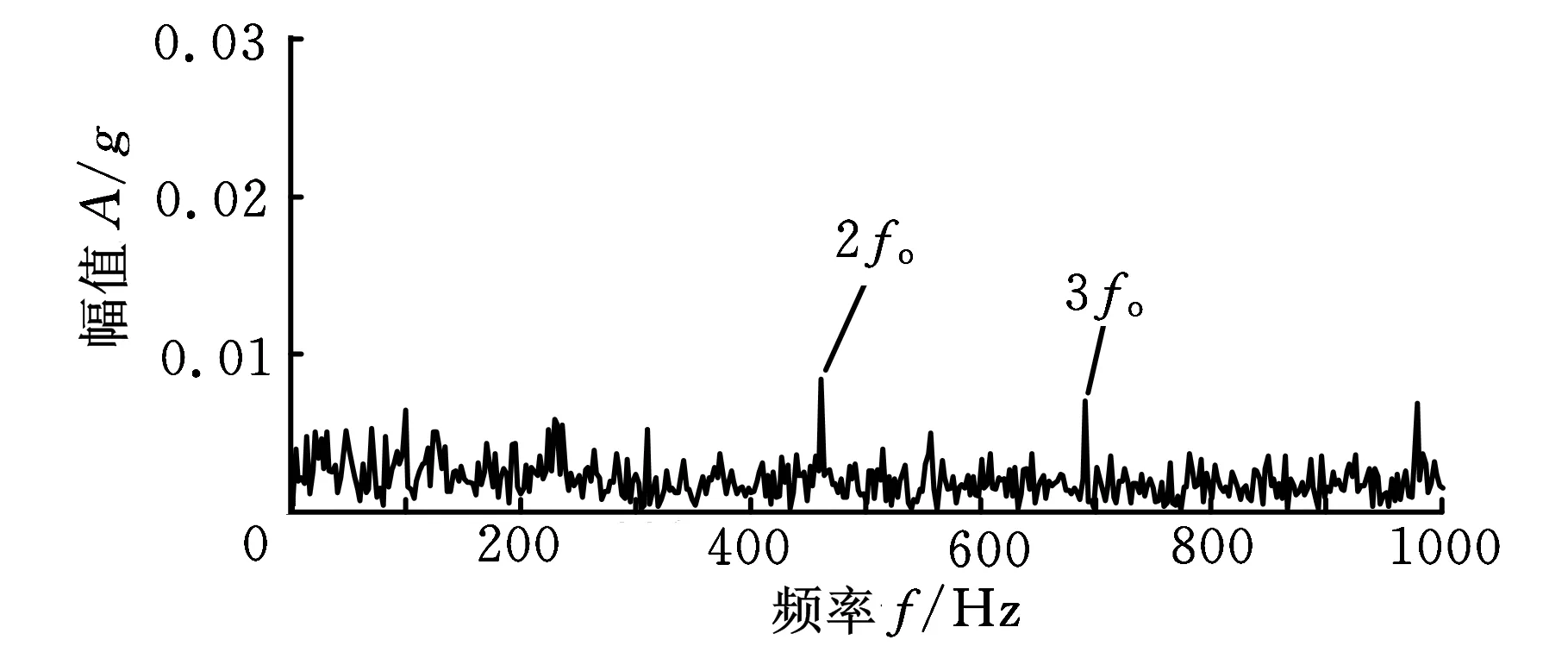
(b)解卷积信号的包络谱图10　基于最小熵解卷积的实测信号分析结果

本文提出了基于包络谱稀疏度和最大相关峭度解卷积的滚动轴承早期故障诊断方法,仿真和试验信号分析表明,该方法具有一定准确性和可靠性。笔者提出利用包络谱稀疏度指标来筛选最佳解卷积周期参数，旨在起到一个抛砖引玉的效果。

[1]赵志宏,杨绍普,李韶华.基于Hilbert谱奇异值的轴承故障诊断[J].中国机械工程,2013,24(3):346-350.

Zhao Zhihong,Yang Shaopu,Li Shaohua.Bearing Fault Diagnosis Based on Hilbert Spectrum and Singular Value Decomposition[J].China Mechanical Engineering,2013,24(3):346-350.

[2]曾庆虎,邱静,刘冠军,等.基于小波相关滤波-包络分析的早期故障特征提取方法[J].仪器仪表学报,2008,29(4):729-933.

Zeng Qinghu,Qiu Jing,Liu Guanjun,et al.Approach to Extraction of Incipient Fault Features Based on Wavelet Correlation Filter and Envelope Analysis[J].Chinese Journal of Scientific Instrument,2008,29(4):729-933.

[3]崔玲丽,康晨晖,胥永刚,等.滚动轴承早期冲击性故障特征提取的综合算法研究[J].仪器仪表学报,2010,31(11):2422-2427.

Cui Lingli,Kang Chenhui,Xu Yonggang,et al.Integrated Algorithm Research on Early Inpactive Fault Feature Extraction of Rolling Bearings[J].Chinese Journal of Scientific Instrument,2010,31(11)：2422-2427.

[4]莫代一,崔玲丽,王婧.基于双重Q因子的稀疏分解法在滚动轴承早期故障诊断中的应用[J].机械工程学报,2013,49(9):37-41.

Mo Daiyi,Cui Lingli,Wang Jing.Sparse Signal Decomposition Method Based on the Dual Q-factor and Its Application to Rolling Bearing Early Fault Diagnosis[J].Journal of Mechanical Engineering,2013,49(9):37-41.

[5]苏文胜,王奉涛,张志新,等.EMD降噪和谱峭度法在滚动轴承早期故障诊断中的应用[J].振动与冲击,2010,29(3):18-21.

Su Wensheng,Wang Fengtao,Zhang Zhixin,et al.Application of EMD Denoising and Spectral Kurtosis in Early Diagnosis of Rolling Element Bearings[J].Journal of Vibration and Shock,2010,29(3):18-21.

[6]Jiang Ruilong,Chen Jin,Dong Guangming,et al.The Weak Fault Diagnosis and Condition Monitoring of Rolling Element Bearing Using Minimum Entropy Deconvolution and Envelop Spectrum[J].Engineering Science Engineers,Part C:Journal of Mechanical Engineering Science,2013,227(5):1116-1129.

[7]江瑞龙.基于最小熵解卷积的滚动轴承故障诊断研究[D].上海：上海交通大学,2013.

[8]McDonald G L,Zhao Qing,Zuo M J.Maximum Correlated Kurtosis Deconvolution and Application on Gear Tooth Chip Fault Detection[J].Mechanical Systems and Signal Processing,2012,33:237-255.

[9]Tse P W,Wang Dong.The Design of a New Sparsogram for Fast Bearing Fault Diagnosis:Part 1 of the Two Related Manuscripts that Have a Joint Title as “Two Automatic Vibration-based Fault Diagnostic Methods Using the Novel Sparsity Measurement-Parts 1 and 2”[J].Mechanical Systems and Signal Processing,2013,40:499-519.

[10]Qiu Hai,Lee J,Lin Jing,et al.Wavelet Filter-based Weak Signature Detection Method and Its Application on Rolling Element Bearing Prognostics[J].Journal of Sound and Vibration,2006,289:1066-1090.

(编辑袁兴玲)

Diagnosis Method for Rolling Bearing Incipient Faults Based on Sparsity of Envelope Spectrum and Maximum Correlated Kurtosis Deconvolution

Tang GuijiWang Xiaolong

North China Electric Power University,Baoding,Hebei,071000

Early fault features of rolling bearings are very weak and are affected by environment noise seriously,so it is difficult to draw fault features.Aiming at solving this problem,MCKD was tried to diagnose faults for bearings,and sparsity of envelope spectrum was used to select the optimal deconvolution period parameter,then incipient fault diagnosis method for rolling bearings was proposed based on sparsity of envelope spectrum and MCKD.MCKD method corresponding to the optimal parameter was used to process the original signals and the envelope spectrum of deconvolution signals was obtained,the bearing faults were judged by analyzing the envelope spectrum.Simulated incipient fault signals and full lifetime datasets of rolling bearings were used to examine the feasibility of this method and the results show the new method can be applied to diagnose the incipient fault effectively.

rolling bearing;sparsity;maximum correlated kurtosis deconvolution(MCKD);fault diagnosis

2014-02-17

中央高校基本科研业务费专项资金资助项目(13QN49);河北省自然科学基金资助项目(E2014502052)

TH133.3；TH17< class="emphasis_italic">DOI

：10.3969/j.issn.1004-132X.2015.11.006

唐贵基,男,1962年生。华北电力大学能源动力与机械工程学院教授、博士研究生导师。主要研究方向为机械故障诊断与状态监测。王晓龙，男，1989年生。华北电力大学能源动力与机械工程学院博士研究生。