风力机定量泵-并联变量马达主传动系统并网控制
2015-10-29孔祥东
孔祥东 宋 豫 艾 超 王 静
1.先进锻压成形技术与科学教育部重点实验室(燕山大学),秦皇岛,066004 2.燕山大学河北省重型机械流体动力传输与控制实验室,秦皇岛,066004
风力机定量泵-并联变量马达主传动系统并网控制
孔祥东1,2宋豫1,2艾超1王静1,2
1.先进锻压成形技术与科学教育部重点实验室(燕山大学),秦皇岛,066004 2.燕山大学河北省重型机械流体动力传输与控制实验室,秦皇岛,066004
提出了液压型风力发电机组定量泵-双并联变量马达主传动系统并网的控制方法,即当首台变量马达处于并网状态时采用恒压控制方法实现下一台变量马达启动时系统不失稳,并采用结构不变性原理对双并联变量马达速度耦合进行解耦,当下一台变量马达启动后采用转速控制方法实现并网同步转速控制;建立了系统并网控制的数学模型,并进行了仿真研究,得到了不同风速(定量泵转速)条件下系统采用压力与转速控制的并网过程中定量泵转速、变量马达斜盘摆角、变量马达转速、系统高压压力的响应特性,验证了定量泵-双并联变量马达系统并网控制方法的有效性,为拓展液压型风力发电机组在大型及超大型机型中的应用奠定了理论基础。
风力发电;定量泵-并联变量马达;并网控制;压力控制;转速控制
0 引言
随着传统能源储量的急剧减少,人们对新能源的关注与研究正在不断地深入。风能作为洁净的可再生能源的一种,已经受到很多国家的重视,风电产业正在飞速发展。风中蕴含着用之不尽的能源,但是,目前风电行业面临着一个重要的问题是并网困难,主要是由于风力发电机组的电能质量不能满足电网要求,这就导致装机容量与发电量之间存在巨大的差距,设备不能发挥其能力。传统的风力发电机组机型主要是双馈型和直驱型,双馈型通过齿轮箱给主轴升速从而带动交流异步电动机,直驱机型风轮主轴直接与永磁同步发电机相连,两种机型最大的问题是传动系统无法消除风速波动对电能质量的影响。新型的液压型风力发电机组应用了液压系统无级调速与功率密度高的优势,有效降低功率波动的同时还减小了机组的重量,降低了装机成本,是未来风电发展的一种主要机型。2009年,苏格兰Artemis Intelligent Power公司采用数字定量泵-并联数字变量马达传动形式,进行了1.5MW液压型风力发电机组模型研究[1]。2010年,德国亚琛工业大学采用径向柱塞泵和轴向柱塞马达系统,搭建定量泵-并联变量马达实验系统,对其运行特性进行了实验研究[2-3]。但以上研究均未见应用的相关报道,没有实现产业化。
采用定量泵-并联变量马达系统作为风力发电机组动力传输机构,能够有效地提升机组的性能。研究者针对定量泵-并联变量马达系统进行了广泛的研究。文献[4]在定量泵-并联变量马达系统中采用压力规划法降低系统压力波动,同时在转速控制中加入扰动观测器,提高了系统的抗干扰能力和稳态精度;文献[5]对单泵多并联马达系统进行分层协调控制,根据一阶滑模观测器估算的道路条件确定最优滑移率,实现车辆优越的加速和减速性能;文献[6]针对越野性能要求高的步兵战车驱动系统,结合恒压网络技术提出改进的MRAC(Narendra model reference adaptive control)方法实现双马达速度同步控制,降低了压力波动,对负载干扰具有较强的鲁棒性;文献[7]分析了单变量泵并联变量马达的同步转速控制,利用基于流量均衡控制与压力速度之和反馈相结合的控制策略,无需解耦即可实现工程车辆同步控制。
本文以液压型风力发电机组主传动系统作为研究对象,采用定量泵-双并联变量马达系统实现并网控制。提出了基于系统恒压控制[8-10]的双并联变量马达转速控制[11-13]方法,有效解决了双并联变量马达启动时对系统的压力冲击问题,使同步发电机满足并网要求。
1 液压型风力发电机组工作原理
液压型风力发电机组定量泵-双并联变量马达主传动系统原理如图1所示,主要由风力机、定量泵-双并联变量马达液压系统、同步发电机组成。

图1 液压型风力发电机组主传动系统原理图
风力机吸收风能并传递至定量泵,定量泵输出高压油带动变量马达旋转,变量马达带动同步发电机将液压能转化为电能送入电网。
为了提高系统的效率与风能利用率,在风速低于双发电机并网阈值时,系统只投入一台变量马达及与其相连的发电机,当风速高于这一阈值时,开关阀打开,系统投入第二台变量马达及与其相连的发电机,实现双并联发电机发电。
2 定量泵-双并联变量马达系统数学模型
液压型风力发电机组定量泵-双并联变量马达主传动系统回路原理简图见图2。
采用图2所示的原理图模型推导定量泵-双并联变量马达系统传递函数时,两台变量马达型号相同,故其数学表达相同,以下角标1和2区别,并作如下假设:①连接管道为硬管且长度很短;②液压泵和马达腔的容积为常数;③系统中高低压腔的压力分别均匀相等;④不考虑补油系统。
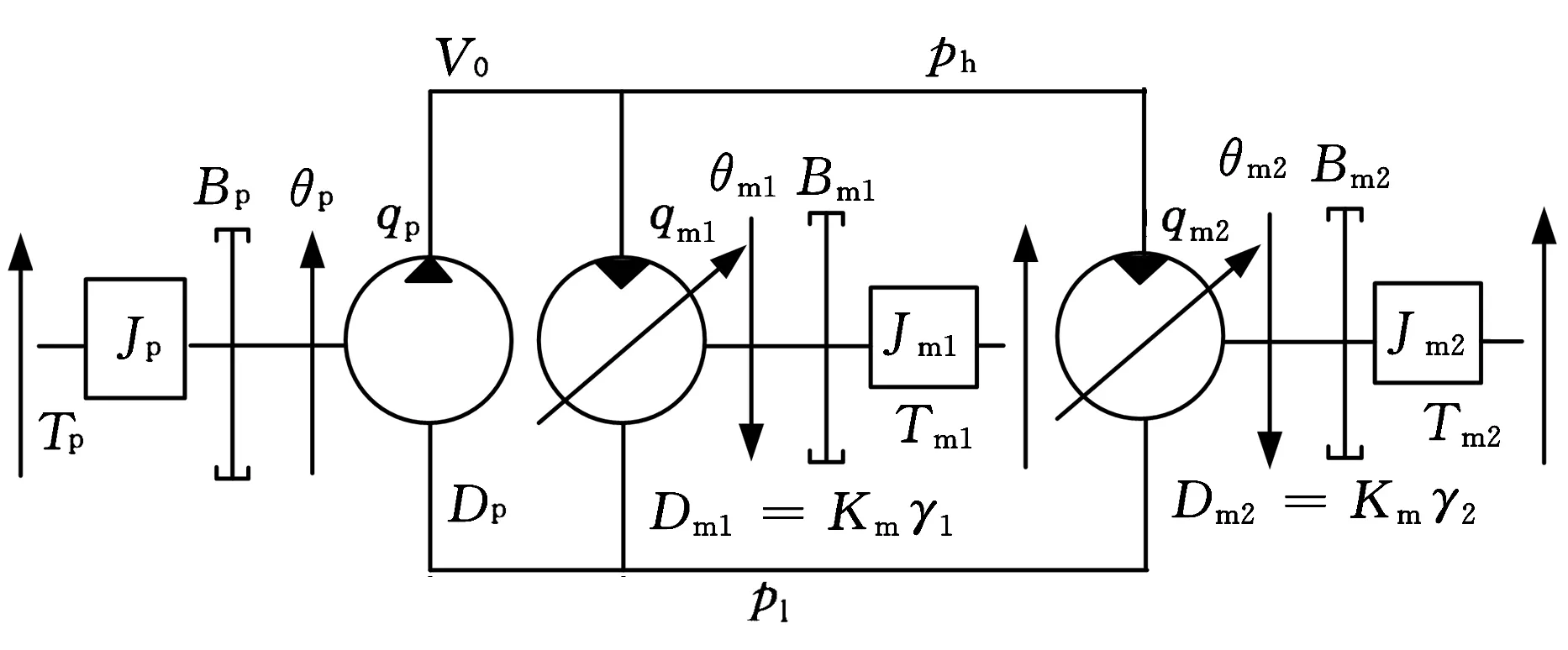
图2 定量泵-双并联变量马达主传动系统回路原理简图
在工作点处将斜盘摆角γ与高压管路压力ph的乘积构成一个非线性方程进行线性化处理,有
γph=(γ(0)+Δγ(t))(ph(0)+Δph(t))
(1)
式中,γ为变量马达斜盘摆角,为[0,1]区间取值的量纲一数值;γ(0)为变量马达初始斜盘摆角,rad;Δγ(t)为变量马达初始斜盘摆角变化量,rad;ph(0)为高压管路初始压力,Pa;Δph(t)为高压管路压力变化量,Pa。
忽略二阶无穷小量,整理得
γph=γ0ph0+Δγ(t)ph0+γ0Δph(t)
(2)
式中,ph0为高压管路初始压力,Pa;γ0为变量马达初始斜盘摆角,rad。
变量马达与负载的力矩平衡方程的拉氏变换式为
Kmγph0+Kmγ0ph=Jms2θm+Bmsθm+Gmθm+Tm
(3)
式中,Km为变量马达排量梯度,m3/rad;θm为变量马达转角,rad;Jm为变量马达与负载(折算到变量马达轴上)的总惯量,kg·m2;Bm为变量马达轴端的黏性阻尼系数,N·s/m;Gm为变量马达轴端的负载弹簧刚度,N/m;Tm为作用在变量马达上的电磁转矩,N·m。
定量泵-双并联变量马达高压腔流量连续性方程为
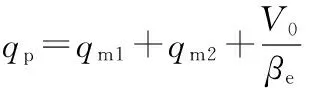
(4)
式中,qp为定量泵流量,m3/s;qm为变量马达流量,m3/s;V0为定量泵与变量马达之间高压管路总容积,m3;βe为油液综合体积弹性模量,Pa。
将变量马达流量方程代入式(4)有
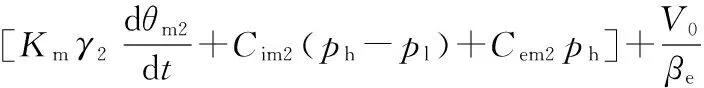
(5)
式中,pl为低压管路压力,Pa;Cim、Cem分别为变量马达内外泄漏系数,m3/(s·Pa)。
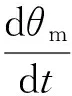
(6)
式中,ωm0为变量马达转速初始值,rad/s;Δωm(t)为变量马达转速变化值,rad/s。
将式(6)代入式(5),则其拉氏变换式为
qp=(Kmγ1ωm01+Kmγ01sθm1)+
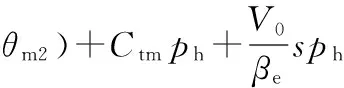
(7)
式中,Ctm为变量马达总泄漏系数,Ctm=Cim+Cem。
由变量马达流量方程与式(4)、式(7)得到定量泵-双并联变量马达系统传递函数为
qm1=Dm1ωm1+Cim1(ph-pl)+Cem1ph
(8)
qm2=Dm2ωm2+Cim2(ph-pl)+Cem2ph
(9)
Kmγ1ph0+Kmγ01ph=Jm1s2θm1+Bm1sθm1+Gm1θm1+Tm1
(10)
Kmγ2ph0+Kmγ02ph=Jm2s2θm2+Bm2sθm2+Gm2θm2+Tm2
(11)
qp=Kmγ1ωm01+Kmγ01sθm1+Kmγ2ωm02+
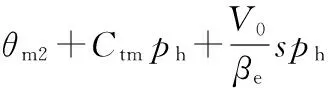
(12)
由定量泵流量方程和式(8)~式(12),联立可得定量泵-双并联变量马达系统传递函数方框图,见图3。
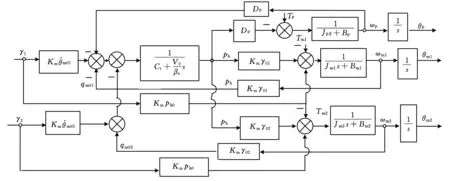
图3 定量泵-双并联变量马达系统方框图
当定量泵和两变量马达输出端刚度很大时,Gm1=Gm2=Gp=0。图3中共包含5个输入量γ1、γ2、Tp、Tm1、Tm2和3个输出量θp、θm1、θm2,系统高压压力ph为中间变量。
由式(11)得
ph=
(13)
式中,ωp为定量泵转速,rad/s;Dp为定量泵排量,m3/rad;Ct为总泄漏系数,即定量泵总泄漏系数与变量马达总泄漏系数之和,m3/(s·Pa)。
将式(13)代入定量泵力矩平衡方程得
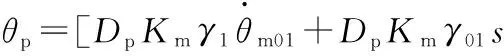
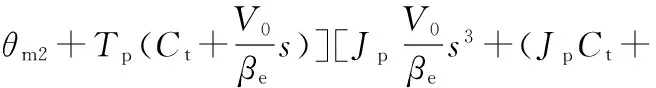
(14)
式中,θp为定量泵转角,rad;Tp为作用在定量泵上的驱动力矩,N·m;Jp为定量泵和负载(折算到定量泵轴上)的总惯量,kg·m2;Bp为定量泵轴端的黏性阻尼系数,N·s/m;Gp为定量泵轴端的负载弹簧刚度,N/m。
3 定量泵-双并联变量马达系统并网控制策略
3.1并网控制器设计思想
当变量马达1工作于并网状态、变量马达2未启动时,根据管道中流量平衡的原理,检测定量泵转速可以给定变量马达斜盘摆角,即在恒流状态下给定变量马达1斜盘摆角基准值。
当变量马达1工作于并网状态、变量马达2启动时,检测风速信号和定量泵转速信号,送入压力给定控制器,其输出与系统实际压力信号的差值送入压力控制器,控制变量马达1斜盘摆角进行调整,实现系统高压压力基本稳定在给定值,即在恒压状态下进行变量马达2启动。定量泵转速受变量马达1斜盘摆角与变量马达2斜盘摆角的共同作用,当定量泵输入转速为定值时,可采用结构不变性解耦原理,实现系统转速控制环节互不相关,即变量马达2斜盘摆角和转速变化均不会影响系统高压压力,系统压力只由变量马达1斜盘摆角决定,通过变量马达1摆角控制器控制,实现系统高压压力恒定。
当变量马达1工作于并网状态、变量马达2启动、系统工作于恒压状态时,系统稳定于(1500±6)r/min的并网同步转速下,实现变量马达2进入并网工作状态。
3.2并网控制器设计
根据图4所示的并网流程,可实现定量泵-双并联变量马达系统并网控制器的设计,但是,由式(13)分析可知,无论变量马达1斜盘摆角、变量马达2斜盘摆角、变量马达2外负载中哪一参量改变,都会引起系统高压压力变化,即两转速控制通道相互耦合。
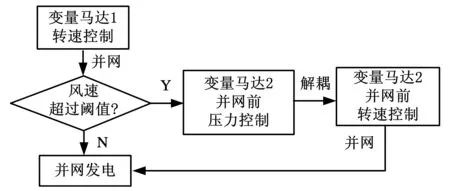
图4 定量泵-双并联变量马达系统并网流程图
变量马达在调整转速过程中,由于风力机转动惯量很大对其转速的影响不大,故可以认为定量泵转速不变;变量马达1处于并网状态时,其转速被电网拖住为定值,化简定量泵-双并联变量马达系统传递函数,其简化方框图见图5。
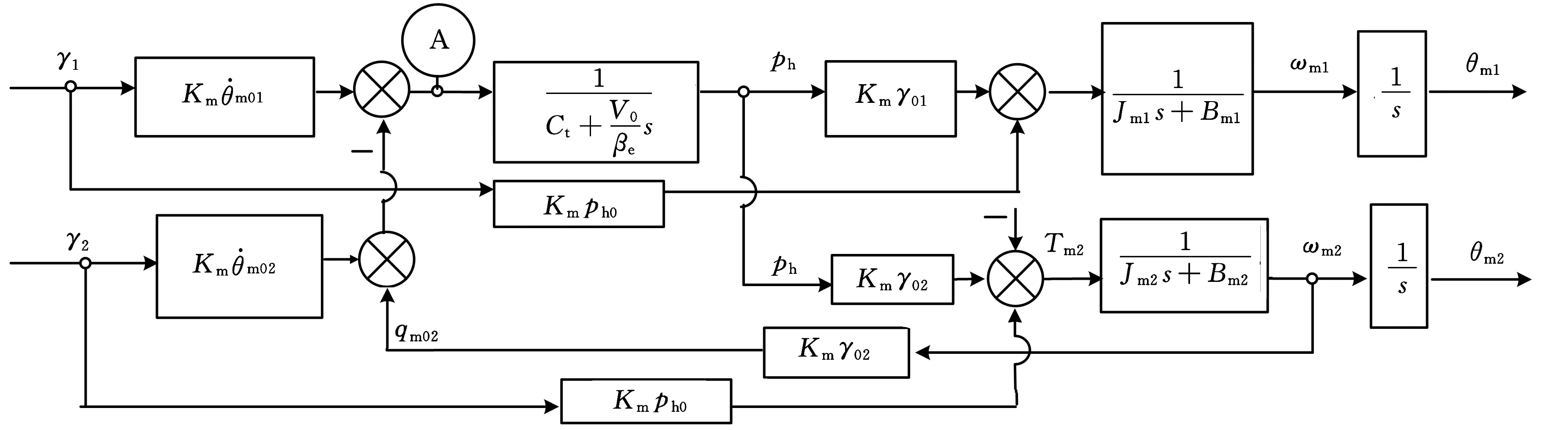
图5 定量泵-双并联变量马达系统简化方框图
分析图5可知,若要保证高压压力不变,则需令A点流量不变,而A点流量变化受变量马达1和变量马达2两部分变化影响:
(15)
(16)
式中,Δqm1、Δqm2分别为变量马达1、2引起的A点流量变化,m3/s。
由A点流量不变的要求得
ΔqA=Δqm1+Δqm2=0
(17)
式中,ΔqA为A点流量变化,m3/s。
由式(15)~式(17)联立得
(18)
由式(18)可以看出,通过实时检测变量马达2斜盘摆角和变量马达2转速的变化值,即可计算出变量马达1斜盘摆角的补偿值送入控制器,在此利用结构不变性解耦补偿方法实现了系统恒压控制。
基于以上分析可以得出定量泵-双并联变量马达控制系统简图见图6,系统共包括5个控制器:压力给定控制器、压力控制器、变量马达1斜盘摆角控制器、变量马达2斜盘摆角控制器、斜盘摆角补偿控制器。
通过上述理论分析,该方法可扩展到定量泵-多并联变量马达系统,实现多台发电机依次并网,从而拓展液压型风力发电机组在大型及超大型机型中的应用。

图6 定量泵-双并联变量马达控制系统简图
4 定量泵-双并联变量马达系统并网控制仿真研究
4.1仿真平台
利用AMESim与MATLAB/Simulink软件搭建了液压型风力发电机组定量泵-双并联变量马达主传动液压控制系统仿真模型,如图7所示,采用该模型对不同风速变化条件下高压压力、变量马达斜盘摆角、变量马达转速响应特性进行了分析。
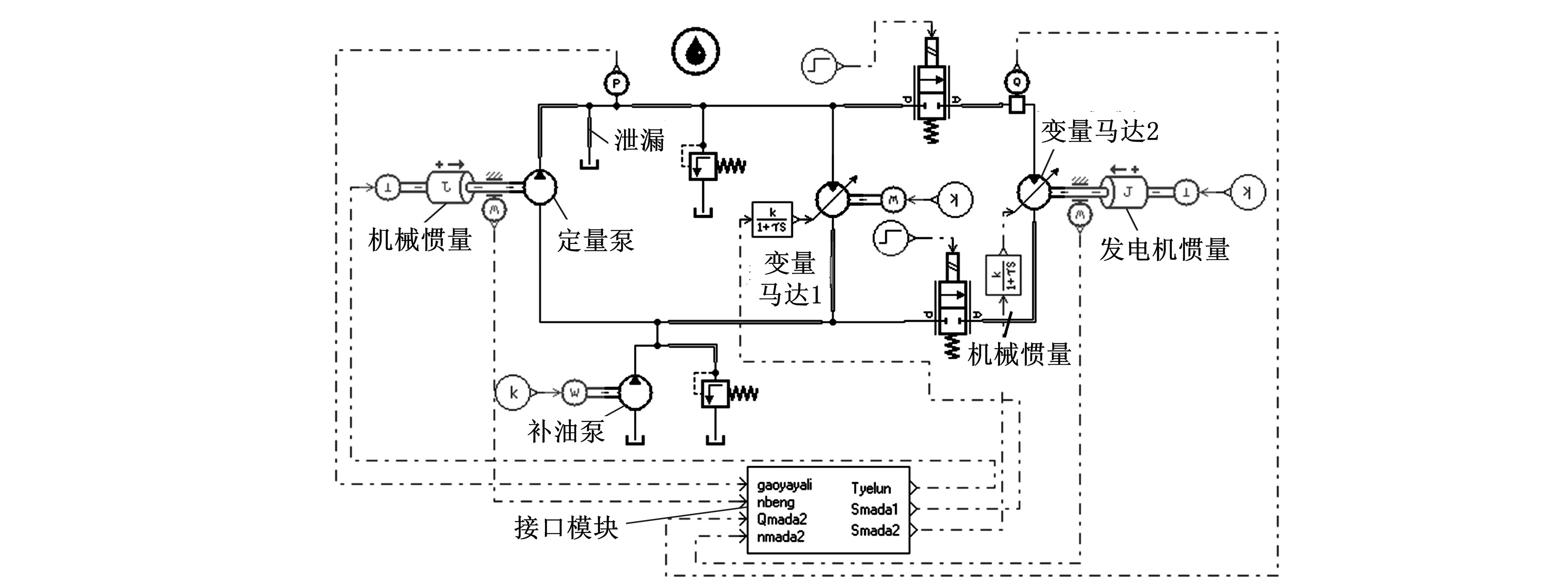
图7 液压控制系统仿真模型
针对液压型风力发电机组设置主传动液压系统仿真参数如表1所示。
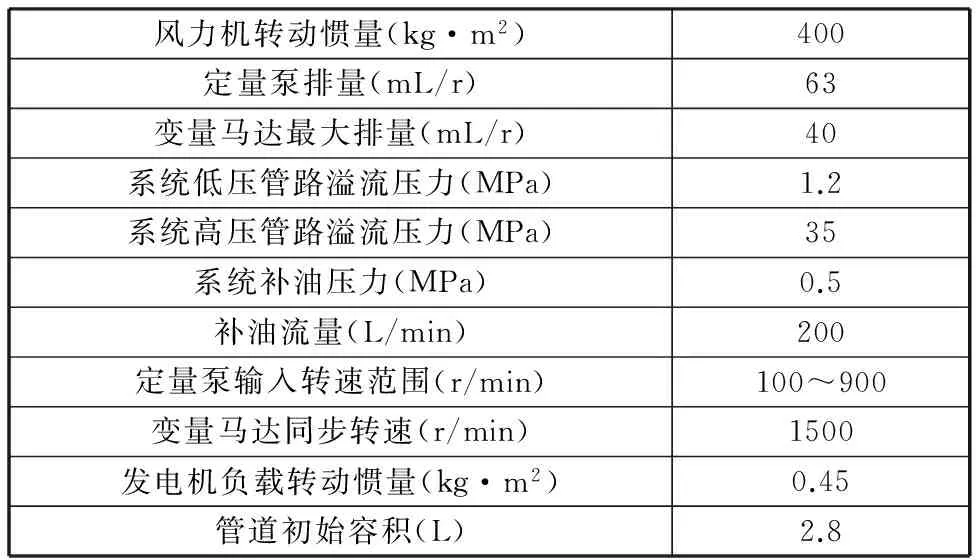
表1 主传动液压系统仿真参数表
风力机大部分时间工作在局部负荷区,通过实时检测风速,并从风力机气动转矩特性获取风功率值,便可计算出系统高压压力给定值。
对于液压型风力发电机组,风速取值范围为4~13 m/s。当并联变量马达处于并网状态且风速不变时,计算得出系统高压压力给定值如表2所示。

表2 高压压力参数设定
4.2仿真结果分析
图8所示为风速9 m/s时变量马达2进入并网状态前系统响应仿真结果。在第10s将变量马达2启动。
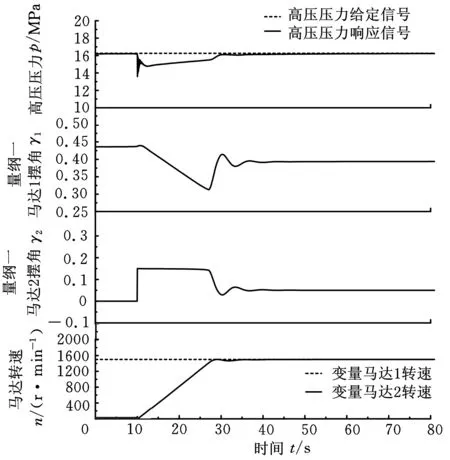
图8 风速9m/s时系统仿真结果
分析图8的结果可知,当风速(定量泵转速)不变,系统稳定于某一状态时,变量马达2进入并网状态前,变量马达1保持稳定的并网转速,变量马达2转速按要求提升至并网转速,并控制高压压力快速稳定于恒值,确保系统不失稳。
图9、图10所示为风速6~9 m/s斜坡变化、(8+0.5sint)m/s正弦变化时变量马达2进入并网状态前系统响应仿真结果。在第10s将变量马达2启动。

图9 风速6~9 m/s斜坡变化时仿真结果

图10 风速(8+0.5sint)m/s正弦变化时仿真结果
分析图9、图10的结果可知,当风速(定量泵转速)分别为斜坡变化、正弦变化时,解耦控制方法均可实现变量马达1在并网条件下、变量马达2进入并网状态前,对系统高压压力的稳定控制,保证变量马达2启动直至达到并网状态,系统高压压力在一定范围内波动,满足系统控制要求。
由图8~图10结果可以看出,当风速(定量泵转速)按照上述情况变化时,变量马达1能够在变量马达2启动时迅速调整斜盘摆角,满足并网的同步转速要求,并且两台变量马达能够快速跟踪风速变化使系统的高压压力在变化过程中均只有小幅波动并很快恢复稳定状态,保证并网对系统压力的控制要求。同时,变量马达2的转速逐渐升高并稳定到并网同步转速,此过程实质上就是定量泵流量的分流过程。仿真结果从理论上验证了定量泵-双并联变量马达系统并网控制方法的有效性。
5 结论
(1)对液压型风力发电机组定量泵-双并联变量马达系统的数学模型进行了分析,得到了第二台变量马达并网时,解决系统高压压力稳定控制的解耦控制方法,抑制了两台变量马达斜盘摆角变化时因互相耦合导致的系统高压压力波动。
(2)采用并网前系统恒压状态下并联马达恒转速控制策略,实现了并联两台变量马达的并网控制,可防止液压系统失稳,获得良好的控制效果,从而保证了双并联变量马达顺利达到并网要求。
[1]Tsutsumi K,Shimizu M,Maekawa A,et al.Power Generating Apparatus of Renewable Energy Type:US,20130067900[P].2011-12-1.
[2]Kohmäscher T.Modell Bildung Analyse und Auslegung Hydrostatischer Antriebsstrangkonzepte[D].Aachen,Germany:RWTH Achen,2008.
[3]Johannes S,Nils V,Hubertus M.Hydrostatic Drive Train in Wind Energy Plants[C]//EWEA 2011 Brussels Europe’s Premier Wind Energy Event Scientific,Proceedings European Wind Energy Conference & Exhibition.Brussels,2011:20-23.
[4]郑琦,李运华,杨丽曼.控并联变量马达速度系统复合控制策略[J],北京航空航天大学学报,2012,38(5):692-696.
Zheng Qi,Li Yunhua,Yang Liman.Compound Control Strategy for the Pump-controlled-parallel-variable-displacement-motor Speed System[J].Journal of Beijing University of Aeronautics and Astronautics,2012,38(5):692-696.
[5]Li Yunhua,He Liuyu,Yang Liman.Coordinated and Optimal Acceleration and Deceleration Driving Control for Multi-axle Hydrostatic Driving Vehicle [C]//12th International Conference on Control,Automation,Robotics and Vision.Guangzhou,2012:524-529.
[6]Wu Baolin, Qiu Lihua, Wang Zhanlin.Four Wheels Driven Independently by One Pump Drlving Four Hydraullc Motors[J].Chinese Journal of Mechanical Engineering,2005,18(2):232-236.
[7]吴保林,裘丽华,唐志勇,等.工程机械液压底盘模拟实验台双马达同步技术研究[J].中国机械工程,2006,17(9):899-902.
Wu Baolin,Qiu Lihua,Tang Zhiyong,et al.Research on Speed Synchronization Control of Double Motors of Hydraulic Chassis Simulation Experimental Device of Engineering Vehicles[J]. China Mechanical Engineering,2006,17(9):899-902.[8]Schachles C,Schachles P,Schachles E,et al.Wind Power Generating System:US,4503673[P].1979-05-25.[9]David M,Tracy C.Hydraulic Control Device for Wind Turbine:US,4715782[P].1998-10-29.
[10]查普驱动公司.涡轮机速度稳定控制系统:中国,200980136335.3[P].2010-03-25.
[11]Ding Haigang,Zhao Jiyun.Characteristic Analysis of Pump Controlled Motor Speed Servo in the Hydraulic Hoister[J].International Journal of Modelling, Identification and Control,2013,19(1):64-74.[12]Triet Hung Ho,Kyoung Kwan Ahn.Design and Control of a Closed-loop Hydraulic Energy-regenerative System[J].Automation in Construction,2012,22:444-458.
[13]白国长,祁晓野,王占林.具有相乘非线性的马达速度鲁棒控制[J],北京航空航天大学学报,2008,34(7):803-806.
Bai Guochang,Qi Xiaoye,Wang Zhanlin.Motor Speed Robust Control with Multiplying Nonlinear Property[J].Journal of Beijing University of Aeronautics and Astronautics,2008,34(7):803-806.
(编辑苏卫国)
Grid Connected Control in Fixed Displacement Pump-Parallel Variable Motor of Main Transmission System in Wind Turbine
Kong Xiangdong1,2Song Yu1,2Ai Chao1,2Wang Jing1,2
1.Key Laboratory of Advanced Forging & Stamping Technology and Science(Yanshan University), Ministry of Education of China,Qinhuangdao,Hebei,066004 2.Hebei Provincial Key Laboratory of Heavy Machinery Fluid Power Transmission and Control,Yanshan University,Qinhuangdao,Hebei,066004
A grid connected control method was presented herein,which was used in the main transmission system of the fixed displacement pump-double parallel variable motor in hydraulic wind turbine,namely when the first variable motor worked in the state of grid connected,another variable motor didn’t lose stability in startup under the constant pressure control method.The rotate speed coupling of the double parallel variable motor was eliminated with the principle of structure invariance,therefore,when another variable motor was post-launch,the grid connected synchronous rotate speed was controlled under the speed control method.Meanwhile,the grid connected control mathematical model was established,and simulation was conducted.With pressure and speed control,the fixed displacement pump rotate speed,the variable motor swashplate angle,the variable motor rotate speed and the system high pressure response characteristics in the process of grid connected were obtained under the condition of different wind speed (fixed-displacement pump rotate speed).The grid connected control method was verified in the fixed displacement pump-double parallel variable motor.This reserach lays a theoretical foundation to expand the hydraulic wind turbine in the applications of large and super large wind turbine.
wind power generation;fixed displacement pump-parallel variable motor; grid connected control; pressure control; speed control
2015-03-15
国家自然科学基金资助项目(51475406;51405423;51375422)
TH137DOI:10.3969/j.issn.1004-132X.2015.16.015
孔祥东,男,1959年生。燕山大学机械工程学院教授、博士研究生导师。主要研究方向为流体传动及控制、液压型风力发电机组等。发表论文180余篇。宋豫,男,1986年生。燕山大学机械工程学院博士研究生。艾超,男,1982年生。燕山大学机械工程学院讲师、硕士研究生导师。王静,女,1987年生。燕山大学机械工程学院硕士研究生。
