面向汽车投产排序的混合多目标网格遗传算法

唐秋华　胡　进　张利平　操小军

1.武汉科技大学,武汉,430081　　2.神龙汽车公司技术中心,武汉,430056

面向汽车投产排序的混合多目标网格遗传算法

唐秋华1胡进1张利平1操小军2

1.武汉科技大学,武汉,4300812.神龙汽车公司技术中心,武汉,430056

汽车投产排序时，希望同时实现零部件消耗均衡化、车型调整费用最小化、工位作业位置精准化三个目标，为此提出一种基于Pareto层级的混合多目标网格遗传算法(HmoGA)。先将个体排斥机制加入到Pareto层级构造中，使非支配解的分布更均匀,再融合Pareto层级划分、网格拥挤度评价与相邻个体几何距离计算，设计一种多目标自适应网格选择机制，用于从动态变化的父代种群中选择较优个体构成进化种群、获取交叉运算的父代基因、改善非支配解集的分布质量。混合双基因位的迁移算子对非支配解进行邻域搜索，适时扩大搜索空间，跳出局部最优。利用三组不同规模的测试问题集,从非支配率、非支配解数量和相邻个体距离偏差三个指标方面进行比较,实验证明HmoGA算法在收敛性、解的数量和分布性方面都比NSGA-Ⅱ算法有显著优势。

Pareto层级；网格拥挤度;自适应选择;个体排斥机制；邻域搜索

0　引言

随着市场竞争的激烈化和客户需求的个性化,面向订单的多品种、小批量生产已逐步成为汽车等行业的主要生产模式。在其混流生产线上,多种产品的投产排序已经成为一个重要决策,它不仅影响到企业的效率和成本[1]，而且关系到产品交货期和客户满意度，推动着投产排序问题本身的演变，促其发展成为一种多目标优化问题。

解决多目标优化问题,应用最广泛的是多目标进化算法，如多目标遗传算法(MOGA)、非支配排序遗传算法(NSGA)等。MOGA利用遗传算法的精英保留机制，对所求出的非支配解进行继承。NSGA基于Pareto层级进行个体排序，选择最低层级(非支配解)或较低层级的个体进行遗传操作。上述经典算法中，普遍存在Pareto层级构造速度过慢、种群多样性差、搜索空间狭窄等问题。

为提高Pareto层级构造速度,Deb等[2]提出了改进型非支配排序遗传算法(NSGA-Ⅱ)，刘敏等[3]提出一种快速非支配排序算法,鲍培明等[4]使用了归一化排序非支配集构造方法。上述构造方法在一定程度上加快了Pareto排序,但仍缺乏非支配个体重复进入归档集的阻止机制，相同个体共同存在的可能性仍然很大,这对保持种群多样性不利，容易早熟。

种群多样性可有效防止算法陷入局部最优。为维护种群的多样性,杨虎等[5]将聚集密度方法应用到粒子群算法中，利用粒子群的强大搜索性能和科学的个体聚集度评价方式，使非支配解分布更加均匀。李志强等[6]将聚类方法加入到NSGA-Ⅱ中,弥补了三目标及三目标以上情形下非支配解分布性不足的缺陷。然而,上述算法对非支配解集和进化种群没有相应的调整策略，当所获得的非支配解数量大于进化种群规模时，无法科学地选择进入下一代的个体；当非支配解数量大于一定规模时,适应度评价所耗费的计算时间长，且难以持续达到理想的分布性。

拓展搜索空间是搜寻更多的非支配解和跳出局部最优的唯一途径。目前，扩大搜索空间的主要方法有变步长搜索、启发式搜索等。戚玉涛等[7]融合了启发式局部搜索策略和变步长搜索机制，在进化过程中，根据适应度随时进行步长调整,在保证全局优化的同时提高了局部搜索能力。贾宁等[8]结合启发式搜索和反馈修正机制增加了算法的搜索性能,使算法快速且有效地寻找较优的个体，最终确立了最佳的单路口交通控制方案。但对于装配线投产排序问题，变步长方式实现困难，而启发式搜索的搜索范围过小则可能缺乏效果，过大又造成优化复杂度过高，影响进化效率。

为克服上述算法存在的早熟、分布性不足、局部最优的缺点,本文在快速Pareto层级评价时加入相同个体排斥机制,利用相邻个体几何距离的大小来对非支配解进行筛选，运用2-opt邻域搜索机制对归档集进行邻域搜索，区别出相同目标值的非支配解,保持了非支配解的良好分布性，扩大了解空间的搜索性能。针对汽车投产排序问题，将所提出的算法与NSGA-Ⅱ进行了性能比较。

1　多目标投产排序问题

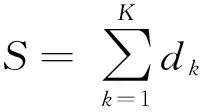
1.1前提假设及约束条件

假定混合流水装配线的运行满足以下前提条件:①传送带以恒定速度运行,且每个产品以固定生产节拍TC送到传送带进行生产;②各工作站j左右两侧均是开放的,工作站内工人允许超出工作站范围作业;③前一个工位的工人对一辆车操作完毕后,下一个工位的工人才能对这辆车进行装配;④以最小生产循环为单位，进行循环式生产;⑤最小循环单元内第一辆车在第一个工位的释放时间为0，则第一个工位的首个产品的装配时间为0。

基于上述假定，多车型混合流水生产投产排序问题可以概括为：将K种总数为S的汽车投入到由J个串行工位构成的生产线上，求最优投产序列，以达到所要求的目标。其约束条件如下：

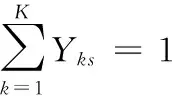
(1)

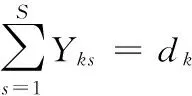
(2)

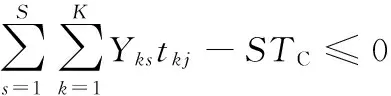
(3)

式中,tkj为车型k在工位j上的总操作时间，j∈{1，2,…,J}。

式(1)保证了在生产序列上每个位置有且仅有一辆车;式(2)保证每种车型的投产数量满足生产需求规定；式(3)保证在最小生产循环内,每个工位的有效工作时间小于总时间，不存在超负荷而无法完成的情况。

1.2多目标函数

在汽车投产排序时，决策者希望最终方案既满足市场需求，同时还能保持生产的稳定性。多目标优化是解决上述问题的有效方法，当前研究考虑以下三个目标：零部件消耗均衡化，车型调整费用最小化，工位作业位置精准化。

1.2.1零部件消耗均衡化

随着同时生产的车型数量增多，线边零部件的类型和数量剧增。在生产过程中，若线边零部件的消耗量发生变动，则必然增大线边物料存储压力。同时，上游零部件供应商、物料供应超市、物料配送人员的工作状态也忙闲不均。长此以往，必然造成生产现场的紊乱。为更好地利用有限的线边存储空间，在投产排序时，应促使物料消耗均衡化。其目标函数为

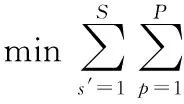
(4)

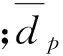
式(4)从生产过程出发，对投产序列中的每台车，控制其对各零件的实际消耗量与理论消耗量之间的偏差，促使零部件供应与消耗基本匹配,从而减小线边库存的压力。

1.2.2车型调整费用最小化

汽车制造从以往的单品种大批量生产已逐步发展成为多品种、小批量生产。不同产品类型间的切换，需要调整准备时间，还会产生价格不低的调整成本。例如，在涂装车间进行不同颜色间切换时，需更换和冲洗油漆喷头，造成喷漆效率降低、生产成本增高、环境污染加剧等后果。因此，控制产品类型的切换也成为投产排序时的一个重要目标：

(5)

式中,Cjkk′为工位j上从车型k变换到k′的调整费用。

1.2.3工位作业位置精准化

各台车按照固定生产节拍投放到生产线上，但在焊接、喷漆和装配车间，各工位的左右两边是开放的，相邻工位间无严格界限。因此，工人们可能会偏离自己工位，造成相邻工位间的干扰。故在投产排序时，尽量让各工位的工作位置精准化，减少拥挤或阻塞，避免生产的紊乱。

为解决以上问题,最小化投产序列中各车辆在每工位的完工时间与生产节拍之间的最大偏差[9],目标函数如下：

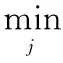
(6)

其中,fjs为j工位上第s辆车的装配终止时间,其值等于装配开始时间加上这辆车所需的装配时间，即

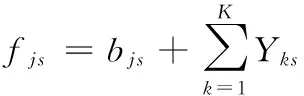
(7)

式中，bjs为j工位上第s辆车的装配开始时间。

在不同情形下利用如下公式计算bjs:

bjs=fj,s-1j=1,∀s∈{2,3,…,S}

(8)

bjs=fj,s-1s=1,∀j∈{2,3,…,J}

(9)

bjs=max(fj-1,s,fj,s-1)

∀j∈{2,3,…,J},s∈{2,3,…,S}

(10)

式(8)表明在第一个工位中，后一辆车的装配开始时间等于前一辆车的装配结束时间;式(9)表明各个工位的第一个产品的开始时间等于前一个工位在这个产品上的结束时间；式(10)表明某工位工人将当前车型操作完成之后，且前一个工位的工人对生产循环中的下一辆车操作完成之后，该工人才能对这辆车进行装配。

由式(6)可见,各工位的完工时间与生产节拍之间的最大偏差越小，各工位在有效工作位置内完成给定任务的比例越高，相邻工位间干扰的可能性就越小，操作也就越稳定。

2　多目标自适应网格选择机制

在最小生产循环单元内，不同车型按照投产序列依次进行生产，针对每个序列可得出上述三个目标值。不同于单目标优化，多目标问题不能单纯依据某个目标大小来评价该个体性能优劣。在多目标优化算法中，往往采用Pareto层级排序来评价种群中不同个体的适应度。当个体的层级相同时，利用拥挤度来评价同层个体的适应度。层级越低，拥挤度越小，个体则越优，被选择概率也会越大。

2.1Pareto层级构造

考虑到Pareto层级构造过程在处理大规模问题时的高计算复杂度,本文提出了一种非回溯的Pareto层级构造方法，实时删除Pareto层级构造过程中产生的较差个体，大大加快了算法运行效率。其构造基本思想如下。

将父代种群纳入构造集中，从中选出一个比较个体(一般为种群中第一个个体)。用比较个体与归档集中其他个体进行一一比较,若比较个体支配其他个体或与其他个体的目标值相同，则将后者剔除。一轮比较过后，如果比较个体不被任何其他个体所支配，则比较个体即为非支配个体，将其纳入非支配解集，否则比较个体在该轮比较结束时也被剔除。按照这种方法进行下一轮比较，直至构造集为空。

在经过上述程序后，该构造集的非支配解集构造完成，其层数用1表示。随后，删除上一轮的所有非支配个体，形成新的构造集。同理，在新的构造集中，进行下一层的非支配解集构造,执行上述搜索过程，直至完成所有个体的层级构造。具体构造过程如下：

定义Q为构造集,Pop为比较集,q、q′是构造集中任意个体,Q1为被q支配的个体集合,Q2是Q中支配q的个体集合,Q3为与q无关且目标值不全相等的个体集合,Fi为第i层非支配解集。

(1)∀q∈Q,令i=1,Pop=Q-q。

(2)令Q1=∅,Q2=∅,Q3=∅,比较q和Pop中的每个个体q′的支配关系。若q支配q′,则令Q1←Q1+{q′}；若q′支配q,则令Q2←Q2+{q′};否则,若q、q′目标值不同，则Q3←Q3+{q′}。

(3)若Q2=∅，则Fi←Fi+{q}。

(4)Pop=Q2∪Q3,如果Pop中个体小于2个,则Fi←Fi+{Pop},转步骤(5);否则,转步骤(2)。

(5)Q←Q-Fi,Pop=Q,i←i+1。若Q=∅,则停止。否则,转步骤(2)。

2.2适应网格划分

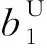
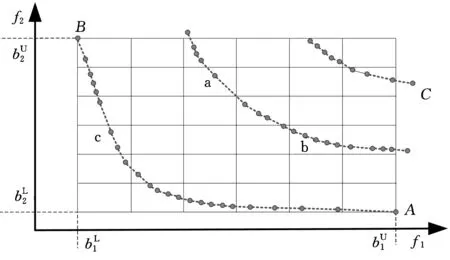
图1　双目标网格及边界

若个体q落在网格外，如图1中C点,则它肯定不是非支配解，将其拥挤度赋值为

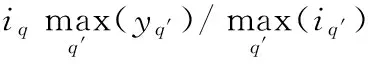
(11)

式中,iq表示个体q的层级;yq′为个体q′的拥挤度,q,q′∈{1,2,…,n};n为个体总数;cr为保留因子，考虑到网格外个体的多样性,取cr=0.8,则图1中C点的拥挤度为4。

网格划分的精度选择是算法设计时需考虑的问题。网格划分次数越多，群体分布精度越高，但必然耗费更多的计算时间。而过多的划分次数会使得所有个体的拥挤度为1，导致个体拥挤度的评价失效。借鉴文献[11]中的网格数确定思想，取网格划分次数为

(12)

其中,M为目标个数,n为种群中个体数目。式(12)表示网格划分次数取值为种群大小开目标个数次方并进行向上取整。

必须注意的是，在进化过程中，Pareto前沿在不断变化，网格边界也因此适应性地调整。新生个体的拥挤度需利用调整后的网格来确定。

2.3调整策略

考虑到所提出算法是基于归档集进行运算和输出的，故父代种群经过上述层级、拥挤度评价后，若所得非支配解数量超过归档集大小时，为保证算法运行效率，需对非支配解集进行筛选,并更新归档集。由于拥挤度评价针对的是所有个体，且非支配解层级为1，故引入了基于几何距离的调整策略。其具体步骤如下：

(1)求出非支配解集中任意两个个体间的相对距离：

(13)

其中,q,q′,q″∈{1,2,…,nnon},且q≠q′,nnon为非支配解数量,fqm为个体q的m维目标值。

(2)找出整个非支配解集中相对距离最小的两个个体q、q′。根据q、q′与非支配解集中余下个体的相对距离删除相关的个体,如由下式找出相对距离最小值，删除与该最小值相关的个体q或q′：

(14)

(3)将被删除个体与其他个体的的相对距离赋值为无穷大。

(4)如果剩下的个体数量满足条件则停止，否则转步骤(2)。

如果新产生的非支配解落在上一代确定的边界以外，则为了保持种群多样性，将这些个体直接放入归档集中。

3　混合多目标网格遗传算法

针对多目标汽车投产排序问题，本文提出一种新的混合多目标网格遗传算法(hybridmulti-objectivegridgeneticalgorithm,HmoGA)。该算法结合上文所提的多目标自适应网格选择方法，利用遗传算法的自然选择机理和群体进化机制完成寻优。

3.1编码与解码

考虑到编码的简洁与实用，采用字母方式进行编码。将最小生产循环单元内即将投产的全部产品排成一排，构成一个染色体。基因位的位置对应投产顺序,基因位的内容表示所投产的车型，染色体长度等于最小生产循环内要投产的产品数量。假设有3种车型(A,B,C)，投产比例为2∶1∶2,则其一个投产顺序可表示为(BCAAC)。

每隔一个生产节拍TC，就按此投产顺序投放一个产品上线。每一个生产循环单元的开始时间与节拍时间一致。例如,节拍为2min,每个生产循环单元内有5辆车,则第3个生产循环单元的开始时间为第21min。

根据上述投产顺序，利用式(4)～式(10)即可算出零部件消耗均衡度、车型调整费用、工位作业位置精准度三个目标值。

3.2归档集和进化种群选择

当非支配解数量超过归档集大小时,利用上述调整策略，选取满足归档集规定大小的个体。若未超过归档集规定大小，则直接将非支配解纳入归档集中。若非支配解存在极值点，则考虑极值点在单目标评价方面的优越性，将其直接纳入归档集中。归档集的更新从趋势上反映出Pareto前沿的推进过程，非支配解的选择保证了所存储非支配解的分布性。

同理，当非支配解集超过进化种群规定大小时，利用调整策略选取分布性较优的、满足进化种群规模的个体，构造出进化群体。当得到的非支配解集小于等于进化种群数量时，优先选择层级较小的个体,层级相同时选择拥挤度较小的个体。

3.3交叉个体选择

针对进化群体，采用轮盘赌方法选出即将执行交叉操作的个体，同时将个体的Pareto层级和拥挤度信息加入到轮盘赌选择概率的计算中, 分别算出目标层级和进化个体的选择概率和累计选择概率，再基于概率选择所需个体，目的是保证后代的收敛性、分布性。计算如下：

(15)

(16)

(17)

Zq=∑ziq

(18)

式中,pi为层级i的选择概率;Pi为层级i的累计选择概率;ziq为第i层个体集合中第q个个体的选择概率;Zq为第i层个体集合中第q个个体的累计选择概率;Ne为进化种群数量;Nei表示层级为i的个体数量;yiq为第i层个体集合中第q个个体的拥挤度。

式(15)、式(16)保证了层级越低，被选择概率越大;式(17)、式(18)保证在同一层级上，拥挤度越低，越可能被选择。

基于Pareto层级和拥挤度的概率计算，建立起一种精英评判和选择机制,使得父代中具有较好性能的基因片段能被继承下来，同时还有细微的扰动能力。

3.4邻域搜索

调整邻域结构在一定程度上可扩大搜索空间,拓展局部搜索能力。Chutima等[12]提出一种2-opt邻域搜索机制,在计算复杂度不高时有着良好的局部搜索性能。Ruiz等[13]采用转移变异算子将某个随机基因位上的基因插入到某两个相邻随机基因位之间来扩大搜索空间，并将该算子与相邻基因交换变异算子、任意两个基因交换变异算子进行比较，得出转移变异算子在邻域搜索性能和保持父代优秀基因等方面性能更优的结论。本文结合二基因位邻域搜索机制和转移变异算子，针对投产排序问题，设计出图2所示的2-opt邻域转移搜索算子。

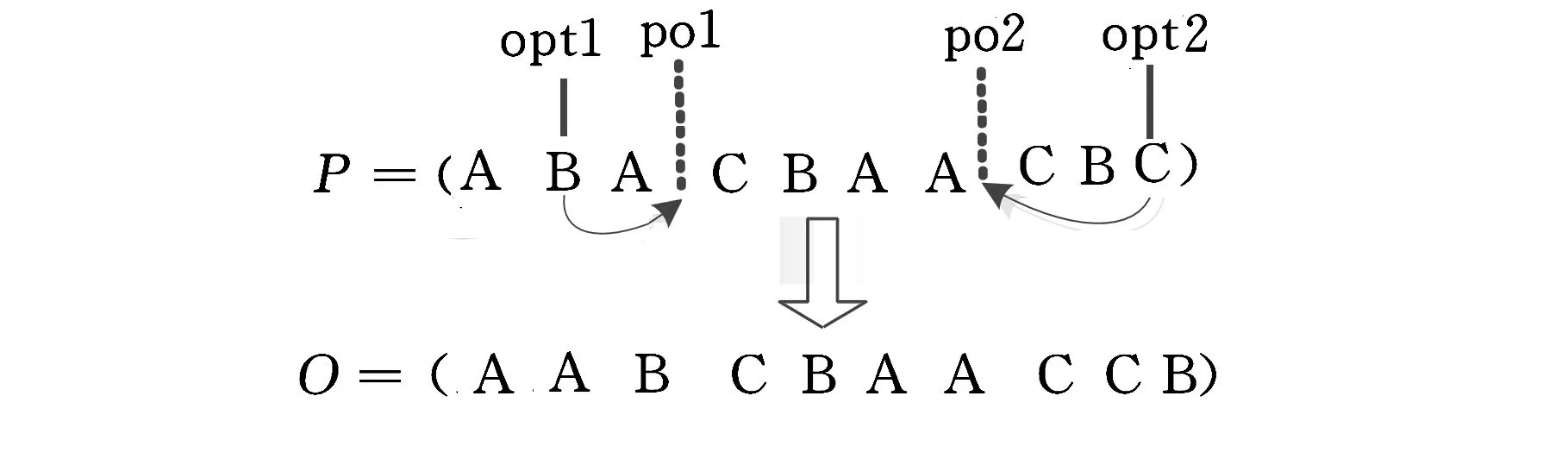
图2　2-opt邻域转移搜索

如图2所示，在父代个体P中已有的基因位置上任意选择两个基因(opt1，opt2)作为转移基因，再任意选择两个空位(po1, po2)作为转移目的地。将选出的基因转移到相应的目的地中。其他基因位顺次调整，生成后代个体O。

将该邻域搜索机制混入已提出的遗传算法中，改进了非支配解的邻域结构，以保证种群的多样性，提高集中搜索能力，加快收敛速度。

3.5算法流程

具体流程如图3所示。可以看出，基于相邻个体几何距离的调整策略、Pareto层级划分和拥挤度计算，在归档集构造、进化种群选择和交叉个体选择中起到了核心作用。同时，从进化种群中选择出来的个体，进行直接后继关系交叉(ISRX)[11]后生成子代Cchild1。对进化种群和子代Cchild1进行连续反演变异(INV)[11],生成子代Cchild2。对归档集进行邻域搜索生成子代Cchild3。将上述生成的所有子代群体和非支配解集的并集赋予父代种群。若达到了进化代数，则停止，否则对新一代父代群体进行Pareto层级划分、拥挤度评价，进一步完成归档集和进化种群的更新。重复上述操作，直到满足终止条件。

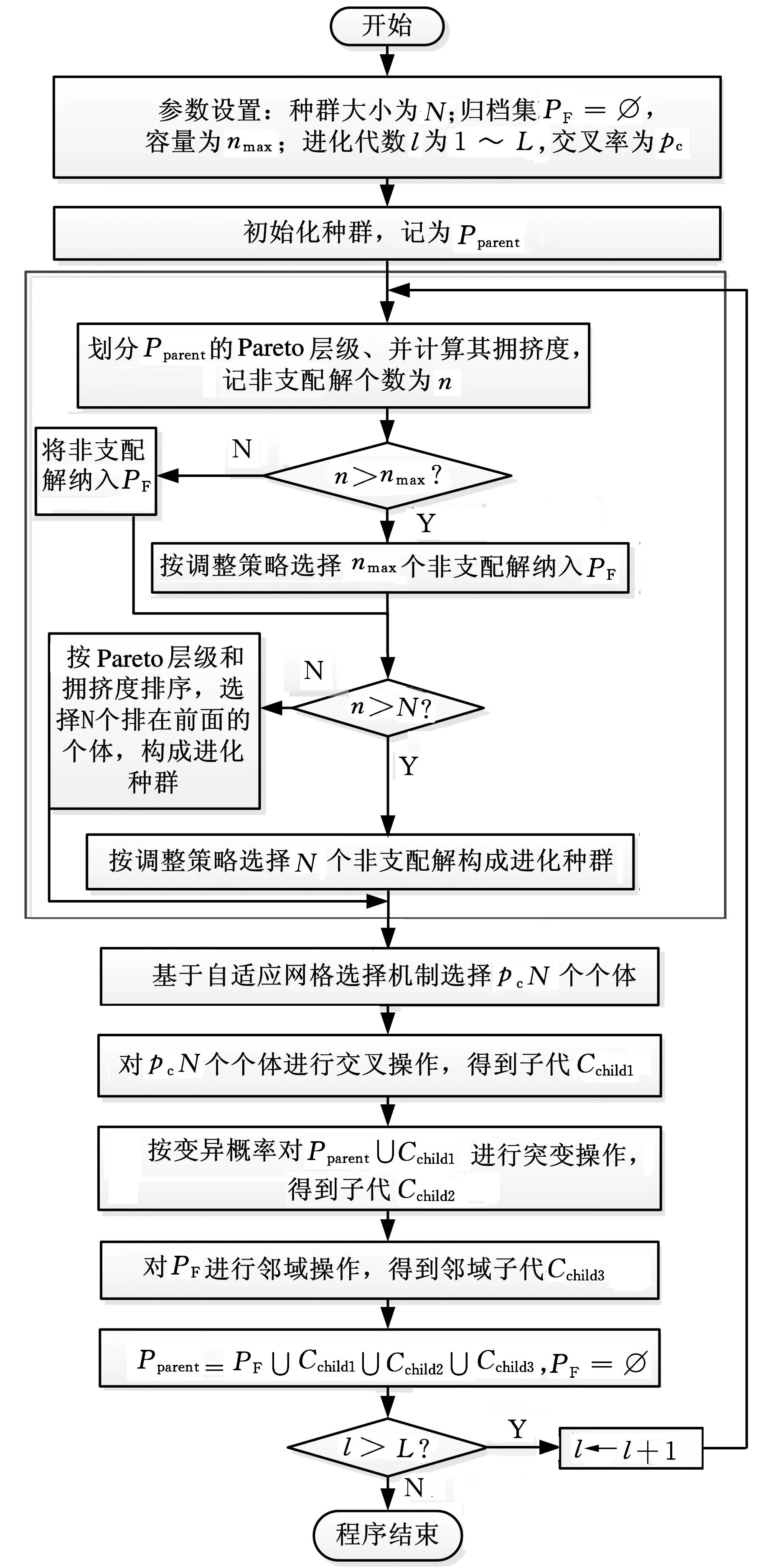
图3　HmoGA流程图

4　实验分析

为检验所提出的HmoGA的性能，利用MATLAB对上述算法和NSGA-Ⅱ[2]分别进行编码，并将运行结果与NSGA-Ⅱ进行比较。

4.1参数设定

某汽车厂生产线上有16个工位，需生产3种车型，排产比例为12∶10∶7,详见表1的p5问题。以p5为原型,进一步设计了表1所示的3个小规模(p1～p3)、1个中等规模(p4)和2个大规模(p6,p7)问题。其中,各种规模问题的复杂度即可行解数用下式进行计算:

nc=(∑dk)!/∏(dk!)

(19)

根据现场情况,将各车型对每种零件的消耗量取[0,10]的随机整数，各车型在每个工位上的操作时间取[60,120]s的随机数，各车型的调整费用取[0,10]元的随机数。考虑到计算时间的限制，将归档集的大小设置为500。种群大小、进化代数等其他参数设置如表1所示。

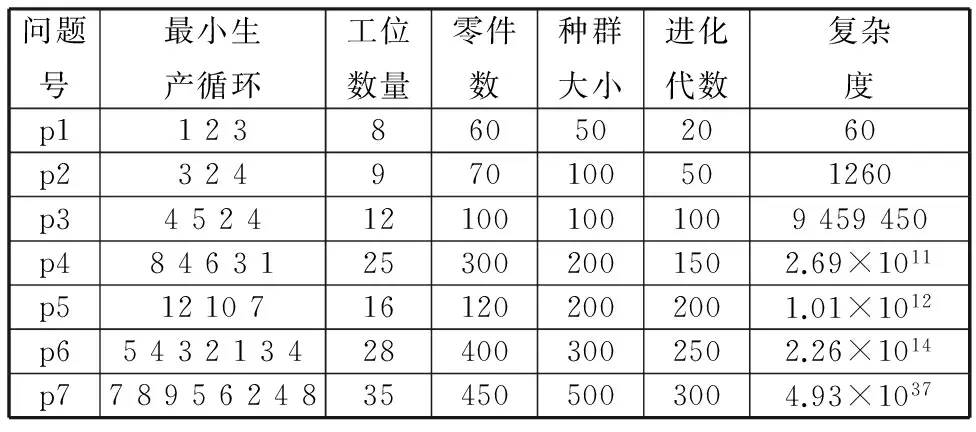
表1　投产测试集问题

由于生产节拍设置须满足生产需求，故先找出最小生产循环内总工作时间最长的工位，求取其每辆车的平均操作时间作为生产节拍。假定p1问题中各工位操作时间如表2所示，求得其生产节拍为112 s。

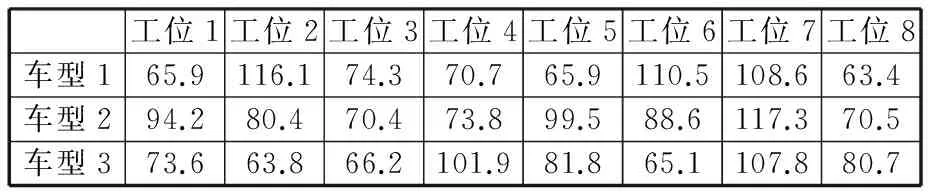
表2　p1问题的各工位操作时间　s

4.2排序方案性能分析

为检验使用HmoGA算法所求投产方案的正确性，以p1问题为例，求解得到了若干非支配解，见表3。同时，也利用枚举法求出p1问题的真实前沿解。

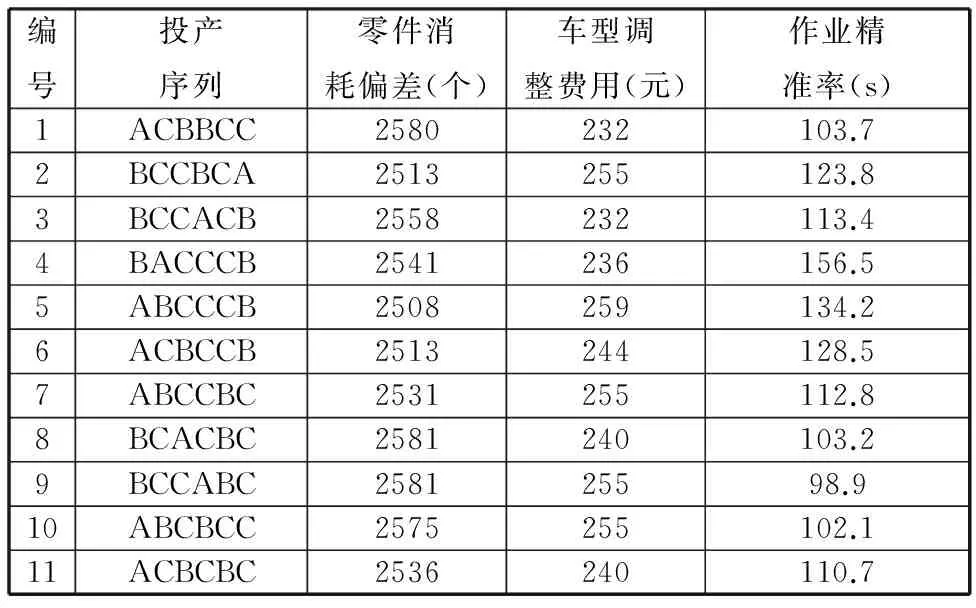
表3　p1问题非支配解及其目标值

两者对照表明,HmoGA得到了p1问题所有的真实前沿解，证明在小规模问题上该算法具有最优性。同时，在所有解中，零件消耗偏差、车型调整费用相差不大，而作业精准率的变化比较大。对于大规模问题，由于不可能用枚举法一一列出所有可行解来对其进行层级评价以求出其真实前沿解，因此HmoGA所求得的非支配解的属性无法通过与真实前沿比较来检验。后面将会通过和其他算法(NSGA-Ⅱ)对比来验证其非支配解性能。

在具体决策时，可根据各目标在生产实际中的重要性，以及所得非支配解中各目标值的变化率大小，确定各目标权重，选择最终投产方案。按照上述思想确定出p1问题的最优投产序列为(BCCABC)。由图4可见，若按此序列组织生产,则各工位装配总时间较均匀，不仅零件消耗偏差和车型调整费用较小，还能较好保证各工位的作业精准率。

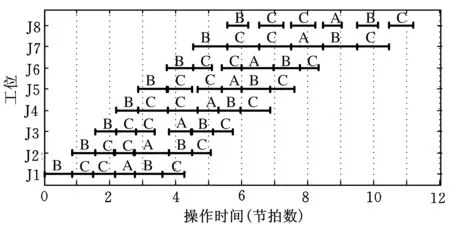
图4　多车型混流生产作业甘特图

4.3算法性能分析

NSGA-Ⅱ算法是当前综合性能最好、应用最广泛的多目标算法[1]，其求解效率高，收敛性能优，分布性能好，故选择该算法作为比较对象来评价HmoGA算法的性能。具体评价指标包括非支配率[10]、非支配解个数、相邻个体距离偏差[14]、相对百分偏差[13],计算结果见表4。在此基础上完成算法收敛性和多样性分析。

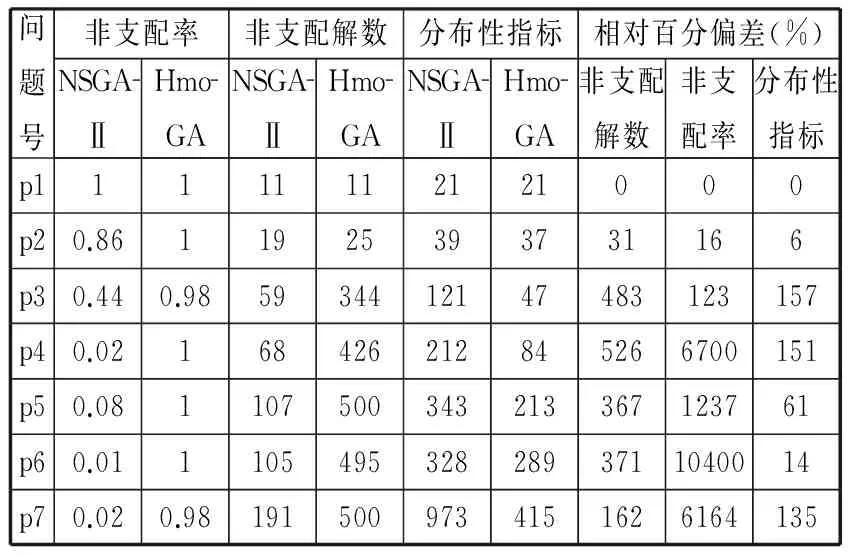
表4　两种算法所得投产排序方案性能比较

4.3.1收敛性分析

图5为p5问题利用HmoGA计算得到的非支配解收敛性优化图。可以发现，在进化过程中非支配解不断增加。第一代非支配解数量偏少，各目标值偏大。随着优化过程的进行，非支配解数量越来越多，收敛速度也越来越快，非支配解也越来越接近真实前沿。到100代时，收敛速度明显放缓，但还是在持续进行,到200代时还找到了一个新的分支。新算法极大改进了非支配解。

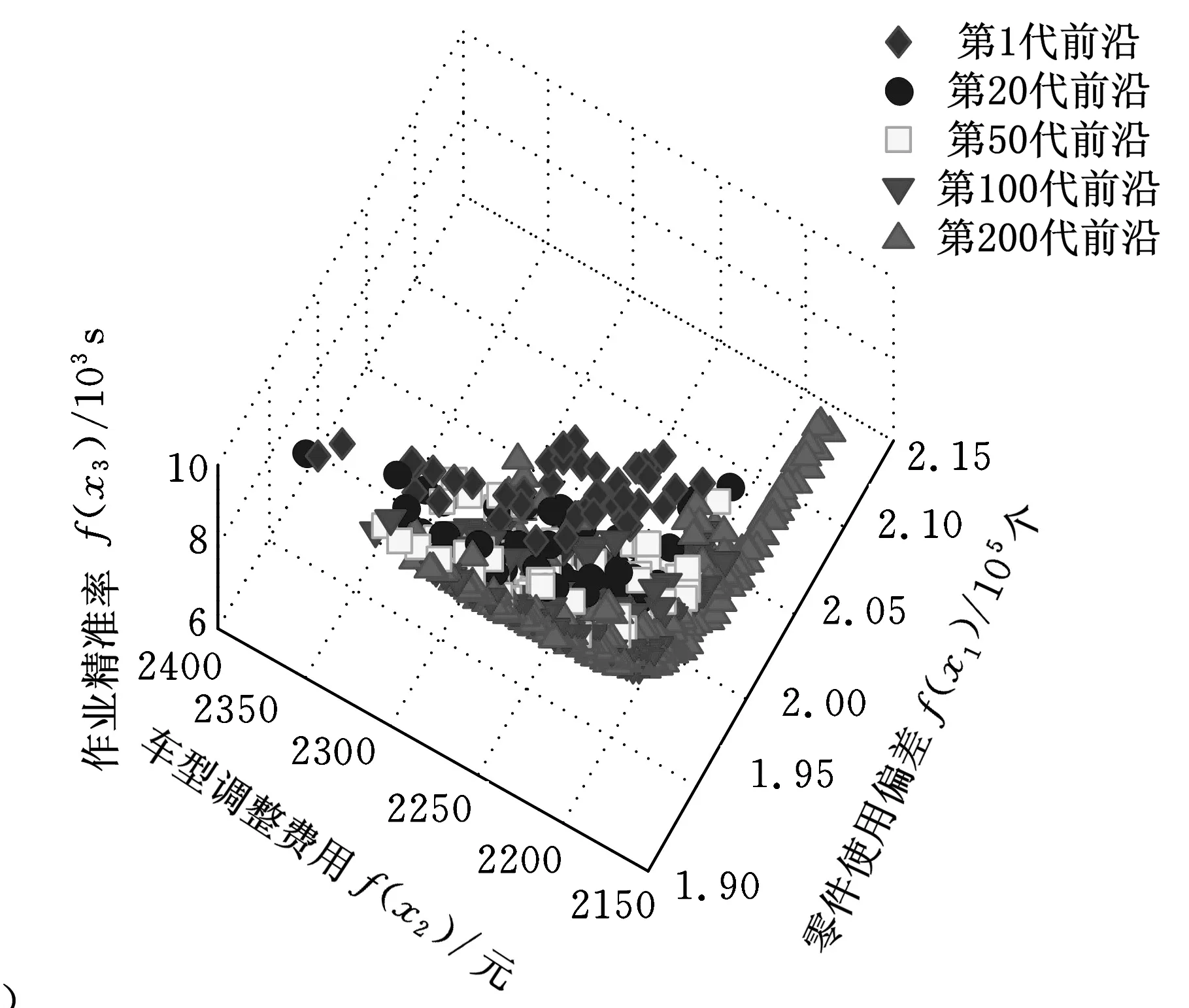
图5　HmoGA收敛性分析图

比较HmoGA和NSGA-Ⅱ两种算法的收敛性指标可知：在小规模问题中两种算法几乎找到了所有的非支配解；从中等规模问题开始，HmoGA所求非支配解基本上不被支配,而NSGA-Ⅱ的非支配解中至少有一半被支配。例如，HmoGA非支配率达到98%以上，其相对百分偏差最大值高达10 400%。

上述结果表明，HmoGA对中大规模问题具有更强的适应性，其非支配解更接近真实前沿。分析可知，通过层级评价机制，可使非支配解在进化前期迅速靠近真实前沿。同时，由于极值点保留机制和邻域搜索的存在，始终具有搜索到更多邻域结构的可能性。

4.3.2多样性分析

进化种群的多样性一般从两个方面进行分析：在一定空间内的个体数量、种群个体分布的均匀程度。图6示出了另一组随机参数下p4问题的非支配解数量和分布性指标随迭代次数增加的变动趋势。可以看出，在进化初期非支配解数量很少，分布性较差。随着不断进化，非支配解逐渐增多，相邻个体距离偏差持续减小，种群分布更均匀。当进化代数达到120代时，非支配解数量接近归档集大小，分布性指标基本不变。当非支配解数量超过归档集规定大小时(135代)，运用调整策略对非支配解进行筛选，保持了非支配解的分布性。

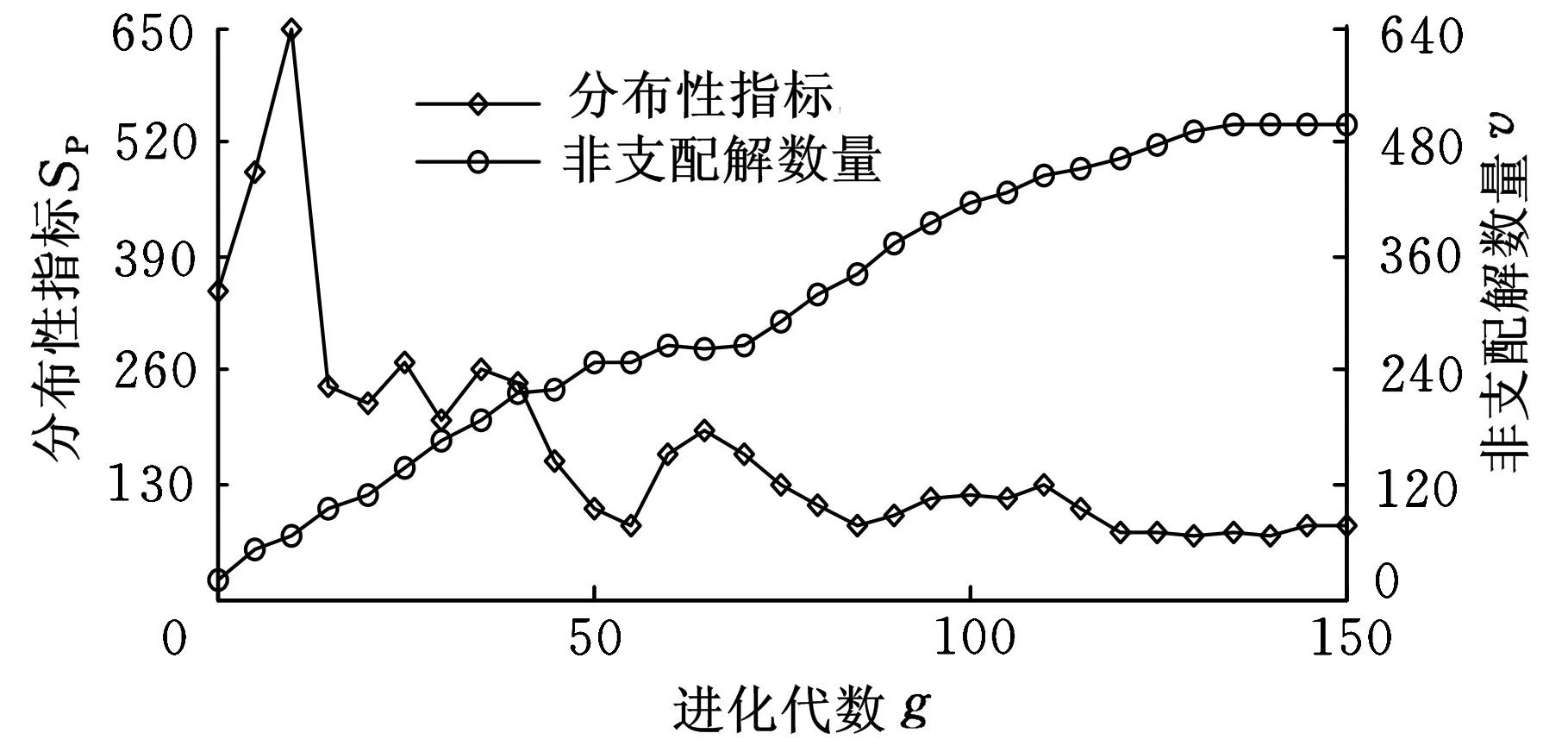
图6　多样性分析图

下面通过分析表4中的数据，进一步讨论非支配解的多样性。关于非支配解的分布性，在小规模案例中，两种算法基本能找出所有非支配解，分布性能基本相同。随着问题规模的增大,HmoGA的优势越来越明显。如表4所示，对于p3、p4、p7问题，HmoGA所得非支配解的分布性指标相对于NSGA-Ⅱ所得非支配解的分布性指标提高约150%。关于非支配解的数量，对于任一问题，HmoGA搜寻到的非支配解数远多于NSGA-Ⅱ。在小规模案例中两种算法都得到了相同的非支配解。随问题规模的增大，HmoGA所得到的非支配解数大大增加。以p4问题(图7)为例，其非支配解数小于归档集规模，HmoGA获得了426个非支配解，而NSGA-Ⅱ只获得68个。

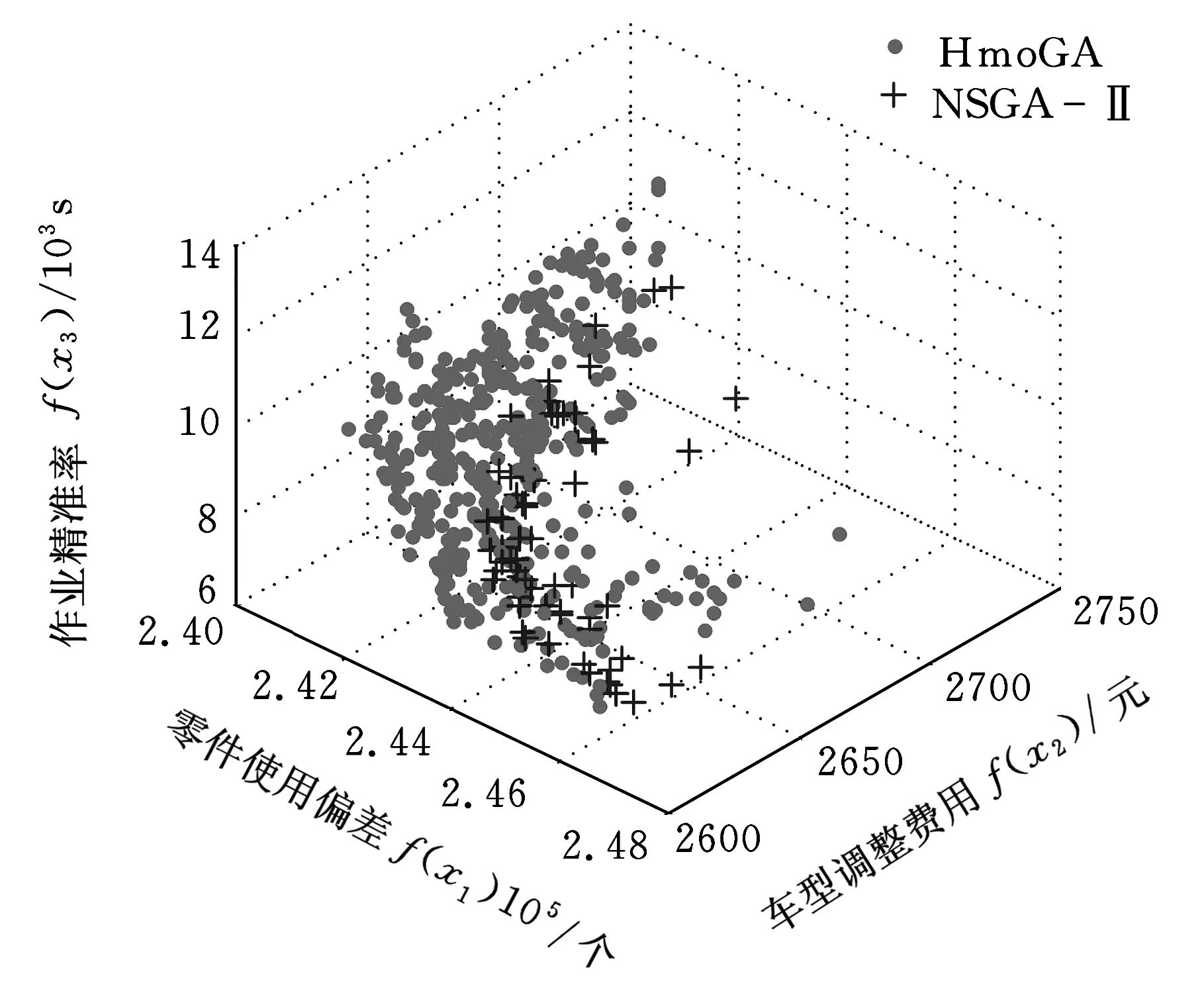
图7　HmoGA与NSGA-Ⅱ前沿比较

在问题规模很大时，如图8所示的P7问题，HmoGA所得非支配解数在110代时超过了归档集大小，若不采用调整策略,则搜索到的非支配解逐渐增多，相应的运行时间也会递增。采用分布性调整策略后，通过对非支配解集内部进行筛选，使非支配解数量保持在一定的范围内，同时算法的运行效率得到大幅提升。

综上所述，当算法陷入局部最优时，HmoGA的邻域搜索机制和突变操作可帮助算法寻找新的进化区域，能够适时地扩大搜索空间，跳出局部最优。 另外，相同个体排斥机制、拥挤度评价策略的存在能够及时删除目标值相同的个体，并以更大的概率选择分布性较好的个体，从而提高种群分布性。

5　总结

(1)针对某汽车公司的投产排序问题，提出了一种混合多目标网格遗传算法HmoGA,以便同时实现零件消耗偏差小、车型调整费用低和工位作业精准三个目标。针对上述实际问题和投产目标，设计了大、中、小三种规模投产案例，运用非支配率、非支配解数量和相邻个体距离偏差三个指标，对所提算法与经典多目标算法 NSGA-Ⅱ进行了性能比较,证明HmoGA算法在收敛性、解的数量和分布性方面都具有明显优势，特别是中大规模问题中其优越性更显著。

(2)将相同个体排斥机制加入到层级评价过程中，可使非支配解的分布更加均匀。

(3)融合基于相邻个体距离的种群调整策略，可增加算法的运行效率，促进均衡分布。

(4)利用2-opt迁移算子对非支配解进行邻域搜索，拓展了优秀基因的邻域结构。

综合性能较高的多个非支配解的存在，为企业后期决策提供更多的选择，对平衡生产线负载、提高员工积极性、缩短供货周期、增强核心竞争力，具有很大的作用。

[1]唐秋华,席忠民,陈平和,等.高效精准混装作业调度策略研究[J].中国机械工程,2007,18(9):1108-1111.

Tang Qiuhua,Xi Zhongmin,Chen Pinghe,et al.Research on Scheduling Strategy for High Efficiency & Punctuality in Mixed Model Assembly Line[J].China Mechanical Engineering,2007,18(9):1108-1111.

[2]Deb K,Pratap A,Agarwal S,et al.A Fast and Elitist Multi-objective Genetic Algorithm:NSGA-Ⅱ[J].IEEE Transactions on Evolutionary Computation,2002,6(2):182-197.

[3]刘敏, 曾文华, 赵建峰. 一种快速的双目标非支配排序算法[J].模式识别和人工智能,2011,24(4):538-547.

Liu Min,Zeng Wenhua,Zhao Jianfeng.A Fast Bi-objective Non-dominated Sorting Algorithm [J].Pattern Recognition and Artificial Intelligence,2011,24(4):538-547.

[4]鲍培明,朱庆保.用于多目标进化的归一化排序非支配集构造方法[J].电子学报,2009,37(9):23-28.

Bao Peiming,Zhu Qingbao.A Technique of Building Non-dominated Set Based on Normalized Sort in Evolutionary Multi-objective Optimization[J].Acta Mechanica Sinica,2009,37(9):23-28.

[5]杨虎,许峰.基于聚集密度的粒子群多目标优化算法[J].计算机工程与应用,2013,49(17):190-194.

Yang Hu,Xu Feng.Multi-objective Particle Sarm Optimization Algorithm Based on Crowding-density.Computer Engineering and Applications,2013,49(17):190-194.

[6]李志强,蔺想红.基于聚类的NSGA-Ⅱ算法[J].计算机工程,2013,39(12):186-190.

Li Zhiqiang,Lin Xianghong.Non-dominated Sorting Genetic Algorithm II Based on Clustering[J].Computer Engineering,2013,39(12):186-190.

[7]戚玉涛,刘芳,常伟远,等.求解多目标问题的Memetic免疫优化算法[J].软件学报,2013,24(7):1529-1544.

Qi Yutao,Liu Fang,Chang Weiyuan,et al.Memetic Immune Algorithm for Multi-objective Optimization[J].Journal of Software,2013,24(7):1529-1544.

[8]贾宁,马寿峰.基于启发式搜索和反馈修正的单路口控制方法[J]. 系统工程理论与实践, 2013, 33(2):444-449.

Jia Ning,Ma Shoufeng.A Traffic Signal Control Method for an Isolate Intersection Based on Heuristic Search and Feedback Correction[J].Systems Engineering Theory and Practice,2013,33(2):444-449.

[9]Tang Qiuhua,Li Jie,Floudas C A,et al.Optimization Framework for Process Scheduling of Operation-dependent Automobile Assembly Lines[J].Optimization Letters,2012,6(4):797-824.

[10]郑金华. 多目标进化算法及其应用[M].北京：科学出版社，2007.

[11]Hyun Chulju,Kim Yeongho,Kim Yeokeun.A Genetic Algorithm for Multiple Objective Sequencing Problems in Mixed Model Assembly Lines[J].Computers & Operations Research,1998,25(7/8):67.

[12]Chutima P,Naruemitwong W.A Pareto Biogeography-based Optimisation for Multi-objective Two-sided Assembly Line Sequencing Problems with a Learning Effect[J].Computers & Industrial Engineering,2014,69:89-104.

[13]Ruiz R,Maroto C,Alcaraz J.Two New Robust Genetic Algorithms for the Flowshop Scheduling Problem[J].Omega,2006,34(5):461-476.

[14]Coello Coello C A,Pulido G T,Lechuga M S.Handling Multiple Objectives with Particle Swarm Optimization[J].IEEE Trans. on Evolutionary Computation,2004,8(3):256-27.

(编辑苏卫国)

A Hybrid Multi-objective Grid Genetic Algorithm for Automobile Production Sequencing Problems

Tang Qiuhua1Hu Jin1Zhang Liping1Cao Xiaojun2

1.Wuhan University of Science & Technology,Wuhan,430081 2.Dongfeng-Peugot-Citroen Automation Co., Ltd.,Wuhan,430056

Three objectives were expected to be achieved simultaneously when sequencing automobiles in process,including equaling the spare parts consumption,minimizing the total adjustment cost resulting from exchanging automobile models,calibrating the work position for each automobile on any station.A new hybrid multi-objective grid genetic algorithm(HmoGA) was proposed based on Pareto stratum.In the algorithm,a new rejection mechanism was first considered in the sorting process of Pareto stratum,for the purpose of getting the even distribution of the non-dominated solutions.Then an adaptive grid selection scheme was designed by integrating Pareto stratum evaluation,crowding degree calculation and distance estimation among adjacent individuals.Thus,higher quality population can be generated,better parent chromosomes can be selected,and the distribution of the Pareto front can be improved constantly.Finally,the 2-opt shift operator was hybridized into the proposed genetic algorithm so as to broaden the search space and escape from local optimum.Three groups of experiments have done and three metrics including non-dominated ratio,the number of Pareto optimal solutions and the deviation of distances between neighbors were used as the performance measures.The results reveal that the proposed HmoGA dramatically outperforms NSGA-Ⅱ in terms of convergence and diversification.

Pareto stratum;crowding degree;adaptive grid selection;rejection mechanism;local search

2014-11-17

国家自然科学基金资助项目(51275366,51305311);高等学校博士学科点专项科研基金资助项目(20134219110002,2013M542073)；湖北省教育科学“十一五”规划课题(2007B215)

TH16;TP39DOI：10.3969/j.issn.1004-132X.2015.16.008

唐秋华,女,1970年生。武汉科技大学机械自动化学院教授、博士研究生导师。主要研究方向为生产过程与调度。胡进,男,1990年生。武汉科技大学机械自动化学院硕士研究生。张利平,女,1983年生。武汉科技大学机械自动化学院讲师。操小军,男,1970年生。神龙汽车公司技术中心首席工程师。