全矢LMD能量熵在齿轮故障特征提取中的应用

王洪明　郝旺身　韩　捷　董辛旻　郝　伟　欧阳贺龙

郑州大学,郑州,450001

全矢LMD能量熵在齿轮故障特征提取中的应用

王洪明郝旺身韩捷董辛旻郝伟欧阳贺龙

郑州大学,郑州,450001

齿轮故障信号具有非线性、非平稳特征,齿轮发生故障时,信号的能量结构随之改变,在不同的频带内能量不同。传统方法采用局部均值分解(LMD)提取振动信号的能量熵,将能量熵指标作为故障评判标准进行故障分类,依靠单一传感器信息源进行故障诊断，因而容易造成误诊、漏诊。全矢LMD能量熵法融合了双通道同源信息的回转能量，可降低故障误判率。通过实验模拟齿轮正常、齿根裂纹、断齿、缺齿等4种状态，验证了全矢LMD能量熵作为故障特征能达到很好的故障分类效果。

齿轮；非线性；LMD；能量熵；全矢；故障特征

0　引言

机械故障中齿轮故障较为常见,由齿轮故障带来的后果也是显而易见的。齿轮发生故障时伴随着由于结构改变而带来的撞击、摩擦，加之本身的非线性因素,反映出的振动信号往往是非平稳、非线性的。基于传统线性理论的信号分析方法处理非线性问题容易丢失设备的重要信息。能量熵法是一种基于复杂性测度的非线性信号处理方法，复杂性测度是反映非线性信号无序度的一个重要特征[1]。齿轮发生故障时其振动信号的能量结构将随之改变，不同的故障其能量在各个频带处也不同，据此可以通过监测振动信号的能量的变化情况来反映齿轮的运行状态。

局部均值分解(local mean decomposition,LMD)是Smith[2]提出的一种能将具有多分量的原始复杂信号分解成一系列PF分量的方法,LMD具有很好的自适应性,可改善经验模态分解(EMD)的端点效应。

传统的故障诊断技术是基于单通道信号的,容易造成误判。采用全矢谱技术融合LMD分解后的双通道信号的各个PF分量，进一步获取双通道信号的全矢LMD能量熵，能够有效地区别齿轮的常见故障，降低故障误判率。实验结果表明，全矢LMD能量熵法是一种可靠的齿轮故障特征提取方法。

1　全矢回转能量理论

(1)

设ZRk为Zk的实部序列,ZI k为Zk的虚部序列，则

(2)

理论上有4种方法来研究不同谐波下转子的全矢能量:①基于融合强度的能量法;②基于回转轨迹的能量法;③基于融合面积的能量法;④基于回转轨迹周长的能量法[3]。

基于回转轨迹的能量法误差最小,较稳定,综合能力较好,可以作为全矢能量分析的基本方法。因此本文采用基于回转轨迹的能量法。平面同源信息融合的回转能量为基于主振矢融合强度能量与基于副振矢融合强度能量之和[4],且为两个单源振动信号的能量之和。各谐波的主振矢与副振矢的平方和等于X和Y方向振动信号的幅值平方和。

设Ek(f)为信号的能量谱，则

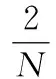
(3)

k=0,1,2,…,N/2-1

式中,f、T分别为信号的频率和周期。

将式(1)代入式(3)得

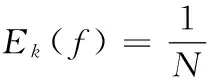
(4)

2　局部均值分解理论

设原始信号为x(t),其具体分解过程如下：

(1)将原始信号x(t)的局部极值点ni全部找出,求出两两相邻的局部极值点ni和ni+1的平均值mi,再用折线连接所有求得的平均值mi,构造初始均值函数[5],采用滑动平均法对初始均值函数进行平滑处理[6],得到一个局部平均值函数m11(t)。

(2)用找出的局部极值点ni,求得包络估计值ai:

(5)

用步骤(1)中的相同手段处理包络估计值ai得估计函数a11(t)。

(3)将局部平均值函数m11(t)从x(t)中分离出来,即

h11(t)=x(t)-m11(t)

(6)

(4)对函数h11(t)进行解调,即

(7)

(5)由步骤(3)和步骤(4)得

(8)

终止条件为[7]

(9)

(6)将上述在迭代运算过程中产生的各个包络估计函数a1q(t)相乘,得到的结果即为包络信号a1(t),也即瞬时幅值：

(10)

(7)将上述计算过程中求得的纯调频信号s1n(t)与包络信号a1(t)相乘,就得到信号x(t)的第一个PF分量:

PF1(t)=a1(t)s1n(t)

(11)

(8)将原始信号x(t)的第一个PF分量PF1(t)从其本身分离出来,剩余部分作为一个新的信号u1(t),再将u1(t)作为原始信号,重复步骤(1)～步骤(7),循环k次,直到最后所得信号uk单调时循环终止[7],即

(12)

原始信号x(t)经过LMD分解之后相当于k个被分离出来的PF分量和一个残余分量uk之和[7],即

(13)

构建LMD仿真信号：

x(t)=x1(t)+x2(t)

其中,x1(t)为调幅调频信号,x2(t)为调频信号：

x1(t)=(1+cos6πtcos(400πt+4cos8π)

x2(t)=3sin5πtsin100πt

采样频率1024 Hz,采样时长1 s,仿真信号及其LMD分解如图1所示。

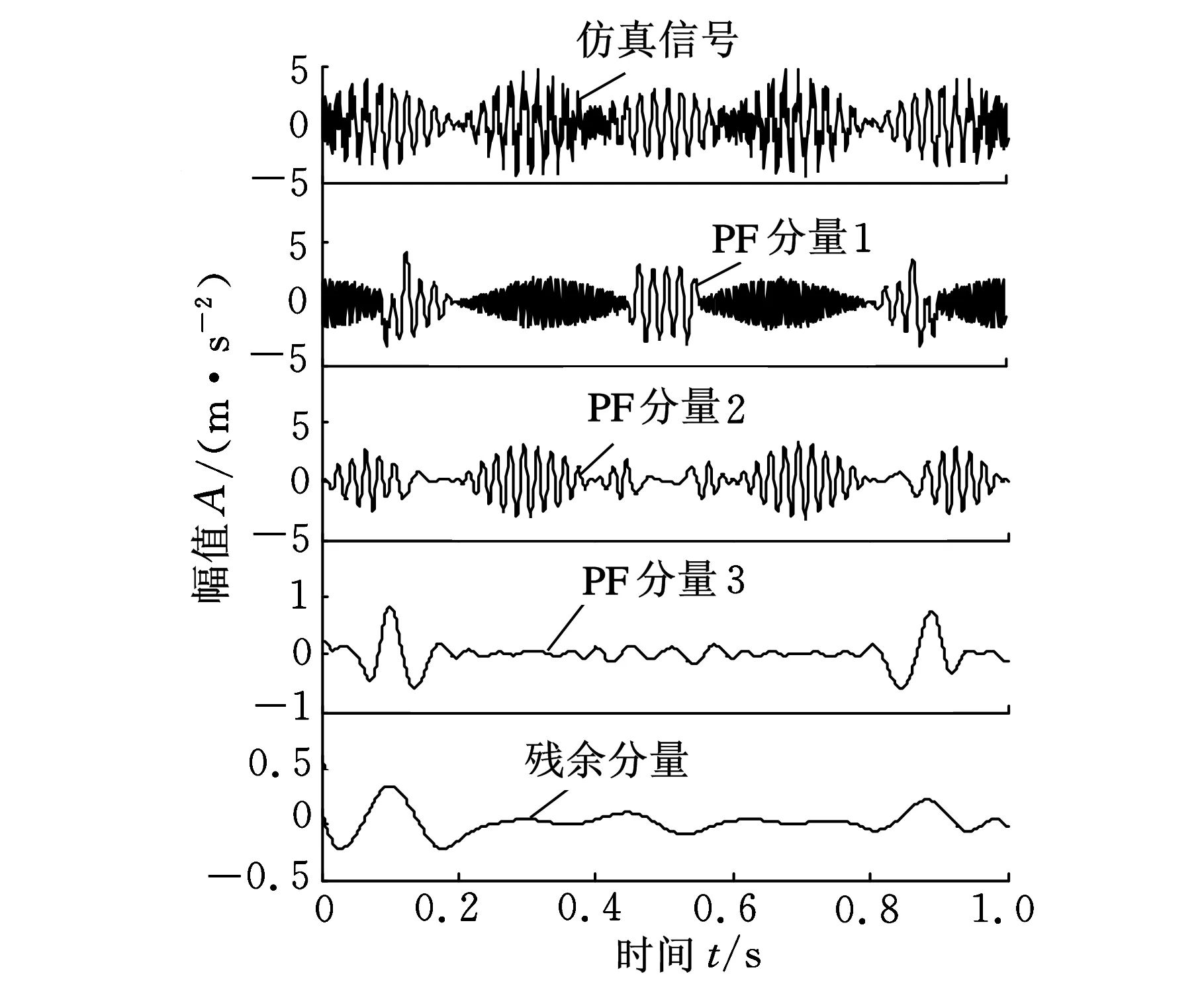
图1　仿真信号的LMD分解

3　全矢LMD能量熵

当齿轮出现不同故障时,其振动信号中频率的分布会突变,信号的能量结构也会随之发生改变。为了体现出能量结构在各个频率处的变化,可以对振动信号进行LMD分解得到一系列的PF分量,进而计算各个PF分量的能量。

对水平方向振动信号{xn}进行LMD分解,得到n个PF分量:PFx1,PFx2,…,PFxn,以及1个残余分量,各个PF分量处相应的能量为Ex1,Ex2,…,Exn；对垂直方向振动信号{yn}进行LMD分解,得到n个PF分量:PFy1,PFy2,…,PFy n,以及1个残余分量,各个分量处相应的能量为Ey1,Ey2,…,Ey n。设转子的全矢LMD能量为Eai(i=1,2,…,n)，则

(14)

易知LMD分解之后的残余分量极小,可以忽略不计,不影响信号的总能量，又因为LMD分解的正交性,故分解之后的n个PF分量的能量之和恒等于分解之前的原始信号的能量。根据Shannon信息熵[8]定义全矢LMD能量熵如下：

(15)

其中pa i=Eai/E表示双通道的第i个PF分量全矢融合后的能量占双通道振动信号总能量的百分比值,其中E=Ea1+Ea2+…+Ean表示双通道振动信号的总能量。由于在对数的运算过程中以e作为底,则延用Shannon信息熵的单位nat(nature unit)。图2是全矢LMD能量熵方法流程图。

图2　全矢LMD能量熵方法流程

4　全矢LMD能量熵实验

为了验证全矢LMD能量熵法对齿轮故障诊断的效果,进行了全矢LMD能量熵故障诊断模拟实验。实验采用美国Spectra Quest公司设计的可模拟风力涡轮机的动力传动故障诊断综合实验台(WTDS)，如图3所示，动力传动系统由1个二级行星齿轮箱、1个由滚动轴承支撑的二级平行轴齿轮箱、1个轴承负载和1个可编程的磁力制动器组成。本次实验将模拟输入轴直齿小齿轮的齿根裂纹故障、缺齿故障以及断齿故障，如图4所示。采用2组加速度传感器进行同步采集，传感器的具体布点可参照WTDS的说明书[9]。实验电机转速1800 r/min，采样频率7680 Hz,采样点数8192。3种故障X、Y双通道时域振动信号如图5所示。

图3　WTDS实验台

(a)齿根裂纹　(b)缺齿(c)断齿图4　输入轴小齿轮3种故障

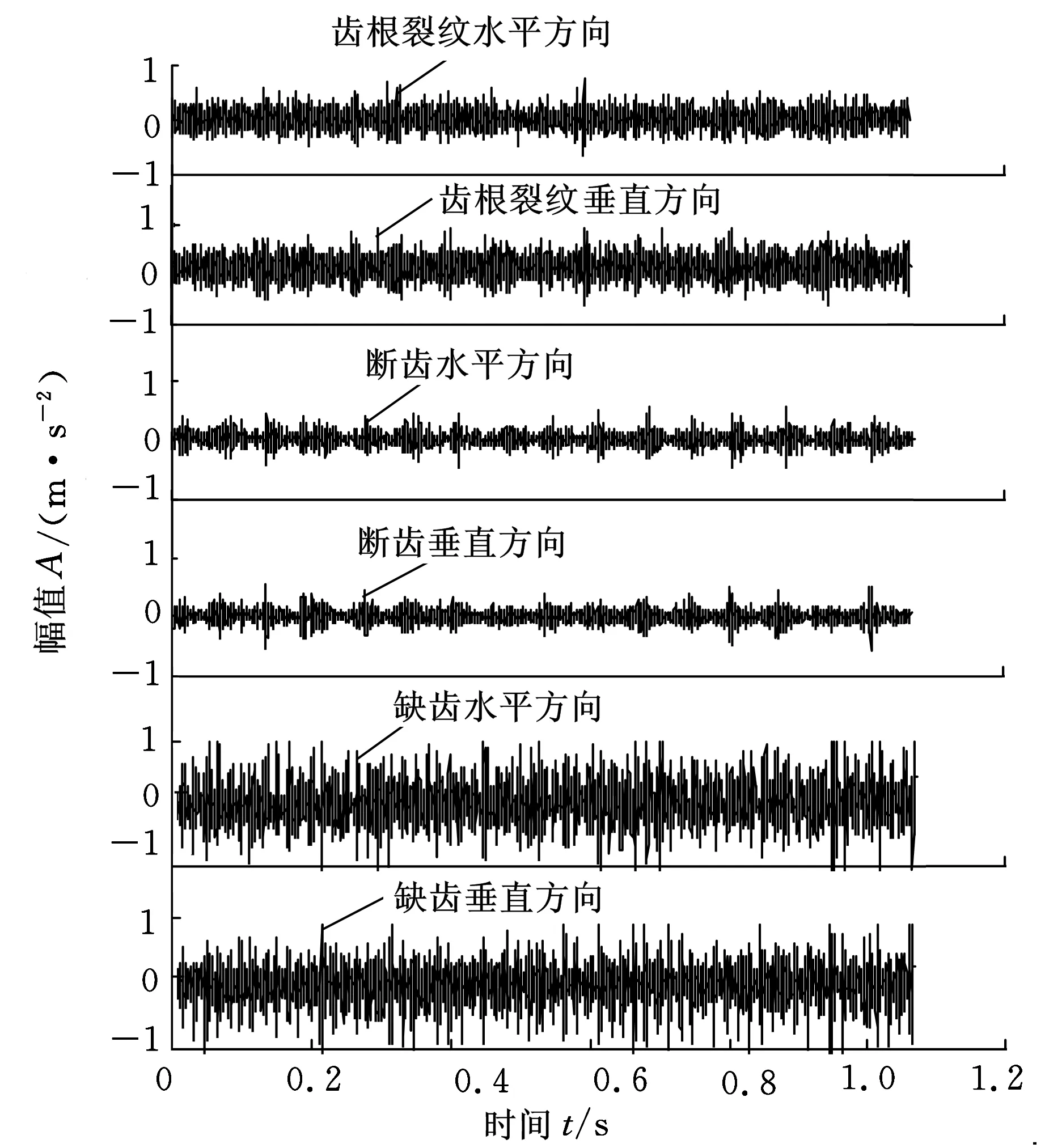
图5　3种故障双通道信号

通过对3种故障的X、Y同源双通道信号进行对比发现,即便针对同一种故障,2个方向的振动信号仍有较大区别。文献[10]指出，由于齿轮在工作过程中受力方向的不同,正好安装在受力方向的传感器采集到的信号往往更能真实地反映设备的状态。但是，在现场难以保证传感器的布点正好位于受力方向，采集的信息难以保证可靠性，对诊断结果的影响也是可想而知的。

分别对齿轮正常、齿根裂纹、断齿、缺齿4种状态的水平(X通道)和垂直(Y通道)方向各10组同源双通道信号进行LMD分解,均取前6个PF分量进行分析。

图6是缺齿状态的X通道信号的LMD分解图。表1所示为4种状态同源双通道信号的LMD能量熵以及经过全矢融合后的全矢LMD能量熵，篇幅所限，只展示前5组信号的LMD能量熵。由表1可知，同一种状态的X通道和Y通道的LMD能量熵均有差别，这种差别最终会影响对故障类别的判断。

图6　水平方向缺齿信号的LMD分解

nat

图7、图8所示分别是X通道和Y通道的LMD能量熵，比较两个通道的LMD能量熵发现，在X通道下，齿根裂纹的LMD能量熵高于正常状态下的LMD能量熵，但在Y通道下情况则完全相反，体现了两个通道信息的差异性，而理论上，正常状态的LMD能量熵应高于齿根裂纹故障状态的LMD能量熵。显然，若取X通道的信息进行分析易造成误判，因此有必要进行双通道信号的信息融合。

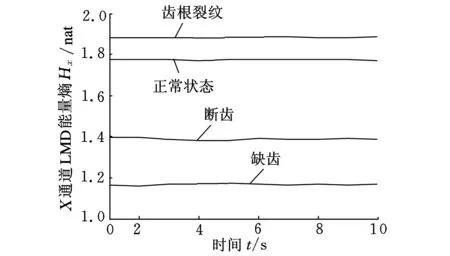
图7　4种状态X通道LMD能量熵

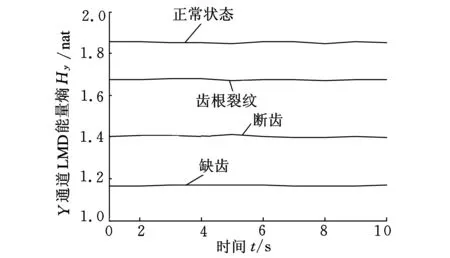
图8　4种状态Y通道LMD能量熵

图9　4种状态全矢LMD能量熵

图9所示是在选择前6个PF分量的情况下对每种状态10组信号共40组信号的全矢LMD能量熵的统计结果,从图中可以看出4种状态的全矢LMD能量熵区别明显。正常齿轮的全矢LMD能量熵值接近1.8 nat,明显大于另外3种情况,这是由于齿轮在正常状态下,其振动信号的能量在各个频段内的分布具有随机性和不确定性，复杂度最高，故其熵值最大。当出现齿根裂纹故障时，齿轮仍能相对平稳运行，此时的故障特征依然不明显，故其能量熵略有降低，约1.7 nat。当出现断齿故障后,振动信号在某一频带处会出现共振频率，信号整体会出现周期性的冲击，能量便会向共振频率处集中,能量的分布增加了确定性的因素,信号的自相似性升高，复杂度降低，故能量熵值减小。缺齿故障比断齿故障更为严重，能量集中最明显，故缺齿故障下的的全矢LMD能量熵最小。由上述分析可知，融合了双通道信息的全矢LMD能量熵实验结果与理论分析是一致的，在X通道信息失真的情况下依然能得出正确的结论。

上述实验在选择前6个PF分量进行全矢LMD能量熵分析的情况下能明显地区分4种状态。对相同的数据选择前9个PF分量分析时,正常状态和齿根裂纹的全矢LMD能量熵均在1.82 nat左右,断齿与缺齿的全矢LMD能量熵分别在1.45 nat和1.2 nat左右,此时正常状态与齿根裂纹裂纹故障难以区分开来,且整体上4种状态的全矢LMD能量熵较选择前6个PF分量时均略微有所增加(篇幅有限,不再展示),反映出第6个分量以后的PF分量中的噪声对能量熵产生的干扰。故在对信号进行LMD分解之后，应选择合适的分量进行分析，具体选择几个分量有待进一步探讨。

5　结论

(1)能量熵法在非线性信号处理方面具有一定优势，能够较好地表征信号的能量突变情况，结合齿轮的故障特征，可以定性地分析出齿轮故障类别。

(2)依靠单源信号的LMD能量熵来进行齿轮故障分析存在着遗漏信息造成误诊漏诊的风险，实验证明，将全矢技术与LMD能量熵法结合提出的全矢LMD能量熵法能够很好地降低这种风险。在工程实际中，通过合理选择传感器的类型和布点位置能够进一步保证诊断结论的可靠性。

(3)原始信号夹杂的噪声对能量熵有较大影响，噪声的随机性影响了最终的能量熵值，故笔者在选择PF分量时只选择前6个分量，实际上也是一个剔除噪声的过程。PF分量的选择准则有待进一步研究。

(4)为了进一步解决噪声干扰问题，下一步将考虑引进小波技术对原始信号进行降噪处理。本文实验模拟了齿轮的3种故障，通过对比3种故障的全矢LMD能量熵值的大小来定性属于哪一种故障，下一步将结合人工神经网络或支持向量机等人工智能算法实现故障自动分类。

[1]刘永斌.基于非线性信号分析的滚动轴承状态监测诊断研究[D].合肥：中国科学技术大学,2011.

[2]Smith J S.The Local Mean Decomposition and Its Application to EEG Perception Data[J].Journal of the Royal Society Interface,2005,2(5):444-450.[3]袁浩东,陈宏,侯亚丁.基于全矢小波包能量熵的滚动轴承智能诊断[J].机械设计与制造,2012(2):233-235.Yuan Haodong,Chen Hong,Hou Yading.Intelligent Diagnosis of Rolling Bearing Based on Full Vector Wavelet Packet Energy Entropy[J].Machinery Design & Manufacture,2012(2):233-235.

[4]韩捷,石来德.旋转机械的全信息能量谱分析方法研究[J].机械强度,2003,25(4):364-368.

Han Jie,Shi Laide.Study of Full Information Energy Spectrum Analysis Method of Rotary Machinery[J].Journal of Mechanical Strength,2003,25(4):364-368.

[5]程军圣,张亢,杨宇,等.局部均值分解与经验模式分解的对比研究[J].振动与冲击,2009,28(5):13-16.Cheng Junshen,Zhang Kang,Yang Yu,et al.Comparison between the Methods of Local Mean Decomposition and Empirical Mode Decomposition[J].Journal of Vibration and Shock,2009,28(5):13-16.

[6]李志农,刘卫兵,肖尧先,等.基于局域均值分解包络谱和SVM的滚动轴承故障诊断方法研究[J].机械设计与制造,2011(11):170-172.

Li Zhinong,Liu Weibing,Xiao Yaoxian,et al.Fault Diagnosis Method of Rolling Bearing Based on Local Mean Decomposition Envelope Spectrum and Support Vector Machine(SVM)[J].Machinery Design & Manufacture,2011(11):170-172.

[7]程军圣,史美丽,杨宇.基于LMD与神经网络的滚动轴承故障诊断方法[J].振动与冲击,2010,29(8):141-144.

Cheng Junshen,Shi Meili,Yang Yu.Roller Bearing Fault Diagnosis Method Based on LMD and Neural Network[J].Journal of Vibration and Shock,2010,29(8):141-144.

[8]Yang Yu, Yu Dejie, Cheng Junsheng.A Rolling Fault Diagnosis Method Based on EMD Energy Entropy and ANN[J].Journal of Sound and Vibration,2006,294(1):269-277.

[9]昊普特科技.风力涡轮机动力传动故障诊断仿真器(WTDS)[EB/OL].( 2013-04-17)[2014-11-11]http://www.haopute.com/p-998.html.

[10]韩捷,巩晓赟,陈宏.全矢谱技术在齿轮故障诊断中的应用[J].中国工程机械学报,2010,8(1):81-85.Han Jie,Gong Xiaoyun,Chen Hong.Applying Full Vector Spectrum for Gear Fault Diagnosis[J].Chinese Journal of Construction Machinery,2010,8(1):81-85.

(编辑华中平)

Full Vector LMD Energy Entropy in Gear Fault Feature Extraction

Wang HongmingHao WangshenHan JieDong XinminHao WeiOuyang Helong

Zhengzhou University,Zhengzhou,450001

Gear vibration signals in the events of failure were often non-stationary,non-linear.Energy structure would change in the fault signals,leading to different energy in different frequency bands.LMD was used to extract energy entropy of the vibration signals,and energy entropy was used as failure evaluation standards for fault classification.It is easy to be misdiagnosed with the traditional single channel signal diagnostic method.Full vector LMD energy entropy integrated two-channel homologous informations of vibration signals,and reduced the misdiagnosis rate.Through experiments the gear normal state,tooth root crack,broken teeth,missing teeth were simulated,and it is proved that with full vector LMD energy entropy as fault feature can achieve good fault classification results.

gear;non-linear;LMD(local mean decomposition);energy entropy;full vector;fault feature

2015-03-19

河南省教育厅自然科学研究项目(2011B460012)；河南省教育厅科学技术研究重点项目(13A460673)

TH133DOI：10.3969/j.issn.1004-132X.2015.16.006

王洪明,男，1989年生。郑州大学机械工程学院硕士研究生。主要研究方向为旋转机械故障诊断。郝旺身(通信作者),男,1976年生。郑州大学机械工程学院讲师、博士。韩捷，男，1957年生。郑州大学机械工程学院教授、博士。董辛旻，男，1968年生。郑州大学机械工程学院副教授、博士。郝伟，男，1963年生。郑州大学机械工程学院副教授、博士。欧阳贺龙，男，1989年生。郑州大学机械工程学院硕士研究生。