基于LMD能量信号和1.5维谱的轴承故障分析

张 昭，杜冬梅

（华北电力大学能源动力与机械工程学院，北京102206）

基于LMD能量信号和1.5维谱的轴承故障分析

张 昭，杜冬梅

（华北电力大学能源动力与机械工程学院，北京102206）

为了更准确的诊断滚动轴承是否发生故障，提出了利用Teager能量算子求LMD分量能量信号，再做其1.5维谱的方法。局部均值分解（Local Mean Decomposition，简称LMD）算法分解得到一组乘积函数分量，每一个分量都可近似看作一个线性平稳的单分量信号。Teager能量算子可以追踪信号瞬态能量，使故障冲击成分突出。1.5维谱具有降低频谱中高斯噪声影响的作用。新的故障诊断方法结合了各方法的优点，能有效地提取滚动轴承故障信号的特征频率及其倍频。通过对实测滚动轴承外圈、滚动体、内圈故障信号的分析，有效地提取了各种故障的特征频率，验证了新方法在滚动轴承故障特征提取中的可靠性。

滚动轴承；故障；分析；局部均值分解；Teager能量算子；1.5维谱

0 引言

滚动轴承具有摩擦阻力小、起动灵敏、效率高、润滑简便和易于互换等优点，广泛应用于旋转机械中，是机械系统的重要组成部件。滚动轴承的良好运行状态和运行寿命，关乎到整个机械系统的运行状态和寿命。滚动轴承的主要失效模式有疲劳破坏和永久变形两种［1］，一般都以凹坑的形式出现，当滚动体旋转经过该缺陷时便会对系统形成一个脉冲冲击。这些故障轻则使机械系统产生剧烈振动和噪声，重则影响系统的寿命，产生巨大的经济损失。

传统的轴承故障诊断方法需先对共振频率带进行滤波，然后再进行包络分析对轴承故障做出判断。但是需要人工选择滤波器的中心频率和带宽，对故障特征提取的准确性造成了一定的影响。近年来，有许多学者对轴承故障特征提取方法进行了研究，郑红等［2］采用谱峭度检测振动信号的瞬态频带，利用最优带通滤波器抑制振动噪声，由带通滤波器得到低频信号，并用双谱分析确定轴承故障的方法取得了良好的效果，但是，双谱具有分辨率低的特点。陈略等［3］提出噪声协助的经验模式分解（EMD）与1.5维谱相结合的方法进行抗混分解，提取故障的微弱特征信息，但EMD自身端点效应问题给特征频率的计算带来了一定误差。王天金等［4］提出基于Teager能量算子的频谱分析方法，具有良好的时间分辨率和自适应能力。但当信号信噪比较低时，频谱分析都容易淹没在噪声频率中，给轴承故障诊断带来困难。

为了准确得到轴承故障特征信息，本文提出基于局部均值分解（Local Mean Decomposition，简称LMD）能量信号和1.5维谱相结合的方法对轴承故障特征进行提取，通过对实测信号的轴承外圈、滚动体和内圈故障信号分析，验证了该方法的准确性和有效性。

1 LMD原理

LMD方法的本质是将原始信号分解为若干个瞬时频率具有物理意义的PF分量（Product Function，简称PF），每个PF分量由一个纯调频信号和一个包络信号相乘得到，获得纯调频信号和包络信号的过程［5，6］如下。

（1）确定原始信号x（t）所有的局部极值点ni，计算相邻两个极值点ni和ni+1的平均值mi，即

将所有相邻两个极值点的平均值mi用直线连接，然后采用移动平均方法进行平滑处理，得到局部均值函数m11（t）。

（2）采用局部极值点ni计算包络估计值

将所有相邻两个包络估计值ai用直线连接，然后采用移动平均方法进行平滑处理，得到包络估计函数a11（t）。

（3）将局部均值函数m11（t）从原始信号x（t）中分离出来，得到

（4）用h11（t）除以包络估计函数a11（t）以对h11（t）进行解调，得到

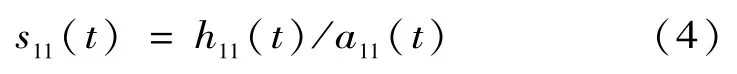
理想地，s11（t）是一个纯调频信号，即包络值为1。如果s11（t）不满足条件，则将其作为原始信号返回上述过程，直到某一调频函数s1n（t）的包络值为1时停止。应用中，纯调频信号的包络值不能准确的为1，可设置一个变动量Δ，当满足1-Δ≤a1n（t）≤1+Δ时，停止迭代。

（5）把迭代过程中产生的所有包络估计函数相乘便可以得到包络信号

（6）将包络信号a1（t）纯调频信号s1n（t）相乘便可以得到原始信号的第一个PF分量

（7）将第一个PF分量PF1（t）从原始信号x（t）中分离出来，得到一个新的信号u1（t），将u1（t）作为原始数据重复以上步骤，循环k次，直到uk为一个单调函数或常数为止。

最终原始信号可分解为若干个PF分量和一个残余分量uk，即

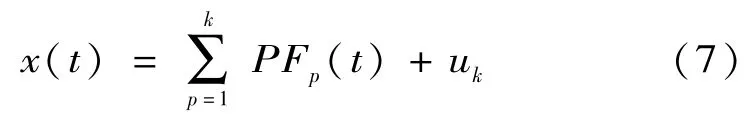
因为LMD方法在求取信号上下包络及均值时没有采用三次样条插值，其端点效应要大大的小于EMD方法，在故障信号分析中能够更准确的反映信号所携带的信息。

2 LMD能量信号

定义非线性信号算子ψ［7～9］

LMD能量信号可以计算振动信号某一频带内组分的瞬时总能量，使瞬态冲击成分更加突出，方便特征频率的提取，同时还有计算量小、响应迅速的特点。

3 信号的1.5维谱

零均值平稳随机过程x（t）的三阶累积量和三阶矩相等，三阶累积量定义［10，11］为

式中:E表示期望运算；τ1，τ2表示不同的时间延迟。取τ1=τ2=τ，得到三阶累积量的主对角切片

对c（t）进行一维傅里叶变换可得到x（t）的1.5维谱，即

1.5维谱为双谱在一维频率空间上的投影，由于零均值高斯噪声的三阶累积量值为零，因此1.5维谱相对于双谱不仅计算量减小，还保留了双谱对随机噪声的抑制作用和非二次相位耦合谐波的剔除能力。

对LMD能量信号求1.5维谱的方法同时结合了1.5维谱和Teager能量算子的优点，非常适用于冲击成分的检测中。其数学表达式为

式中:c3ψ（τ，τ）为PF（t）经过能量算子计算后的三阶累积量对角切片，文中对LMD能量信号的1.5维谱通称为1.5维能量谱。

4 实测信号分析

为了验证新方法的有效性，对美国凯斯西储大学轴承数据库公开的故障数据进行分析，本文选取电机驱动端SKF6205-RS深沟球轴承数据。轴承节圆直径39 mm，内圈直径25 mm，外圈直径52 mm，滚动体直径7.94 mm。轴承缺陷为电火花加工的直径为0.533 4 mm单点点蚀。信号采集时点蚀缺陷位于轴承外圈的最底部，采样频率12 kHz，分析点数6 000点，电机转轴频率（转频）29.95 Hz。轴承外圈、滚动体和内圈理论故障特征频率分别是107.36，141.17和162.19 Hz。

轴承产生点蚀缺陷，滚动体转经此处会产生一个冲击力从而使系统产生一个很高的共振频率。LMD算法是一种自适应的分解算法，分解结果为一组频率从高到低自动排列的近似平稳的单分量信号。为了更快的对轴承故障特征进行提取，只取分解得到前两个的高频分量进行分析即可，为方便说明问题，文中只列出了故障特征频率明显的LMD分量的1.5维能量谱。

4.1 轴承外圈故障分析

外圈故障信号如图1所示，经均值法滤波后，利用LMD算法分解得到4个PF分量。图2（a）为PF1分量的1.5维能量谱，从中可以清晰地看到轴承转轴频率30 Hz及其2倍频，外圈故障特征频率108Hz及其转频调制频率78 Hz和138 Hz，同时还可以看到其他一些二次相位耦合项的特征频率。图2（b）为PF2分量的1.5维能量谱，从中也可以清晰的看到轴承转频及其倍频和外圈故障频率。从图2整体看故障信号各频带谱线都非常清晰，频谱受噪声干扰非常小，图2（a）谱线基本不受所测信号中的噪声干扰。

图1 外圈故障信号

图2 PF1分量和PF2分量的1.5能量谱

图3为LMD求解PF1和PF2分量过程中产生的两条包络线直接做傅里叶变换求得的包络谱。对比图2和图3，可以看到图2谱线中带状噪声的影响远小于图3中噪声的影响，由此可见1.5维能量谱对噪声干扰的抑制作用。

4.2 轴承滚动体故障信号分析

滚动体故障信号如图4所示。经均值法滤波后，LMD算法得到3个PF分量，PF1的1.5维能量谱如图5所示。图中轴承转频及其倍频都很清晰，故障频率138 Hz也清晰可见，幅值却没有转轴频率及其倍频突出，说明滚动体故障能量十分微弱，容易淹没在其他周期成分或随机噪声中。图6为PF1分量的LMD包络线直接进行傅里叶变换得到的频谱，从中可以看到转轴频率30 Hz及其倍频很明显，虽然也可以找到138 Hz成分，但其峰值高度并不突出，基本淹没在其他峰值较小的频率信号中，不能确定是故障频率还是噪声频率。相比之下，PF1分量的1.5维能量谱在故障频率周围则没有其他频率成分，可以明确断定该频率即为滚动体故障特征频率，进一步验证了1.5维能量谱对噪声干扰的抑制作用。

图3 PF1和PF2分量的LMD包络谱

图4 滚动体故障信号

图5 PF1分量的1.5维能量谱

4.3 轴承内圈故障信号分析

内圈故障信号如图7所示，经均值滤波后做LMD分解得到3个分量。图8为内圈故障PF1分量对应的1.5维能量谱。图中29 Hz对应轴承转轴频率，59 Hz对应转轴的2倍频，轴承内圈故障特征频率162 Hz及其部分转频调制频率都非常突出，因此可以断定该故障为内圈故障。图9为利用LMD求解PF1过程中形成的包络线直接做傅里叶变换求得的频谱。图8和图9得到类似的结果。但是，图9频谱中噪声对分辨特征频率的影响明显较图8严重。

图6 PF1分量的LMD包络谱

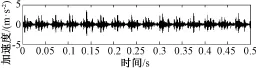
图7 内圈故障信号

图8 PF1分量的1.5维能量谱

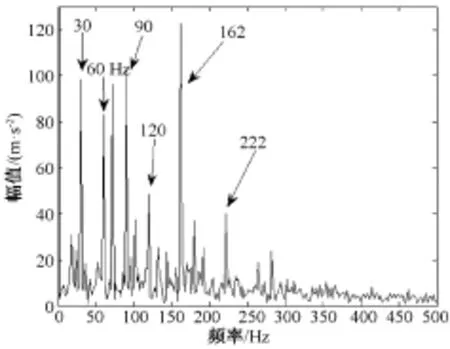
图9 PF1分量LMD包络谱

5 结论

（1）1.5维能量谱综合了Teager能量算子可追踪故障信号的瞬时能量，使冲击成分更突出的特点和1.5维谱降低频谱中高斯噪声影响的优点。并通过实测信号分析，验证了方法的有效性。

（2）LMD能量信号与1.5维谱结合可以有效地应用于滚动轴承故障信号的特征提取中，相对于传统滚动轴承故障特征提取减少了人工干预，增加了诊断的准确性。

［1］ 杨可桢，程光蕴，李仲生.机械设计基础（第五版）［M］.北京:高等教育出版社，2006.

［2］ 郑红，周雷，杨浩.基于谱峭度与双谱的轴承故障诊断方法［J］.北京航空航天大学学报，2014，40（9）:1176-1182.

［3］ 陈略，訾艳阳，何正嘉，等.噪声协助的EMD-1.5维谱信号抗混分解与特征提取［J］.振动与冲击，2010，29（5）:26-30.

［4］ 王天金，冯志鹏，郝如江，等.基于Teager能量算子的滚动轴承故障诊断研究［J］.振动与冲击，2012， 31（2）:1-5，85.

［5］ Smith J S.The local mean decomposition and its application to EEG perception data［J］.Journal of the Royal Society Interface，2005，2（5）:443-454.

［6］ 贾秀芳，安海清，张韶光，等.基于局部均值分解法的闪变包络线提取方法［J］.华北电力大学学报（自然科学版），2014，41（3）:10-16.

［7］ 程军圣，于德介，杨宇.基于EMD的能量算子解调方法及其在机械故障诊断中的应用［J］.机械工程学报，2004，40（8）:115-118.

［8］ 王晓龙.基于EEMD和Teager能量算子解调的故障诊断研究［J］.电力科学与工程，2013，29（3）: 18-22.

［9］ Zeng M，Yang Y，Zheng J D，et al.Normalized complex Teager energy operator demodulation method and its application to fault diagnosis in a rubbing rotor system［J］.Mechanical Systems and Signal Processing，2015，51-52:380-389.

［10］ 钟先友，曾良才，赵春华.局域均值分解和1.5维谱在机械故障诊断中的应用［J］.中国机械工程，2013，24（4）:452-457.

［11］ 段向阳，王永生，苏永生.切片双谱分析在离心泵故障诊断中的应用［J］.振动、测试与诊断，2010，30（5）:581-584.

Analysis of Roller Bearing Fault Based on Energy signals of Local Mean Decomposition and 1.5 Dimensional Spectrum

Zhang Zhao，Du Dongmei
（School of Energy，Power and Mechanical Engineering，North China Electric Power University，Beijing 102206，China）

In order to diagnose the fault of roller bearing more accurately，this paper proposes a new method，which uses Teager operator to calculate the energy of local mean decomposition（LMD）production functions and then figures out each 1.5 dimensional spectrum of them.LMD decomposes the fault signal into a group of product functions，each component can be considered as a linear stationary mono-component.Teager energy operator may calculate the transient energy of the fault signal，which can have a marked impact on roller bearing fault previously. 1.5 dimensional spectrum can reduce the effect of Gaussian noise in frequency spectrum.The new method combines the advantages of these algorithms，so it can extract fault characteristic frequency and its frequency doubling effectively.Through analyzing the test signals of outer raceway，ball and inner raceway fault，the paper achieved their fault characteristic frequency effectively and proved reliability of this method using in roller bearing fault feature extraction

rollerbearing；faults；analysis；localmeandecomposition；Teagerenergyoperator；1.5 dimensional spectrum

TH133.33；TH17

A DOI:10.3969/j.issn.1672-0792.2015.05.002

2015-03-30。

中央高校基本科研业务费专项资金资助项目（2014MS17）。

张昭（1990-），男，硕士研究生，研究方向为旋转机械状态监测与故障诊断，Email:z.zhang@ncepu.edu.cn。