基于改进多目标粒子群算法的冷连轧规程优化设计

魏立新　王利平　马明明　车海军　杨景明

燕山大学工业计算机控制工程河北省重点实验室，秦皇岛，066004

基于改进多目标粒子群算法的冷连轧规程优化设计

魏立新王利平马明明车海军杨景明

燕山大学工业计算机控制工程河北省重点实验室，秦皇岛，066004

合理的轧制规程能够提高轧机的产量和产品的质量，带来显著的经济效益。采用多目标粒子群算法，选择等相对负荷和预防打滑为目标进行冷连轧规程优化。针对算法存在的收敛性和分布性难以均衡的问题，引入一种基于平行坐标系的密度和收敛潜能计算方法；同时，为克服算法易于陷入局部最优的缺陷，提出一种带个体扰动的全局最优领导粒子选择策略。仿真结果表明，该方法能快速跳出局部极值，获得具有更好收敛性和分布性的近似Pareto前沿。最后应用该方法对某五机架冷连轧机进行了轧制规程优化。

多目标粒子群；冷轧规程优化；局部极值；收敛性；分布性

0　引言

长期以来，冷连轧轧制规程优化都是轧制控制领域的一项重要研究课题，其优化的实质内容是带钢的总厚度变形量在各机架之间的合理分配。随着轧制技术的不断发展，许多学者对规程优化进行了大量研究。传统的采用“计算-判断-修正”的单目标规程优化[1-2]虽然有明确的目标，但考虑的角度单一，使优化结果不尽合理。根据轧制规程的复杂性和优化目标的多样性，人们又提出了以加权系数聚合的多目标优化设计[3-4]，但由于目标函数量纲不统一，在多目标转化为单目标过程中权值难以确定，人为因素太多，结果也不能令人满意。

本文从提高板形质量、降低能耗、延长轧机使用寿命角度考虑，选择等相对负荷和预防打滑[5]为目标，建立了轧制规程多目标优化模型[6]。根据粒子群算法收敛迅速、计算量相对较小等优点[7]，将改进的多目标粒子群算法[8]应用到冷连轧规程优化中，并针对粒子群算法存在的收敛性和多样性难以均衡的缺陷[9]进行了改进；当算法陷入局部最优时，提出了一种带个体扰动的全局最优领导粒子选择策略，取得了很好的效果。

1　轧制规程优化模型

冷连轧规程优化的目的是使轧制过程处于最佳状态，实现节能轧制，并充分发挥轧机的生产能力，同时保证产品质量。本文选用等相对负荷和预防打滑进行优化。

1.1前滑模型

在冷连轧实际生产中，薄窄料容易产生打滑现象，会直接影响带钢表面的质量，严重时出现划痕，导致成品被判报废。根据白振华等[5]提出的打滑因子，设计了轧制规程优化预防打滑的目标函数。打滑因子为

(1)

式中，Δh为绝对压下量，mm；R′为工作辊压扁半径，mm；μ为摩擦因数；T、T0为前后张力，kN；F为轧制力，kN；γ为中性角；α为咬入角。

很显然，打滑因子ψ越大时，表示中性面离变形区的中部越远，越容易发生打滑现象；相反，打滑因子越小，发生打滑的概率越小。考虑到各机架轧制的整体性和彼此的差异性，预防打滑的目标函数可表示为

(2)

式中，β1和β2为相关权重系数；n为机架数；ψi为第i机架打滑因子。

1.2等相对负荷目标函数

在冷连轧机组中，为了更充分地发挥轧制设备的能力，可按各机架主电机的相对负荷来制定规程，其目标函数为

(3)

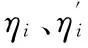
1.3规程优化约束条件

冷连轧机在实际生产中会受到设备因素和工艺因素的约束，其中工艺约束有

εmin≤ε≤εmax

(4)

Tmin≤T≤Tmax

(5)

式中，εmin、Tmin分别为允许的最小压下率、最小张力；εmax、Tmax分别为允许的最大压下率、最大张力。

设备因素约束有

Mi≤MiM

(6)

Fi≤Fimax

(7)

(8)

式中，Mi、Fi分别为第i机架电机实际力矩和实际轧制力；MiM、Fimax分别为第i机架电机额定轧制力矩和设备所能承受的最大轧制力。

1.4轧制规程多目标优化数学模型

本文以等相对负荷、预防打滑为目标，建立多目标优化数学模型：

(9)

式中，J为目标函数；X为变量；gi(X)为第i个约束条件。

2　改进的多目标粒子群算法

粒子群算法[10]可如下描述：设搜索空间为D维，个体总数为Psize；第i个粒子位置表示为Xi=(xi1,xi2,…,xiD)；第i个粒子在寻优过程中的历史最优位置为Pi=(pi1,pi2,…,pid)，设Pg为所有Pi(i=1,2,…,n)中的最优值；第i个粒子的位置变化率(速度)为向量Vi=(vi1,vi2,…,viD)；每个粒子的速度和位置按照如下公式进行更新：

vid(t+1)=ωvid(t)+c1rand()(Pid(t)-

xid(t))+c2rand()(Pgd(t)-xid(t))

(10)

xid(t+1)=xid(t)+vid(t+1)

(11)

i=1,2,…,N;d=1,2,…,D

式中，vid(t+1)为下一代粒子的速度；vid(t)为当前代粒子的速度；ω为惯性因子；c1、c2为正常数，称为加速因子；rand()为[0，1]之间的随机数；Pid(t)为个体的历史最优领导粒子；Pgd(t)为所有粒子的全局最优领导粒子；xid(t+1)为下一代粒子的位置；xid(t)为当前粒子的位置。

在多目标粒子群算法中，最优解集存在多样性和收敛性难以平衡[9]以及易于陷入局部最优的缺陷。本文采用基于平行坐标系(parallelcellcoordinatesystem,PCCS)的多目标粒子群优化算法(MOPSO)，通过计算外部集密度和收敛潜能来平衡收敛性和分布性，并加入带个体扰动的全局最优领导粒子选择策略，有效避免了算法陷入局部极值。

2.1收敛性能和分布性能的分析

首先通过下式将外部集中的粒子映射到一个N行M列的平行坐标系中：

(12)

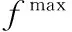
在分布性方面，根据下式计算平行坐标系中任意两个矢量之间的距离：

(13)

式中，S(Pi,Pj)为第i个和第j个粒子之间的距离，当Pi和Pj映射到同一个表格时，将两个向量之间的距离设置为0.5。

一个粒子的分布性受到周围所有粒子的影响，根据下式得到该粒子Pi的密度Den(Pi)：

(14)

密度越小，被选为领导粒子的可能性也就越大。而对于密度较大的粒子，当外部集的大小达到允许的最大值时，将被删除。

外部集中粒子的适应值越大，则离真实的Pareto前沿越远，收敛性能就越强。根据下式计算出外部集中粒子的收敛潜能Pot(Pi)：

(15)

在算法进化过程中，当粒子接近真实Pareto前沿时，粒子的收敛潜能会下降到一个稳定值，此时算法逐渐收敛。

2.2基于Pareto熵和个体扰动的全局最优领导粒子的选择

熵是一种检测微观分布均匀性的方法，通过Pareto熵来检测外部集中粒子的分布性，采用熵差来表示外部集中粒子相邻迭代时刻熵的变化大小，从而推测出种群发现新解的能力，估计种群的收敛状态和分布状态，进而确定领导粒子的选择方案。

熵H(t)和熵差ΔH(t)由如下公式定义：

(16)

ΔH(t)=H(t)-H(t-1)

(17)

式中，Knm(t)表示外部集中粒子映射到平行坐标系后，第n行m列的格子中的坐标分量个数。

将外部集中粒子的密度Den(Pi)和收敛潜能Pot(Pi)分别从小到大排序，选择按Den(Pi)排序的前n个作为最优密度集dgb，选择按Pot(Pi)排序的前n个作为最优潜能集cgb。在进化前期，算法产生较多的新解来支配旧解，从而推动种群向真实的Pareto前沿收敛，此时熵和熵差变化较大，随机选择cgb中的粒子作为全局最优领导粒子Pgd；在进化后期，种群逼近真实的Pareto前沿后，算法发现的新解只能支配当前解集中极少的个体，仅能引起Pareto熵和熵差的很小的变化，此时随机选择dgb中的粒子作为全局最优领导粒子Pgd。

粒子群算法的特点在于其学习机制和信息共享机制，粒子通过外部集中的全局最优领导粒子和自身经验来调整速度和位置，从而忽略了其他粒子的信息，使算法易于陷入早熟收敛。因此，当算法多代未更新且多代选用同一个全局最优值时，增加一个扰动向量，使算法跳出局部极值。从种群中随机选择与当前个体相互支配或支配当前个体的粒子作为扰动粒子。第i个粒子第d维的速度和位置按照下式进行更新：

vid(t+1)=ωvid(t)+c1rand()[Pid(t)-xid(t)]+

c2rand()[Pgd(t)-xid(t)]+c3rand()[Pdd(t)-xid(t)]

(18)

xid(t+1)=xid(t)+vid(t+1)

(19)

i=1,2,…,N;d=1,2,…,D

式中，Pdd为随机选出的扰动粒子的第d维。

判断新产生的扰动粒子与当前全局最优领导粒子的支配关系，若当前全局最优粒子被新粒子支配，则替换为新粒子。

经过多次仿真验证，加入个体扰动后的算法有效避免了陷入局部极值。采用测试函数ZDT2分别对基于PCCS的MOPSO算法[9]和加入个体扰动的MOPSO算法进行仿真验证，算法迭代200代，得到的结果如图1、图2所示。

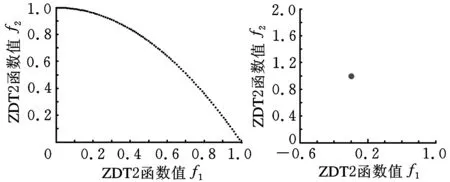
图1　加入个体扰动的MOPSO算法(t=200)图2　基于PCCS的MOPSO算法(t=200)

将算法分别运行30次，加入个体扰动的MOPSO算法，30次均收敛到近似Pareto前沿。而未引入个体扰动的基于PCCS的MOPSO算法仅有12次能收敛到近似Pareto前沿，多数情况会陷入局部极值，如图2所示。

2.3轧制规程优化流程

根据现场的生产条件以及工艺参数，为了保持带钢板形的良好，本文将末机架作为平整机使用，仅对前四机架进行优化，第5机架采用固定压下率方式，压下量约为5%～10%。优化设计的基本思想是，根据给定带钢的初始数据，随机初始化前4个机架的压下率分配比，利用MOPSO算法求出使目标函数最小的压下率分配方案。算法步骤如下：

(1)初始化种群参数。设定种群大小为150。外部集大小与种群大小一致。最大迭代次数为200。

(2)根据约束条件，产生初始种群和外部集。

(3)判断外部集的个数是否大于所允许的最大值，若大于，则根据拥挤距离策略，删除密集的多余个体，保证外部集个体数为最大值，执行(4)。否则，直接执行(4)。

(4)按照支配关系更新个体历史最优领导粒子Pid。

(5)根据式(12)～式(15)，计算外部集的每个粒子的密度和收敛潜能，获得外部集中粒子收敛性和多样性参数，并根据Pareto熵检测种群收敛和分布状态，更新全局最优领导粒子Pgd。

(6)判断算法是否陷入局部最优，若种群陷入局部极值，根据式(18)～式(19)，采用带个体扰动的全局最优领导粒子更新机制，跳出局部极值，执行(7)。否则，直接执行(7)。

(7)根据粒子的速度和位置更新公式(式(10)、式(11))，对粒子进行更新，产生新的种群。

(8)将产生的新种群放入外部集，并根据支配关系更新外部集。

(9)判断是否满足终止条件，是则执行下一步，否则转到(4)。

(10)输出外部集，获得近似最优Pareto前沿。

3　仿真验证

为验证轧制规程的优化效果，本文选用某钢厂1250mm冷连轧机为例，来料宽度为1000mm，来料厚度为1.5mm，要求成品厚度为0.3mm，此宽度下轧机的纵向刚度为3200kN。其他参数见表1。

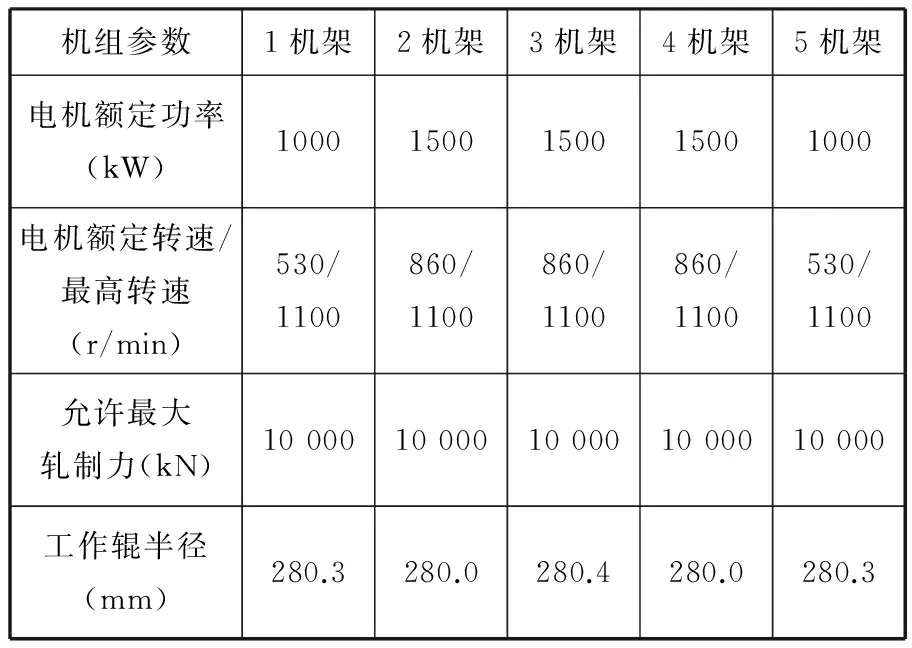
表1　1250 mm冷连轧机技术参数

根据本文选用的MOPSO算法，得到冷连轧规程优化的近似Pareto前沿与原规程对比如图3所示。图3中，点“·”为优化出的近似Pareto前沿，五角星“☆”为原规程。可以明显地看到，优化出的近似Pareto前沿在原规程下方，则必然存在优于原规程的解。但图中近似Pareto前沿反映的是两个目标的折中关系，若想降低打滑指标，则必然要损失功率指标，在实际轧制过程中，决策者可根据近似Pareto前沿，依据现场需要，选取适当的解。

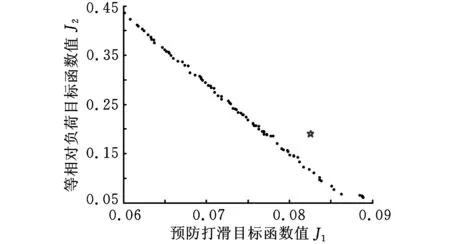
图3　最优Pareto前沿解集与原规程对比图

4　结语

本文针对冷连轧机预防打滑和等相对负荷目标函数，采用了多目标粒子群优化算法进行优化，并针对多目标粒子群算法存在的收敛性和多样性难以平衡的缺点，采用基于平行坐标系的方法，根据外部集中粒子的收敛程度和分布程度适当地选取全局最优领导粒子，当算法陷入局部最优时，采用带个体扰动的全局最优领导粒子选择策略,取得了明显的效果。

[1]魏立新，李兴强，李莹，等．基于改进自适应遗传算法的冷连轧轧制规程优化设计[J]．机械工程学报，2010，46(16)：136-141．

Wei Lixin，Li Xingqiang，Li Ying，et al．Optimization of Tandem Cold Rolling Schedule Based on Improved Adaptive Genetic Algorithm[J]．Journal of Mechanical Engineering，2010，46(16)：136-141．

[2]杨景明，窦富萍，刘舒慧，等．基于遗传算法的冷连轧轧制规程优化设计[J]．中国机械工程，2007，18(15)：1868-1871．

Yang Jingmin， Dou Fuping， Liu Shuhui，et al． Application of Genetic Algorithm to Rolling Schedule in Tandem Cold Mill[J]．China Mechanical Engineering，2007，18(15)：1868-1871．

[3]陈东宁，姜万录，王益群．基于粒子群算法的冷连轧机轧制负荷分配优化 [J]．中国机械工程，2007，18(11)：1303-1306．

Chen Ningdong，Jiang Wanlu，Wang Yiqun．Load Distribution Optimization of Tandem Cold Mill Based on PSO Algorithm[J]．China Mechanical Engineering，2007，18(11)：1303-1306．[4]杨景明，王春鹏，车海军，等．基于改进ABC算法的铝热连轧规程优化设计[J]．塑性工程学报，2013，20(5)： 91-96．Yang Jingming，Wang Chunpeng，Che Haijun，et al．Improved ABC Algorithm Based on Aluminum Hot Strip Mill Rolling Schedule Optimization Design[J]．Journal of Plasticity Engineering，2013，20(5)：91-96．[5]白振华，连家创，王骏飞．冷连轧机以预防打滑为目标的压下规程优化研究[J]．钢铁，2003，38(10)： 35-38．

Bai Zhenhua，Lian Jiachuang，Wang Junfei，et al．Screw-down Schedule Optimization for Preventing Slippage on Cold Tandem Mill[J]．Iron and Steel，2003，38(10)：35-38．

[6]李勇，刘建昌，王昱．改进权重自适应GA及冷连轧轧制规程多目标优化[J]．控制理论与应用，2009，26(6)： 687-693．

Li Yong，Liu Jianchang，Wang Yu．An Improved Adaptive Weight Approach GA for Optimizing Multi-objective Rolling Schedules in a Tandem Cold Rolling[J]．Control Theory & Applications，2009，26(6)：687-693．

[7]陈绍新．多目标优化的粒子群算法及其应用研究[D]．大连：大连理工大学，2007．

[8]Reyes Sierra M, Coello Coello C A．Improving PSO-based Multi-objective Optimization Using Crowding，Mutation and ε-Dominance[C]//Lecture Notes in Computer Science. Guanajuato, Mexico, 2005: 505-519.

[9]Hu Wang，Yen G G. Adaptive Multi-objective Particle Swarm Optimization Based on Parallel Cell Coordinate System[J]．IEEE Evolutionary Computation，2014，19(1)：1-18．

[10]Kennedy J，Eberhart R C.Particle Swarm Optimization[C]//Proceedings of the IEEE International Conference on Neural Networks. Perth, WA: IEEE, 1995: 1942-1948.

(编辑苏卫国)

Optimization of Tandem Cold Rolling Schedule Based on Improved Multi-objective Particle Swarm Optimization Algorithm

Wei LixinWang LipingMa MingmingChe HaijunYang Jingming

Key Lab of Industrial Computer Control Engineering of Hebei Province,Yanshan University,Qinhuangdao,Hebei,066004

Reasonable rolling schedule could improve the quality of the mill’s production and products thus bring significant economic benefits. The multi-objective particle swarm algorithm was adopted to optimize the objective functions of equal relative load and the slip rate. According to the problems that convergence and distribution were difficult to balance, based on parallel cell coordinate system a novel method was proposed to assess the evolutionary environment including density and potential of convergence. Meanwhile, to enhance the ability of escaping from local optima, a disturbance vector strategy was proposed for selecting global best. Simulation results show the improved strategy can be able to prevent falling into local extremum point, and improve the convergence and distribution of approximate Pareto front. The method was applied to a five-stand tandem cold mill rolling schedule optimization.

multi-objective particle swarm; cold rolling schedule optimization; local extremum; convergence; distribution

2014-10-21

国家自然科学基金委员会与宝钢集团有限公司联合资助项目(U1260203)；国家自然科学基金资助项目(61074099)；河北省高等学校创新团队领军人才培育计划资助项目(LJRC013)

TG335.13DOI：10.3969/j.issn.1004-132X.2015.09.020

魏立新，男，1977年生。燕山大学电气工程学院副教授。研究方向为冶金综合自动化与智能控制等。出版专著4部，发表论文50余篇。王利平，女，1989年生。燕山大学电气工程学院硕士研究生。马明明，男，1990年生。燕山大学电气工程学院硕士研究生。车海军，男，1974年生。燕山大学电气工程学院副教授。杨景明，男，1957年生。燕山大学电气工程学院教授、博士研究生导师。