一种针对圆形设计容差的二元测量系统能力评价的新方法

吴小芳　何　桢　施亮星

天津大学,天津,300072

一种针对圆形设计容差的二元测量系统能力评价的新方法

吴小芳何桢施亮星

天津大学,天津,300072

在一些测量过程中,测量仪器测得的数据是二维的,且设计容差为一个圆,当二元被测质量特性具有相关性时,无法直接利用常用的一元测量系统能力评价指数对圆形设计容差的二元测量系统进行分析和评价。提出了一种基于面积之比构造评价指数的方法,利用测量误差椭圆面积与设计容差圆面积之比和测量误差与测量值的椭圆面积之比建立测量系统能力评价指数,将常见的一元测量系统能力指数延伸到二元测量系统中,通过多元方差分析(MANOVA)估计评价指数来评价二元测量系统的能力。通过实例对该方法进行了验证。

测量系统能力；二维数据；重复性与再现性；多元方差分析

0　引言

测量系统分析是企业质量持续改进工作中的

重要内容，也是企业进行质量改进的第一步。制造商在分析过程能力和过程或产品质量控制之前，需要对测量系统能力进行分析。测量系统分析关注的主要问题是测量过程是否有能力准确并可靠地反映所测对象的波动，因此我们需要对测量系统能力进行分析和评价[1]。测量系统能力分析就是分析测量系统在各个变异源的影响下,测量系统对过程或产品控制而言能力是否充分。

国内外学者对一元测量系统分析已有深入研究。何桢等[2]采用基于三因素交叉嵌套混合效应模型的方差分析法对包含多台测量仪器的一元测量系统能力进行了分析。储晓承等[3]采用正态模糊化方法对在机测量系统的性能进行了模糊综合评价。Burdick等[4]对一元测量系统能力分析方法进行了综述。Li等[5]利用西格玛管理中的DMAIC方法,通过提高木材工业中的测量系统能力来改进质量。Woodall等[6]研究了常用的一元测量系统能力评价指数之间的关系。Erdmann等[7]研究了在医院中如何评价测量系统的能力。Nachtsheim等[8]提出了一种比较客户和供应商的测量系统能力的方法。Deldossi等[9]在测量系统能力的研究中，提出了一种对变异成分建立置信区间的方法。目前,关于二元以及多元的测量系统能力的研究相对较少。

被测质量特性x和y之间若存在相关性,则直接对变量x和y分别进行一元测量系统能力评价是不恰当的。忽略x和y之间的相关性多元方差分析不能准确地反映二元测量系统的能力。Majeske等[10]利用测量系统误差的多元正态分布特性，提出用多元方差分析(multivariate analysis of variance,MANOVA)方法估算多元测量系统能力评价指数。本文作者曾提出一种基于向量的多元测量系统能力分析方法[11]。Wang等[12]利用面向过程的基础的申述(POBREP)方法评价多元测量系统能力。Wang等[13]利用主成分分析(PCA)法对多元测量数据降维，然后分别计算各主成分对应的一元评价指数来评价多元测量系统能力。Peruchi等[14]利用加权主成分分析(WPCA)方法对多元测量数据降维,分别对主成分计算出一元评价指数，加权求得多元测量系统能力评价指数值，并与其他方法(MANOVA和PCA)进行了比较。

在一些测量过程中,被测质量特性是两个变量,若设计容差相互独立,则设计容差为矩形;若设计容差不独立,则设计容差为椭圆形或圆形。例如，离心泵转动装置的测量数据为二维测量值,设计容差为圆。Voelkel[15]对二元测量系统分析方法进行研究，提出了一种基于圆形直径(circle-diameter)的方法,利用MANOVA方法估计出测量所得的两维数据相关的变异成分并利用特征值建立圆周直径。Shannon[16]在Voelkel研究的基础上对动平衡的二元测量系统进行了分析研究。Wang等[17]针对设计容差为圆形的二元测量数据,利用bootstrap方法对相关方差的圆形直径建立置信区间。目前关于设计容差为圆形的二元测量系统能力分析的研究较少。针对设计容差为圆形的二元测量系统，本文在对一元测量系统能力评价指数进行深入分析之后，提出了一种基于面积的二元测量系统能力分析方法。

1　测量系统能力评价指数

常用的一元测量系统能力评价指数有三种,即精度公差比(precision-to-tolerance ratio,PTR)RPT、重复性与再现性百分比(%R&R)PR&R、信噪比(signal-to-noise,SNR)RSN等。RPT是测量系统的波动与被测质量特性容差之比;PR&R是质量特性真值与测量系统误差的标准差之比；RSN是测量系统误差与测量值的标准差之比[18]。这三种评价指数被广泛用于评价测量系统的能力,其定义分别为

(1)

式中,σG、σM与σQ分别为测量误差、测量值以及被测质量特性真值的标准差;σTOL为质量特性的设计容差。

由RSN与PR&R定义可知测量误差的准确度不依赖于规格限。

Montgomery等[19]指出,RPT<10%时表明测量系统能力足够。RSN取值大于5时,测量系统能力是不可接受的。AIAG[18](automotive industry action group)提出这样的准则:当RPT和PR&R中有一个大于30%时,说明测量系统能力不充分,需要改进测量系统;当RPT和PR&R都小于10%时,说明测量系统能力充分;而当RPT和PR&R中的最大值在10%～30%之间时,测量系统能力是否可接受取决于测量对象的重要度以及测量设备成本与维修费用等。因此本文仅考虑RPT和PR&R这两个评价指数。

对于二维测量数据,无法直接应用一元测量系统能力评价指数进行评价。多元统计方法如主成分分析(PCA)方法被广泛应用于质量工程实践中,用以解决多元能力问题。Hubele等[20]针对二元正态过程提出了一种利用矩形区域的三组分过程能力评价指数。Ch’ng等[21]提出了一种基于单变量指数加权平均的多元过程能力指数。然而这些多元统计方法很少被用在多元测量系统中。RPT、PR&R作为一元测量系统能力指数,也可以利用这些多元统计方法应用到多元测量系统能力评价中。

2　基于面积之比的二元测量系统能力评价

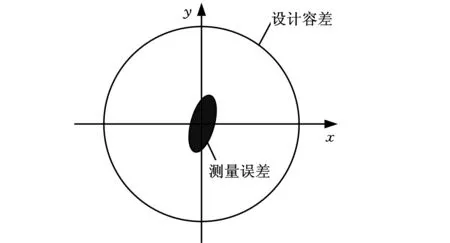
图1　测量误差、设计容差和测量值的(1-α)100%区域

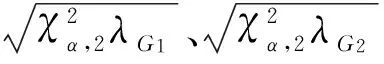
(2)

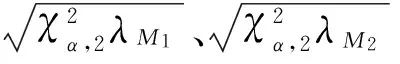
(3)

进行重复性与再现性试验，通过估计测量误差、被测质量特性真值以及测量值的方差-协方差矩阵,计算出相应的特征值,利用式(2)和式(3)就可以估算出二元测量系统能力评价指数RPT2和PR&R2,从而评价设计容差为圆的二元测量系统能力。

3　二元测量系统能力评价指数的估计

3.1重复性与再现性研究

总变异来源主要有部件、操作者、操作者与部件之间的交互作用以及重复测量效应等。本文考虑的二元测量系统的重复性与再现性研究数据采用两因素随机效应交叉模型。两因素为部件和操作者，其中操作者为随机因素。在重复性与再现性试验中，测量p个部件，操作者有o个，每个部件被同一操作者反复测量r次，测得的二维数据(xijk，yijk)用向量Mijk表示。则两因素随机效应交叉模型为

Mijk=μM+Pi+Oj+TPOij+εijk

(4)

i=1,2,…,p;j=1,2,…o;k=1,2,…,r

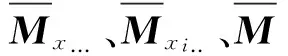
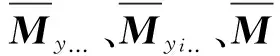
3.2评价指数估算步骤

(1)进行多元方差分析,需要考虑是否存在交叉效应TPOi j。

(2)估算出矩阵ΣG、ΣP和ΣM。

首先分别计算出部件效应、操作者效应、部件与操作者交叉效应以及误差项的均方矩阵EMSP、EMSO、EMSPO和MMSE。EMSP矩阵的元素EMSPxx、EMSPyy和EMSPxy分别为

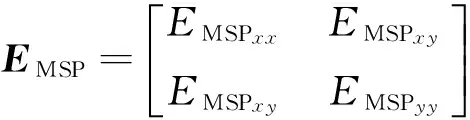
EMSPO矩阵的元素EMSPOxx、EMSPOyy和EMSPOxy分别为

误差项均方矩阵EMSE的元素EMSExx、EMSEyy和EMSExy分别为

根据相应的期望均方,分别计算出部件效应、操作者效应、部件-操作者交叉效应以及误差项的方差-协方差矩阵:

然后分别估算出质量特性、测量误差以及测量值的方差-协方差矩阵:

(3)计算矩阵相应的特征值λGt和λMt(t=1,2),根据式(2)和式(3)分别计算出评价指数RPT2、PR&R2,分析测量系统能力是否足够。

4　例子分析

为了验证所提出方法的可行性,针对Voelkel[15]提供的重复性与再现性试验测得的二维数据,利用前面所提出的基于面积的方法对容差为圆的二元测量系统能力进行分析。被测质量特性的设计容差σTOL为2.6,即设计容差圆形区域的直径为2.6。

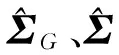
λG1=0.0059λG2=0.0987

λM1=0.0458λM1=0.1996

最后根据式(2)和式(3),计算出二元测量系统能力评价指数RPT2=0.0735,PR&R2=50.24%(α=0.05)。二元评价指数RPT2和PR&R2中的最大值PR&R2=50.24%,大于30%,表明设计容差为圆的二元测量系统能力不充分,需要对此测量系统进行质量改进。

5　结语

大多数测量系统能力分析关注的是一元质量特性，然而一些测量系统是针对二元或多元被测质量特性的。针对设计容差为圆形的二元测量系统，本文提出了一种基于面积之比的二元测量系统能力分析方法。利用测量误差和测量值分别服从正态分布的特点,根据测量误差椭圆面积与设计容差圆形面积之比和测量误差与测量值的椭圆面积之比，建立二元测量系统能力评价指数，将一元测量系统能力指数延伸到二元测量系统中，最后利用MANOVA模型进行测量系统能力分析。通过文献例子分析，验证了该方法的有效性。该方法可以延伸到设计容差为矩形或椭圆的二元测量系统中。进一步的研究包括如何对容差为圆形的二元测量系统能力指数建立置信区间等。

[1]Burdick R K,Borror C M,Montgomery D C.Design and Analysis of Gauge R&R Studies[M].Philadelphia,PA:ASA-SIAM,2005.

[2]何桢,董延峰,张敏.方差分析在复杂测量系统能力分析中的应用[J].数理统计与管理,2006,25(4):386-391.

He Zhen,Dong Yanfeng,Zhang Min.A Study on Complicated Measurement System Analysis[J].Application of Statistics and Management,2006,25(4):386-391.

[3]储晓承,叶文华,俞晖,等.基于正态模糊化方法的在机测量系统性能模糊综合评判[J].中国机械工程,2010,21(20):2424-2429.

Chu Xiaocheng,Ye Wenhua,Yu Hui,et al.Fuzzy Evaluation for Performance of On-machine Inspect System Using Normal Distribution Fuzzification Method[J].China Mechanical Engineering,2010,21(20):2424-2429.

[4]Burdick R K,Borror C M,Montgomery D C.A Review of Methods for Measurement Systems Capability Analysis[J].Journal of Quality Technology,2003,35:342-354.

[5]Li M H C,Al-Refaie A.Improving Wooden Parts’ Quality by Adopting DMAIC Procedure[J].Quality and Reliability Engineering International,2008,24:351-360.

[6]Woodall W H,Borror C M.Some Relationships between Gage R&R Criteria[J].Quality and Reliability Engineering International,2008,24:99-106.

[7]Erdmann T P,Does R J,Bisgaard S.Quality Quandaries:a Gauge R&R Study in a Hospital[J].Quality Engineering,2010,22:46-53.

[8]Nachtsheim C J,Becker K E.When is R2Appropriate for Comparing Customer and Supplier Measurement Systems[J].Quality and Reliability Engineering International,2011,27:1025-1031.

[9]Deldossi L,Zappa D.Confidence Intervals for Variance Components in Measurement System Capability Studies[J].Communications in Statistics-Theory and Methods,2012,41:2932-2943.

[10]Majeske K D.Approval Criteria for Multivariate Measurement Systems[J].Journal of Quality Technology,2008,40(2):140-153.

[11]吴小芳, 何桢, 施亮星. 基于向量的多元测量系统能力评价指数[J].系统工程,2013,31(3):123-126.

Wu Xiaofang, He Zhen,Shi Liangxing.Multivariate Measurement System Capability Indices Based on Vector[J].Systems Engineering,2013,31(3):123-126.

[12]Wang F K,Chien T W.Process-oriented Basis Representation for a Multivariate Gauge Study[J].Computers and Industrial Engineering,2010,58:143-150.

[13]Wang F K,Yang C W.Applying Principal Component Analysis to a GR&R Study[J].Journal of the Chinese Institute of Industrial Engineering,2007,24:182-189.

[14]Peruchi R S, Balestrassi P P, et al.A New Multivariate Gauge R&R Method for Correlated Characteristics[J].International Journal of Production Economics, 2013, 144: 301-315.

[15]Voelkel J G.Gauge R&R Analysis for Two-dimensional Data with Circular Tolerances[J].Journal of Quality Technology,2003,35(2):153-167.

[16]Shannon S. Analysis of Two-dimensional Gage Repeatability and Reproducibility [J]. Quality Engineering, 2007, 19:29-37.

[17]Wang F K,Chern H L.Confidence Intervals for Two-dimensional Data with Circular Tolerance in a Gauge R&R Study[J].Quality & Quantity,2012,46:55-59.

[18]Automotive Industry Action Group.Measurement Systems Analysis[M].4th ed.Betroit:Automotive Industry Action Group,2010.

[19]Montgomery D C,Runger G C.Gauge Capability and Designed Experiments,Part I:Basic Methods[J].Quality Engineering,1993,6:115-135.

[20]Hubele N F,Shahriari H,Cheng C S.A Bivariate Process Capability Vector [J].Statistical Process Control in Manufacturing,1991,3:299-310.

[21]Ch’ng C K,Quah S H,Low H C.Index in Multiple Response Optimization[J].Quality Engineering,2005,17:165-171.

(编辑苏卫国)

A New Method of Evaluating Measurement System Capability for Two-dimensional Data with Circular Design Tolerances

Wu XiaofangHe ZhenShi Liangxing

Tianjin University,Tianjin,300072

In some measurement processes the measured data by a gauge are two-dimensional and the design tolerance is a circular.When there is some correlation between two measured quality characteristics,the common evaluation indices for univariate measurement system capability cannot be applied directly to analyze and evaluate the two-dimensional measurement system capability with circular tolerance.A method of constructing evaluation indices based on ratios of areas was proposed herein.The measurement system capability evaluation indices were built through the area ratio of ellipse of gauge errors and circular of design tolerance, the ellipse area ratio of gauge error and measured values.Then the common evaluation indices for univariate measurement system capability could be extended to the two-dimensional measurement system.MANOVA was used to estimate the indices to assess the two-dimensional measurement system capability.At last the proposed method was proved by an example.

measurement system capability;two-dimensional data;repeatability and reproducibility(R&R);multivariate analysis of variance(MANOVA)

2013-11-22

国家杰出青年科学基金资助项目(71225006)；国家自然科学基金资助项目(71102140);国家自然科学基金资助重点项目(70931004)

N945.16< class="emphasis_italic">DOI

：10.3969/j.issn.1004-132X.2015.09.013

吴小芳,女,1987年生。天津大学管理与经济学部博士研究生。主要研究方向为质量管理与质量工程。何桢,男,1967年生。天津大学管理与经济学部教授、博士研究生导师。施亮星,男,1977年生。天津大学管理与经济学部副教授、硕士研究生导师。