“吨的认识”教学实录与评析
2015-10-27梁万美殷之英
梁万美 殷之英

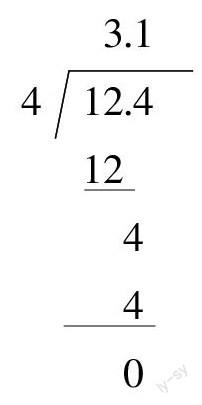
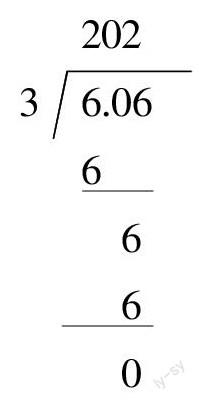
片段一:课前测试
1.根据计算过程,说说你是怎样想的?
12.4÷4=3.1
第一次商是( ),商写在( )位上。
想:因为( )个( )除以( ),够商3个( ),写在( )位上。第二次商是( ),商写在( )位上。想:因为( )个( )除以4,够商( )个( ),所以商( ),写在( )位上。
2.算一算,说一说。
6.06÷3=
[3 6.06]先算:_____;被除数中的0表示_____。
再算:_____;最后算:_____;
被除数中的第2个6表示_____。
评析:通过课前测试,了解学情,准确把握学生的数学学习起点,找到最近发展区,以便准确把握教学起点,设计、实施有效的教学过程。
片段二:解决问题,理解算理,构建算法
课件出示例1,引导学生找信息,提出数学问题,列出算式,自己先计算,再根据计算过程说说你是怎样想的?
22.4÷4=5.6 (括号里的内容是学生充分发言后填写的)
1.先确定商的位置,并找到商。第一次商是(5),商写在(个)位上。为什么?想:因为(22)个(一)除以(4),够商5个(一),所以商(5),写在(个)位上。然后算积和差,5个(一)乘4,得20个(一);22个(一)减去(20)个一,得2个(一)。
2.再次确定商的位置,准确对位,找到商。课件依次出示
思考的过程(括号里的内容是学生充分发言后填充的):
第二次商是(6),商写在(十分)位上,(商)的小数点要和(被除数)的小数点(对齐),即小数点点在(个)位的右下角,为什么?想:因为2个一和4个(十分之一)合起来是第二次的被除数24表示(24)个(十分之一),所以第二次的商6表示(6)个(十分之一)。(24)个(十分之一)除以4,够商(6)个(十分之一),商是(6),写在(十分)位上。最后算积和差,6个(十分之一)乘4,得24个(十分之一),(24)个十分之一减去24个(十分之一),得0,所以商是5.6。
评析:把问题交给学生,让学生积极动脑思考,这样既充分调动了学生的积极性,又体现了学生的主体地位,有利于培养学生勤于思考、勇于探索的学习习惯。让学生通过操作计算过程,说一说算理,理解算理,从而构建算法。
片段三:0的使用
课件出示:王鹏的爷爷计划16天慢跑14km,平均每天慢跑多少千米?
教师引导学生分析数学信息,信息一:16天,信息二:14km,问题是平均每天慢跑多少千米?两个信息之间有什么联系?(除的联系)列出算式,探究算理。(括号里的内容是学生充分发言后填写的)
14÷16=0.875
1.先确定商的位置,并找到商。第一次商是(0),商写在(个)位上。为什么?想:因为(14)个(一)除以(16),不够商1个(一),所以商(0),也就是用0来(占位),写在(个)位上;在被除数的(右下角)点上小数点,再在小数点的后面添上0,表示140个(十分之一),140个(十分之一)除以16,够商8个十分之一,(商)的小数点要和(被除数)的小数点(对齐),商的小数点点在(个)位0的右下角,类推到十分位上。第二次商(8),写在(十分位)上;然后算积和差,8个(十分之一)乘16,得128个(十分之一),140个(十分之一)减去(128)个十分之一,得12个(十分之一)。
2.添0继续除(算千分位)。课件依次出示思考过程:第三次商是(7),商写在(千十分)位上,为什么?想:因为12个十分之一表示120个(千分之一),所以在12的后面添上0,就是120个(千分之一)除以16,够商(7)个(千分之一),所以商(7),写在(千分)位上。依此类推,最后再算万分位。迁移到万分位上是5。所以14÷16的商是0.875。
评析:教师采用尝试思考、类推、迁移等解题方法,既对解题有一定的导向性,又加深了学生对算理的理解。由“整数14个一除以16不够商1个一,怎么办?”来揭示新旧认知的矛盾冲突,去激发学生的求知欲望,使探究和发现新知成为学生的心理需要。
片段四:呈错、找错、析错、纠错、避错
呈现错例,请学生们仔细观察,这位同学的做法对吗?如果不对,请你找一找错在哪里?为什么?然后帮他改一改。
1.根据计算过程,说说你是怎样想的?
12.4÷4=3.1
第一次商是(3),商写在(十)位上。想:因为(12)个(一)除以(4),够商3个(十),所以商(3),写在(十)位上。第二次商是(1),商写在(个)位上。想:因为(4)个(一)除以4,够商(1)个(一),所以商(1),写在(个)位上。
2.算一算,说一说。
6.06÷3=202
先算:6除以3,得2;
被除数中的0表示0;
再算:0除以3,得0;
最后算:6除以3,得2;
被除数中的第2个6表示6个一。
小结性提问:今后我们怎样才能避免这样的错误?
评析:教师有目的地选出学生课前测试中的错例,让学生分析,既是对算法的重新认识,又是对算理的强化认识。
总评:“除数是整数的小数除法”是小学数学教学中的一个重点,也是难点,它在计算教学中处于关键地位。本节课的教学,教师较好地把握住了教材,明确了这节课的教学地位,教学特点有:
1.充分运用了知识的类推迁移,抓住了学生知识的生长点,揭示了新问题中的新矛盾,引起学生学习的注意,激发起学习兴趣,“两主”作用发挥恰当。
2.学生学习新知是在教师的引导下先让学生练习,问题让学生自己发现,解决问题的方法让学生自己来探究,自己寻找,错例也是让学生自己分析讨论,找出错误的原因,学生在这种生动活泼的学习中掌握了知识,发展了能力,使学生学会,又会学,还乐学。
3.设计恰当,有坡度、有层次、还有变化,针对性强,利用学生的错例,进行判断、析错、纠错、避错。以防患于未然,既概括了易犯的错误,又培养了学生的辨别能力,起到了良好的巩固和强化作用。
◇责任编辑:徐新亮◇
