基于LMD与多尺度排列熵的往复压缩机故障特征提取方法

娄燕敏，胡进旭，岳磊，陈桂娟

（1.东北石油大学机械科学与工程学院，黑龙江大庆163318；2.中国石油庆阳石化公司，甘肃庆阳745002）

基于LMD与多尺度排列熵的往复压缩机故障特征提取方法

娄燕敏1，胡进旭2，岳磊2，陈桂娟1

（1.东北石油大学机械科学与工程学院，黑龙江大庆163318；2.中国石油庆阳石化公司，甘肃庆阳745002）

往复压缩机是用于压缩和输送气体的机械设备，针对其振动信号特征，提出基于LMD与多尺度排列熵的往复压缩机轴承间隙故障特征提取方法。利用具有保形特性的Hermite插值法替代传统LMD中滑动平均法构造均值与包络函数，提高LMD对非平稳信号的分解精度；以改进的LMD方法分解各状态下的振动信号，依据相关性系数筛选包含故障状态主要信息的PF分量；利用多尺度排列熵对各PF分量进行定量描述，并以平均类间样本距离对尺度因子进行优选，得出可分性良好的特征向量；利用SVM识别轴承间隙故障的类型，以识别准确率为依据，通过与不同方法所提取的特征向量进行对比，验证了方法的有效性。

往复压缩机；LMD；多尺度排列熵；轴承；故障诊断

1　引言

往复压缩机是一种用于压缩和输送气体的机械设备，其传动系统为曲柄连杆机构。长期往复重载运行势必会造成传动机构滑动轴承磨损，出现轴承间隙过大故障，致使整机振动异常，因此，对往复压缩机实施故障诊断已经势在必行。然而，由于往复压缩机的结构复杂，运动形式既有往复运动，又有旋转运动，内部激励源众多，其振动信号呈现强烈非平稳性和非线性，应用传统信号处理技术对往复压缩机进行诊断，存在一定的局限性［1，2］。

近些年来，非平稳信号自适应分解方法在故障诊断领域得到了广泛应用，而局部均值分解（Local Mean Decomposition，LMD）是英国学者Smith提出的一种新方法［3］。LMD方法通过构建局部均值与包络估计函数实现信号的分解与解调，局部均值与包络估计函数计算方法通常分为滑动平均法和极值包络线法。滑动平均法为保证光滑性需要在求解过程中进行多次平滑，这一过程可能存在相位失真，从而使分解结果产生误差［4］。极值包络线法一般分别对极大值点和极小值点采用三次样条插值构造包络线，而对于强非平稳信号，由于三次样条具有二阶导数连续特性而使包络线产生过包络和欠包络现象。相比于三次样条插值，三次Hermite插值曲线仅要求一阶导数连续，在保证曲线光滑性的同时又可以避免过包络与前欠包络现象。鉴于往复压缩机振动信号的强非平稳特性，本文采用三次Hermite插值代替三次样条插值，构造局部均值分解（LMD）的极值上下包络线。

近几年来，机械设备故障诊断更多地采用诸如样本熵、分形维数和近似熵等非线性分析方法。排列熵（Permutation Entropy，PE）是一种新兴的非线性定量描述方法，其可将自然系统中的不规则性和非线性系统以定量数值的方式呈现出来［5］，且具有计算简单，抗噪声能力强等优点。然而，类似于传统单尺度非线性参数，排列熵仍是在单一尺度上描述时间序列的不规则性。多尺度排列熵（Multiscale permutation entropy，MPE）的概念是由Aziz等提出的，可以用其衡量不同尺度下时间序列的复杂性，更具有鲁棒性［6］。然而机械系统信号随机性大，抗噪声干扰性差，单纯使用多尺度排列熵法进行信号处理，检测效果不理想。因此，多尺度排列熵与LMD结合使用，形成一种新的高性能算法，可有效提升多尺度排列熵在信号特征提取方面的有效性［7］。

针对往复压缩机振动信号特性，首先，本文利用LMD方法进行分解，获得PF分量，再以相关系数法筛选PF分量，然后，计算各PF分量的多尺度排列熵值，最后，以可分性标准优选某尺度下各PF分量排列熵值作为特征向量，实现对轴承故障特征的更有效提取。

2　LMD方法

LMD方法其实质是将任意信号分解为多个乘积函数之和。本文采用三次Hermite插值方法，构造出上下包络线，从而计算得出局部均值函数与包络估计函数。对于任意信号x（t），其分解步骤如下：

（1）找出信号x（t）的极值点序列nk，分别对极大值序列和极小值序列进行端点延拓；

（2）分别对极大值点和极小值点，应三次Hermite插值法构造上、下包络线Emax、Emin；

（3）按式（1）计算局部均值函数m11（t）及局部包络函数a11（t）

（4）分解原始信号x（t）得出局部均值函数m11（t），按式（2）计算可得h11（t）

（5）按式（3）将h11（t）除以包络估计函数a11（t），即解调h11（t），从而得出s11（t）

依据上述过程得出s11（t）的包络估计函数a12（t），若a12（t）为1时，s11（t）则为纯调频函数，若a12（t）取值非1时，则需按上述解调过程重复n次，直到a1（n+1）（t）=1，即s1n（t）此时已经为一个纯调频信号；

（6）包络估计函数a1（t）可由解调过程中产生的所有包络信号相乘获得

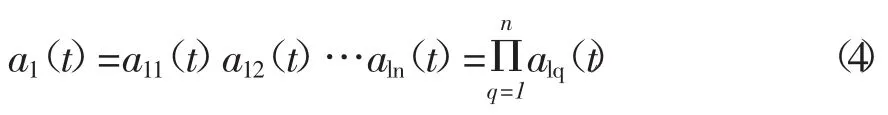
（7）包络估计函数a1（t）乘以纯调频信号s1n（t）得出了第一个PF分量

（8）从信号x（t）中减去PF1（t），即得残余信号u1（t），以其作为原始信号重复上述计算过程，经k次循环后得出单调函数uk，即

此时的原始信号x（t），已经被分解为k个PF分量和一个残余分量uk，即

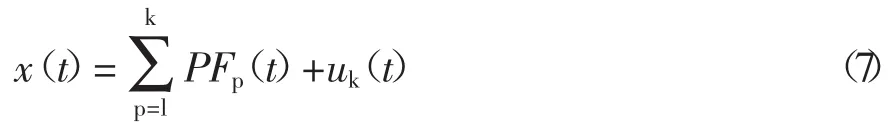
3　多尺度排列熵

3.1排列熵

设一时间序列｛X（i），i=1，2，…，N｝，对其进行相空间重构，得到矩阵

其中K——重构分量的个数

τ——延迟时间

d——嵌入维数

若以矩阵Y中的行向量为数列进行重构，则重构后的分量数目为K=N-（d-1）τ。将Y中的每行元素按照从小到大排列，每个元素所属列分别用j1，j2，…，jd表示，排列后各元素之间的大小关系可以表示为

若重构分量中有大小相等的情况，则比较jp与jq值的大小来排序，即当jp＜jq时，有x（i+（jp-1）τ）≤x（i+（jq-1）τ）。因此，重构任一时间序列获得矩阵Y，其中每行都能写出一组符号序列S（l）=｛j1，j2，…，jd｝，其中，l=1，2，…，k，且k≤m！，S（l）仅代表m！种m维相空间映射的其中一种排列。经计算得出各符号序列出现的概率P1，P2，…，Pk，则用信息熵的形式表示不同符号序列的排列熵Hp为

当Pj=1/d！时，Hp（d）就达到最大值ln（d！）。利用ln（d！）对Hp（d）进行归一化处理，则

Hp代表时间序列｛X（i），i=1，2，…，N｝的随机性，其取值可直观反映时间序列的不规则程度。

3.2多尺度排列熵

多尺度排列熵的计算步骤如下

（1）设原始序列为x（i）=｛x（1），x（2），…，x（N）｝，长度为N，预先给定嵌入维数m和时延τ，建立新的粗粒序列为

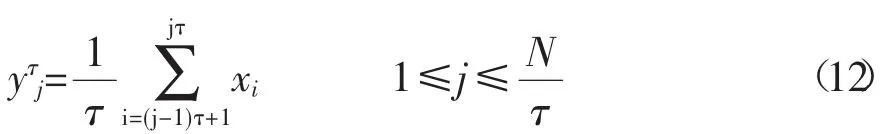
其ε=1，2，…为尺度因子。

当ε=1时，yj（1）就是原序列。对于非零的整数ε原始序列Xi被分割成N/ε个每段长为ε的粗粒序列yj（τ）；

（2）对所得到的N/ε个粗粒序列求其排列熵，并将其作为尺度因子ε的函数，称之为多尺度排列熵。

4　LMD与多尺度排列熵特征提取方法

本文首先以改进的LMD方法对轴承各状态振动信号进行分解，由于各状态分解结果中PF分量数目不一，利用与原始信号的相关系数，选择代表主要故障信息的PF分量。其次，以多尺度排列熵对LMD分解结果中的PF分量进行定量描述，最后，以各状态的最大平均类间样本距离作为标准选取某一尺度因子对应的熵值作为特征向量，形成可分性良好的特征向量。

综上所述，提出基于LMD与多尺度排列熵的特征提取方法如下：

（1）应用LMD方法自适应分解振动信号，得出每种状态信号的PF分量；

（2）计算各状态原始信号与PF分量的相关性系数，统计分析并设定适当阈值，选择能包含主要状态信息且数目统一的PF分量；

（3）计算已选定PF分量的多尺度排列熵值；

（4）依据最大平均类间距离优选尺度因子，以该尺度因子对应的排列熵值形成特征向量。

5　往复压缩机轴承间隙的故障诊断

2D12型往复压缩机是一种常用的天然气增压输送设备，轴承间隙过大故障现象往往会直接导致整机因振动超标而被迫停机，严重降低生产效率。故障实验过程中，在压缩机传动机构的一级连杆大头轴承处，利用不同程度磨损的轴瓦，分别模拟了轻度、中度和重度3种不同磨损程度的轴承间隙故障。采用ICP加速度传感器在一级十字头滑道下端采集了3种故障状态的振动信号各200组。测试过程中，数据采样频率为50 kHz，持续采集4 s。其中，轴承重度磨损的振动信号如图1所示，由图可知，轴承间隙过大，内部激励源激励强度明显增强，振动信号也随之出现大量冲击。

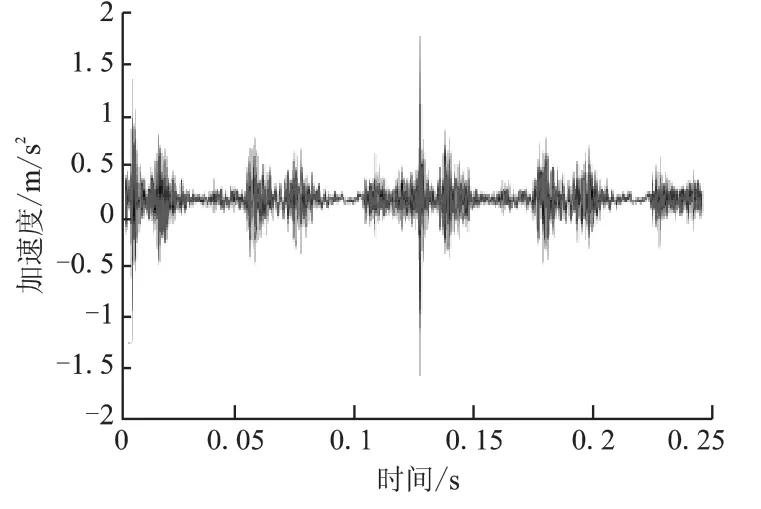
图1　重度磨损状态振动信号

采用LMD方法分别对上述3种状态信号进行分解，轻度、中度和重度磨损状态分别得出8、6和9个PF分量，计算不同故障状态下的各PF分量与原始信号的相关性系数，虽然处于不同故障状态，但每种状态振动信号分解结果中前4个PF分量基本能体现出了主要故障状态信息，其相关性系数皆大于0.15。因此，各状态均选择前4个PF分量进行分析。其中图1所示振动信号的分解结果如图2所示。

在排列熵的计算中需要设置的参数为时间序列长度N、嵌入维数m和延迟时间τ。文献［7］给出嵌入维数m的取值范围通常为3～7，若m取值过小，重构序列中状态过少，无法有效检测序列的突变性；若过大，时间序列会被均匀化，计算效率低且对序列微小变化不敏感。为了全面反映设备状态信息，本文截取两周期数据进行多尺度样本熵值计算，由于数据测试过程中50kHz采样频率所采集数据量过大，降低了了计算效率，因此对原数据进行5 kHz重采样，两周期对应的数据为1209点。时延对时间序列的计算影响较小，本文τ取1。对不同故障状态LMD分解结果中前4个PF分量进行多尺度排列熵值计算，尺度因子τ取值范围为［1，30］，经对比优选，当尺度因子ε为9时，各故障的平均类间样本距离最大，各故障状态对应的最优多尺度排列熵值如表1所示。

图2　重度磨损状态振动信号三次Hermite插值LMD分解结果

为检验该方法的有效性，分别以单一尺度的排列熵和样本熵2种指标定量描述LMD分解结果中前4个PF分量，形成特征向量，其中2种方法的各故障典型特征向量同样如表1所示。

LibSVM是林智仁教授开发的SVM工具包，现已广泛地应用于机械故障诊断识别领域［9］。本文利用该工具包进行3种特征提取方法的模式识别，以评价LMD与多尺度排列熵特征提取方法的优越性。选取轻度磨损、中度磨损和重度磨损状态下的各200组振动信号，分别以3种不同的方法提取特征向量。对于同一方法，选取每种状态120组，建立训练样本集。以LibSVM工具包训练并建立SVM模式识别器，另选取各种故障状态余下的80组特征向量建立测试样本集，对SVM进行测试，3种不同特征提取方法对应的识别结果如表2所示。

由表2可知，LMD与排列熵方法识别准确率优于LMD与样本熵方法，这是由于排列熵相对于样本熵具有抗噪声能力强，能更准确的描述设备状态信息。而LMD与多尺度排列熵特征向量识别效果又优于LMD与排列熵特征向量的识别率，验证了本文所采用方法相较于其它2种方法的优越性。这是因为，多尺度排列熵在排列熵的基础上引入了尺度因子，丰富状态信息，本文提出的尺度因子选择方法将敏感性更强的多尺度排列熵值作为特征向量，提高了识别准确率。

表1　不同特征提取方法的典型特征向量

表2　不同方法提取特征向量的识别结果

6　结论

针对往复压缩机振动信号特征，提出了基于LMD与多尺度排列熵的故障特征提取方法。利用Hermite插值构造局部均值函数与包络估计函数，提高LMD对强非平稳信号适应性，并将其应用于往复压缩机轴承故障振动信号分解，再以相关系数法筛选包含主要故障信息的PF分量，突出了状态信息。采用多尺度排列熵对各状态PF分量进行定量分析，通过对不同尺度因子对应的熵值进行优选，形成了可分性良好的特征向量。以SVM作为模式分类器诊断故障类型，与其它2种不同方法的识别结果进行对比分析，验证了本文所采用方法的有效性，在往复压缩机故障诊断领域开辟了一种新的途径。

［1］赵海洋，徐敏强，王金东.基于多重分形与奇异值分解的往复压缩机故障特征提取方法研究［J］.振动与冲击，2013，32（23）：110-114.

［2］陈桂娟，高桐，邹龙庆，等.基于ITD与排列熵的往复压缩机故障特征提取方法研究［J］.压缩机技术，2014，247：17-20.

［3］Jonathan S Smith.The Local Mean Decomposition and Its Application to EEG Perception Data［J］.Journal of the Royal Society Interface，2005，2（5）：443-454.

［4］张亢，程军圣，杨宇.基于有理样条函数的局部均值分解方法及其应用［J］.振动工程学报，2011，24（1）：97-103.

［5］Bandt C，Pompe B.Permutation Entropy：a Natural Complexity Measure for Time Series［J］.Physical Review Letters，TheAmericanPhysiologicalSociety，2002：174102（1-4）.

［6］Aziz W，Arif M.Multiscale Permutation Entropy of Physiological Time Series［C］//Proceeding of IEEE International Multi-topic Conference，INMIC，2005.

［7］郑近德，程军圣，杨宇.多尺度排列熵及其在滚动轴承故障诊断中的应用［J］.中国机械工程，2013，24（19）：2641-2647.

［8］冯辅周，饶国强，司爱威，等.排列熵算法的应用于发展［J］.装甲兵工程学院学报，2012，26（2）：34-40.

［9］赵海洋，徐敏强，王金东.改进二叉树支持向量机及其故障诊断方法研究［J］.振动工程学报，2013，26（5）：764-770.

A Fault Feature Extraction Method Based on LMD Multiscale Entropy and SVM for Bearing of Reciprocating Compressor

LOU Yan-min1，HU Jin-xu2，YUE Lei2，CHEN Gui-juan1
（1.Mechanical Science and Engineering Institute，Northeast Petroleum University，Daqing 163318，China；2.China Petroleum Qingyang Petrochemical Company，Qingyang 745002，China）

Reciprocating compressor is the machinery equipment for compressing and delivering gas，based on the non-stationary and nonlinearity characteristics of reciprocating compressor vibration signal，a feature extraction method for bearing fault of reciprocating compressor based on LMD and multiscale permutation entropy is proposed.To improve the decomposition accuracy of LMD for nonstationary signals，the cubic Hermite interpolation method is used to construct the means and envelope function instead of traditional LMD sliding average method.Vibration signals in each state are decomposed into a series of PF components with the improved LMD method，and the PF components which contain the main information of fault state were chosen according to the relative coefficient. Multiscale permutation entropy of the selected PF components was calculated，and the optimized scale factor was selected based on the maximum of average distances between different states，so the eigenvectors which have the best divisibility were extracted.Taken SVM as pattern classifier，the type of bearing clearance fault was diagnosed，and superiority of this method is verified by comparing the eigenvectors extracted by LMD and permutation entropy and LMD and sample entropy method.

reciprocating compressor；LMD；multiscale permutation entropy；bearing；fault diagnosis

TH457

A

1006-2971（2015）04-0006-05

2015-02-05