浅谈数学教学中创造性思维的培养

黄国松

摘 要：数学教学应该让学生在数学活动中充分发挥他们的想象，鼓励探索，培养创新精神，让他们成长为充满自信、积极进取、富有创造力的现代人。就如何培养学生的创造性思维谈点滴体会。

关键词：创造性思维;挖掘;培养

一、精心创设问题情境，诱发学生思维积极性

数学思维是数学教学的核心，创设良好的思维情境，能激发学生探求数学奥秘的欲望，从而调动学生积极思维，为思维训练铺设良好的通道。

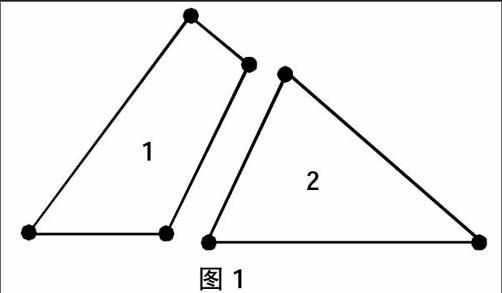
如，在学习三角形全等时，可以先讲这样一个实例，我们有一块三角形玻璃被打碎成两半（如图1），现在我要上街配一块与原来一样大小的三角形玻璃，要不要将两块玻璃都拿去？

学生：有的说带一块，有的说带两块。

教师：（先让学生讨论片刻）其实，只带一块就可以了，大家想一想，应该带其中哪一块，为什么？

经过教师的启发，学生的思路被打开，这样就为学习全等三角形的判定创设了思维情境，激发起学生的思维。

教师在创设问题情境时，一定要紧扣课题，不要故弄玄虚，离题太远，衡量问题情境设计好坏的标准，一是有利于激发学生思维的积极性;二是直接有利于当前所研究课题的解决。

二、培养思维广阔性

思维的广阔性是指思路宽广，善于多角度、多层次地进行探求。在数学学习中，思维的广阔性表现为既能把握数学问题的整体，抓住其基本特征，又能抓住重要的细节和特殊因素放开思路进行思考，使他们思路开阔，处于一种主动探索的心理状态，通过活跃的思维达到求异、求佳、求新。具体做法：教师要有计划、有目的地设计一些问题，如，一题多解、一题多变、一题多用等习题，开拓学生思路，逐渐培养学生形成思维的广阔性品质。

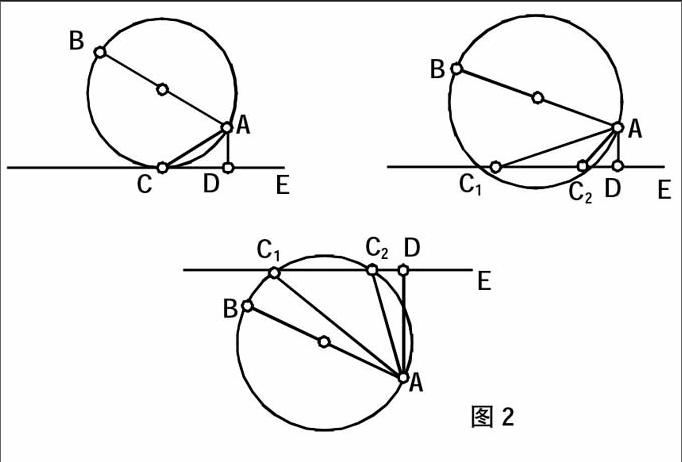
例如，如图2，AB是☉O的直径，AD⊥CE于D，CE切☉O于点C。

（1）求证：AC2=AD·AB

（2）若把直线CE向上平移与☉O交于C1、C2，在其他条件不变的情况下，问是否存在与（1）有相似的结论，若存在，请证明，不存在，请说明理由。

问题一提出，学生跃跃欲试，勇于探索。

答案：（1）略，（2）存在AB·AD=AC1·AC2，证明略。

三、重视逆向分析，培养思维的灵活性

思维的灵活性是指思维活动的反应速度，它表现为迅速地发展、分析和处理问题。有些问题，正面思维很难解决问题，但采用逆向思维时，问题就会迎刃而解，特别是在数学逻辑性较强的学科中，逆向思维就越显得很重要。

例如，将抛物线y=ax2+bx+c向左平移2个单位，再向下平移3个单位，得到一新抛物线y=2x2+8x+3，试确定a、b、c的值。

分析：这题目按图象变化进行思考，运算复杂且有相当难度，若能从结论出发进行逆向推理，则简单易解，即将y=2x2+8x+3=

2（x+2）2-5（结论）向右平移2个单位再向上平移3个单位得原抛物线（已知），然后利用比较系数法确定原解析中的a、b、c值。

数学知识有许多“相反互逆”的概念、公式、法则和定理，教学中要恰当地引导学生对它们进行双向思考，夯实这些数学知识，无疑会提高学生的逆向思维能力。

四、鼓励学生猜想，培养直觉思维能力

直觉思维要求有一定的依据，但又不苛求有充分的依据，这就等于放宽了条件，既符合学生的思维习惯，又不至于过早筛掉可能有用的信息。直觉思维具有快速性，迅速肯定或否定某一思路结论，给人以“发散”“放射”的感觉，一计不成又生一计。因此，加强直觉思维能力的训练，对克服思维的单向性，提高思维品质是有利的。它是学习数学与创造数学必不可少的思维形式。

例如，圆内接四边形的边长依次为25、39、52和60，这个圆的直径是（  ）

A.62 B.63 C.65 D.69

先要求学生猜出可能的答案，有的学生可能回答应选（C）。教师：为什么？学生：65、25、60都是5的倍数，这是一种直觉，根据这个直觉作出（C）是正确答案的判定，理由是不充分的，但优先考虑（C）却是合理的。果然，65=5×13，25=5×5，60=5×12它是一组勾股数，所以选（C）是正确的。

要培养学生的思维能力，教师必须具备思维品质，必须更新教育观念，下决心树立终身学习的观点，用自己的聪明才智点燃学生心灵中的思维火花，以此推动学生不断发现新问题。

·编辑 张珍珍