一类二阶变系数微分方程的通解

程 国，丁正生

（1.商洛学院数学与计算机应用学院，陕西商洛726000；2.西安科技大学理学院，陕西西安710054）

一类二阶变系数微分方程的通解

程 国1，丁正生2

（1.商洛学院数学与计算机应用学院，陕西商洛726000；2.西安科技大学理学院，陕西西安710054）

求解二阶变系数微分方程一般比较困难，没有通用的方法。根据一类二阶变系数非线性微分方程的特点，通过变量代换转化为可降阶的微分方程，再应用一阶微分方程的解法给出其通解公式，并在此基础上给出了一个推论。

变系数；微分方程；通解

研究二阶线性微分方程

在理论上和应用上都有着非常重要的意义。由于二阶线性微分方程与黎卡提（Riccati）方程的求解具有等价关系，而Liouville于1841年就证明了Riccati方程一般无初等解，因此式（1）的通解没有普遍的解法。关于式（1）的通解结构文献［1］中给出了完整的结论。文献［2-9］分别讨论了一些特殊的二阶变系数微分方程的求解方法，已取得了一些成果。本文研究了一类二阶变系数非线性微分方程

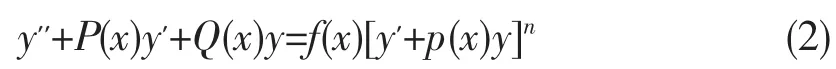
的通解求法，其中P（x），Q（x），f（x）都是x的连续函数。并在n=0时得到了一系列二阶变系数非齐次线性微分方程及其通解公式。

1 预备知识

本文中使用的术语、记号参考文献［1］，不定积分表示被积函数的一个确定原函数，不含积分常数。

引理1［10］一阶线性微分方程的通解是

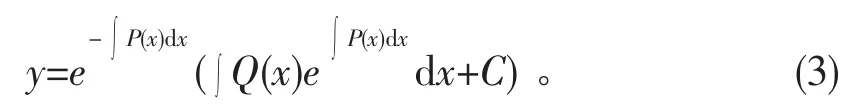
引理2［10］可分离变量微分方程）的通解是

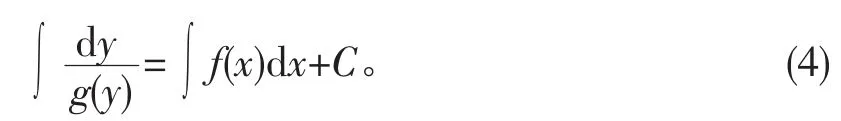
2 主要结果及其证明

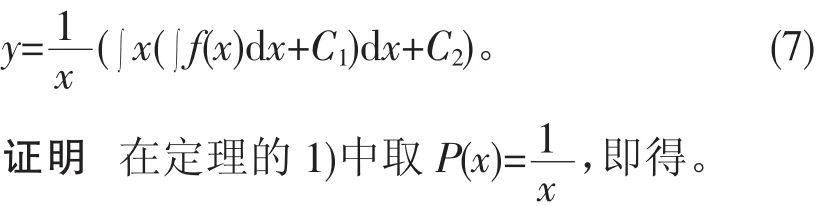
3 应用举例

［1］同济大学数学系.高等数学［M］.6版.北京：高等教育出版社，2007：325-328.

［2］刘琼.一类二阶变系数微分方程的解［J］.广西右江民族师专学报，2002，15（6）：18-20.

［3］裴东林.关于一类微分方程初等解法的讨论［J］.甘肃教育学院学报：自然科学版，2003，17（3）：7-9.

［4］曹根牛.二阶变系数齐次线性微分方程与黎卡提方程［J］.西安科技学院学报，2004，24（2）：247-249.

［5］胡劲松，李先富，郑克龙.一种二阶变系数线性微分方程的求解方法［J］.重庆工商大学学报：自然科学版，2005，22（3）：220-222.

［6］梁洪亮，徐华伟.一类二阶变系数常微分方程的可积条件［J］.数学的实践与认识，2007，37（23）：157-160.

［7］张新丽.一类二阶变系数线性微分方程的新解法［J］.科学技术与工程，2009，9（14）：4102-4103.

［8］范小勤，毕朝晖.几类二阶变系数微分方程的求解［J］.大学数学，2011，27（3）：200-203.

［9］张玉兰.一类二阶变系数线性微分方程的通解［J］.佳木斯大学学报：自然科学版，2013，31（4）：638-640.

［10］化存才，赵奎奇，杨慧，等.常微分方程解法与建模应用选讲［M］.北京：科学出版社，2009：5-15.

（责任编辑：李堆淑）

General Solution to One Class Second Order Differential Equations with Variable Coefficients

CHENG Guo1，DING Zheng-sheng2

（1.College of Mathematics and Computer Application，Shangluo University，Shangluo 726000，Shaanxi；
2.College of Science，Xi'an University of Science and Technology，Xi'an 710054，Shaanxi）

The solution of second order differential equation with variable coefficients is generally difficult，and there is no universal method.Based on the characteristics of a class one second order nonlinear differential equation with variable coefficients，by variable substitution into reduced order differential equation，the general solution is given to the application of solution of first order differential equations，and on this basis，a corollary is proposed.

variable coefficient；differential equation；general solution

O175.1

A

1674-0033（2015）04-0005-02

10.13440/j.slxy.1674-0033.2015.04.002

2015-02-19

陕西省教育厅专项科研计划项目（2013JK0597）

程国，男，甘肃张掖人，硕士，讲师