调和指标的极值图
2015-10-26王晓汪小黎
王晓,汪小黎
(商洛学院数学与计算机应用学院,陕西商洛726000)
调和指标的极值图
王晓,汪小黎
(商洛学院数学与计算机应用学院,陕西商洛726000)

调和指标;极值图;Split图
设G=(V(G),E(G)),表示一个图,其中V(G)和E(G)分别表示G的顶点集和边集。对于u∈(V(G),d(u))表示顶点u的度,度为1的顶点称为叶子点。若图G的顶点集的子集A的导出子图G[A]是空图,则称A为G的独立集;若G[A]是完全图,则称A为G的团。其他本文中涉及到概念参阅文献[1]。
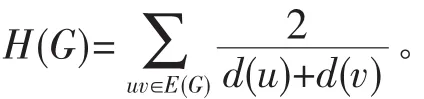
一个图称为Split图[10],如果它的顶点集能划分为一个团和一个独立集。用Sp,q表示顶点集划分为阶为p的团和阶为q的独立集的Split图。本文中首先利用图的调和指标的另一种表述形式,对非空正则图的调和指标进行研究,然后利用文献[3]中的一个引理,证明了固定团数和独立集阶数的Split图的调和指标的下界,并给出相应的极图。
1 正则图的调和指标
文献[5]中给出了最小度δ(G)≥k的图G的调和指标的另一种表述形式,并证明了不含三角形的图的调和指标的下界。这里,首先给出一般图G的调和指标的另外一种表述形式。设G是阶为n的图,mij表示图G中两个端点的度数分别为i和j的边的数目,则有

在文献[3]中,给出固定阶数的简单连通图的调和指标的下界。
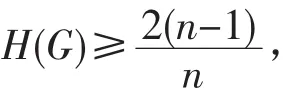
结合定理1和定理2,有如下定理。
2 Split图的调和指标

[1]Reinhard D.Graph theory(Second Edition)[M]. Hongkong:Springer-Verlag,2000:95-122.
[2]FajtlowiczS.OnconjecturesofGraffiti-II[J].CongrNumer,1987,60:187-197.
[3]Zhong L.The harmonic index for graphs[J].Applied Mathematics Letters,2012,25(2):561-566.
[4]Zhong L.The harmonic index on unicyclic graphs[J]. Arc Combinatoria,2012,104:261-269.
[5]Liu J.On the harmonic index of triangle-free graphs[J]. Applied Mathematics,2013,4(8):1204-1206.
[6]王晓,段芳.单圈图的解析[J].华东师范大学学报:自然科学版,2009,143(1):13-21.
[7]Deng H,Balachandran S,Ayyaswamy S K,et al.Note:On the harmonic index and the chromatic number of a graph[J].Discrete Applied Mathematics,2013,161:2740-2744.
[8]陈锦丽.具有k个悬挂点的仙人掌图的调和指标[J].闽南师范大学学报:自然科学版,2014,84(2):7-11.
[9]Chen J,Lv J.On the harmonic index of cacti[J]. InternationalJournalofAppliedMathematicsand Statistics,2014,52(1):72-83.
[10]Maffray F,Preissmann M.Linear recognition of pseudo-split graphs[J].Discrete Applied Mathematics,1994,52(94):307-312.
(责任编辑:李堆淑)
The Extremal Graphs for Harmonic Index
WANG Xiao, WANG Xiao-li
(College of Mathematics and Computer Application,Shangluo University,Shangluo726000,Shannxi)
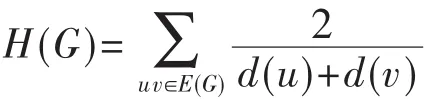
harmonic index;extremal graphs;Split graph
O157.5
A
1674-0033(2015)04-0003-02
10.13440/j.slxy.1674-0033.2015.04.001
2015-04-16
商洛学院科研基金项目(12SKY011)
王晓,男,河南南阳人,硕士,讲师
