构造奇数阶空间完美幻立方及空间对称完美幻立方的三步法

詹森，王辉丰

（1.广东技术师范学院计算机科学系，广东广州510665；2.海南师范大学数学与统计学院，海南海口571158）

构造奇数阶空间完美幻立方及空间对称完美幻立方的三步法

詹森1，王辉丰2

（1.广东技术师范学院计算机科学系，广东广州510665；2.海南师范大学数学与统计学院，海南海口571158）

文章给出构造奇数n=2m+1（m为m≠3t+1且m≠5t+2，t，s=0，1，2，…的自然数）阶空间完美幻立方和空间对称完美幻立方的三步法，得到（n！）3个不同的n阶空间完美幻立方和（22m（m！））3个不同的n阶空间对称完美幻立方.

幻立方；空间完美幻立方；空间对称完美幻立方；余函数；三步法

人们知道，研究空间（三维）幻立方比平面（二维）幻方更复杂、更困难.文［1-8］研究了各种平面幻方，文［9～10］讨论了空间幻立方，提出了各类空间幻立方的构造方法，得到一些新结果.

如果一个空间幻立方的四条空间对角线及与其同方向的空间泛对角线上的n个数字之和也都等于n阶幻立方常数，则称之为空间完美幻立方.空间对称的空间完美幻立方则称为空间对称完美幻立方.本文将给出奇数阶空间完美幻立方和空间对称完美幻立方的构造方法及其证明.为此，首先根据文［8］中的余函数r（t）（对任意给定的整数E）有以下预备定理（略去证明）.

1　预备定理

下面阐述构造奇数n=2m+1（m为m≠3t+1且m≠5s+2，t，s=0，1，2，…的自然数）阶空间完美幻立方（简称完美幻立方，下文均如此）的步骤.

2　构造奇数阶完美幻立方的步骤

对所要构造奇数阶完美幻立方，与文［9］一样，仍设以k轴为法向的第k（k=1，2，…，n）个截面的i行、j列元素为c（k，i，j），其基方阵i行、j列元素为b（k，i，j）.其构造方法是：

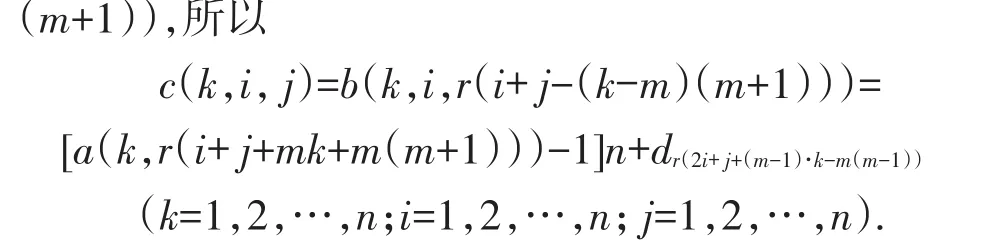
k个从小至大的数字（截面）顺序组成的立方阵C就是所要构造的奇数阶完美幻立方（见定理1）.以上三步称为三步法.

定理1数字立方阵C是一个奇数n=2m+1（m为m≠3t+1且m≠5s+2，t，s=0，1，2，…的自然数）阶完美幻立方.

证明证明如下

1）数字立方阵C以k轴为法向的k（k=1，2，…，n）个截面，每行，每列上n个数字的和都是常数

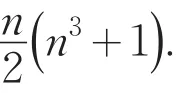
事实上，根据预备定理4，第j（j=1，2，…，n）个截面上，其第i（i=1，2，…，n）列上n个数字之和为

3　定理1及证明

综上所述，数字立方阵C是一个奇数n=2m+1（m为m≠3t+1且m≠5s+2，t，s=0，1，2，…的自然数）阶空间完美幻立方.证毕.

4　构造奇数阶空间对称完美幻立方的步骤

第一步按文［8］构造n×n基方阵A.A位于第i行、第j列的元素为a（i，j）（i，j=1，2，…，n），于基方阵A是一个中心对称方阵，有

第二步与构造完美幻立方步骤的第二步相同，但要求dn=m+1，dt+dn-t=n+1（t=1，n-1）.

第三步与构造完美幻立方步骤的第三步相同.所得数字立方阵C就是一个奇数n=2m+1（m为m≠3t+1且m≠5s+2，t，s=0，1，2，…的自然数）阶对称完美幻立方（见定理2）.以上步骤称为构造奇数阶空间对称完美幻立方（简称对称完美幻立方）的三步法.

5　定理2及证明

定理2数字立方阵C是一个奇数n=2m+1（m为m≠3t+1且m≠5s+2，t，s=0，1，2，…的自然数）阶对称完美幻立方.

证明由定理1，只需证明数字立方阵C是空间中心对称的即可.事实上，有

的自然数所组成，其中a（i，j）（i，j=1，2，…，n）是1～n2的自然数，因此，以上两种幻立方都是由1～（n2-1）n+ n=n3的自然数所组成，即它们是正规的幻立方.

构造完美幻立方步骤第一步中基方阵A有（n！）2不同的选择，其第二步各列基数及随后共n个数的安装顺序有n！种不同的选择，所以按该构造法可得出（n！）3个不同的奇数n=2m+1（m为m≠3t+1且m≠5s+2，t，s=0，1，2，…的自然数）阶空间完美幻立方.

构造对称完美幻立方步骤第一步中基方阵A有（2m（m！））2不同的选择，其第二步各列基数及随后共n个数的安装顺序有2m（m！）种不同的选择，所以按该构造法可得出（2m（m！））3个不同的奇数n=2m+1（m为m≠3t+1且m≠5s+2，t，s=0，1，2，…的自然数）阶对称完美幻立方.

例用以上三步法构造一个7阶对称完美幻立方.

第一步根据文［9］构造一个7阶对称完美幻方的基方阵：

第三步将Bk（k=1，2，…，7）的第i行（i=1，2，…，7）的元素右移r（（k-m）（m+1）-i）个位置，右移后得到的分别记为C1，C2，…，C7，由以上定理2知，所得的是7阶对称完美幻立方：

［1］詹森，王辉丰.关于构造高阶幻方的新方法［J］.海南师范大学学报：自然科学版，2009，22（3）：250-254.

［2］詹森，王辉丰.奇数阶对称完美幻方的构造方法［J］.海南师范大学学报：自然科学版，2009，22（4）：396-402.

［3］王辉丰，詹森.关于构造三类奇数阶幻方的新方法［J］.海南师范大学学报：自然科学版，2010，23（1）：12-15.

［4］詹森，王辉丰.构造镶边幻方的代码法［J］.海南师范大学学报：自然科学版，2010，23（2）：152-157.

［5］王辉丰.构造镶边幻方代码法的代码公式［J］.海南师范大学学报：自然科学版，2012，25（3）：269-273.

［6］詹森，王辉丰.构造奇数阶对称幻方及奇偶数分开对称幻方的新方法［J］.海南师范大学学报：自然科学版，2011，24（4）：395-399.

［7］王辉丰.构造奇数阶完美幻方和对称完美幻方的两步法［J］.海南师范大学学报：自然科学版，2012，25（1）：28-31.

［8］詹森，王辉丰.构造奇数阶幻方，完美幻方和对称完美幻方的新方法［J］.海南师范大学学报：自然科学版，2011，24（3）：265-269.

［9］詹森，王辉丰.构造奇数阶对称幻立方及对称完美幻立方的三步法［J］.海南师范大学学报：自然科学版，2013，26（3）：266-273.

［10］詹森，王辉丰.构造双偶数阶空间更完美幻立方的四步法［J］.海南师范大学学报：自然科学版，2014，27（4）：125-131.

责任编辑：黄澜

Three Footwork's Structure Methods about Odd Order Space Perfect Magic Cube and Space Symmetrical Perfect Magic Cube

ZHAN Sen1，WANG Huifeng2
（1.Department of Computer Science，Guangdong Technical Normal University，Guangzhou 510665，China；2.College of Mathematics and Statistics，Hainan Normal University，Haikou 571158，China）

Three footwork's structure methods and their theoretical proofs.were Given.When n=2m+1（m is m≠3t+1 and m≠5t+2，t，s=0，1，2，…natural number），these methods may obtain（n！）3different n order space perfect magic cube and（22m（m！））3different n order space symmetrical perfect magic cube.

magic cube；space perfect magic cube；space symmetrical perfect magic cube；residual function；three footwork method

O 157.6

A

1674-4942（2015）04-0375-06

2015-09-15