考虑频率约束的孤网风电渗透率极限评估

刘建平，吴锡昌，王旭斌，吴岩，王忠为，张洪力，刘文

（1．中电投蒙东能源集团有限责任公司，内蒙古通辽市　028011；2.华北电力大学电气与电子工程学院，北京昌平　102206）

考虑频率约束的孤网风电渗透率极限评估

刘建平1，吴锡昌2，王旭斌2，吴岩1，王忠为1，张洪力1，刘文1

（1．中电投蒙东能源集团有限责任公司，内蒙古通辽市028011；2.华北电力大学电气与电子工程学院，北京昌平102206）

大规模具有间歇性、波动性且难以预测的风电接入孤立电网后将会给其频率稳定性带来一系列挑战，以中电投霍林河循环经济示范工程孤立电网为背景，将风电波动视为平稳随机过程并采用平均功率谱密度提取大量风电波动信息，不借助商业软件建立了考虑频率约束的风电渗透率极限评估模型。基于该模型计算了在频率稳定约束下霍林河孤网系统最大风电消纳能力，从而为电网规划提供指导。最后，对不同类型的机组频率响应能力进行分析，考虑增建一部分燃气电站提高电网的风电消纳能力。也为电网后续升级和建设提供了参考依据。

风电渗透率；频率稳定；功率谱密度；一次调频；风电消纳

风力发电作为可再生能源中成本较低、技术较成熟、可靠性较高的新能源，近年来发展快速。内蒙古是我国风能资源最丰富的省区，风能总储量8.9亿kW，技术可开发容量1.5亿kW，占全国陆地风电可开发容量的50%，现并网风电装机达到760万kW［1］，但是由于这些地区远离负荷中心、电源结构单一、缺乏调峰调频能力以及跨区域输电能力不足，导致已开发资源存在弃风限电现象。同时，蒙东地区作为电解铝主要产业区，因发展电解铝而耗用的大量煤炭以及产生的大气污染物给节能减排带来了巨大压力，使得电解铝发展受到抑制。显然，蒙东地区的风电和电解铝两种产业都遇到了阻碍，处于两难境地。中电投蒙东能源集团率先提出发展循环经济产业链［2］，力主通过大规模风电就地消纳实现电解铝产业清洁发展。

这一构想实现的关键是风电在孤立电网内的消纳问题。关于电力系统的风电消纳能力，目前尚无明确统一的定义［3］。现有研究多以风电渗透率极限作为系统对风电的消纳能力，风电渗透率通常又可分为装机渗透率和能量渗透率。风电装机渗透率是指风机安装容量占最大负荷的百分比，风电能量渗透率是指风力发电全年提供的电量占系统负荷全年耗电总量的百分比。然而由于部分风电机组可能处于弃风停运状态，风电装机渗透率极限并不能真实地反映系统对风电的消纳能力，因此本文取风电能量渗透率极限作为衡量系统风电消纳能力的标准，简称风电渗透率极限。风电渗透率极限是指不导致系统出现异常情况下风力发电全年提供的电量占系统负荷全年耗电总量的最大比例。它从全电网角度出发，目的在于确定风电对系统频率稳定的影响。风电渗透率极限的确定，无论从节能减排角度考虑还是从风电场安全运营角度考虑都有着非常实际的研究意义［4］。

孤立电网又称孤网，一般泛指脱离大电网的小容量电网，即孤立运行的机网容量比大于8%的电网。孤网运行最突出的特点［5］，是由负荷控制转变为频率控制，要求调速系统具有负荷要求的静态特性、良好的稳定性和动态响应特性，以保证在用户负荷变化的情况下自动保持电网频率稳定性。然而，由于孤网运行机组数量少、容量小、稳定性差，往往会造成系统频率大幅波动，因此频率稳定问题成为限制大规模风电就地消纳的主要障碍［6］。文献［7-8］对风电场进行建模，并通过实际电网对含大容量风电场的电网进行动态仿真分析。文献［9-12］针对某地区孤立电网，利用PSS/E、PSCAD、BPA等电力系统仿真平台，通过动态仿真的方式，研究大规模风电集中接入对该孤立电网暂态稳定的影响。文献［13-14］基于时频转换方法建立了风电波动对电力系统频率稳定影响评估模型，该方法相比于时域仿真，具有计算速度快，评估结果接近实际的优点。文献［15，4］分别讨论了风电功率渗透率对系统动态频率特性的影响以及风电渗透率的几种计算方法，其中，风电功率渗透率是按照风电的装机渗透率来进行计算的，并未讨论风能占实际负荷的比重对系统频率特性的影响。

为此，本文以霍林河循环经济孤立电网为背景，将风电波动视为平稳随机过程，采用平均功率谱密度（power spectral density，PSD）提取大量风电波动信息，不借助商业软件，建立了考虑频率约束的孤立电网风电渗透率极限评估模型。利用该模型评估在频率稳定约束下霍林河孤网系统最大风电消纳能力，为探索霍林河孤网中合适的频率控制策略提供依据。最后，对比分析不同类型的机组频率响应特性，为电网后续升级和建设提供了参考依据。

1　霍林河循环经济示范工程孤立电网概况

霍林河循环经济示范项目是我国首个高载能产业大规模清洁能源利用示范项目，是以露天煤业4 000万t褐煤产能为基础，在已建成8台共120万kW自备火电机组的基础上，“上大压小”新建2台35万kW超临界空冷燃用劣质煤火电机组、80万kW风电以及配套局域网，向霍煤鸿骏78万t电解铝负荷供电，实现发电、用电自给自足，构建高载能产业清洁化发展示范区。

霍林河循环经济孤立电网属于相对独立的小型电网，预计2016年建成投产。图1所示为霍林河循环经济孤立电网系统规划结构图。规划建成后，自备火电机组8台，总装机容量1 800 MW；新建2个风电场，风电场内风机集中分布，相关性较强，总装机容量800 MW；孤立电网内主要负荷为电解铝直流负荷，用电负荷需求总计1 400 MW。

图1　霍林河循环经济孤立电网系统结构图Fig.1　Framework of the recycling economy isolated power system in Huolinhe area

大规模具有间歇性、波动性且难以预测的风电接入该局域电网后将会给其频率稳定性带来一系列挑战，该孤网调频系统存在如下特点。

1）电网内尚未建立自动发电控制系统（automatic generation control，AGC），系统频率调整主要靠发电机调速器和转子惯性响应，电网调度周期为10 min。

2）孤网建成后，与外界大电网没有任何功率交换，完全依靠网内传统发电机组提供调频支持。

2　考虑并网风电随机特性的系统频率稳定评估模型

图2所示为电网频率波动评估过程示意图。该评估过程可以分为3步：风电场功率输出仿真、电网频率偏差计算、频率波动统计分析。通常，数值天气预测系统（numerical weather prediction，NWP）可以精确地预测出未来5～15 min内的平均风速Vw0和标准差σw［16］。该评估模型可以利用预测的风速数据精确计算出下一调度周期内（10 min）的频率波动最大值。

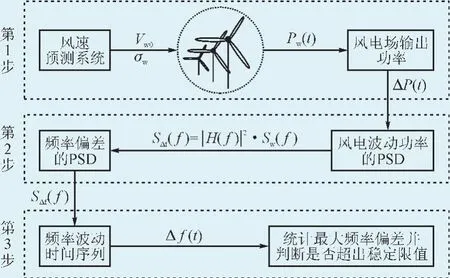
图2　电网频率波动评估过程示意图Fig.2　Flow of the assessment of grid frequency deviation

2.1风电场功率输出仿真

图3所示为风电场功率波动频域仿真模型［17-18］。该模型能够根据预测风速快速仿真出下一调度周期的秒钟级别的风电功率输出Pw（t）。其中风电场风机轮毂处风速波动的PSD由式（1）可以计算得到。考虑到风机集中分布，可以近似认为Shub［1］=Shub［2］=…=Shub［N］。γ［r，c］（f）为相关矩阵，该矩阵计及了风电场的平滑作用，将风机间功率波动的互补性进行了量化。

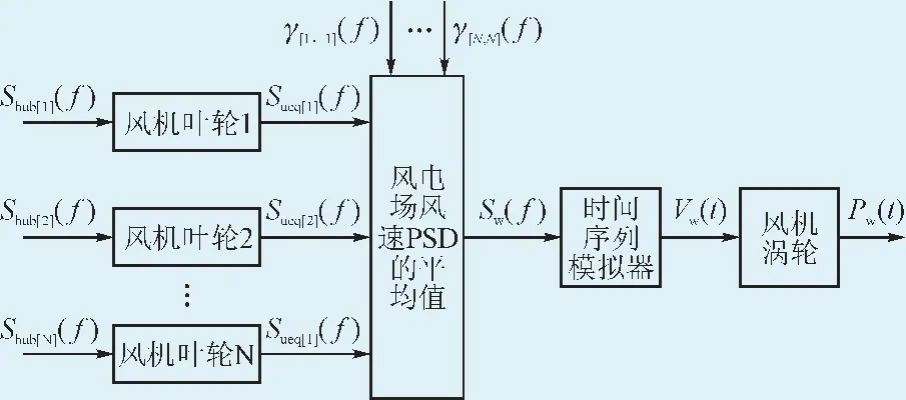
图3　风电场功率输出频域仿真模型Fig.3　Simulation of wind farm power output based on frequency domain

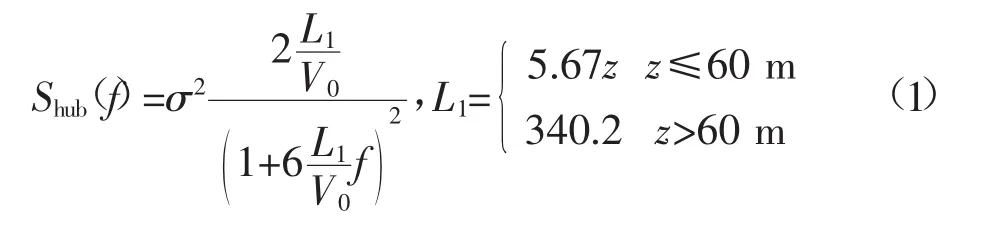
式中：z为风机轮毂离地高度。

一个调度周期内风电功率的平均功率Pave（t）在电网中通过调度方式响应，主要影响电网频率波动的是风电功率的高频分量ΔPw（t），此分量为风速变化引起的功率波动，往往通过电网内机组自动发电控制、调速器、转子惯性进行响应，计算公式如下：

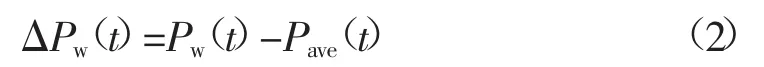
2.2考虑并网风电波动的频率偏差计算

实际电网中，每个调度控制周期对最大频率波动偏差评估一次。为了对风电波动扰动下的频率控制和分析，通常忽略对电压和功角的动态特性研究，负荷频率响应模型使用简化的低阶线性模型［19］，如图4所示。其频率响应传递函数G（s）见附录A。

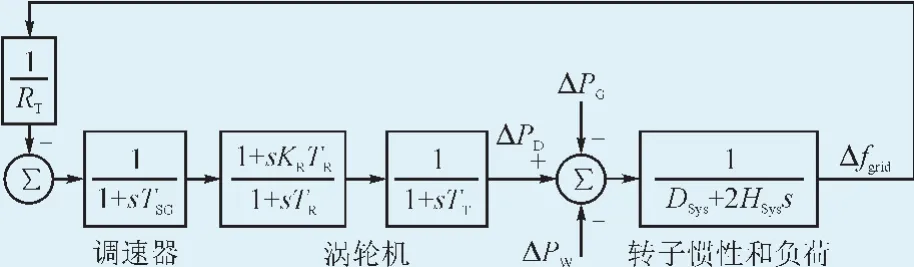
图4　负荷频率响应模型Fig.4　Load frequency respond model

国内外研究风电波动对电网调频的影响主要基于电力系统时域仿真软件，如Power Factory、PSS/E等，但是当系统规模较大时，在一个调度周期内难以依靠商业软件完成频率偏差评估计算。然而，基于PSD的频率响应评估模型根据风电波动功率ΔPW（t）和电网频率响应特性，可以很快的计算出下一个调度周期内频率波动情况［14，21］。基于PSD的频率响应评估计算过程为：

（1）对风电波动功率序列ΔPW（t）进行傅里叶变换，计算风电波动功率的功率谱密度Sw（f）。

（2）基于维纳-辛钦（Wiener-Khinchine）定理［20］，通过式（3）计算电网频率偏差的功率谱密度SΔf（f）。

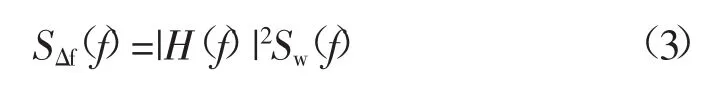
式中：|H（f）|为系统频率响应的幅值，并且|H（f）|与系统频率响应传递函数G（s）存在如下关系：

（3）计算电网频率时域时间序列Δfgrid（t）

首先，通过式（4）和式（5）计算Δfgrid（t）的傅里叶变换序列，然后通过傅里叶逆变换求出Δfgrid（t）。

式中：E（·）为期望函数；δ（f）为关于频率f的随机复数矩阵。

2.3频率波动统计分析

累积曲线是一种直观简洁的统计分析工具，如图9所示。其计算方法是将计算的频率偏差按降序排列，高于或等于指定频率波动限值的频率偏差个数作为对应的横坐标，纵坐标为指定频率波动限值。因此，对应给定频率偏差的横坐标为超出频率约束的时间百分比。

衡量频率稳定的主要指标是频率波动最大值。为了提高统计分析的可信度，设定时间百分比1%对应的频率偏差为本调度周期内的最大频率波动值（图9中A、B点）。

3　基于频率约束的最大风电渗透率评估

高渗透率的风电接入孤立电网将使电网频率偏差超出允许波动范围，为了电网稳定运行，部分风电机组不得不被迫停止出力，从而降低风电功率波动和电网频率波动。图5为基于频率约束的最大风电渗透率评估过程示意图。值得注意的是，虽然系统频率稳定评估模型是基于预测风速计算下一调度周期的频率偏差最大值，但是计算过程中基于统计方法取累积时间百分比1%作为最大频率波动值，所以同样适用于基于历史风速（时间长度包含数万甚至数十万个调度时间周期）数据用来评估整个电网的频率响应能力。首先，假设电网风电渗透率为100%，通过对很长一段时间内数以万计的调度周期内频率偏差统计分析，得出电网的最大频率偏差，与频率波动限值进行比较，如果不满足电网的频率稳定要求，则减小风电渗透率，重新计算电网最大频率偏差，直到满足频率稳定要求，此时的风电渗透率即为不导致系统出现异常情况的最大风电渗透率。

图5　最大风电渗透率评估过程示意图Fig.5　Flow of the assessment of maximum wind power penetration

4　系统仿真及结果

4.1不同风电渗透率下电网频率稳定评估

假设霍林河地区下一个10 min时间段内预测风速平均值Vave=10 m/s，相对标准差σw=15%，则基于频域的风电场秒钟级等效风速仿真输出变化曲线如图6所示。再利用风电机组功率特性曲线便可以将等效风速随机序列Vw（t）转化为整个风电场的波动功率输出Pw（t）。

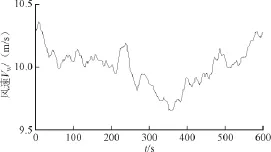
图6　风速Vw仿真曲线（对应Vave=10 m/s，σw=15%）Fig.6　Simulation of wind corresponding to Vave=10 m/s，σw=15%

图7　功率谱密度Sw（f），|H（f）|，SΔf（f）Fig.7　Sw（f），|H（f）|，SΔf（f）

图7所示为孤网频率偏差计算过程中风电功率波动功率谱密度Sw（f）、孤网频率响应的功率谱密度|H（f）|以及孤网频率波动功率谱密度SΔf（f）的计算结果。图7计算过程中分别考虑两种不同风电渗透率，系统频率响应不变，其中虚线为风电渗透率为10%对应的计算结果，实线为风电渗透率为20%对应的计算结果。

从图7可以看出，当风电渗透率越高，风电功率波动功率谱密度在各个频率幅值越大，电网频率波动的功率谱密度的幅值也越大。图8为图2.C经过时频转换计算得到的秒钟级频率波动时间序列，其对应的累积曲线如图9所示。从图9 A、B两图对比中可以发现，风电渗透率越小，频率波动越平缓，电网稳定性越高，其中A、B两点分别为风电渗透率为20%、10%时电网频率偏差最大值。风电渗透率为20%时，电网频率偏差最大值为0.003 1 pu，而风电渗透率为10%时电网频率偏差最大值为0.001 5 pu，因此风电渗透率降低50%，电网频率波动极值也降低51%左右。若电网频率波动限值为0.001 5 pu（即±0.075 Hz），则风电渗透率为10%恰好满足本调度周期内的稳定要求。

图8　电网频率偏差Fig.8　Grid frequency deviations

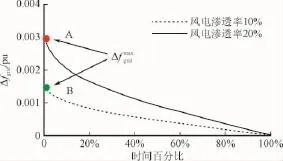
图9　电网频率偏差累积曲线Fig.9　Duration of grid frequency deviations

4.2孤立电网最大风电渗透率评估

霍林河循环经济示范工程尚在建设中，数值天气预测系统尚未建立，为了准确评估孤网系统的最大风电渗透率，取中国气象局提供的风电场规划地区2009年10月1日～2010年9月30日分钟级全年风速数据作为基础数据，对孤网内规划风电场功率波动的功率谱密度进行仿真计算。由于风电功率波动的功率谱密度幅值与平均风速大小密切相关［13］，并且风电场内风机的切入风速为3.5 m/s，额定风速为12 m/s，主要影响风电功率波动的风速区域为5～13 m/s，所以对全年52 560个10 min风电功率波动片段依据输入的风速平均值划分为8组（每个时段以10 min计），即平均风速为5～6、6～7、7～8、8～9、9～10、11～12、12～13 m/s分别对应8组风电功率。每组风电功率波动的平均功率谱密度的计算公式如下：

图10为风电功率波动的平均功率谱密度，该图所示的8段曲线可以全面反映风电场风电功率波动在不同频率的波动大小。对于每种情况，不同平均风速下，风电功率输出功率波动的功率谱密度具有较大的差异。从图10可以看出，该风电场在平均风速为10～11 m/s的组对应的功率谱密度幅值最大，通常称平均风速为10～11 m/s的组为风电功率波动最大组。

图10　风电功率的平均功率谱密度Fig.10　Average power spectral density of wind power

图11为双纵坐标图，左侧纵坐标表示风电渗透率为20%时，不同平均风速组对应的电网频率波动最大值；右侧纵坐标表示在频率约束为0.004 pu时，不同平均风速组对应的最大风电渗透率。由于当风电功率波动功率谱密度在各个频率幅值越大，电网频率波动的功率谱密度的幅度也越大，因此，在考虑风电功率波动对电网频率稳定性影响的时候，只需要考察其输出功率谱密度强度最大的情形，这样可以简化对电网频率波动最大值和风电渗透率极限的计算。表1为不同频率约束下对应的孤立电网最大风电渗透率。孤网频率约束为0.004 pu（即±0.2 Hz），风电渗透率极限为15%。

图11　电网频率偏差及最大风电渗透率Fig.11　Grid frequency deviations and maximum wind power penetration rate

表1　不同频率约束对应的最大风电渗透率Tab.1　Maximum wind power penetration rate that corresponds to different frequency constraint

4.3燃煤燃气机组联合运行提高风电消纳能力

从式（3）可以看出，影响频率波动的因素主要有两个：风电功率波动和电网频率响应能力。图12表示了不同类型的机组频率响应能力。从图12可以看出，相比于火电机组，由于水电机组水力特性的不利影响，调速系统响应速度慢于火电机组，一般不考虑水电机组的一次调频作用。并且内蒙古地区干旱少雨，降水非常少，不适合水电厂的建设和运行。相比较而言，燃气机组具有快速跟踪负荷变化的能力，并且随着中俄输气管道的建设，在蒙东地区建设燃气电站提升系统调频能力成为可能。本文在原有霍林河孤立电网网络结构的基础上，建议增建一定比例的燃气电站，提升孤立电网风电消纳能力。

表2为孤立电网火电机组与燃气机组规划建设容量比例为7∶3时，不同频率约束下电网最大风电渗透率。相比于表1的计算结果，最大风电渗透率在不同频率约束下都有不同程度的提升。孤网频率约束为0.004 pu（即±0.2 Hz），风电渗透率极限为17.4%，风电消纳能力提高了约16%。水电机组、燃气机组的频率响应模型及传递函数见附录B、C。

图12　火电、水电、燃气机组对应的频率响应Fig.12　Frequency respond of different kinds of generators（coal-fired，hydraulic，gas-fired）

表2　不同频率约束对应的最大风电渗透率Tab.2　Maximum wind power penetration rate that corresponds to different frequency constraint

5　结语

本文以霍林河循环经济孤立电网为背景，将风电波动视为平稳随机过程，采用平均功率谱密度提取大量风电波动信息，不借助商业软件，建立了考虑频率约束的孤立电网风电渗透率极限评估模型。利用该模型评估在频率稳定约束下霍林河孤立电网最大风电消纳能力，以期为探索霍林河孤网中合适的频率控制策略提供依据。

研究表明，平均风速在10～11 m/s区间的风电功率波动最为剧烈，对电网频率波动评估影响最大。若频率约束为0.004 pu（即±0.2 Hz），则霍林河孤网的风电渗透率极限为15%左右。机组频率响应能力是影响孤网风电消纳能力的重要因素，本文对不同类型的机组频率响应能力进行了分析，并提出燃煤燃气机组联合运行提高风电消纳能力，为电网后续升级和建设提供了建议。

［1］刘明胜.霍林河循环经济示范项目：风电与电解铝产业结合发展新探索［J］．中国电业（发电板），2014（9）：16-17．LIU Mingsheng.Huolinhe recycling economy demonstration project：new exploration of wind power and electrolytic aluminum industry［J］.China Electric Power，2014（9）：16-17（in Chinese）．

［2］刘玉顺，李志学．发展循环经济建设资源节约型社会是实现可持续发展的必然选择［J］．西部资源，2006（1）：28-29．LIU Yushun，LIZhixue.Developing a recycling economy and resource-saving society is an inevitable choice to achieve sustainable development［J］.Western Resources，2006（1）：28-29（in Chinese）．

［3］孙荣富，张涛，梁吉．电网接纳风电能力的评估及应用［J］．电力系统自动化，2011，35（2）：70-76．SUN Rongfu，ZHANG Tao，LIANG Ji.Evaluation and application of wind power integration capacity in power grid［J］.Automation of Electric Power Systems，2011，35（2）：70-76（in Chinese）．

［4］王军．风电场与电网的匹配-风电场穿透功率极限的确定及其探讨［J］．宁夏电力，2009（1）：53-56．WANG Jun.Confirmation of the best matching between the power grid and wind power field-the penetrating power limit of the wind power generating field［J］.Ningxia Electric Power，2009（1）：53-56（in Chinese）．

［5］罗克宇．风电接入对孤立电网运行的暂态稳定分析研究［J］．农村电气化，2013（S1）：52-54．LUO Keyu.Study of wind power integration on transient stability in an isolated island［J］.Rural Electrification，2013（S1）：52-54（in Chinese）．

［6］张伟．异步风力发电系统并网仿真分析［D］．太原：太原理工大学，2006．

［7］候佑华，齐军，王小海．大规模风电场的建模及其在内蒙古电网安全稳定运行的研究［J］.中国电机工程学报，2010，30（4）：71-78．HOU Youhua，QI Jun，WANG Xiaohai.Modeling of a large-scale wind farm and the studying for its security and stability operation in inner mongolia grid［J］．Proceedings of the CSEE，2010，30（4）：71-78（in Chinese）．

［8］张红光，张粒子，陈树勇，等．大容量风电场接入电网的暂态稳定特性和调度对策研究［J］.中国电机工程学报，2007，27（31）：45-51．ZHANG Hongguang，ZHANG Lizi，CHEN Shuyong，et al.Studies on the transient behavior and dispatching strategy of power system integrated with large scale wind farms［J］.Proceedings of the CSEE，2007，27（31）：45-51（in Chinese）．

［9］胡雪峰，朱涛，高亚静，等．风电高渗透率电网的频率特性及高频切机研究［J］.云南电力技术，2013，41（5）：18-21．HU Xuefeng，ZHU Tao，GAO Yajing，et al.Study on high frequency units shedding and frequency characteristics of power grid with large-scale wind power integration［J］．Yunan Electric Power，2013，41（5）：18-21（in Chinese）．

［10］周专，姚秀萍，常喜强，等．大规模风电并网对孤网频率稳定性影响的研究［J］.中国电力，2014，47（3）：28-32．ZHOU Zhuan，YAO Xiuping，CHANG Xiqiang，et al.Study of impact of bulk wind power integration on isolated grid frequency stability［J］.Electric Power，2014，47（3）：28-32（in Chinese）．

［11］罗克宇，姚保庆，张月文，等．孤立电网的一些稳定问题分析研究［J］.电气应用，2013（S1）：101-106．LUO Keyu，YAO Baoqing，ZHANG Yuewen，et al.Analysis on isolated grid stability［J］.Electrotechnical Applicaztion，2013（S1）：101-106（in Chinese）．

［12］BEVRANI H，GHOSH A，LEDWICH G.Renewable energy sources and frequency regulation：survey and new perspectives［J］.IET Renewable Power Generation，2010（4）：438-457．

［13］LUO C，OOI B T.Frequency deviation of thermal power plants due to wind farms［J］.IEEE Transactions on Energy Conversion，2006（21）：708-716．

［14］JIN L，YUAN-ZHANG S，SORENSEN P，et al.Method for assessing grid frequency deviation due to wind power fluctuation based on“Time-Frequency Transformation”［J］.IEEE Transactions on Sustainable Energy，2012（3）：65-73．

［15］舒征宇，邓长虹，黄文涛，等．含大规模风电的电力系统抽水蓄能最优切泵策略［J］．中国电机工程学报，2013，33（13）：76-84．SHU Zhengyu，DENG Changhong，HUANG Wentao，et al.An opetimal strategy for under-frequency pump shedding of pumped power storage stations based on large-scale wind power integration［J］.Proceedings of the CSEE，2013，33（13）：76-84（in Chinese）．

［16］POTTER C W，NEGNEVITSKY M.Very short-term wind forecasting for Tasmanian power generation［J］.IEEE Transactions on Power System，2006（21）：965-972．

［17］林今，孙元章，S RENSEN P，等．基于频域的风电场功率波动仿真：（一）模型及分析技术［J］.电力系统自动化，2011，35（4）：65-69．LIN Jin，SUN Yuanzhang，S RENSEN P，et al.Simulation of power fluctuation of wind farms based on frequency domain：part one model and analysis technique［J］.Automation of Electric Power Systems，2011，35（4）：65-69（in Chinese）．

［18］林今，孙元章，S RENSEN P，等．基于频域的风电场功率波动仿真：（二）变换算法及简化技术［J］.电力系统自动化，2011，35（5）：71-76．LIN Jin，SUN Yuanzhang，S RENSEN P，et al.Simulation of power fluctuation of wind farms based on frequency domain：part two transformation algorithm and model simplification［J］.Automation of Electric Power Systems，2011，35（5）：71-76（in Chinese）．

［19］PRABHAKUNDUR.Power system stability and control［M］.1994．

［20］KAIMAL J C，WYNGAARD J C，IZUMI Y，et al.Spectral characteristics of surface-layer turbulence［J］.Quarterly Journal of the Royal Meteorological Society，1972（98）：563-598．

［21］SORENSENP，CUTULULISNA，VIGUETAS-RODRIGUEZ

A，et al.Power fluctuations from large wind farms［J］.IEEE

Transaction on Power System，2013（22）：24-33．

附录

A.火电机组频率响应传递函数：

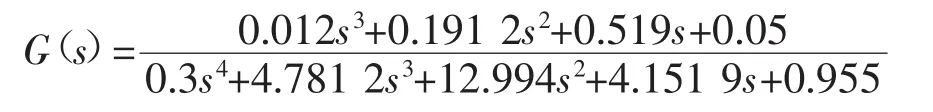
其中模型中模块参数为：

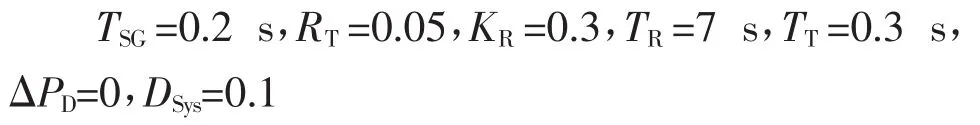
B.水电机组频率响应模型及其传递函数：

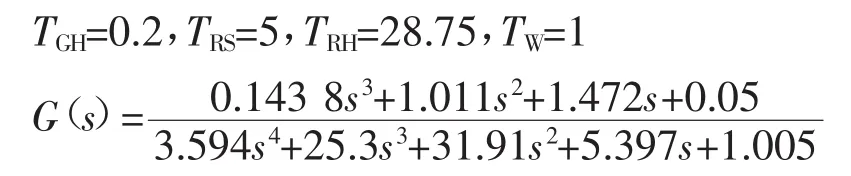
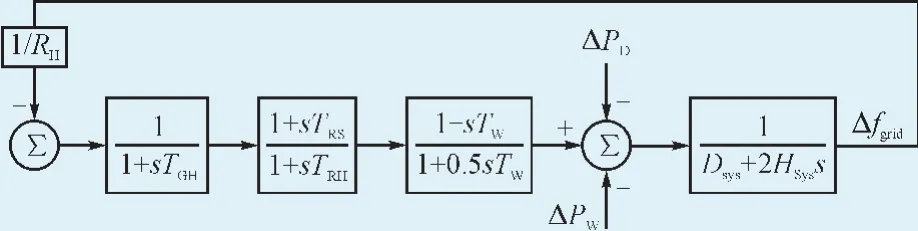
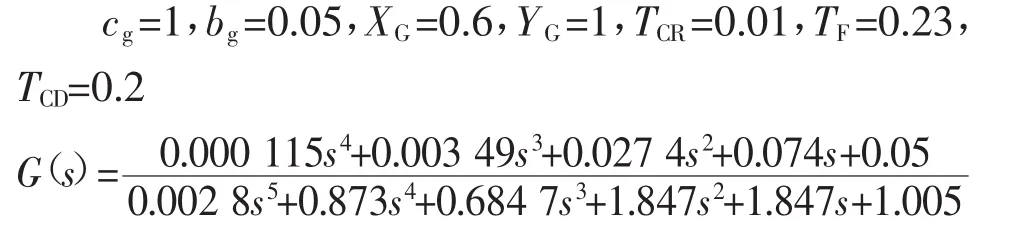
致谢

本文在编写过程中得到了中国科学研究院电工研究所刘怡博士的大力支持和帮助，在此致谢！

（编辑徐花荣）

An Assessment of Wind Power Penetrations Limited with Frequency Constraint in an Isolated System

LIU Jianping1，WU Xichang2，WANG Xubin2，WU Yan1，WANG Zhongwei1，ZHANG Hongli1，LIU Wen1
（1.SPIC Mengdong Energy Group Co.，Ltd.，Tongliao 028011，Inner Mongolia，China；2.School of Electrical&Electronic Engineering，North China Electric Power University，Beijing 102206，China）

High penetration of wind power with the characteristics of randomness and fluctuation affects the grid frequency stability，especially for an isolated power system.Taking the isolated system of Huolinhe recycling economy demonstration project owned by China Power Investment Corporation as a system to be studied，this paper builds an assessment model of maximum wind energy penetration of the studied system limited by grid frequency deviations，which is based on the power spectral density theory considering wind power fluctuation as a stochastic process.Maximum wind power penetrations of the studied system are calculated based on the model.Finally，the paper analyzes frequency response characteristic of different kinds of generators and proposes an approach to increase wind power penetration by increasing the portion of gas power stations.Results can be useful in improving wind power integration level.

wind power penetration；frequency deviation；power spectral density；primary frequency regulation；wind power accommodation

1674-3814（2015）11-0093-08

TM614

A

2015-05-04。

刘建平（1965—），男，高级工程师，研究方向为电力系统发展与规划；

吴锡昌（1990—），男，硕士研究生，研究方向为电力系统稳定与控制。

霍林河循环经济局域电网提升风电消纳能力技术途径研究。

Supported by the Research Project“Study on the Local Power Network in the Huolinhe Green Economic Region to Enhance Its Capability to Accept Wind Power”.