基于时间反转法的相控换能器声场的仿真研究∗

韩珍珍　丁鑫　罗明艳　菅喜岐

（天津医科大学生物医学工程与技术学院天津300070）

基于时间反转法的相控换能器声场的仿真研究∗

韩珍珍丁鑫罗明艳菅喜岐†

（天津医科大学生物医学工程与技术学院天津300070）

相控换能器具有焦距可调的优势。本文以82阵元相控换能器建立的3D数值仿真模型为例，基于时间反转法提取阵元的激励信号，利用时域有限差分（FDTD）法对Westervelt声波非线性传播方程进行声场数值仿真，研究不同阵元分布、焦点偏离声轴的距离、设定焦距大小对形成声场的影响，可调控范围及其消除旁瓣方法。研究结果表明，随机分布相控阵可明显降低声场中的旁瓣；随着偏离声轴距离的增加，主瓣声压幅值逐渐减小，旁瓣与主瓣的最大声强比值r逐渐增大，且沿声轴的可调控范围逐渐减小；随声轴方向上设定焦距的增加，主瓣声压幅值先增大后减小，r值先减小后增大；基于时间反转法的高声压旁瓣消除法可在一定程度上扩大相控阵声场的可调控范围。

高强度聚焦超声，相控换能器，阵元分布，时间反转法，高声压旁瓣消除法

1　引言

高强度聚焦超声肿瘤治疗具有无创、可重复治疗等优势，超声换能器是HIFU肿瘤治疗系统中最关键的部件之一。目前单阵元换能器已应用于乳腺癌、子宫肌瘤、前列腺癌等实体软组织肿瘤的临床治疗［1］，但其焦距固定，肿瘤治疗时需通过机械调整换能器与病患部位的相对位置进行治疗定位。而相控阵换能器可通过相位调控其焦距大小而实现动态聚焦，该研究受到众多研究者的关注。

1996年Goss等［2］提出球面阵元随机分布可改善相控阵声场分布的方法。2005年Lu等［3］采用遗传算法对256矩形阵元相控阵中每个阵元的幅值和相位进行调控以降低声场中旁瓣。2009年Hand等［4］通过仿真和离体实验对254阵元随机相控阵单焦点和多焦点的动态调控范围进行了测定。2012年Ji等［5］设计了用于治疗深部肿瘤的90阵元大开口半随机分布的球面相控阵。

本文根据周期、同心环和随机分布设计的82阵元相控阵换能器建立3D数值仿真模型，并基于时间反转法提取相位控制信号，利用Westervelt声波非线性传播方程进行时域有限差分数值仿真研究，以旁瓣与主瓣的最大声强比值r≤0.25为判断标准［6］讨论不同聚焦位置时的声场变化规律、焦点可调控范围。并提出扩大焦域可调控范围的高声压旁瓣消除法。

2　方法与模型

2.1声波传播方程式

Westervelt声波传播方程式［7-8］为

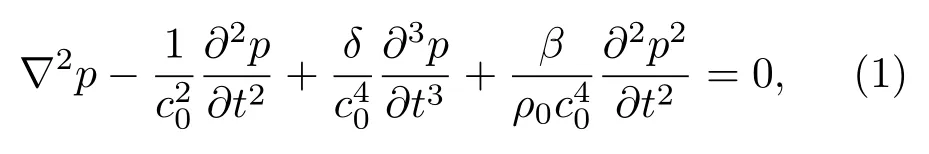
（1）式中：∇为拉普拉斯算子；p为声压；c0和ρ0分别为介质的声速和密度；β=1+B/（2A）为声波非线性系数，B/A为流体介质的非线性系数；为声波扩散系数；α为吸收系数；ω=2πf为角频率，f为频率。

采用时域有限差分法［9-10］对（1）式进行中心差分，差分方程式为

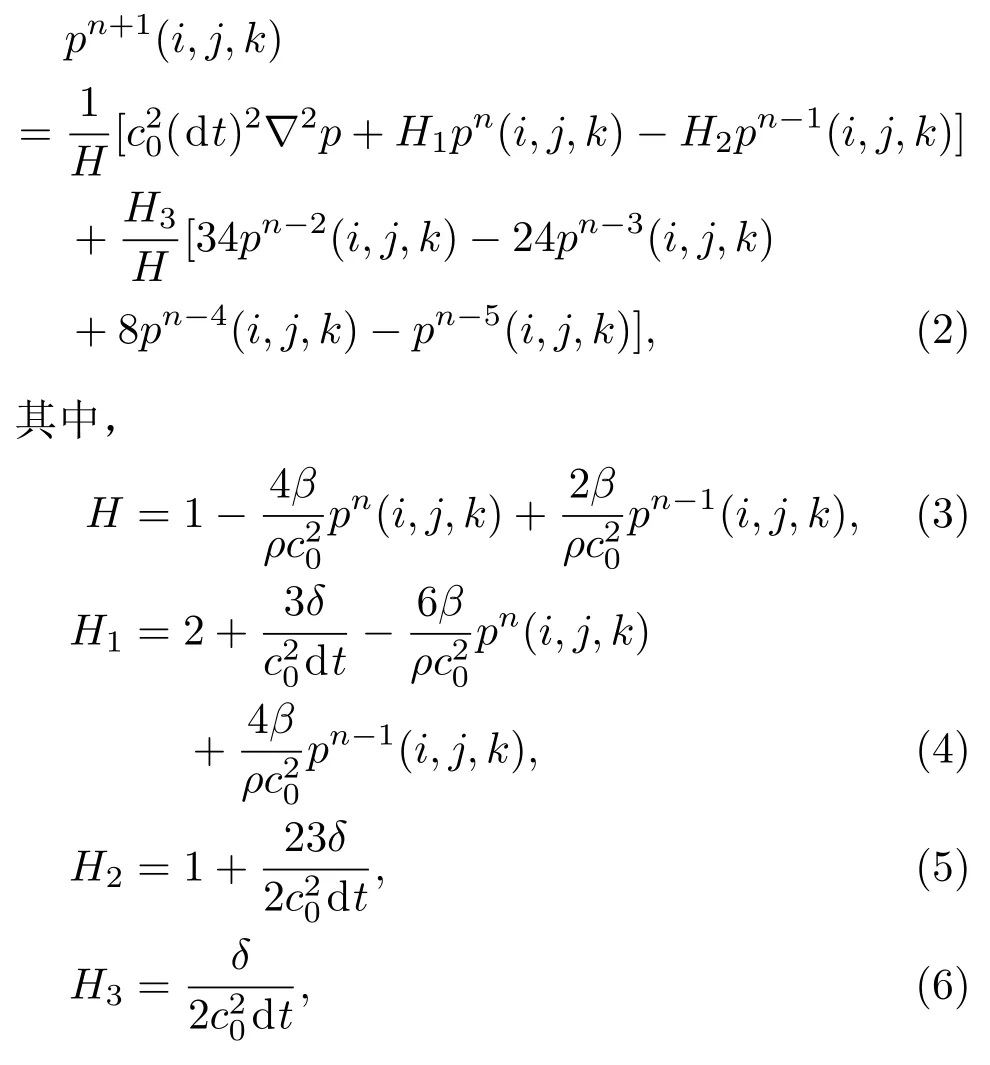
i、j、k分别为直角坐标系下x、y、z三个坐标轴方向的坐标，dx、dy、dz分别表示x、y、z三个坐标轴方向的空间步长，dt为时间步长，n为计算时刻。

2.2阵元相位获取法

基于时间反转法［11-12］在目标焦点S处设置正弦函数点声源S0（t），数值仿真得到传到相控阵编号为m阵元中心点的声压信号S0m（t），将该信号按时间序列进行反转后，得到对应阵元m的信号S0m（T-t）。利用最小二乘函数拟合法计算一段时间内S0m（T-t）的相对初始相位延迟Δtm，然后以同一输入声强对正弦信号幅值进行调制，阵元m的激励信号为

如果在（7）式激励信号触发相控阵换能器阵元形成的声场中出现声压幅值较高的旁瓣，确定其位置R，采用同样的方法计算聚焦在R处相控换能器阵元m的激励信号。对分别聚焦在S和R处的激励信号线性叠加，调控聚焦在R处的输入声强使在R处聚焦时稳态声压的最大幅值与聚焦在S处时R位置的稳态声压幅值相等，且使聚焦在R处的相位相对聚焦在S处的相位180°延迟，从而达到降低R处高声压旁瓣幅值［13］的目的。

2.3数值仿真模型和参数

图1为开口直径100 mm、曲率半径80 mm、曲率半径与开口直径之比F值为0.8的82阵元相控阵换能器和水体组成的数值仿真模型。其中数值仿真区域为边长为100 mm的立方体，声轴为x轴。图2（a）、2（b）、2（c）分别为阵元按照周期、同心环和随机分布构成的82阵元相控换能器，其中阵元直径均为8 mm、阵元填充率为52.48%，周期分布相邻阵元中心间距均为9.5 mm；同心环分布中阵元中心点所在环半径由内到外依次为9 mm、18 mm、27 mm、36 mm、45 mm，对应的阵元数目分别为6、11、16、21、27；随机分布通过Matlab随机数生成器获得，四个象限内阵元数目依次为21、21、20、20，在相邻阵元中心间距不小于8.7 mm的条件下，依次选定各象限中其余阵元的中心位置。

水体的仿真参数为ρ0=998 kg/m3，c0= 1486 m/s，β=3.5，α=0.02 Np/（m·MHz）［14］。换能器激励函数为频率为0.7 MHz的连续正弦波，边界采用Mur一阶边界吸收条件。空间步长dx=dy=dz=0.25 mm，时间步长dt=10 ns。

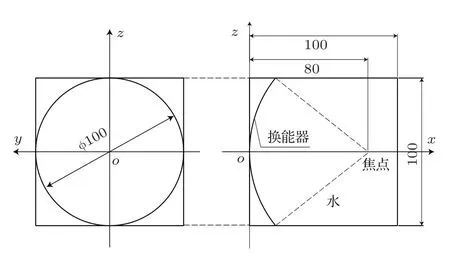
图1　数值仿真模型图（单位：mm）Fig.1 Numerical simulation model（Unit：mm）

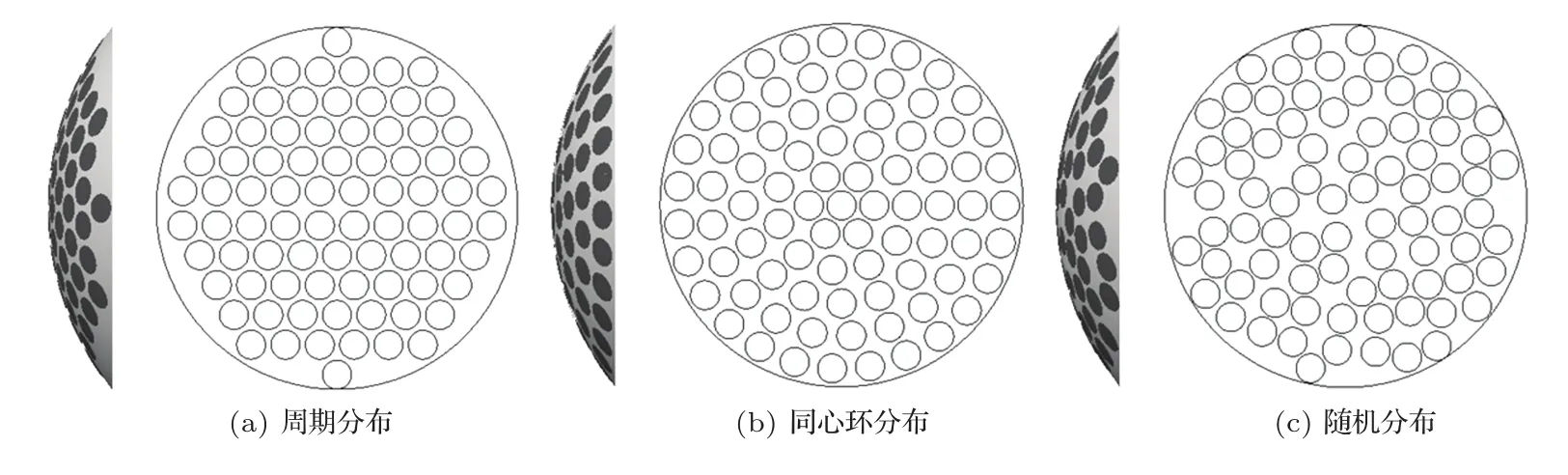
图2　阵列结构图Fig.2 Array structure diagram

3　结果

3.1不同阵元分布形成的声场

当输入声强为1 W/cm2，设定焦点为几何焦点（80，0，0）mm时，周期分布、同心环分布和随机分布相控阵在x轴上形成的声压变化曲线如图3所示，其中黑色虚线为周期分布、灰色实线为同心环分布、黑色实线为随机分布。由图3可知，三种分布阵列形成的最大声压（主瓣）幅值分别为4.800 MPa、4.716 MPa、4.777 MPa，实际焦距分别为78.25 mm、77.75 mm、77.75 mm，均小于设定的80 mm几何焦距，周期分布和同心环分布阵列在主瓣左侧旁瓣多且幅值较大，随机分布相控阵仅在靠近主瓣左侧有一个较小旁瓣。图4为三种不同分布阵列在几何焦点聚焦时实际形成的焦平面声场分布图，由图4可知周期分布阵列焦域周围有六个明显的旁瓣，同心环分布阵列焦域周围有两层旁瓣，随机分布阵列仅在焦域附近有分布无规则的较小旁瓣。对上述三种不同分布相控阵在几何焦点聚焦时实际形成的三维声场进行分析，周期、同心环、随机分布阵列中旁瓣与主瓣的最大声强比值分别为0.1400、0.2358、0.1247，随机分布阵列的比值最低。

图3　不同阵元分布相控阵在x轴上形成的声压变化曲线图Fig.3The acoustic pressure curve along the xaxis of phased arrays with different element distribution

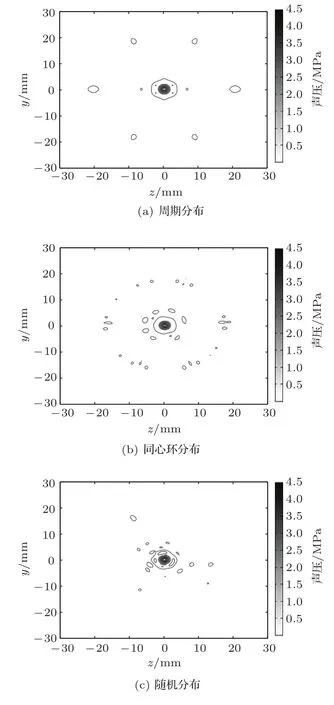
图4　在几何焦点聚焦时的焦平面声场分布图Fig.4 The acoustic field distribution of the focal plane when focusing at geometric focus

3.2偏离声轴聚焦的声场分布

当输入声强为1 W/cm2，设定焦点位置为x轴80 mm、z轴0 mm、沿y轴正方向以1 mm为步长偏离x轴聚焦时，形成焦点位置处最大声压的变化曲线如图5（a）所示，其中灰色实线为周期分布、黑色虚线为同心环分布、黑色实线为随机分布，由图5（a）可知随着偏离x轴距离的增加三种分布相控阵最大声压值均逐渐减小，且变化趋势基本一致。图5（b）为与图5（a）相应的旁瓣与主瓣最大声强比值r的变化曲线，由图5（b）可知随着偏离x轴距离的增加该比值均逐渐增大，同心环分布和周期分布阵列的r值均明显高于随机分布阵列。由图3∼5可知，与周期和同心环分布阵列相比，随机分布阵列可以明显降低声场中的旁瓣，为此选用随机分布相控换能器进行声场讨论分析。

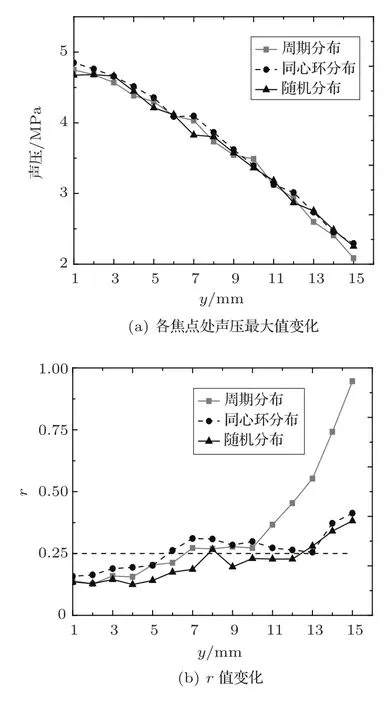
图5　三种不同分布阵列沿y轴聚焦时的声场变化Fig.5The acoustic variation as a function of focal spot location along the y-axis for three phased arrays with different element distribution

以图2（c）随机分布相控阵为例，当设定焦点为（80，5，0）、（80，10，0）、（80，15，0）时实际形成的焦平面声场分布如图6所示，由图6可知随着偏离x轴距离的增加，分布在焦域周围的旁瓣逐渐移至焦域下方，并且旁瓣数量逐渐增多、幅值逐渐增大。由图5（b）可知，随机分布相控阵在偏离x轴8 mm聚焦形成的声场中r=0.2664，超过了0.25，其xy平面声场分布如图7（a）所示，对图7（a）所示的靠近焦域左下方的旁瓣进行高声压旁瓣消除后，xy平面的声场分布如图7（b）所示，使其旁瓣幅值明显降低，且r=0.1534。同时高声压旁瓣消除后，二次声压旁瓣幅值由1.963 MPa下降为1.192 MPa，下降率为39.28%，而主瓣声压幅值由3.803 MPa变为3.403 MPa，下降率仅为10.52%。当对随机分布相控阵进行高声压旁瓣消除后，可使其实现最大偏离x轴12 mm的调控聚焦。

图6　随机分布相控阵在不同焦点位置聚焦时归一化后焦平面声场分布图Fig.6 The acoustic field distribution of the focal plane for the quasi-random phased array with different focal location

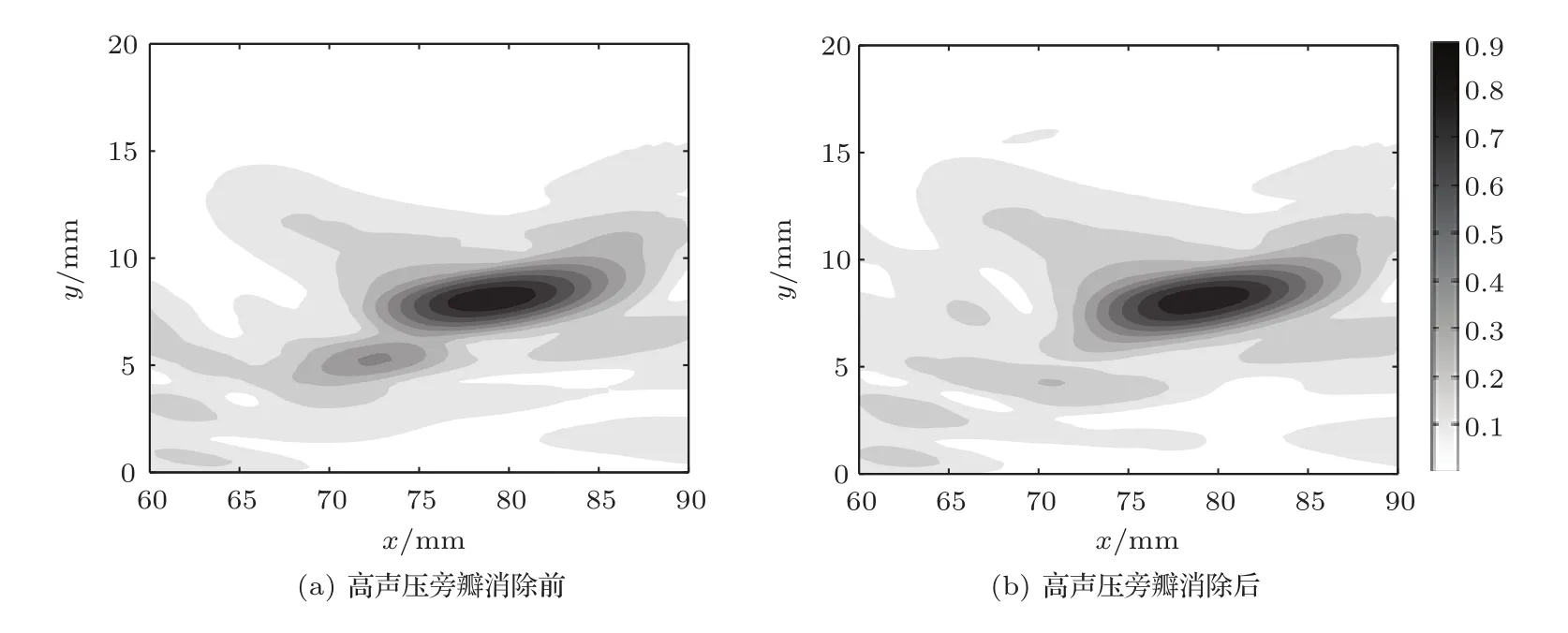
图7　随机分布相控阵在（80，8，0）聚焦时归一化后xy平面声场分布图Fig.7The acoustic field distribution in the xy plane for the quasi-random phased array when focusing at（80，8，0）

3.3随机分布相控阵沿声轴聚焦

当输入声强为1 W/cm2，设定目标焦点在z=0平面，y方向上分别沿x轴、偏离x轴5 mm、10 mm、12 mm，沿x轴方向的焦距范围均在55∼90 mm调控的条件下，形成声场中最大声压值随设定焦点位置的变化曲线如图8（a）所示，其中灰色虚线为沿x轴、灰色实线为偏离x轴5 mm、黑色虚线为偏离x轴10 mm、黑色实线为偏离x轴12 mm，由图8（a）可知在y轴方向偏离x轴距离相同的条件下，随x轴方向上设定焦距的增加，形成的最大声压值先增大后减小，且偏离x轴的距离不同形成最大声压的位置也不同，分别为x=70 mm、75 mm、75 mm、80 mm。在x轴方向上调控位置相同时，随着y轴方向上偏离x轴距离的增加，形成的最大声压值逐渐降低。图8（b）为与图8（a）相同条件下随设定焦点位置的r值变化曲线，由图8（b）可知随着y方向上偏离x轴距离的增加，r值逐渐增大，随着x轴方向上设定焦距值的增加r值先减小后增大，形成最小r值的位置有所不同，分别为x=65 mm、65 mm、75 mm、80 mm。在r≤0.25的判断条件下，x轴上的可调控范围为55∼90 mm，y方向上偏离x轴5 mm、10 mm沿x轴方向聚焦的可调控范围分别为55∼90 mm、60∼80 mm，y方向上偏离x轴12 mm仅有x=80 mm和x=90 mm两点。随着y方向上偏离x轴距离的增加，沿x轴方向的声场可调控范围逐渐减小。同时由图8（b）可知，在偏离x轴10 mm、12 mm聚焦时，分别有x=55、60、85、90 mm和x=55、60、65、70、75、85 mm位置处r值均大于0.25，且在x=85 mm调控聚焦时均有一波峰值，分别进行高声压旁瓣消除后的r值变化曲线如图8（c）所示，由8（c）可知偏离x轴10 mm、12 mm分别对应x轴方向可调控范围分别不小于60∼90 mm、80∼90 mm。焦点在（80，12，0）位置调控聚焦时形成的xy和yz平面声场分布如图9所示。由图9可知，在焦域附近没有较大的声压旁瓣出现。

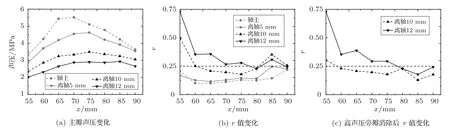
图8　随机分布相控阵y方向上偏离x轴不同距离时沿x轴以5 mm步长调控聚焦时的声场变化规律Fig.8 The acoustic variation as a function of focal spot location along the x-axis and off y-axis different distance from x-axis for the quasi-random phased array

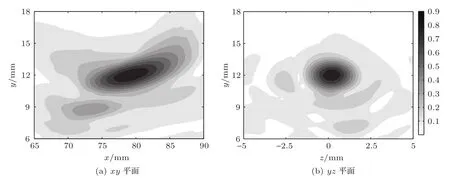
图9　随机分布相控阵在（80，12，0）位置聚焦时的归一化声场分布图Fig.9 The acoustic field distribution when focusing at（80，12，0）for the quasi-random phased array

4　讨论与结论

本文设计了周期、同心环、随机三种不同分布的相控阵，基于时间反转法进行相位调控，分析比较其声场分布特点和变化规律，并结合基于时间反转法的高声压旁瓣消除法增大随机分布相控阵声场的可调控范围。结论如下：

（1）与周期和同心环分布阵列相比，随机分布阵列可明显降低声场中的旁瓣，改善声场分布，这与Gavrilov等［6］的研究结果一致。

（2）随声轴方向上设定焦点和换能器间距离的增加，主瓣声压幅值先增大后减小，旁瓣与主瓣的最大声强比值先减小后增大。同时随着偏离声轴距离的增加，主瓣声压幅值逐渐减小，旁瓣与主瓣的最大声强比值逐渐增大，且沿声轴的声场可调控范围逐渐减小，该结果与Raju等［15］的研究结果相近。

（3）基于时间反转法的高声压旁瓣消除法可在一定程度上增大相控阵声场的可调控范围。

上述结论是在高强度聚焦声场的仿真研究中得出的，对于声压幅值较小的超声波而言，一般呈线性传播，但对HIFU治疗肿瘤而言，其焦点声压一般较高，因此需要考虑超声传播的非线性特性。

在基于时间反转法获取阵元的激励信号时，声波的不同传递过程中具有一定非线性差异，2010年Pinton等［16］的研究结果表明对相控阵的相位差计算时其影响可忽略不计。为此本文在获取阵元激励信号时未考虑其非线性的影响。

本文仅以水体内相控换能器形成的声压场进行分析讨论。对于非均质人体组织的仿真研究中，可利用2003年Aubry等［17］提出的基于CT数据获取组织声学参数的方法，建立结合临床实际的数值仿真模型，研究其形成的声场特性。基于人体CT数据的数值仿真正在进行中。

［1］KENNEDY J E.High-intensity focused ultrasound in the treatment of solid tumours［J］.Nature Reviews Cancer，2005，5（4）：321-327.

［2］GOSS S A，FRIZZELL L A，KOUZMANOFF J T，et al.Sparse random ultrasound phased array for focal surgery［J］.IEEE Trans.Ultrason.Ferroelectr.Freq. Control，1996，43（6）：1111-1121.

［3］LU Mingzhu，WAN Mingxi，XU Feng，et al.Focused beam control for ultrasound surgery with spherical-section phased array：sound field calculation and genetic optimization algorithm［J］.IEEE Trans.Ultrason.Ferroelectr. Freq.Control，2005，52（8）：1270-1290.

［4］HAND J W，SHAW A，SADHOO N，et al.A random phased array device for delivery of high intensity focused ultrasound［J］.Phys.Med.Biol.，2009，54（19）：5675-5693.

［5］JI Xiang，SHEN Guofeng，BAI Jingfeng，et al.The characterization of an ultrasound spherical phased array for the ablation of deep-seated tissue［J］.Appl.Acoust.，2012，73（5）：529-534.

［6］GAVRILOV L R，HAND J W.A theoretical assessment of the relative performance of spherical phased arrays for ultrasound surgery［J］.IEEE Trans.Ultrason.Ferroelectr. Freq.Control，2000，47（1）：125-139.

［7］HAMILTON M F，BLOCKSTOCK D T.Nonlinear Acoustics［M］.Boston：Academic Press，1998.

［8］BAILEY M，KHOKHLOVA V，SAPOZHNIKOV O，et al. Physical mechanism of the therapeutic effect of ultrasound（A review）［J］.Acoustic Physics，2003，49（4）：369-388.

［9］YEE K S.Numerical solution of initial boundary value problems involving Maxwell's equations［J］.IEEE Trans. Antennas Propag，1966，14（3）：302-307.

［10］RADZEVICIUS S J，CHEN C C，ETERS J L，et al.Nearfield dipole radiation dynamics through FDTD modeling［J］.Journal of Applied Geophysics，2003，52（2）：75-91.

［11］THOMAS J L，FINK M A.Ultrasonic beam focusing through tissue inhomogeneities with a time reversal mirror：application to transskull therapy［J］.IEEE Trans. Ultrason.Ferroelectr.Freq.Control，1996，43（6）：1122-1129.

［12］王意喆，张千，周文征，等.HIFU经颅治疗中降低颅骨声压的仿真研究［J］.计算机仿真，2014，31（5）：209-213. WANG Yizhe，ZHANG Qian，ZHOU Wenzheng，et al. Simulation study on reducing acoustic pressure on skull during HIFU transcranial therapy［J］.Computer Simulation，2014，31（5）：209-213.

［13］LEDUC N，OKITA K，SUGIYAMA K，et al.Focus control in HIFU therapy assisted by time-reversal simulation with an iterative procedure for hot spot elimination［J］. Journal of Biomechanical Science and Engineering，2012，7（1）：43-56.

［14］GINTERS.Numericalsimulationofultrasoundthermotherapy combining nonlinear wave propagation with broadband soft-tissue absorption［J］.Ultrasonics，2000，37（10）：693-696.

［15］RAJU B I，HALL C S，SEIP R.Ultrasound therapy transducers with space-filling non-periodic arrays［J］.IEEE Trans.Ultrason.Ferroelectr.Freq.Control，2011，58（5）：944-954.

［16］PINTON G，AUBRY J F，FINK M，et al.Effects of nonlinear ultrasound propagation on high intensity brain therapy［J］.Medical Physics，2011，38（3）：1207-1216.

［17］AUBRY J F，TANTER M，PERNOT M，et al.Experimental demonstration of noninvasive transskull adaptive focusing based on prior computed tomography scans［J］. The Journal of the Acoustical Society of America，2003，113（1）：84-93.

The simulation study of acoustic pressure field about HIFU phased array transducer based on time reversal method

HAN ZhenzhenDING XinLUO MingyanJIAN Xiqi
（Department of Biomedical Engineering and Technology，Tianjin Medical University，Tianjin 300070，China）

Phased array transducer has the advantage of adjustable focal length.In this paper，the incentive signal of each element is abstracted by time reversal method and the acoustic pressure numerical simulation is undergone through finite difference time domain（FDTD）of Westervelt acoustic nonlinear transmission formula based on the 3D numerical simulation model of 82-element phased array transducer.The effect of different element distribution，the distance off the acoustic axis and the setting focal length on the forming acoustic pressure field is discussed.The adjustable range of acoustic pressure field and the method which eliminate sidelobe is also analyzed.The results show that the phased array transducer with quasi-random distribution can suppress the sidelobe significantly.As the distance off the acoustic axis increasing，the acoustic pressure amplitude of the main lobe decreases，the acoustic intensity ratio between the maximum sidelobe and the main lobe（r value）increases，and the adjustable range along the acoustic axis decreases.The acoustic pressure amplitude of the main lobe increases firstly and then decreases，while r value decreases firstly and then increases with the increase of setting focal length along the acoustic axis.To some extent，the acoustic adjustable range can be extended by the high acoustic pressure sidelobe elimination method based on time reversal method.

High-intensity focused ultrasound，Phased array transducer，Element distribution，Time reversal method，High acoustic pressure sidelobe elimination method

R318.5

A

1000-310X（2015）04-0344-07

10.11684/j.issn.1000-310X.2015.04.009

2014-10-29收稿；2015-02-16定稿

∗国家自然科学基金项目（81272495）

韩珍珍（1989-），女，山东潍坊人，硕士研究生，研究方向：超声医学。†

E-mail：jianxiqi@tmu.edu.cn