基于纯方位的浅海距离特征量解算分析∗
2015-10-26赵建昕过武宏笪良龙徐国军
赵建昕 过武宏 笪良龙 徐国军
(海军潜艇学院 青岛 266071)
基于纯方位的浅海距离特征量解算分析∗
赵建昕†过武宏笪良龙徐国军
(海军潜艇学院青岛266071)
目标辐射噪声的LOFAR图中的干涉条纹包含了目标的运动参数和环境信息。当LOFAR图中的干涉条纹模糊或缺失时,其中的目标距离信息将无法提取。对于匀速直线运动的声源目标,仅利用方位信息,通过构造距离特征量和目标方位的关系模型,给出了一种估计浅海距离特征量的补充方法。浅海数值仿真和实验验证表明了该方法的可行性和有效性。
纯方位,距离特征量,速度距离比
1 引言
海洋波导中存在着低频声场时空干涉现象,这种现象可通过舰艇辐射噪声的干涉谱图(LOFAR)来描述,其中包含的信息有助于对目标进行运动状态估计和分类识别,如文献[1—7],其基本的做法是估计干涉条纹的斜率,进而利用波导不变量、声源频率和距离的关系来估计目标运动参数。不同于上述文献的做法,利用波导不变量,文献[8—9]提出了目标距离特征量的概念,并用于估计目标运动参数,为了获取精度较高的距离特征量估计值,文献[10—11]分别研究了距离特征量的提取方法。
不难看出,上述文献的研究基础都是假设LOFAR谱图中有较为清晰的干涉条纹,并能提取较高精度的距离特征量估计值。但是,由于海洋环境的复杂性,实际水下目标的LOFAR谱图中会叠加有大量的噪声,干涉条纹往往不清晰,严重时甚至淹没在噪声中。没有干涉条纹,这必然影响距离特征量值提取及提取的精度,从而影响目标运动参数的估计。
为此,本文针对干涉条纹不清晰或没有干涉条纹的情形,利用目标方位信息研究目标距离特征量的提取问题,给出了一种估计方法。以下总假定目标和观测站作匀速直线运动,观测站不需要做机动动作,这是有利于观测站隐蔽的。
2 距离特征量
由文献[8—9]知,距离特征量是指在目标声源与接收器相对运动过程中,tk时刻目标声源与接收器之间的距离与t0时刻距离的比值,它描述的是目标瞬时距离与初距的比值,用ℜt表示。
3 参数估计
假定目标和观测站均作匀速直线运动,观测站初始位于坐标原点,只考虑在其运动平面的两维情形,图1给出观测站和目标的二维几何态势。图2给出两者的相对运动态势图。
D0:目标初始距离(m);Di:ti时刻目标瞬时距离(m);Fk:tk时刻观测站测得的目标方位,k=0,1,2,···;Cm:目标航向,以y轴方向为起点,右旋取值0∼2π;Cw:观测站航向,以y轴方向为起点,右旋取值0∼2π;Vmx,Vmy:分别表示目标匀速直线运动的速度(m/s)的x轴、y轴分量;Vwx,Vwy:分别表示观测站运动时的速度(m/s)的x轴、y轴分量;Vx,Vy:分别表示目标相对于观测站速度的x轴、y轴分量;V:目标相对于观测站速度;X0:为初始时刻t0的目标舷角;
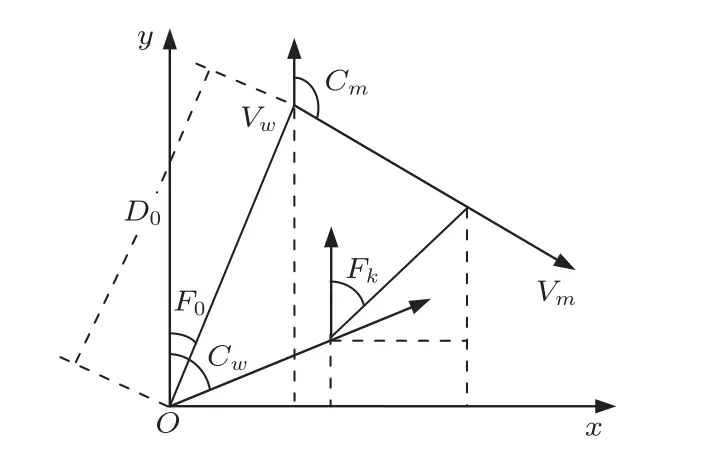
图1 观测站和目标二维几何态势Fig.1The geometric situation between target and observer

图2 观测站和目标相对态势Fig.2 The relative situation between target and observer
3.1速度距离比和初始时刻目标舷角的估计
当输入目标方位Fk时,目标方位与D0,Vx,Vy的关系或测量模型为


同上分析不难得到,矩阵BTB是可逆矩阵,则上述等式中的参数cosX0,sinX0可以利用最小二乘法估计得到

结合参数V/D0的估计,可得到初始时刻目标舷角的余弦值。
3.2距离特征量的估计及误差分析
记Di为ti时刻的目标距离,由图2和相对运动规律,结合余弦定理知,

将3.1中的速度距离比和目标舷角余弦估计值代入(8)式可得到距离特征量的估计

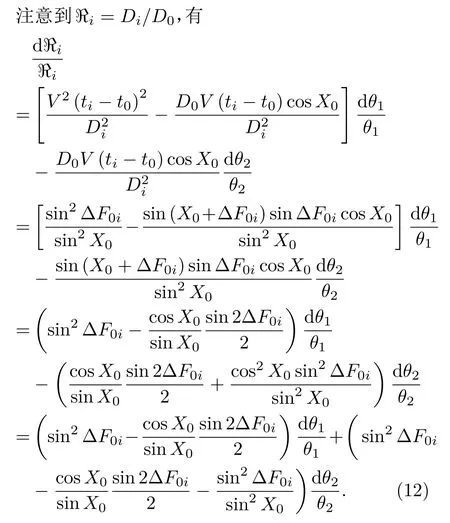

4 模拟仿真与实验验证
下面通过数值模拟和实验数据验证,检验本文方法的有效性和可行性。
假设观测站和目标分别沿自身航向作匀速直线运动,观测站不做机动运动。考虑两类态势,一是目标接近;二是目标远离。
以时间总长600 s为例,抽样时间2 s,系统仿真50 s后,才开始对目标要素估计,其它的参数设定见表1。
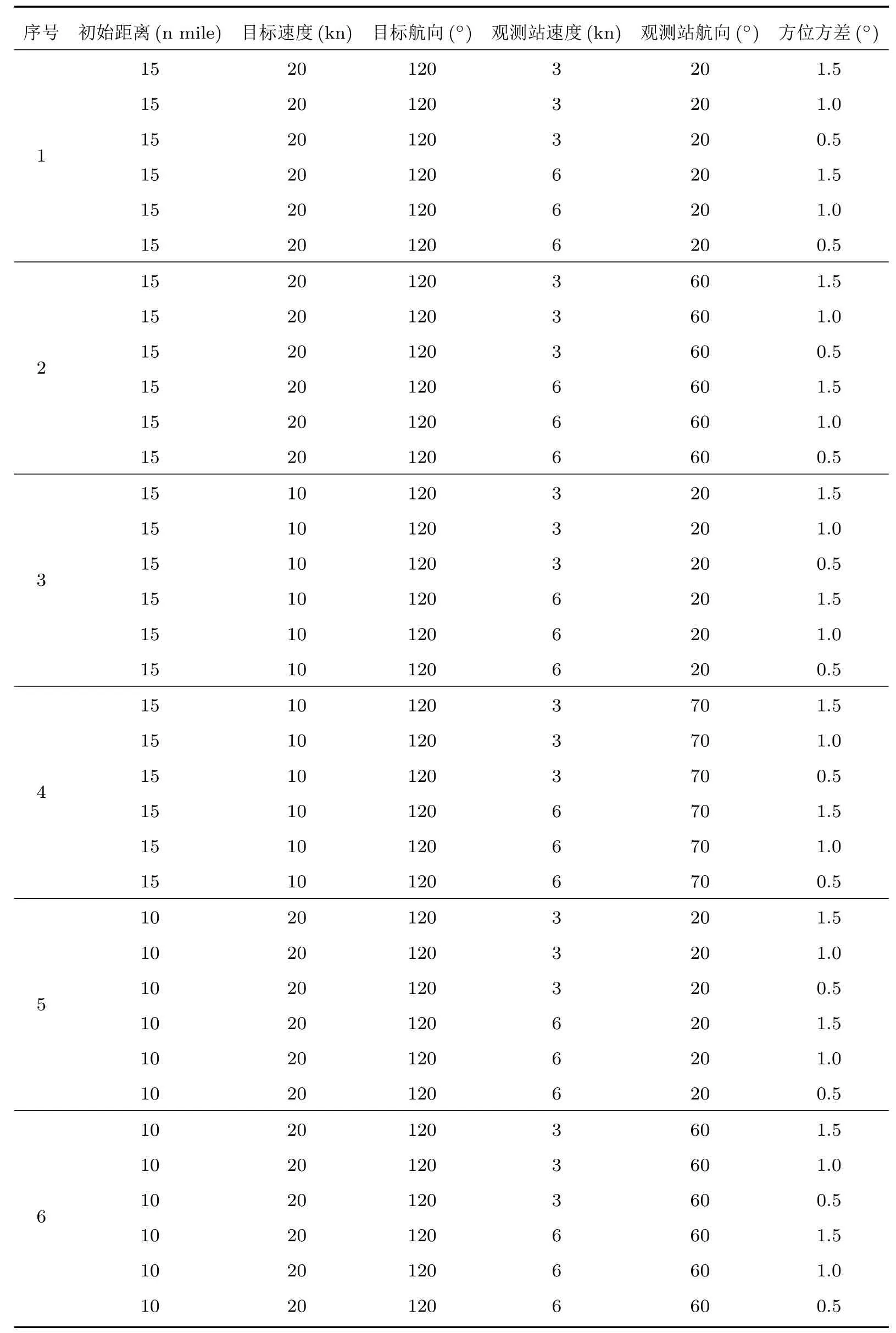
表1 观测站和目标数值模拟要素值Table 1Numerical simulation elements of target and observer
图3对应的实验序号1,给出了初距15海里目标接近态势,两种不同的观测站速度,3种不同的方位误差的模拟结果。

图3 初距15海里,目标接近态势,观测站两种不同速度,上述三参数的估计结果Fig.3 The estimates of three parameters with observer at different speeds,target closing situation and 15 nautical miles at original time
图4对应的实验序号2,给出了初距15海里目标远离态势,两种不同的观测站速度,3种不同的方位误差的模拟结果。
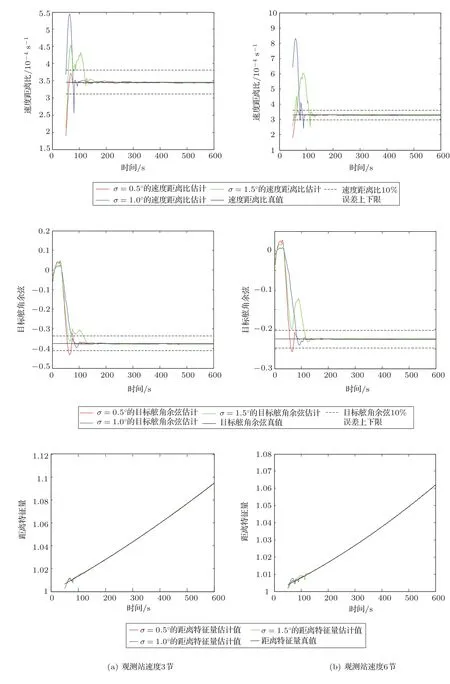
图4 初距15海里,目标远离态势,观测站两种不同速度,上述三参数的估计结果Fig.4The estimates of three parameters with observer at different speeds,target moving away and 15 nautical miles at original time
图5对应的实验序号3,给出了目标初速10节接近态势,两种不同的观测站速度,3种不同的方位误差的模拟结果。
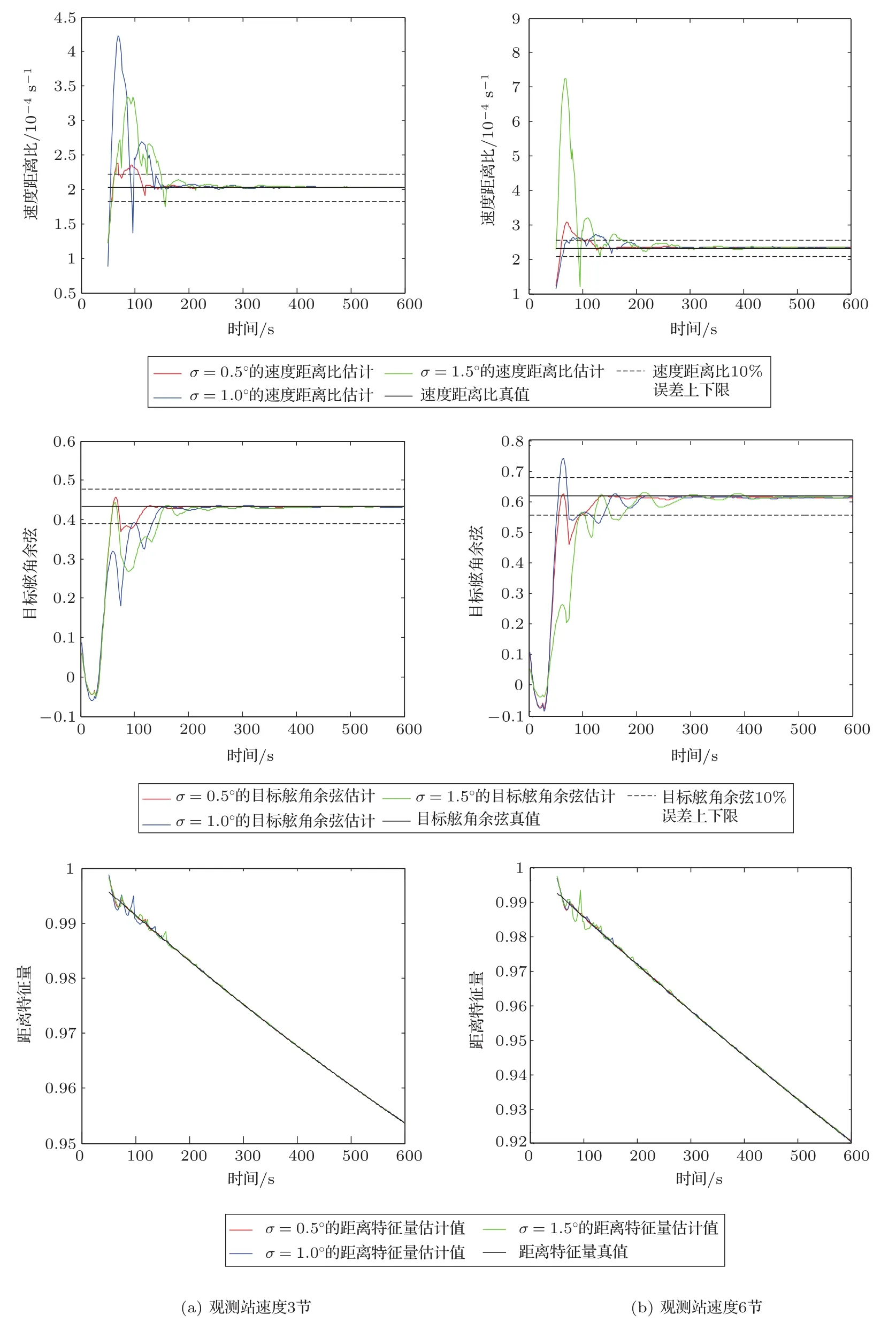
图5 目标初速10节,目标接近态势,观测站两种不同速度,上述三参数的估计结果Fig.5 The estimates of three parameters with observer at different speeds,target closing situation and speed of 10 knots
图6对应的实验序号4,给出了目标初速10节远离态势,两种不同的观测站速度,3种不同的方位误差的模拟结果。
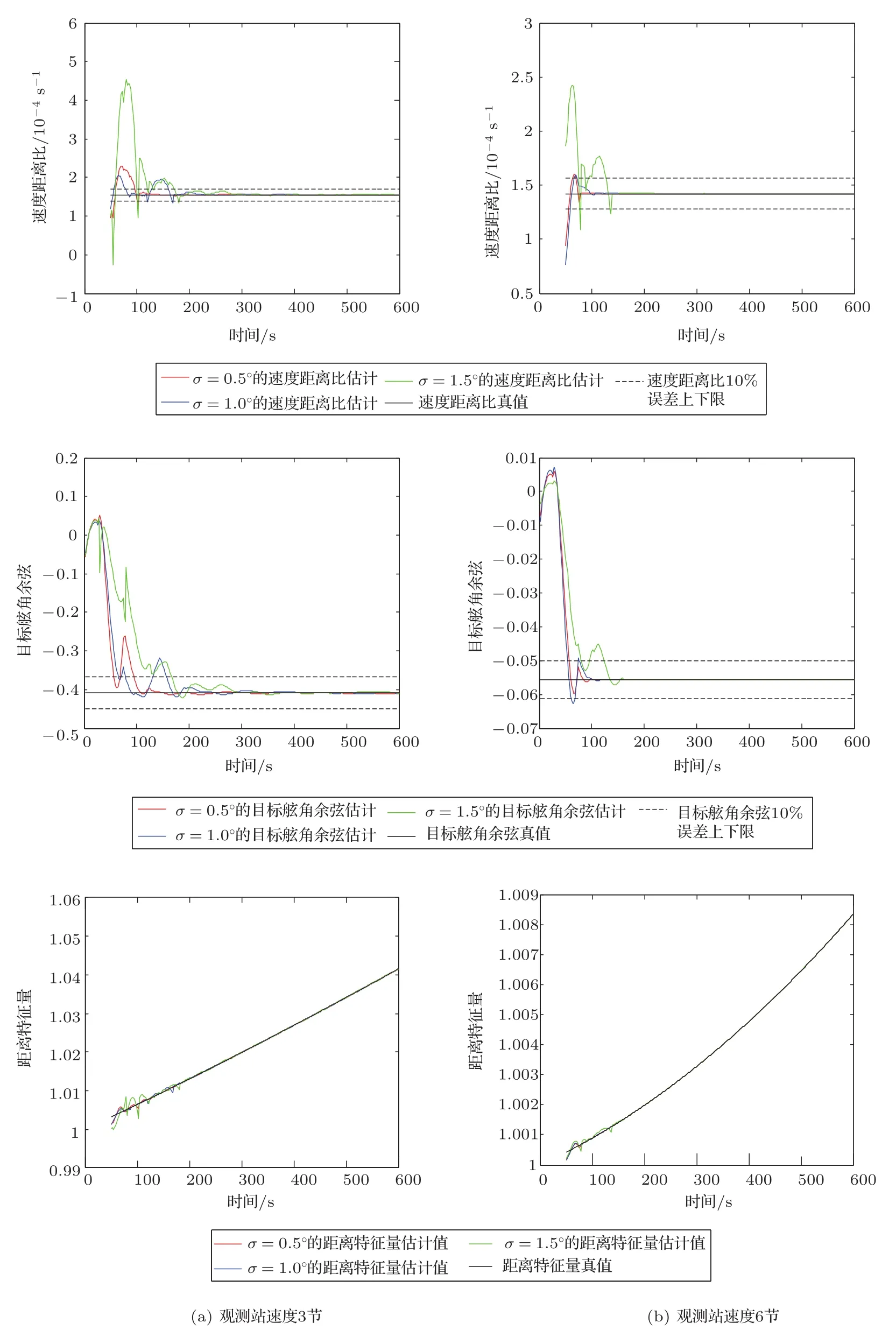
图6 目标初速10节,目标远离态势,观测站两种不同速度,上述三参数的估计结果Fig.6The estimates of three parameters with observer at different speeds,target moving away and speed of 10 knots
图7对应的实验序号5,给出了初距10海里目标接近态势,两种不同的观测站速度,3种不同的方位误差的模拟结果。

图7 初距10海里,目标接近态势,观测站两种不同速度,上述三参数的估计结果Fig.7 The estimates of three parameters with observer at different speeds,target closing situation and 10 nautical miles at original time
图8对应的实验序号6,给出了初距10海里目标远离态势,两种不同的观测站速度,3种不同的方位误差的模拟结果。
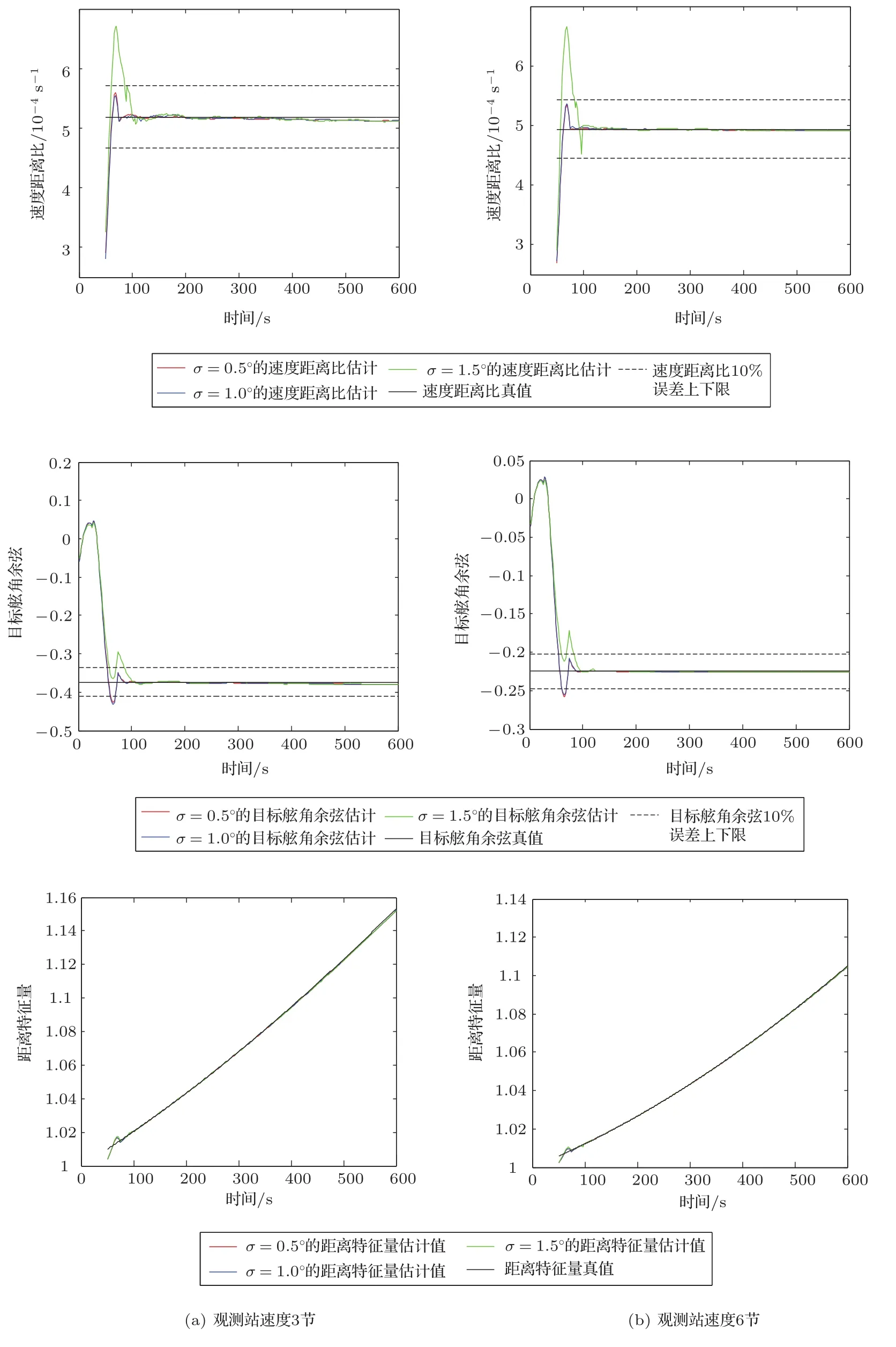
图8 初距10海里,目标远离态势,观测站两种不同速度,上述三参数的估计结果Fig.8The estimates of three parameters with observer at different speeds,target moving away and 10 nautical miles at original time
从上述选择的实验模拟结果不难看出:
(1)目标远离或接近态势,速度距离比、目标舷角和距离特征量大约都在200 s内收敛,这说明了方法的正确性。
(2)目标远离或接近态势,三参数估计的收敛时间随着方位误差的增加呈增长趋势。
(3)参数估计的收敛时间与相对运动态势有关,如速度20节的目标与速度10节的目标相比,前者三参数估计的收敛时间要少,方位的变化率大是重要的原因。
为了进一步验证文中方法在实际环境中的性能,选取了两次实验数据,观测站和目标的初始时刻各要素值见表2,图9给出了各要素随时间变化实际值。
图10—图11给出了实际中两种态势下的参数估计随时间变化情况。由于海上实验时,观测站和目标的要素不能保持绝对的匀速和直航,因此,速度距离比、目标舷角和距离特征量三参数的估计收敛的时间都要比数值模拟得到三参数的估计收敛的时间长,但从这两个实际数据看,在300 s内,距离特征量均收敛。

表2 观测站和目标初始时刻的各要素实际值Table 2 Real elements of target and observer at original time

图9 观测站和目标的各要素实际值Fig.9 Real elements of target and observer
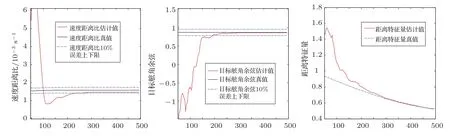
图10 表2序号1的计算结果Fig.10 Calculation results of No.1 in Table 2
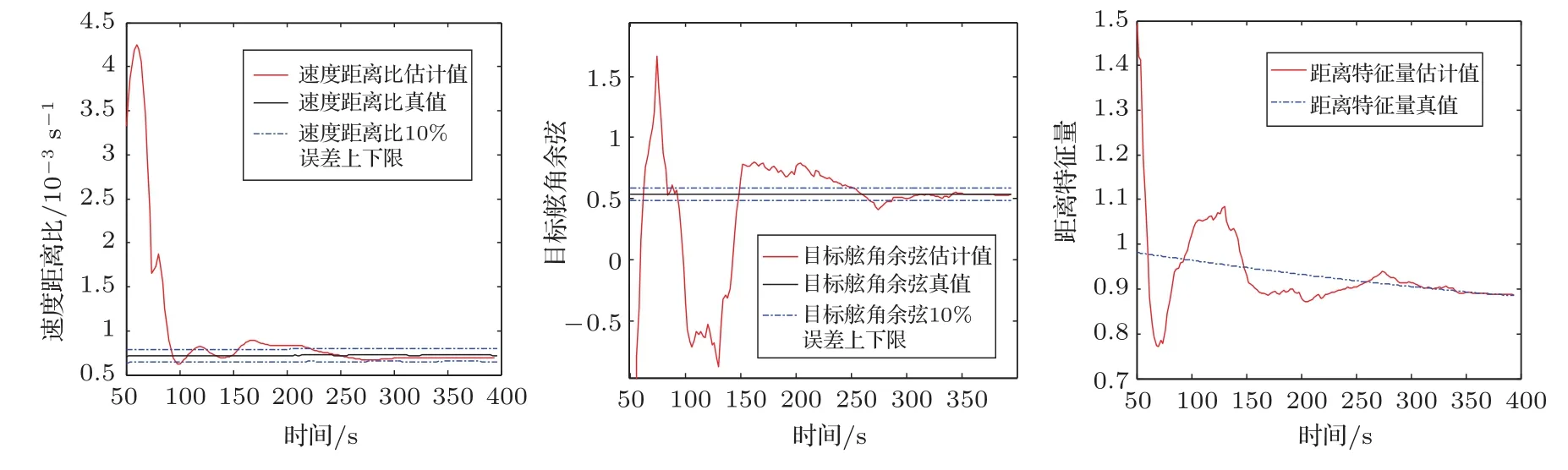
图11 表2序号2的计算结果Fig.11 Calculation results of No.2 in Table 2
5 结论
针对目标辐射噪声的LOFAR图中的干涉条纹模糊或缺失时,目标距离信息无法提取问题,讨论了匀速直线运动的声源目标和观测站条件下,仅利用方位信息估计距离特征量的方法。数值仿真和实验验证表明了该方法具有良好的稳定性,此外,该方法克服了观测站机动的限制,有利于观测站的隐蔽,这为目标定位的研究提供了一种新思路。
在实际数据的验证中,我们发现不同时间段的方位观测值的噪声特性是不同的,如何将这种不同噪声特性体现在解算的模型中,这也是需要进一步研究的问题。
致谢感谢预研基金项目(9140A03060213JB15039)的支持,感谢海军潜艇学院环境所提供的实际数据。
[1]SOSTRAND K A.Range localization of 10-100 km explosions by means of an endfire array and a waveguide Invariant[J].IEEE Journal Oceanic Engineering,2005,30(1):207-212.
[2]THODE A M.Source ranging with minimal environmental information using a virtual receiver and waveguide invariant theory[J].The Journal of the Acoustical Society of America,2000,108(4):1582-1594.
[3]COCKRELL K L,SCHMIDT H.Robust passive range estimation using the waveguide invariant[J].The Journal of the Acoustical Society of America,2010,127(5):2780-2789.
[4]ZHAO Zhendong,WANG Ning,GAO Dazhi,et al. Broadband source ranging in shallow water using the Ω-interference spectrum[J].Chinese Physics Letters,2010,27(6):1-4.
[5]余赟,惠俊英,赵智勇,等.基于声场干涉结构的双水平阵(元)被动测距[J].声学学报,2012,37(4):440-447. YU Yun,HUI Junying,ZHAO Zhiyong,et al.Passive ranging based on acoustic field interference structure using double arrays(elements)[J].Acta Acustica,2012,37(4):440-447.
[6]余赟,惠俊英,赵安邦,等.波导不变量及双阵(元)被动测距方法研究[J].兵工学报,2011,32(3):274-280. YU Yun,HUI Junying,ZHAO Anbang,et al.Waveguide invariant and passive ranging using double elements[J]. Acta Armamentrii,2011,32(3):274-280.
[7]余赟,惠俊英,殷敬伟,等.基于波导不变量的目标运动参数估计及被动测距[J].声学学报,2011,36(3):258-264. YU Yun,HUI Junying,YIN Jingwei,et al.Moving target parameter estimation and passive ranging based on waveguide invariant theory[J].Acta Acustica,2011,36(3):258-264.
[8]徐国军.基于波导不变性的水下目标声源估距研究[D].青岛:海军潜艇学院,2012.
[9]赵建昕,笪良龙,徐国军,等.线性等式约束下的纯方位目标运动分析[J].应用声学,2014,33(2):120-129. ZHAOJianxin,DALianglong,XUGuojun,etal. Bearing-only target analysis with linear equality constraints[J].Journal of Applied Acoustics,2014,33(2):120-129.
[10]何青海,笪良龙,徐国军.动态加权的多频段距离特征量数据融合方法[J].应用声学,2012,31(5):372-378. HE Qinghai,DA Lianglong,XU Guojun.A fusion algorithm of distance characteristic feature based on dynamically allocating weights[J].Journal of Applied Acoustics,2012,31(5):372-378.
[11]笪良龙,何青海.基于图像扩散去噪的距离特征量提取研究[J].应用声学,2013,32(2):100-108. DA Lianglong,HE Qinghai.Research on extraction of distance characteristic feature based on image diffusion denoising method[J].Journal of Applied Acoustics,2013,32(2):100-108.
Analysis of distance characteristic variable solved based on bearings-only in shallow sea
ZHAO JianxinGUO WuhongDA LianglongXU Guojun
(Navy Submarine Academy,Qingdao 266071,China)
Range-frequency striations,which appearing in plots of low-frequency analysis and record(LOFAR)spectrum of target radiated noise,include the information of target motion parameters and environment variables.When missing the striations of LOFAR spectrum,the information of target distance will not be obtained.For a sound source target in shallow sea with constant velocity along a straight line,using the information of bearings-only,a supplementary method of estimating distance characteristic variable is given by constructing the relationship between distance characteristic variable and target bearings.Numerical results and experimental verification in shallow sea show that the method is feasible and effective.
Bearings-only,Distance characteristic variable,Velocity distance ratio
O428,TP391
A
1000-310X(2015)04-0320-13
10.11684/j.issn.1000-310X.2015.04.006
2014-07-14收稿;2015-03-24定稿
∗预研基金(9140A03060213JB15039)
赵建昕(1969-),男,山东青岛人,副教授,博士,研究方向:数据同化,目标跟踪。†
E-mail:qy_zjx@bit.edu.cn
