基于混合粒子滤波的水下小目标跟踪∗

许枫　纪永强，2†　郭占军　杨娟　苏瑞文，2

（1中国科学院声学研究所北京100190）（2中国科学院大学北京100049）（3海军海洋测绘研究所天津300061）

基于混合粒子滤波的水下小目标跟踪∗

许枫1纪永强1，2†郭占军3杨娟1苏瑞文1，2

（1中国科学院声学研究所北京100190）（2中国科学院大学北京100049）（3海军海洋测绘研究所天津300061）

针对水下小目标粒子滤波估计过程中“粒子贫化”引起的估计性能下降，提出了混合粒子滤波算法。该算法在常规粒子滤波算法基础上，在每一步迭代估计过程中进行量测的再次随机采样，以丰富随机粒子多样性，缓解水下小目标状态估计过程中的“粒子贫化”的影响。对算法进行了仿真分析，并将该方法用于水下小目标探测实验的数据处理。结果表明，相比于常规的粒子滤波算法，所提出的混合粒子滤波得到了误差更小且稳定的状态估计结果，有效地改善水下小目标跟踪的精度和稳健性。

目标跟踪，水下小目标，混合粒子滤波，粒子贫化，量测采样

1　引言

蛙人、水下机器人等水下小目标的弱散射特性、非对称性等特点使其成为影响海事设施安全的重要因素。针对水下小目标探测的研究日益成为国内外水下安防领域的热点［1-2］。其中，水下小目标跟踪技术是蛙人探测声纳技术的基础，是进一步实现水下运动小目标识别及处置的基础。目标跟踪状态估计精度主要受三方面因素影响：状态估计算法、目标运动模型、传感器精度及测量方式，而状态估计算法是影响目标状态估计精度的重要因素，本文从状态估计算法的角度改进水下运动小目标跟踪性能。

常用的目标状态估计方法是卡尔曼滤波方法，该方法可得到线性高斯情形下的无偏最小均方误差估计。在蛙人、水下机器人等目标运动的实际过程中，很难保证系统是线性系统且具有高斯噪声。由于粒子滤波方法在处理非线性、非高斯系统的状态估计问题中的独特优势，本文利用粒子滤波方法实现水下运动小目标的状态估计。

虽然粒子滤波方法可作为目标状态估计的有效手段，但粒子滤波方法的重采样过程造成随机样本的多样性和有效性的降低，极易造成估计性能的下降甚至发散［3］。为了解决重采样带来的粒子贫化问题，Gordon等人提出对每个样本点增加高斯扰动，将马尔可夫链蒙特卡罗MCMC（Markov Chain Monte Carlo）引入粒子滤波算法中，该方法在改善粒子多样性的同时，也极大地增加了算法的运行时间［4］。Seongkeun Park等将遗传算法引入到粒子滤波算法中，有效地抑制了粒子贫化，改善粒子滤波的估计性能［5］。Ming Li进一步将遗传算法和粒子蚁群算法用于粒子滤波算法的改进，提高了粒子样本的多样性［6］。Tiancheng Li等通过确定重采样的方法，避免了低权重随机粒子的剔除，缓解了传统粒子滤波过程中的“粒子贫化”现象［7］。在粒子聚集的一定邻域内抽取产生新的粒子，也可降低多样性损失带来的粒子贫化现象。在机器人跟踪问题中，Vadakkepat通过在传统粒子滤波基础上，在传感器目标观测位置周围进行随机采样，以改善粒子多样性，提高机器人状态估计性能［8］。

针对常规粒子滤波的“粒子贫化”对水下小目标状态估计性能的影响，本文提出了混合粒子滤波方法。该方法对声纳的观测进行随机采样以提高采样样本的多样性，最终达到改善水下目标跟踪状态估计性能的目的。本文将混合粒子滤波算法用于蛙人探测实验的数据处理，并与常规粒子滤波算法的估计性能进行了对比。结果表明，与常规粒子滤波算法相比，本文提出的混合粒子滤波方法的蛙人状态估计效果精度更高、稳定性更好。

2　混合粒子滤波算法

粒子滤波是基于蒙特卡罗思想和贝叶斯最优估计理论的状态估计方法。贝叶斯估计将目标的状态估计转换为后验概率p（zk|Zk）的计算，进而通过一定的估计准则得到目标状态的最优估计。为避免贝叶斯估计中的复杂积分运算，粒子滤波方法通过蒙特卡罗思想利用采样的统计方法描述整个空间的概率分布，将复杂的积分问题转化为有限随机样本的加权求和问题，如图1所示。

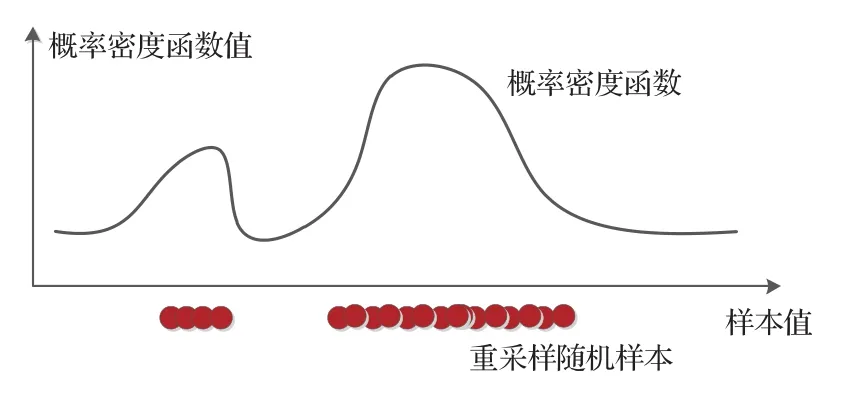
图1　概率密度分布的采样粒子表示Fig.1 The representation of sampling particles for probability density distribution

2.1常规粒子滤波算法

粒子滤波状态估计方法以贝叶斯估计理论为基础，根据起始时刻到k时刻的目标观测集求得k时刻目标状态Xk后验概率分布进一步根据概率分布完成目标状态Xk的估计。

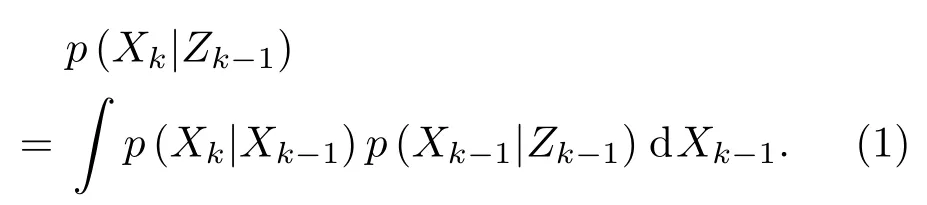
更新：根据传感器得到的目标观测Zk=由贝叶斯规则按式2完成后验概率的更新。

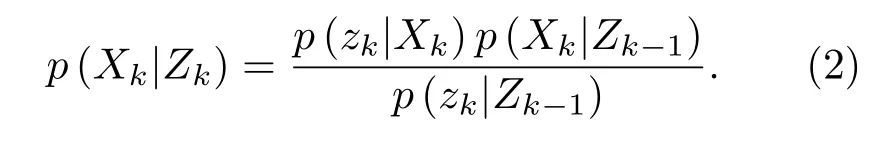
为避免贝叶斯估计中复杂的积分运算，粒子滤波方法借助蒙特卡罗思想利用符合一定分布规律随机粒子集表征后验概率。设从后验概率密度p（xk|Zk）中抽取N个独立同分布的随机样本z（s），s=1，···，N，则后验概率分布p（Xk|Zk）可近似逼近，如式（3）所示。

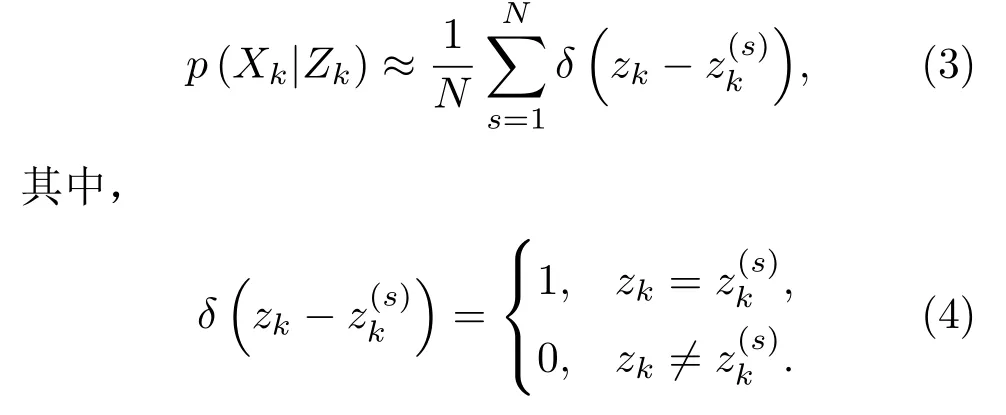
粒子滤波算法包括初始化、预测、更新和粒子重采样等步骤，具体如下［10］。

（1）初始化：根据初始时刻探测结果的先验概率分布进行随机采样，生成N个随机粒子并将随机权值设为

（2）预测：根据目标运动模型f，将k-1时刻的随机粒子递推到k时刻的预测粒子。

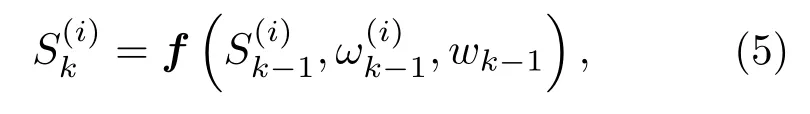
式（5）中，i=1，2，···，N。N表示随机粒子的数目。

（3）更新：通过传（感器得到）的目标观测，得到所有粒子的似然函数，进一步得到预测粒子的归一化权重，最终通过随机粒子的加权求和处理完成目标状态Xk的粒子滤波估计，如式（6）∼（8）所示。

（4）重采样：复制大权重粒子，去除小权重粒子，并对重采样后的粒子赋予相同的权值。

（5）重采样结束后，判断是否退出本算法，否则转向步骤2。

粒子滤波重采样处理，在一定程度上抑制了多次迭代过中粒子退化发散引起的估计性能下降，但不可避免的是，重采样过程保留高权重粒子的同时剔除了低权重粒子，在一定程度上降低了粒子多样性，引起粒子贫化，造成水下小目标状态估计性能的下降甚至发散［11］。

通过上述粒子滤波步骤可发现，常规粒子滤波只在初始化步骤产生随机粒子。在后面的迭代滤波估计过程中，初始化生成的粒子在每次迭代估计过程中传播，并没有生成新的粒子，最终导致多次递推过程后粒子多样性降低，粒子空间分布偏差越来越大，进而造成状态估计性能的下降。

2.2混合粒子滤波算法

重采样算法是粒子滤波算法的重要步骤，是解决粒子滤波算法退化问题的重要手段，但同时也带来了粒子贫化问题。针对粒子贫化造成的水下小目标状态粒子滤波估计性能下降的问题，本文在常规粒子滤波初始化得到随机粒子的基础上，在每一步迭代估计过程中，对目标量测再次进行随机采样，以改善粒子的多样性，最终实现水下小目标高精度、高稳健性的状态估计［10，12］。

根据k时刻传感器得到的目标量测及先验概率分布对目标量测再次进行随机采样，生成M个随机粒子。

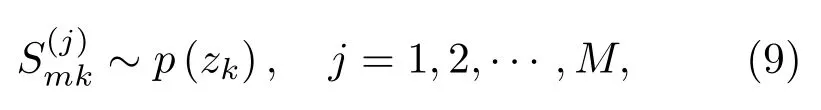
根据公式（2）并结合目标运动规律得到k时刻预测粒（子位置分布，）计算目标量测采样粒子的似然函数，根据似然函数进一步求得目标量测采样粒子的权重，如式（10）所示。

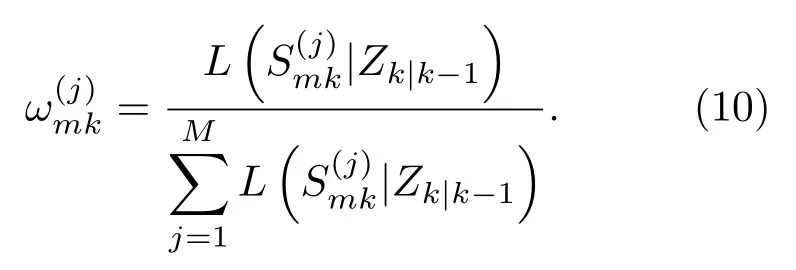
在计算求得各类型粒子权重后，根据式（11）对所有粒子进行加权求和，最终得到混合粒子滤波的目标状态估计。

在混合粒子滤波的重采样阶段，对全部粒子的权重排序，剔除权重较小的随机粒子，保留N个随机粒子，然后转向下一次迭代运算。

混合粒子滤波的流程框图如图2所示。图2中，虚线框表示了混合粒子滤波算法中，通过目标观测的随机采样改善粒子多样性的过程。

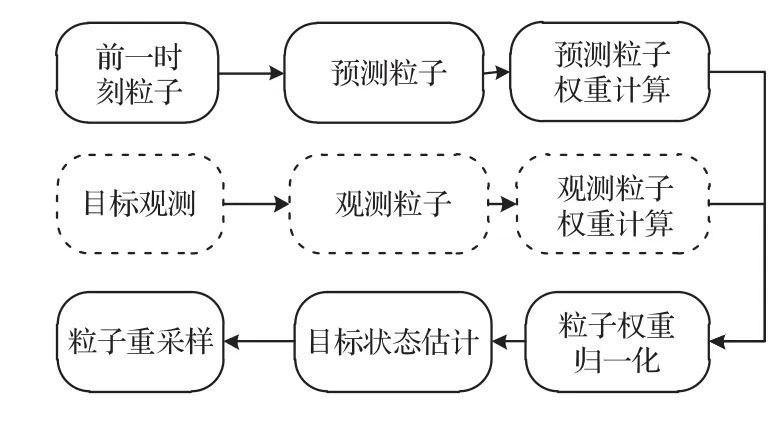
图2　混合粒子滤波状态估计框图Fig.2 Flowchart of state estimation by mixture particle filter

3　仿真分析

为验证混合粒子滤波算法的有效性，分别对混合粒子滤波算法和常规粒子滤波算法仿真，并将仿真结果进行比较。仿真参数如表1所示。

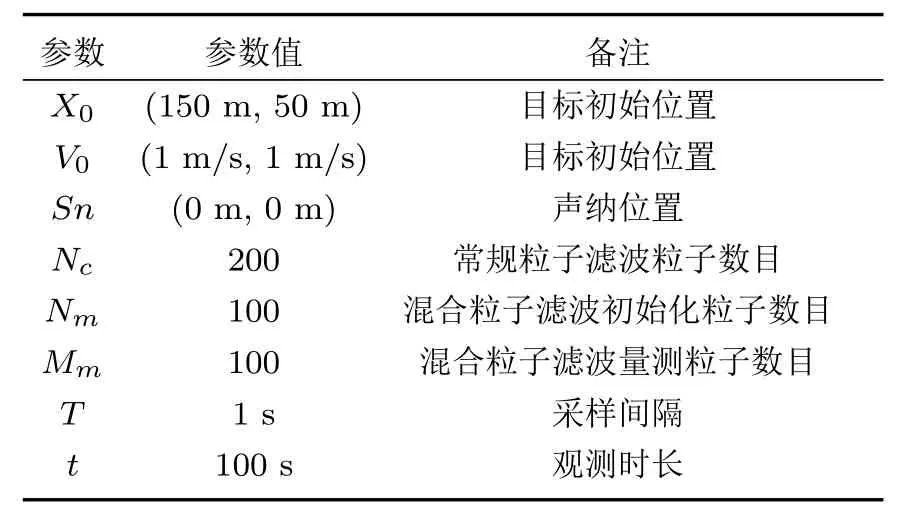
表1　仿真过程中的参数说明Table 1The parameter settings for the simulation

为比较不同算法的状态估计性能，将多次Monte Carlo仿真处理得到的目标位置估计结果的均方根误差（Root mean square error，RMSE）作为衡量估计性能的指标，均方根误差的公式如式（12）所示。

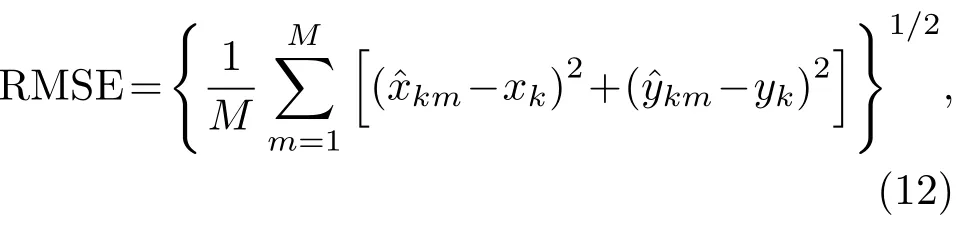
图3是经100次Mont Carlo仿真后的目标状态估计结果，图4是不同滤波的滤波算法及声纳观测航迹与目标真实位置的均方根误差，可看出混合粒子滤波算法的状态估计精度更高、稳定性更好。

由仿真结果可看出，相比于常规粒子滤波算法，混合粒子滤波算法可得到精度更高、稳定性更好的目标状态估计。这是因为混合粒子滤波算法通过对量测的随机采样处理，丰富了粒子滤波过程中粒子的多样性，有效缓解了重采样过程带来的“粒子贫化”问题。

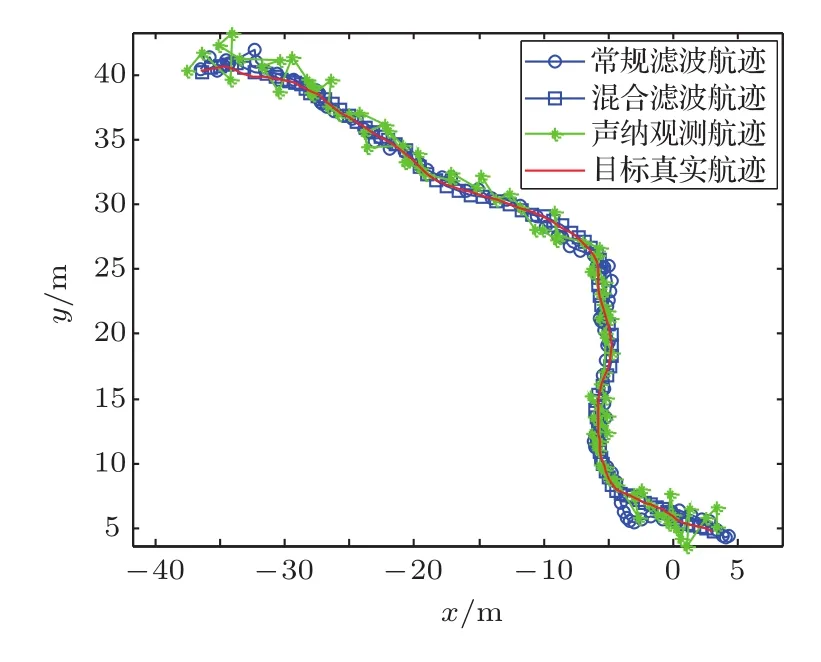
图3　不同粒子滤波方法的状态估计结果Fig.3 The state estimation by the different particle filters

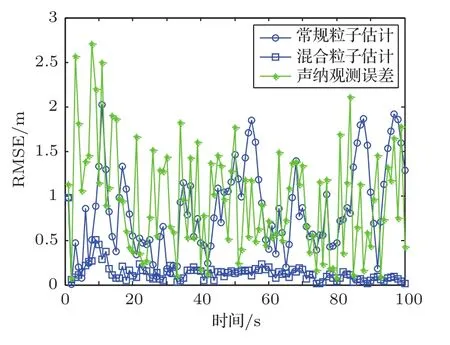
图4　不同粒子滤波方法状态估计的均方根误差Fig.4 The RMSE of state estimation by different particle filters

4　实验数据处理

4.1实验概述

2013年4月，在海南一近岸水域进行了水下运动小目标的多基地探测实验。实验过程中，水下小目标的多基地探测系统通过3部蛙人探测声纳的改进升级实现，3个声纳节点位于同一直线上，被探测的水下小目标是开式蛙人。发射端声纳发射的声信号经蛙人目标的散射作用被接收端声纳接收，为了系统校准及提高小目标探测概率，发射端声纳也接收水下小目标的回波。多基地系统的同步接收的时间间隔为3 s，时间同步由GPS时间信号出发完成。为了便于小目标的融合跟踪，建立了以发射端声纳S1为原点，以各声纳节点所在直线为x轴建立公共坐标系。图5是某航次实验中GPS接收机记录水下小目标的运动航迹。其中，红线区域是发射端声纳S1的作用区域，蓝线区域是接收端声纳R1和R2的作用区域，绿线表示的目标运动过程中GPS观测航迹。

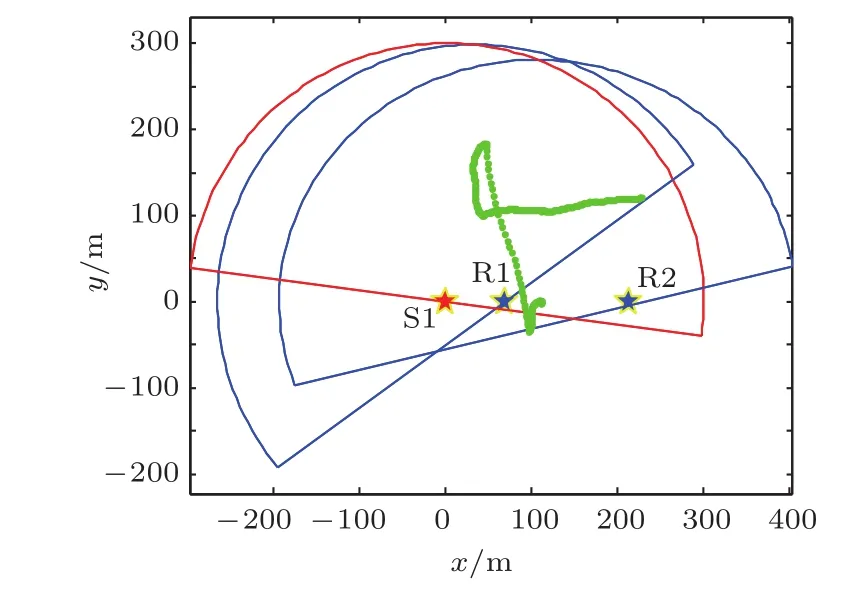
图5　水下小目标多基地跟踪试验布局图Fig.5 Ground truth plot and sonar layout for the realistic experiment

4.2数据处理结果

由于多基地声纳可同步得到小目标的多角度观测数据，这里将多基地系统目标量测经融合处理后得到的系统量测作为目标状态更新的观测值。将常规粒子滤波方法和混合粒子滤波方法分别用于实验数据的处理。水下小目标多基地探测实验数据经不同粒子滤波处理后的状态估计结果如图6所示，不同方法得到的目标位置估计的均方根误差如图7所示。

由图6∼7可知，相比于常规粒子滤波方法，混合粒子滤波方法得到了更高精度、更优稳健性的状态估计结果。

为进一步分析常规粒子滤波和混合粒子滤波方法的性能，这里分别按式13和14对不同滤波对一段时间内目标位置估计结果的均方根误差进行了均值和方差统计特性分析，得到了如表2所示的数字统计特征。

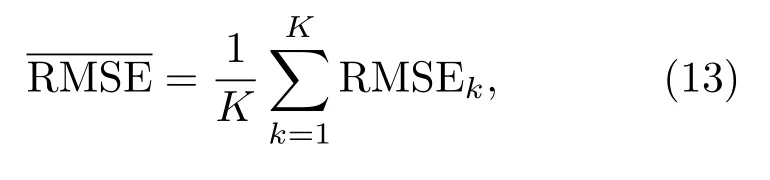
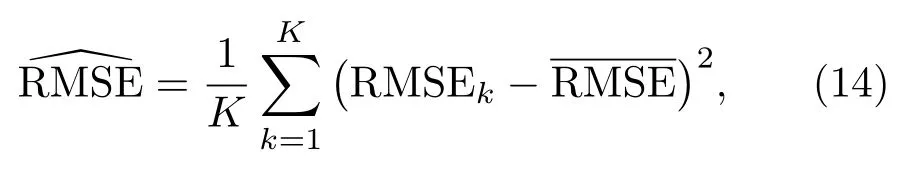
式（14）中，RMSEk是k时刻M次滤波估计结果的均方根误差。

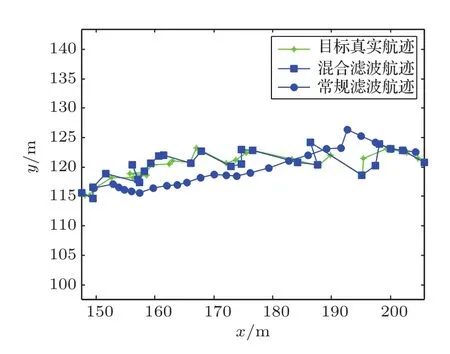
图6　不同粒子滤波的水下小目标状态估计结果Fig.6 The underwater small target state estimation with the different particle filters

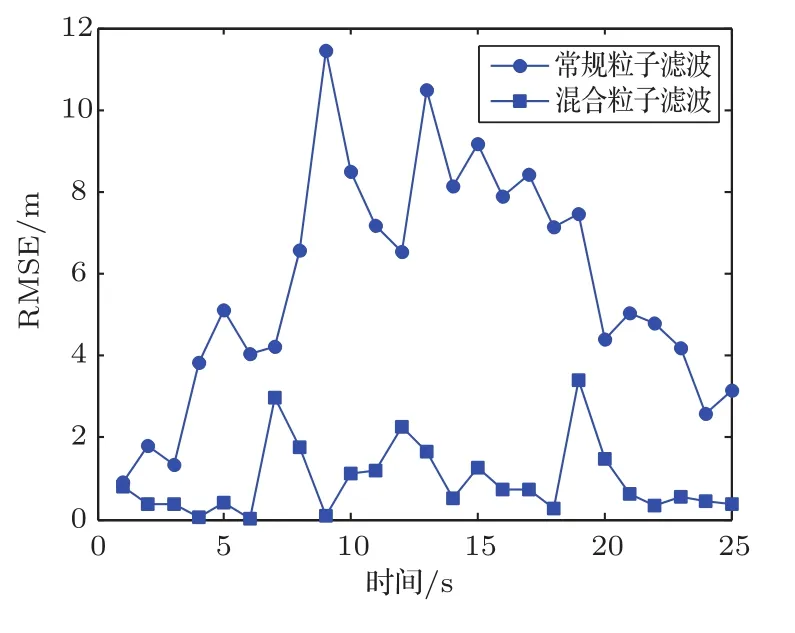
图7　不同粒子滤波状态估计的均方根误差Fig.7 The RMSE of state estimation with the different particle filters

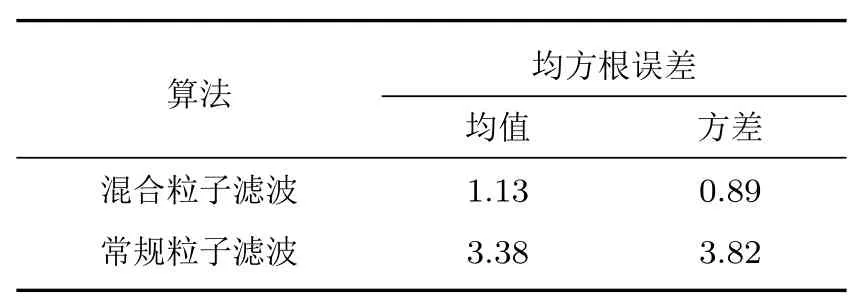
表2　不同粒子滤波状态估计均方根误差的统计分析结果Table 2 The statistical analysis results of RMSE for state estimation by the different particle filters

由表2可看出，混合粒子滤波算法均方根误差的均值和方差均小于常规粒子滤波算法，表明混合粒子滤波在水下小目标状态估计性能方面明显优于常规粒子滤波算法。

5　结论

针对水下小目标粒子滤波状态估计过程中，粒子多样性的降低造成的估计性能下降的问题，本文提出了混合粒子滤波方法。混合粒子滤波在常规粒子滤波初始化生成粒子基础上，在每次迭代估计过程中对目标量测再次进行随机采样，以丰富粒子多样性，有效改善了水下小目标粒子滤波状态估计性能。对比常规粒子滤波算法，对混合粒子算法进行了仿真分析，并将算法分别用于水下小目标多基地探测实验的数据处理。结果表明，相比于常规粒子滤波方法，混合粒子滤波算法有效缓解了粒子贫化的影响，得到了水下小目标精度更高、稳健性更优的状态估计结果。

［1］RADU O，SLAMNOIU G，ZARNESCU L，et al.Harbor protection against terrorist threats：Difficulties and possible solutions［R］.2006：1-10.

［2］CRAWFORD A，PERCIVAL A，CROWE V.Use of small imaging sonars for diver identification［C］.IEEE International Conference on Technologies for Homeland Security（HST），IEEE，2011：262-266.

［3］LIM J.Performance degradation due to particle impoverishment in particle filtering［J］.Journal of Electrical Engineering&Technology，2014，9（6）：2107-2113.

［4］GORDON N J，SALMOND D J，SMITH A F M.Novel approach to nonlinear/non-Gaussian Bayesian state estimation［J］.IEEE Proceedings of Radar and Signal Processing，1993，140（2）：107-113.

［5］PARK S，HWANG J P，KIM E，et al.A new evolutionary particle filter for the prevention of sample impoverishment［J］.Transactions on Evolutionary Computation，2009，13（4）：801-809.

［6］LI M，PANG B，He Y F，et al.Particle filter improved by genetic algorithm and particle swarm optimization algorithm［J］.Journal of Software，2013，8（3）：666-672.

［7］LI T C，SATTAR T P，SUN S D.Deterministic resampling：Unbiased sampling to avoid sample impoverishment in particle filters［J］.Signal Processing，2012，92（7）：1637-1645.

［8］PRAHLAD V，LIU J.Improved particle filter in sensor fusion for tracking randomly moving object［J］.IEEE Transactions on Instrumentation and Measurement，2006，55（5）：1823-1832.

［9］DELLAERT F，FOX D，BURGARD W，et al.Monte Carlo localization for mobile robots［C］.IEEE International Conference on Robotics and Automation，1999，（2）：1322-1328.

［10］JENSFELT P，WIJK O，AUSTIN D，et al.Experiments on augmenting condensation for mobile robot localization［C］.Proceedings of IEEE International Conference Robot Automation，2000，（3）：2518-2524.

［11］BAIN A，CRISAN D.A continuous time particle filter［J］. Applications of Mathematics，2009，60：221-256.

［12］JENSFELT P.Approaches to mobile robot localization in indoor environments［D］.Dept.Signal，Sensors and Systems（S3），Royal Institute of Technology，Stockholm，Sweden，2001.

Underwater small target tracking based on mixture particle filter

XU Feng1JI Yongqiang1，2GUO Zhanjun3YANG Juan1SU Ruiwen1，2
（1 Institute of Acoustics，Chinese Academy of Sciences，Beijing 100190，China）（2 University of Chinese Academy of Sciences，Beijing 100049，China）（3 Naval Institute of Hydrographic Surveying and Charting，Tianjin 300061，China）

In order to solve the problem of estimation performance degradation caused by particle impoverishment for underwater small target tracking，the mixture particle filter is proposed.The target measurements are resampled based on the conventional particle filter to reduce the influence of the particle impoverishment in every iterative estimation step due to enriching particle diversity.The simulated analysis of the proposed algorithm was conducted，while the algorithm was also utilized for the underwater small target detection experimental data processing.The results show that the mixture particle filter algorithm acquires state estimation with more stability and less error comparing to conventional particle filter.The mixture particle filter is effective to improve accuracy and stability for underwater small target tracking.

Target tracking，Underwater small target，Mixture particle filter，Particle impoverishment，Measurement sampling

TN953

A

1000-310X（2015）04-0297-06

10.11684/j.issn.1000-310X.2015.04.003

2014-12-16收稿；2015-02-16定稿

∗国家自然科学基金项目（10904159，11404365）

许枫（1969-），男，浙江宁波人，研究员，博士生导师，研究方向：水声信号处理。†

E-mail：ioajiyq@163.com