自润滑活塞环导热特性研究

王赛苗，郑苏录，王向平，毛云雁，彭学院

（1.西安交通大学能源与动力工程学院，陕西西安710049；2.衡州市质量技术监督检测中心，湖南衡阳324000）

自润滑活塞环导热特性研究

王赛苗1，郑苏录2，王向平2，毛云雁2，彭学院1

（1.西安交通大学能源与动力工程学院，陕西西安710049；2.衡州市质量技术监督检测中心，湖南衡阳324000）

针对自润滑活塞环的摩擦热失效问题，通过建立二元填充体系导热系数计算有限元模型，研究了18组不同配方填充材料对自润滑活塞环导热系数的影响。研究结果表明复合材料导热系数与填料相含量成正比；填充颗粒形状及取向对复合材料导热系数影响较大，沿热流方向的颗粒特征长度越大，复合材料导热系数就越高。

自润滑活塞环；PTFE；导热系数

1　引言

气体的无油压缩既保证了气体的洁净又避免了繁琐的油路循环系统。往复压缩机普遍采用自润滑的活塞环来实现气缸无油。作为往复活塞压缩机的主要易损件之一，活塞环的工作状况直接影响压缩机的经济性与可靠性。在压缩机行业中常采用PTFE等聚合物材料来制作自润滑活塞环，但这类聚合物耐高温能力弱，在高温工况下易热失效。因此，增强自润滑材料导热系数对降低活塞环摩擦热效应具有重要意义［2］。

关于聚合物基复合材料导热性能的分析已受到特别关注［3-8］，针对聚四氟乙烯材料导热系数小的缺点，国内外多名学者对改善PTFE材料性能进行了研究。梁基照等［9］建立了PPS/CaCO3填充体系的单胞简化模型，研究证明有效热导率模拟值和计算值较为接近，且随CaCO3体积分数的增加线性增加；解挺等［10］对不同含量铜粉颗粒均匀分布于PTFE基复合材料的填充二元体系有效热导率进行了二维有限元分析，模拟结果与实验结果的对比验证了有限元模拟的可靠性；孙爱芳等［11］建立了石墨/PTFE复合材料的二维多颗粒随机分布模型，通过与实验数据对比，发现石墨含量较低时，模拟结果与实验值较为吻合，石墨含量较高时，有限元结果低于实验值；涂善东等［12］通过建立石墨/PTFE复合材料二元体系的颗粒随机分布模型和均匀分布模型，发现颗粒分布的不均匀性会降低材料导热系数；蔡立芳等［13］研究了经聚苯酯改性的PTFE基复合材料的导热及摩擦学性能，结果表明含填料量为5%的PTFE基复合材料导热性能显著提高。Kumlutas等［14］采用三维模型模拟了不同含量锡颗粒填充聚合物材料的微观结构，发现复合材料的导热系数随锡体积含量增加呈指数增长，但增加到一定值时与实验值差别较大。综上所述，通过填充导热性能强的无机粒子来增强这类自润滑材料的摩擦热导出能力，是提高其耐高温性能的有效办法。

本文建立了二元填充体系导热系数计算有限元模型，设计了18组不同种类和配比的填充相所构成的二元填充复合材料体系，研究了不同填充材料对自润滑活塞环导热系数的影响，分析了填充颗粒种类、含量、以及颗粒形状对复合材料导热系数的影响。

2　二元填充体系导热系数计算有限元模型

2.1自润滑活塞环材料组分的设计

本文将石墨（GR）、玻璃纤维（GF）和碳纤维（GF）分别以不同含量加入聚四氟乙烯（PTFE）中，构成二元填充复合材料体系，具体配方见表1。

2.2填充聚合物基自润滑活塞环材料导热系数的数值模拟

按导热增强填料在聚合物基体中不同的分布方式可以建立2种不同的几何模型。

（1）周期性均匀分布单胞模型。复合材料的周期性均匀单胞模型及其二维热传导模型如图1所示，有限元模型如图2所示。

表1　二元填充体系组分配方

图1　复合材料的周期性均匀单胞模型及其二维热传导模型

（2）多颗粒随机分布模型。多颗粒随机分布模型的几何模型和有限元模型如图3所示。

图2　单胞单元体有限元模型

2.3二元填充体系导热系数模拟模型的验证

本文选择以下2种方法，验证所采用的有限元计算模型的合理性：

首先，针对5wt%石墨填充PTFE自润滑复合体系，分别对单胞模型和多胞模型施加不同热载荷和对流边界条件后，进行了模型求解，各边界条件下计算得到的导热系数值如表2所示。

可以看出，单胞模型和多胞随机分布模型，对设定的3组不同的载荷与边界条件导热系数计算值是相同的。

天空部分，我选择了渐变滤镜工具，单击曝光滑块前方的减号将其设置为-0.50，其余所有选项也在同时被归零。我从上到下绘制了若干个渐变条，逐步压暗天空。对效果满意之后，我又创建了一个曝光设置为+0.50的渐变，从下往上拖动提亮前景。

图3　多胞随机分布几何模型及有限元模型

表2　边界条件对导热系数模拟值的影响

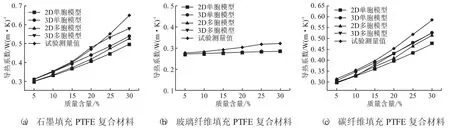
图4　不同模型下单元体平均导热系数模拟值与实验值的对比

其次，采用TC3000导热系数仪对自润滑活塞环的导热系数进行了测定［15］。图4为采用不同计算模型时，不同含量的石墨、玻璃纤维和碳纤维填充聚四氟乙烯复合材料的平均导热系数模拟结果与实验结果的对比图。

对于填料相含量为30%的复合体系，填充相分别为石墨、玻璃纤维和碳纤维时，三维随机分布模型模拟值与实验值误差分别为12.6%、13.3%和11.4%。对于3种填料填充的PTFE基复合材料，随着填充相含量的增加，材料平均导热系数模拟值与测量值误差均增加，这种现象是因为在建立有限元模型时，假设填充相在基体中是完全分散的，即完全采用“孤岛模型”，没有考虑填充相在基体中可能会出现的团聚、成链等情况，在模型内部填充相不能形成有效的导热网链，而随着填充含量的增加，填充相在基体中出现团聚、成链情况的可能性会增加，从而导致误差的放大。模拟值与实验值存在误差的原因可能为实验中所用的样品基体材料与填充相颗粒未能完全混合均匀，其微观结构与有限元模型存在差异。但是考虑到在填充范围内，有限元计算与实验结果的变化趋势完全一致，采用有限元方法来定性研究填充相对自润滑复合材料导热系数影响规律的研究是可行的。

以上两方面实验与模拟结果的比较，验证了单胞模型和多胞模型用于模拟二元填充体系导热系数的合理性。考虑到2种模型均合理，由于单胞模型较多胞模型网格划分简单，计算时间短，故本文采用单胞模型。

2.4填充相的加入对单胞模型的温度场和导热能力的影响

为了研究填充相的加入对单胞模型温度场和导热能力的影响，以5wt%石墨填充PTFE复合材料的球形粒子为例，模拟得到的温度场分布如图5所示。可以看出，单胞模型的温度分布从上表面到下表面大幅下降，但不是均匀递减的，而是与石墨粒子在基体中的位置和大小有关，热量由模型上表面传入模型中，遇到位于中心的球形颗粒后，靠近填料的区域温度变化较小，而其它区域温度梯度较大，这是由于填充相与基体材料的物性参数不同，且石墨导热系数远大于聚四氟乙烯的导热系数，热量在石墨颗粒内部能够迅速扩散的缘故。

单元体在沿距离球心不同距离的各路径上纵向节点的温度分布情况如图6所示。可以看到，在距离微球体球心最远的A路径上，两端面温差最大达到78.38℃，在通过球心的D路径上，上下端面温差最小只有76.74℃，越靠近球心的路径上，上下端面温差越小；且在球体外部温度迅速下降，而在球体内部温度下降缓慢，几乎呈水平直线。这表明石墨颗粒内热阻较小，能够有效提高聚四氟乙烯材料的导热系数。

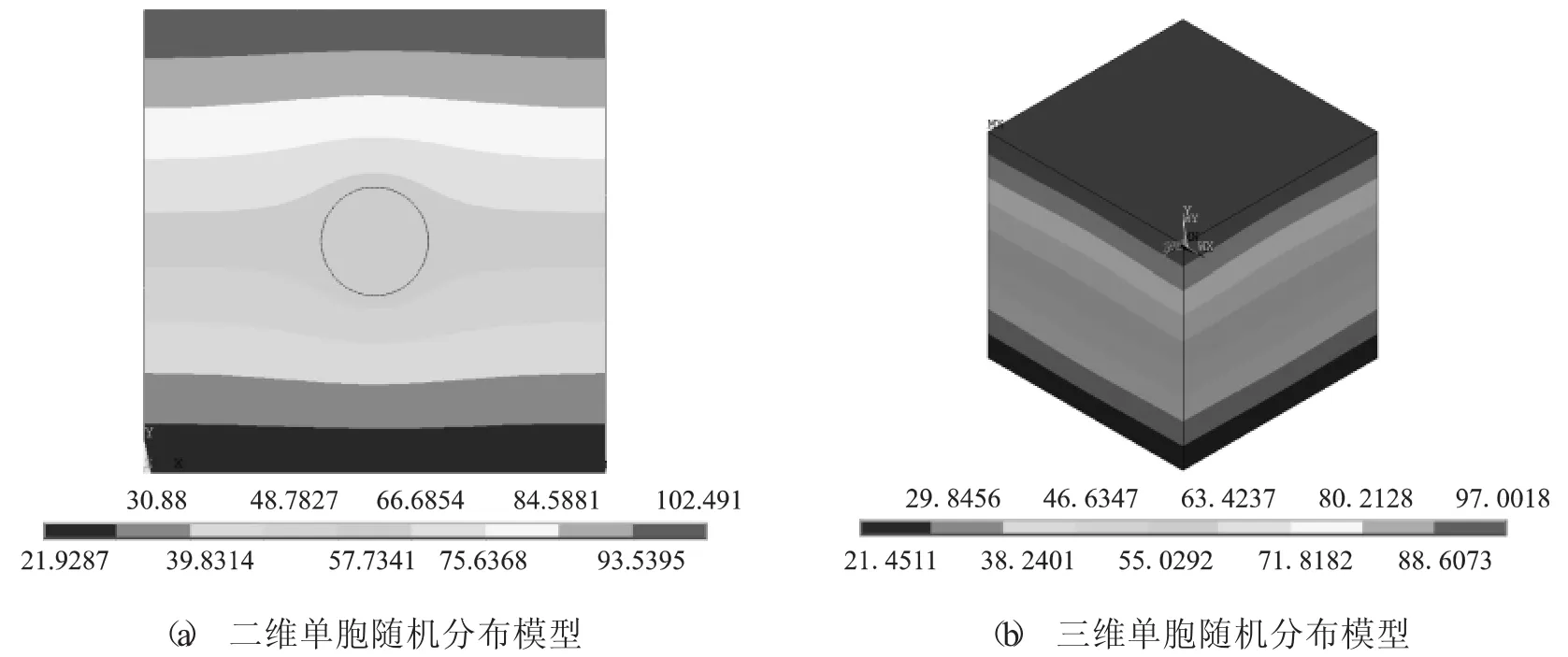
图5　2种有限元模型温度场分布情况

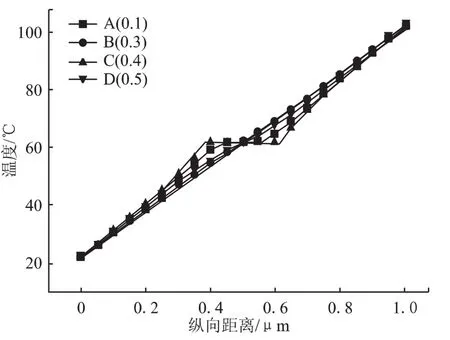
图6　单胞模型单元体节点温度随纵向距离变化曲线

3　二元填充体系导热系数影响因素分析

3.1填充相形状的影响

当填充颗粒形状为球形、正方体、长方体和圆柱体4种规则形状时，用有限元方法计算了不同单元体的导热系数。规定平行于长方体长边所在面的方向和沿圆柱体轴向为纵向，平行于长方体短边所在面的方向和平行于圆柱体底面的方向为横向。文中热流密度均沿横向施加。图7为填充相颗粒形状不同时各单元体的等效导热系数计算值。

可以看出，在填充相含量相同时，填充颗粒形状为正方体时，填充体系导热系数最大，填充颗粒形状为长方体时，填充体系导热系数最小。且随着填充颗粒含量的增加，含有的填充颗粒形状不同的填充体系导热系数均提高，但增幅不同，正方体颗粒体系增幅最大，达52.03%，长方体增幅最小，仅有32.59%。

3.2填充相颗粒取向的影响

本文采用填充颗粒形状分别为长方体和长径比为2的圆柱体填充模型，分别沿纵向和横向2个方向施加热流密度载荷。图8中（a）和（b）分别表示长方体填充相和圆柱体填充相在不同排列方式下复合材料导热系数的区别。

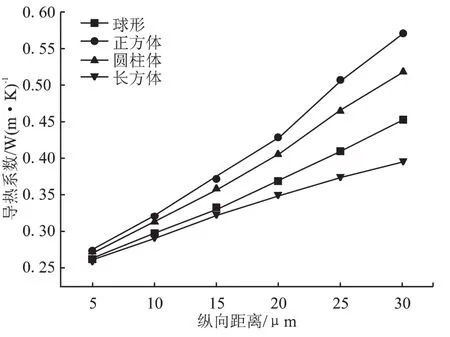
图7　填充相颗粒形状不同时各单元体的等效导热系数计算值

图8　导热系数与填充相排列方式的关系

可以看出，对于填料形状不同的2种填充体系，填充颗粒纵向分布时体系的导热系数均大于横向分布时的导热系数，并且随着填充含量的增加，由颗粒取向造成的同一填充体系导热系数的差值也扩大。可见沿热流方向的颗粒特征长度越大，复合材料导热系数越高。

3.3填充相种类的影响

图9对不同填料的导热增强效果作了对比。

可以看出，石墨、碳纤维和玻璃纤维3种填充料的添加均可提高自润滑复合材料的导热系数，且随着填充量增加，复合材料导热系数均随之增加。石墨含量对复合材料的导热系数影响最大，碳纤维次之，玻璃纤维影响最小，当填充含量为30 wt%时，填充石墨、碳纤维和玻璃纤维分别比未填充材料的导热系数提高109.09%、72.73%和4.73%。

图9　填料种类对PTFE复合材料的导热系数的影响

4　结论

本文针对自润滑活塞环的摩擦热失效问题，设计了18组不同种类和配比的填充相所构成的二元填充复合材料体系，对自润滑活塞环的导热特性进行了研究，通过有限元方法研究了不同填充材料对自润滑活塞环导热系数的影响，具体结论如下：

（1）建立了二元填充体系导热系数计算有限元模型，发现采用三维模型时导热系数的计算值与实验值较为吻合。当石墨、玻璃纤维和碳纤维填充含量低于15wt%时，二元填充体系导热系数有限元模型能够较准确的计算不同组成配比复合材料的导热系数，最大误差为0.88%。

（2）在填充相含量相同时，填充颗粒形状为正方体时，填充体系导热系数最大，填充颗粒形状为长方体时，填充体系导热系数最小。且随着填充颗粒含量的增加，含有的填充颗粒形状不同的填充体系导热系数均提高，但增幅不同，正方体颗粒体系增幅最大，达52.03%，长方体增幅最小，仅有32.59%。

（3）对于填料形状不同的2种填充体系，沿热流方向的颗粒特征长度越大，复合材料导热系数越高。

（4）石墨、碳纤维和玻璃纤维3种填充料的添加都能够提高自润滑复合材料的导热系数，且随着填充量增加而增加。石墨含量对复合材料的导热系数影响最大，碳纤维次之，玻璃纤维影响最小。当填充含量为30 wt%时填充石墨、碳纤维和玻璃纤维分别比未填充材料的导热系数提高109.09%、72.73%和4.73%。

［1］刁玉辉，韦安和.自润滑活塞环的摩擦磨损分析［J］.润滑［2］辛电波，邬晓霞.自润滑活塞环的压力分布及摩擦热研究［J］：西安交通大学，2010.

与密封，2004，（5）.

［3］Song YS，Youn JR.Evaluation of Effective Thermal Conductivity for Carbon Nanotube/polymer Composites Using ControlVolumeFiniteElementMethod［J］.Carbon，2006，44（4）：710-717.

［4］Zawada T.Simultaneous Estimation of Heat Transfer Coefficient and Thermal Conductivity with Application to Microelectronic Materials［J］.Microelectronics Journal，2006，37（4）：340-352.

［5］Jeng MS，Yang R，Song D，et al.Modeling the Thermal Conductivity and Phonon Transport in Nanoparticle Composites Using Monte Carlo Simulation［J］.Journal of Heat Transfer，2008，130（4）.

［6］Guoqing Z，Yanping X，Hui W，et al.A Percolation Model of Thermal Conductivity for Filled Polymer Composites［J］. Journal of Composite Materials，2009，44（8）：963-970.

［7］Zhang Q，Pi Z，Chen M，et al.Effective Thermal Conductivity of Silicone/phosphor Composites［J］.Journal of Composite Materials，2011，45（23）：2465-2473.

［8］Mu L，Shi Y，Feng X，et al.The Effect of Thermal Conductivity and Friction Coefficient on the Contact Temperature of Polyimide Composites：Experimental and Finite Element Simulation［J］.Tribology International，2012，53：45-52.

［9］梁基照，刘冠生.无机粒子填充聚合物复合材料传热模型及有限元模拟［J］.特种橡胶制品，2006，27（5）：4.

［10］解挺，林子钧，陈刚，等.Cu粉含量对PTFE基复合材料导热性能影响的数值分析［J］.金属功能材料，2010，17（2）.

［11］孙爱芳，刘敏珊，董其伍.石墨/PTFE复合材料导热性能的数值模拟［J］.材料科学与工程学报，2007，25（3）：4.

［12］涂善东，殷勇，凌祥.石墨改性聚四氟乙烯导热系数的研究［C］.苏州，2001：46-51.

［13］蔡立芳，梁新，董华东，等.不同填料增强Ekonol/PTFE复合材料力学性能和摩擦学性能的研究［J］.润滑与密封，2008，33（6）：6.

［14］Kumlutas D.A Numerical and Experimental Study on Thermal Conductivity of Particle Filled Polymer Composites［J］.Journal of Thermoplastic Composite Materials，2006，19（4）：441-455.

［15］王玉莉.自润滑活塞环导热特性研究及其设计制备［D］. 2013，5：38-40.

Research on the Heat Conduction of the Self-lubricating Piston Ring

WANG Sai-miao1，ZHENG Su-lu2，WANG Xiang-ping2，MAO Yun-yan2，PENG Xue-yuan1
（1.School of Energy and Power Engineering，Xi′an Jiaotong University，Xi′an 710049，China；2.Hengzhou Testing Center of Quality Technical Supervision，Hengyang 324000，China）

As the self-lubricating piston ring fails to work because of the frictional heat，the thermal conductivity coefficients of twophase filling components are established to calculate the finite element model and the effect of eighteen kinds of filling materials on the thermal conductivity coefficients of the piston ring is studied as well.The study results show that the thermal conductivity coefficient of compound materials is proportional to the contents of the filling materials.The shape of the filling particles and its direction have greater effects on the coefficient，and the bigger the character length of the particles along the heat flow direction，the higher the coefficient of the compound materials is.

self-lubricating piston ring；PTFE；thermal conductivity coefficient

TH45

A

1006-2971（2015）01-0001-06

王赛苗（1991-），女，硕士研究生。E-mail:985119945@qq. com

2014-04-14

国家自然科学基金资助项目（51175407）