基于独立分量分析的六维力传感器标定矩阵的校正

刘宝华，迟鹤翔，李硕果

（1.燕山大学河北省并联机器人与机电系统实验室，河北　秦皇岛　066004；2.北京航空航天大学自动化科学电气工程学院，北京　100191）

基于独立分量分析的六维力传感器标定矩阵的校正

刘宝华1，2，迟鹤翔1，李硕果1

（1.燕山大学河北省并联机器人与机电系统实验室，河北秦皇岛066004；2.北京航空航天大学自动化科学电气工程学院，北京100191）

为了提高六维力传感器的测量精度，提出了一种基于独立分量分析（ICA）的静态标定方法。作用在上平台的各维力经过六维力传感器后形成混合信号，该方法先对混合信号进行ICA分解，即将其分离成独立的分量，再结合理想源信号恢复出各维真实作用力的排序和幅值，最后得出校正后的标定矩阵。仿真结果表明，校正后的标定矩阵更接近标准的标定矩阵，从而提高了六维力传感器的测量精度。

计量学；六维力传感器；独立分量分析；不确定性消除；标定矩阵校正

1　引言

六维力传感器能够同时测量3个力分量和3个力矩分量，可用来监测方向和大小不断变化的力、加速度等物理量。随着应用研究的不断深入，六维力传感器已广泛用于机器人、汽车制造、生物力学、航空航天等领域［1～4］。研究简单、可靠、精度高的传感器标定方法和标定装置对于传感器的研制、生产和使用是必不可少的。在此之前，人们研究了不同形式的六维力传感器的静态标定及解耦［5～9］，获得了较好的测量精度。六维力传感器的标定过程是各维单独加载，理想情况下，某时刻只存在某一维加载力（理想加载力）。但是由于标定装置存在误差，如作用力方向和位置的误差［10］，使得在加载某维力时，在其它维上也加载了力（为附加力）。这些附加力使得加载不准确，且这些附加力和理想加载力通过六维力传感器时会出现维间耦合，使得标定矩阵出现偏差，降低了六维传感器的测量精度。针对该种情况，本文利用独立分量分离原理，根据测量信号和理想源信号还原出真实的加载力，从而使标定矩阵更接近真实值。

2　独立分量分析原理

独立分量分析的基本模型（不含噪声）可以由下式表示，假设x1，…，xn，是观察到的n个随机变量，这些变量是由另外n个随机变量s1，…，sn线性组合得到的：

其中aij为混合系数。将式（1）中的求和表达式用向量-矩阵形式可表示为：

式中：X=［x1，…，xn］T，S=［s1，…，sn］T，A为由混合系数aij组成的n×n的方阵。在模型中，ain和si均未知，所以只有通过已知的观察信号X将A和S同时估计出来。因此，希望找到一个分离矩阵W= A-1将源信号从混合信号中分离出来：

式中Y=［y1，y2，…yn］T，若P为单位矩阵，则分离出的信号Y与源信号完全相同。但实际上P为一广义排列阵，使得Y在幅值和排序上存在不确定性。为了保证ICA模型被估计出来，必须做以下假设：

（1）假定源信号统计独立

这是ICA能够被解出的前提条件，而且这个假设在许多领域得到应用。

（2）独立成分应具有非高斯分布

根据中心极限定理，即独立的随机变量之和的分布趋向于高斯分布。因此，混合信号比独立成分具有更强的高斯性，在分离过程中，可通过对分离结果的非高斯性度量来表示分离结果间的相互独立性，当非高斯性度量达到最大时，则表明已完成对各独立分量的分离。

独立分量分析算法有多种，分为在线算法和批处理算法。标定过程中的数据处理符合批处理算法的模型，在本研究中采用FastICA算法［11］。此算法是批处理中一种计算收敛速度快、信号分离效果好的算法。

3　排序和幅值不确定性的消除

3.1ICA不确定性的表现

将一个排列矩阵及其逆代入式（2），得到X= AS=（AP-1）（PS）。式中PS矩阵中的元素仍然是原来独立变量sj，但是顺序发生了变化。而矩阵AP-1则是另一个新的需要通过ICA算法求解的混合矩阵。因此分离出来的估计信号并不一定与混合前源信号的排序一致。

对源分量S的某一分量和相应的混合矩阵A乘以一个比例因子d并不会对观测值X产生影响，即

因此，分离信号与原始信号之间可能存在幅值的差异，而且这种差异是不能预测的。

3.2排序不确定性的消除两个向量m，n的相关系数矩阵表达式为：

其中C为m，n的协方差矩阵。若m，n越相似，则两者之间的相关系数矩阵的行列式|R|就越小，当m，n相同时，|R|为0。因此2个向量越相似，|R|越趋向于零［12］。

由于在标定过程中，六维力传感器的每维力都是单独加载，所以各维理想加载力的矩阵可以表示为：

式中sii=（ai1，ai2，…，ain），i=1，2，…，6，n为每维力所加载次数（假设每维作用次数均为n）。

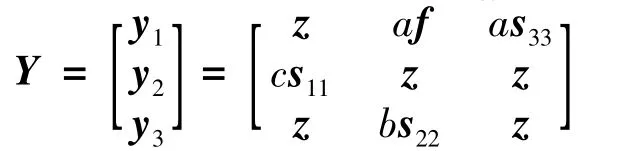
计算分离信号Y中yi与S中各向量的相关系数，若其中yi与sj的相关系数的行列式最小，则yi应排在Y中的第j行，消除了排序的不确定性。

3.3幅值的不确定性消除在使yi与sj对应排列后，就可以对分离信号yi进行幅值的恢复。yi相对于sj的缩放倍数为：

式中pji为式（3）P中的元素。将s3和含有f的向量y1代入式（7）得：

可以看出式（8）中2个向量之间的缩放倍数与af无关。所以只要估计出了as33的缩放倍数，未知量af值也得到了恢复。然后再用1/p31乘以y1得到估计向量：s″3=y1/p31=［zfs33］，这样，未知量f的幅值就被准确恢复出来了。然后根据恢复出的信号计算标定矩阵C得［5］：

式中S″为校正后的源信号。

4　仿真验证

4.1模型的建立

利用三维软件SolidWorks建立了基于Stewart平台的6/3-3型六维力传感器模型［13］，这种形式的六维力传感器具有力的各向同性性质。其结构由上平台、下平台、六根弹性体组成，如图1所示。上平台的6个球铰中心在同一个圆周上，下平台的6个球铰分为2组，一组中的3个球铰中心在一个圆周上，另一组的在另一个圆周上。弹性体材料设为铝合金H12，上下平台材料设为45钢。建模时以过上平台平面中心点的两条相互垂直的直线为X，Y轴所在位置，以上、下平台2个中心点连线为Z轴所在位置，且指向下平台方向为正。为了节省计算所需机时和对内存的需求，上下平台对精度计算要求不高，所以定义上下平台的网格间距较宽，设为100 mm；弹性体部分对精度要求比较高，所以弹性体的网格间距较小，设为20 mm。模型的有限元网格划分如图2所示。球铰接处定义了接触对，理论计算中，由于球铰接是表面光滑的球面副，因此设定为无摩擦接触，这样就可以模拟理想情况的无摩擦球铰接。在实际测量中，球铰接处确实存在摩擦，但在铰接处加润滑脂后，摩擦力的影响很小，即连杆主要受拉压力作用［14］。

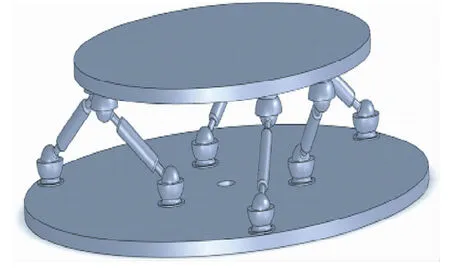
图1　6/3-3型六维力传感器三维模型

图2　传感器在COSMOS中划分网格

4.2标定矩阵的校正

4.2.1理想加载

上平台各维力按幅值范围是-100～100 N，步长Δ=10 N，力矩-100～100 N·m，步长Δ=10 N·m依次进行加载，加载力S各维波形如图3。

从弹性体中读取混合信号X，根据式（9）求得标准标定矩阵为

图3　各维加载力波形

4.2.2存在附加力时的加载及标定矩阵的校正

如果在加载过程中存在附加力，附加力见表1。

表1　存在附加力的情况

由于存在附加力，从各弹性杆中读取的各弹性杆受力数据X′波形如图4所示。

若此时忽略附加力的存在，即仍用理想加载力S计算标定矩阵C′，则根据式（9）有：

经过ICA处理后得到各维加载力的波形如图5所示，从图5可见，理想加载力和附加力（在图中用圆形标出）的波形被估计出来了，但它们在排序和幅值上都发生了变化。利用本文提出的消除排序和幅值不确定性的方法，恢复出各附加力的幅值，得到了校正后各维力S″的波形如图6所示。

图4　存在附加力时从各弹性体中读取的混合信号波形

图5　经过ICA后得到各维加载力的波形

在此基础上用S″代替理想加载力S，根据式（9）求得校正后的标定矩阵：

4.2.3标定矩阵对比分析

为了比较忽略的附加力和考虑附加力两种情况下标定矩阵与标准标定矩阵的接近程度，将C′与标准标定矩阵C的逆相乘得P1：

P1对角线上元素远大于非对角线上元素，且对角线上元素接近于1，因此P1接近单位矩阵。为了量化矩阵接近单位阵的程度，采用了2个指标，用串音δECT来判断矩阵接近排列阵的程度［15］：

式中：pij为P1中第i行j列元素，maxkpik表示P1中第i行各列中最大值，N=6。δECT越小，则P越接近排列阵。经计算P1的串音δECT1=0.598 6。然后判断对角线上元素与1的误差和：

式中pii为P1中对角线上元素。经计算，P1对角线上元素与1的误差和Er1=0.080 2。

图6　不确定性消除后的各维力波形

将校正后的矩阵C″与标准标定矩阵C的逆相乘得P2：

根据式（11）、式（12）求得P2的串音δECT2=0.018 7，P2对角线上元素与1的误差和Er2=0.001 8。2种情况的结果对比如表2所示。

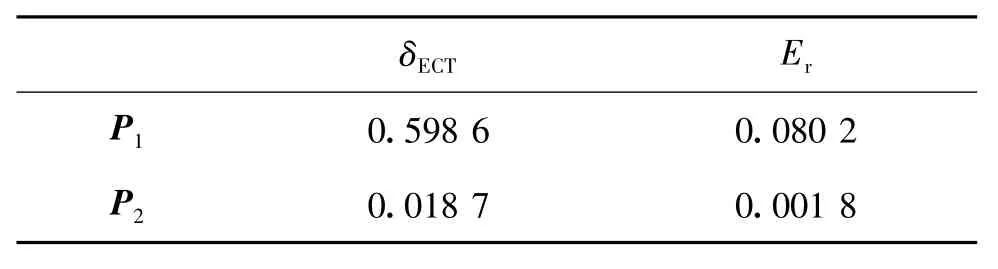
表2　两种情况的结果对比

可见P2的δECT与Er较P1的小，说明P2更接近单位阵，即校正后的标定矩阵C′′更接近标准标定矩阵C。

5　结论

在六维力传感器静态标定过程中，由于标定装置制造不精确或人为操作错误，会使加载力的大小和方向发生改变，从而使弹性体输出的信号也发生改变，但这些改变是未知的，因此在计算标定矩阵时，会产生误差。独立分量分析是可以将相互独立的信号分离，因此可以通过适当构造源信号，将六维力传感器的各维信号分离。本文通过结合源信号，对分离结果进行排序及幅值的校正，恢复出了理想作用力外的附加作用力，并且可以根据恢复出的信号进行标定矩阵的校正，从而提高了六维力传感器静态标定的精度。

［1］姚智慧，张付祥.机器人六维力传感器研究概况及发展预测［J］.广东自动化与信息工程，2002，（3）：7-9.

［2］宋国民，张为公，秦文虎，等.基于车轮力传感器的汽车制动测试系统开发及应用［J］.测控技术，2001，20 （7）：7-9.

［3］张美芹，王人成，胡晓.六分量应变式力传感器弹性体［J］.中国康复医学杂志，2005，20（10）：768-769.

［4］高理富，宋宁，葛运建，等.航天机器人用六维腕力传感器动态特性研究［J］.机器人，2002，24（4）：319-323.

［5］许德章，吴仲城，葛运建，等.机器人六维腕力传感器耦合矩阵的确定与摄动分析［J］.仪器仪表学报，2005，26（1）：78-79.

［6］金振林，岳义.Stewart型六维力传感器的静态解耦实验［J］.仪器仪表学报，2006，27（12）：1715-1717.

［7］张景柱，郭凯，徐诚.六维力传感器静态解耦算法应用研究［J］.传感器与微系统，2007，26（12）：58-59.

［8］姜力，刘宏，蔡鹤皋.多维力/力矩传感器静态解耦的研究［J］.仪器仪表学报，2004，25（3）：284-287.

［9］石中盘，赵铁石，厉敏，等.大量程柔性铰六维力传感器静态解耦的研究［J］.仪器仪表学报，2012，33（5）：1062-1069.

［10］刘正士.机器人六分量腕力传感器加载试验台系统误差分析［J］.计量学报，1998，19（1）：44-49.

［11］Hyvärinen A.Fast and robust fixed-point algorithms for independent component analysis［J］.IEEE Trans on Neural Networks，1999，10（3）：626-634.

［12］郭瑜，高艳，郑华文.旋转机械阶比跟踪中的阶比交叠噪声消除［J］.振动与冲击，2008，27（10）：99-100.

［13］姚建涛.大量程预紧式六维力传感器及静态标定研究［J］.仪器仪表学报，2009，30（6）：56-61.

［14］陆永华，赵东标，吕霞，等.Stewart六维力/力矩传感器弹性体的设计分析［J］.南京航空航天大学学报，2005，37（3）：376-378.

［15］CichochiA，UnbehauenR，RummertE.Robust Learning Algorithm for Blind Separation of Signals［J］.Electronics Letters，1994，30（17）：1386-1387.

Correction in Calibration Matrix of Six-axis Force Sensor Based on Independent Component Analysis

LIU Bao-hua1，2，CHI He-xiang1，LI Shuo-guo1
（1.Hebei Provincial Key Lab of Parallel Robot and Mechatronic System，Yanshan University，Qinhuangdao，Hebei 066004，China；2.School of Automation Science and Electrical Engineering，Beihang University，Beijing 100191，China）

To improve the measurement accuracy of the six-dimensional force sensor，a static calibration method based on independent component analysis（ICA）is proposed.Force acting on the platform forms mixed-signal after the sixdimensional force sensor.Firstly，the mixed-signal is decomposed to separate components with ICA.Then combined with the ideal source signal to recover the real sort and amplitude of the dimensional force，and finally came to the corrected calibration matrix.The simulation results show that，the corrected calibration matrix is closer to the standard one，which improves the measurement accuracy of the six-dimensional force sensor.

Metrology；Six-axis force sensor；Independent component analysis；Indeterminacy eliminating；Calibration matrix correcting

TB931

A

1000-1158（2015）01-0067-05

10.3969/j.issn.1000-1158.2015.01.15

2012-07-02；

2013-03-18

刘宝华（1966-），男，山东昌邑人，燕山大学教授，博士，从事计算机应用方向研究。liubaohua@ysu.edu.cn