一类多涡卷系统的混沌同步
2015-10-25李庆宾李亮毛北行
李庆宾,李亮,毛北行
(郑州航空工业管理学院数理系,郑州450015)
一类多涡卷系统的混沌同步
李庆宾,李亮,毛北行
(郑州航空工业管理学院数理系,郑州450015)
研究了一类多涡卷系统的混沌同步和滑模混沌同步问题,并利用Lyapunov稳定性理论得出了驱动系统与其响应系统实现混沌同步和滑模混沌同步的充分条件。计算机模拟仿真的结果说明了结论的正确性。
混沌同步;涡卷系统;稳定性
自驱动-响应同步方法问世以来,人们对混沌控制、混沌同步和它们的应用进行了广泛而深入的研究,并取得了一些有价值的成果[1-6]。陈志伟、高岩波和陆国平[7]研究了Duffing混沌系统基于Terminal滑模控制的投影同步问题,证明了投影误差的稳定性。张昭晗和高金峰[8]研究了参数不确定异结构混沌系统的自适应同步控制问题。刘金桂、黄立宏和孟益民[9]研究了基于主动滑模控制的混沌系统函数的投影同步问题,借助Lyapunov稳定性理论和主动滑模控制方法设计了主动滑模控制器。康宇等[10]研究了不确定多变量线性系统的快速收敛滑模变结构控制问题。邱国英和杨德刚[11]利用自适应反馈方法设计了一个针对终端滑模的优化组合方案,并实现了一类混沌系统的半有限时间稳定。吕恩胜[12]研究了一类n-涡卷Jerk系统的电路设计问题。在此基础上,我们研究了一类多涡卷系统的混沌同步和滑模混沌同步问题,利用Lyapunov稳定性理论得出了驱动系统与其响应系统实现混沌同步和滑模混沌同步的充分条件,并通过计算机模拟仿真验证了结论的正确性。
1 多涡卷系统的混沌同步
设计一类多涡卷混沌系统
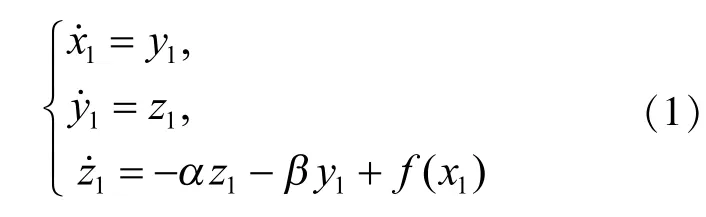
作为驱动系统,其中,x1、y1、z1∈R为系统的状态变量,α、β为系统参数,f(x1)为非线性项。对应的响应系统为

定义驱动系统(1)和响应系统(2)的误差为e1= x2-x1,e2=y2-y1,e3=z2-z1,则相应的误差系统为

2 多涡卷系统的滑模混沌同步
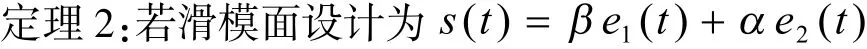


3 数值仿真
下面我们给出一个多涡卷Jerk系统的算例,并通过计算机模拟,验证结论的正确性。
设计驱动系统为




图1 混沌同步的误差曲线
2)当滑模面设计为s(t)=βe1(t)+αe2(t)+e3(t),控制器取u(t)=f(x1)-f(x2)-|ε(s)|sign(s(t))时,驱动系统(4)与响应系统(5)能实现滑模混沌同步,对应的误差曲线如图2所示。
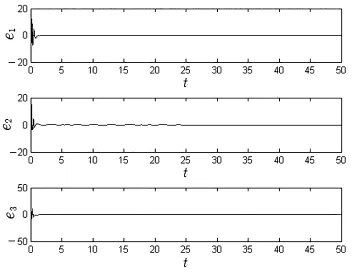
图2 滑模混沌同步的误差曲线
[1]毛北行,崔红新.复杂网络混沌系统的最优控制[J].经济数学,2013(3):22-24.
[2]褚衍东,李红敏,张建刚,等.带有时变时滞和非线性耦合的复杂网络同步[J].安徽大学学报(自然科学版),2012(2):9-14.
[3]毛北行,王东晓.时滞Lurie复杂网络与网络间的混沌同步[J].重庆师范大学学报(自然科学版),2014(6):83-86.
[4]LYUL,LIG,GUOL,etal.GeneralizedChaos Synchronization of a Weighted Complex Network with Different Nodes[J].Chin Phys B,2010,19(8):080507-1.
[5]卞秋香,姚洪兴.复杂网络的线性广义同步[J].系统工程理论与实践,2011(7):1334-1340.
[6]MEIJ,JIANG M H,WANG J.Finite-time Structure IdentificationandSynchronizationof Drive-response Systems with Uncertain Parameter[J].Communications in Nonlinear Science and Numerical Simulation,2013,18(4):999-1015.
[7]陈志伟,高岩波,陆国平.Duffing混沌系统基于Terminal滑模控制的投影同步[J].南通大学学报(自然科学版),2013(1):24-29.
[8]张昭晗,高金峰.参数不确定异结构混沌系统的自适应同步控制[J].郑州大学学报(工学版),2011(6):117-125.
[9]刘金桂,黄立宏,孟益民.基于主动滑模控制的混沌系统函数投影同步[J].经济数学,2011(3):6-8.
[10]康宇,奚宏生,季海波,等.不确定多变量线性系统的快速收敛滑模变结构控制[J].中国科学技术大学学报,2003(6):718-725.
[11]邱国英,杨德刚.基于终端滑模和自适应反馈方法的一类混沌系统稳定性分析[J].重庆师范大学学报(自然科学版),2014(6):92-96.
[12]吕恩胜.一种n-涡卷Jerk系统及其电路设计[J].伊犁师范学院学报(自然科学版),2005(1):51-56.
【责任编辑 王云鹏】
Chaos Synchronization of a Class of Multi-scroll Systems
LI Qingbin,LI Liang,MAO Beixing
(Department of Mathematics and Physics,ZhengzhouInstitute of AeronauticalIndustry Management,Zhengzhou 450015,China)
The problems of chaos synchronization and sliding model chaos synchronization of a class of multi-scroll systems were studied in this paper.The sufficient conditions for drive system and its response system to achieve chaos synchronization and sliding model chaos synchronization were got according to Lyapunov stability theory.The results of computer simulation verified the correctness of the given results.
chaos synchronization;multi-scroll systems;stability
O231.2
A
2095-7726(2015)12-0017-03
2015-08-26
国家自然科学基金数学天元基金(11226337);河南省高等学校重点科研项目(15B110011);河南省科技厅软科学研究计划项目(142400411192)
李庆宾(1982-),女,河南南阳人,讲师,研究方向:混沌同步。
