基于实际水文条件的点目标回波仿真
2015-10-25李永胜吕林夏陈亚林
陈 发,李永胜,赵 罡,吕林夏,陈亚林
(1.中国船舶重工集团公司 第705研究所,陕西 西安,710075;2.水下信息与控制重点实验室,陕西 西安,710075)
基于实际水文条件的点目标回波仿真
陈发1,2,李永胜1,赵罡1,吕林夏1,陈亚林1
(1.中国船舶重工集团公司 第705研究所,陕西 西安,710075;2.水下信息与控制重点实验室,陕西 西安,710075)
为了分析水文条件对主动水声探测系统信号的影响,首先利用射线声学理论和BELLHOP模型,求解实测海洋水文数据下的本征声线,然后选取主要声线所携带的幅度、时延、相位等信息构建点目标回波信号模型。仿真分析给出了发射单频正弦脉冲下的点目标回波仿真波形,并与实测波形进行了对比。计算结果表明,基于水文条件的点目标回波模型可以很好的模拟水文条件对水声信号的影响。
水文条件;目标回波;本征声线
0 引言
主动水声探测系统通过发射信号,接收目标反射回来的信号探测水下目标[1]。由于目标信息包含在回波中,所以通过处理接收信号可以判断目标的存在,利用回波信息还可以测定目标距离、速度、方位、航向等运动要素,但是水声系统的性能会受到海洋环境的影响。水声信道的低信息传输率、色散效应、界面影响、声速剖面、以及多途等特性都会对接收信号产生影响。我国周边海域多为浅海,海洋环境参数复杂多变。为了提高系统的环境适应性,有必要研究海洋信道对主动水声探测信号的影响情况。
水声信道对主动水声探测信号的影响主要体现在2个方面:一是由于信道频散和多途导致的波形衰减;二是参数的时变特性引起波形起伏。这些都会导致接收信号相对发射信号发生波形畸变和模糊,具体表现为幅度起伏、时频扩展、去相关性。信道参数种类多样,其中影响较大的是水文条件,也就是海洋中的声速分布。
近年来,国内外学者开展了海洋环境参数对水声探测系统作用距离的影响研究[2],方法多集中于求解经典声呐方程,对于海洋环境参数多使用平面波混响级RL和传播损失TL代替。由于这2个参数是平均值、经验值,并不能反映信道的空变特性。文中利用海洋实测声速分布数据,结合BELLHOP射线声学模型,计算本征声线[3],然后选取合适的声线信息(幅度、相位和延时),构建点目标回波,采用混合模型仿真混响,并叠加高斯白噪声,从而得到接收信号。通过与实测数据对比分析,验证了模型的正确性和可行性。
1 浅海声传播模型
1.1射线声学
海水介质中的声传播在数学上可以用波动方程的解来描述[4],这个解是在特定问题的相应边界条件和介质条件下得到的。波动方程是声压p对坐标x,y z,和时间t的偏微分方程式中,c为声速,且为坐标的函数,通常考虑为仅与深度有关。

有2种方法求解上述方程,一种是简正波理论,利用名为简正波的特征函数描述声传播,每一个特征函数都是方程的一个解,将这些简正波叠加起来,以满足边界条件和声源条件;另一种是射线声学,利用声线图描述传播图像,声场分布更加形象化。2种方法应用场合不同,前者通常用于低频近场,后者只适用于高频。由于目前的主动水声探测系统使用的频率通常为几十kHz,所以通常使用声线模型来求解探测信号声场。
射线声学的2个基本方程为

式(2)为强度方程,描述声能量随声线传播的情况;式(3)为程函方程,描述声线的走向,该方程不仅可以导出声线的方向,还可以求得声线的轨迹和传播时间。
1.2BELLHOP模型
射线声学模型有很多便于计算机实现的算法,BELLHOP是其中较为常用的,它由Porter和Bucker从地震勘探常用的高斯波束追踪法演变而来[5-6],该算法解决了声影区的问题,特别适合高频、距离相关问题的求解。假设条件为点源在声速仅与深度有关的柱形波导中。
圆柱坐标系下的标准射线方程为

其中:r=r(s),为弧长的函数;c(r,z)为声速。
声线的曲率和宽度由以下辅助方程推导而来

声线定义为

加入初始条件后,可以求得声场
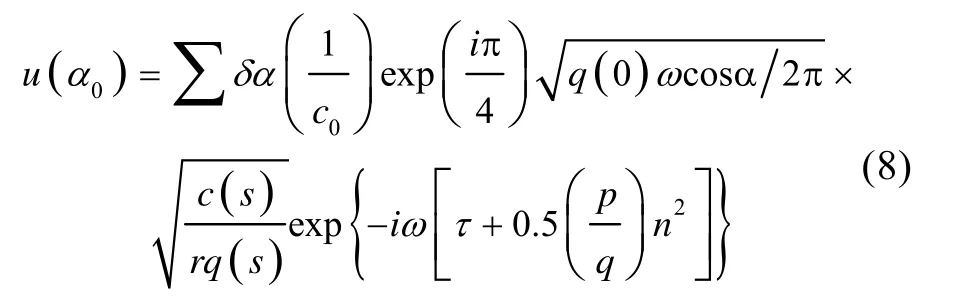
其中,α为掠射角,该式利于计算机实现。输入水文条件(声速剖面、海底特性等)和求解参数,可以使用BELLHOP算法计算得到声线图。本征声线为经过发射点和接收点之间的声线,该算法还可以计算每根本征声线所携带的信息:幅度衰减系数、时延和相位变化量。
2 点目标回波模型
从大多数应用场合来看,水声信道可以看成是缓慢时变的相干多途信道[7]。浅海试验数据已经表明,信道至少在20 s内是稳定的。由于海洋介质中的声速不是恒定的,加上界面的反射效应,声波在海水中的传播是多途的。不同路径到达的信号相互干涉叠加形成接收信号。
声波是微振幅波,满足叠加定理,因此水声信道对信号的影响可以使用线性网络的系统函数来描述。假设声传播过程中不存在色散现象,系统函数可以描述为
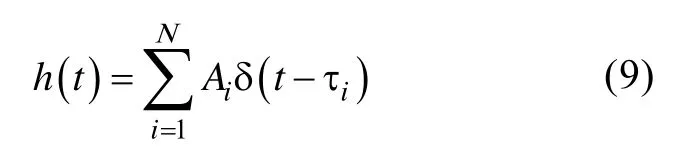
其中多途路径数为N,假设发射信号为s(t),则接收到的回波信号为

利用BELLHOP模型可计算出每根声线的幅度衰减系数、时延和相位偏转,故,式(10)简化为
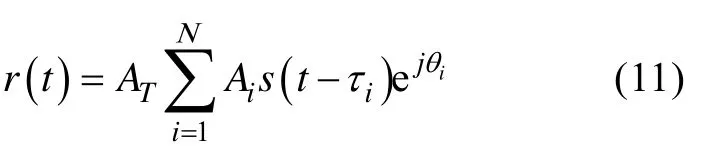
式中:AT为点目标强度;Ai,τi,θi为第i条路径的幅度衰减系数、时延和相位偏移量,其中时延考虑了目标运动的影响。理论上能够到达接收点的声线是无数多的,为了计算的方便和实际情况的需要,可以只计算那些衰减量比较小的声线。
同时到达接收阵列的还有混响和噪声。混响是海洋中散射体的散射成分总和,具体可以划分为体积混响和界面混响。噪声包括海洋环境噪声和系统自噪声。那么接收信号可以表示为

其中:srev(t)为体积混响、海面混响、海底混响之和;snoise(t)为海洋环境噪声。
3 仿真分析
3.1信道参数
这里采用海洋实测声速剖面计算信道参数,海深H=150 m ,其相对海面声速分布如图1所示,可见该海域声速呈负梯度分布。
设计4组仿真试验,其基本参数为声源深度Hs=70 m ,接收深度Hr=65 m ,发射单频脉冲信号中心频率为f0=20 kHz,采样频率fs=128 kHz ,计算波束数Num=101,垂直发射角为φ=±10o。假设海底是平坦的,底质为淤泥粘土,其特性参考理论值[8]:海底声速cs=1535 ms ,海底介质密度ρb=143gcm3。每组试验的探测距离和目标径向速度,如表1所示。
下面给出第1组试验的信道参数计算结果。由于入射声场本征声线较少,下面给出入射时的信道冲击响应(实际上对应的就是每根本征声线所携带的幅度衰减和时延信息)。
系统使用收发合置换能器,因此还需要计算从目标反射回去的本征声线信息,才能构建目标回波。首先利用图2中的信道冲击响应,结合式(11)构建点目标反射波,以此合成信号作为发射信号,交换Hr和Hs,重置垂直发射角为φ=±20o,其他参数不变,求解本征声线,见图3。
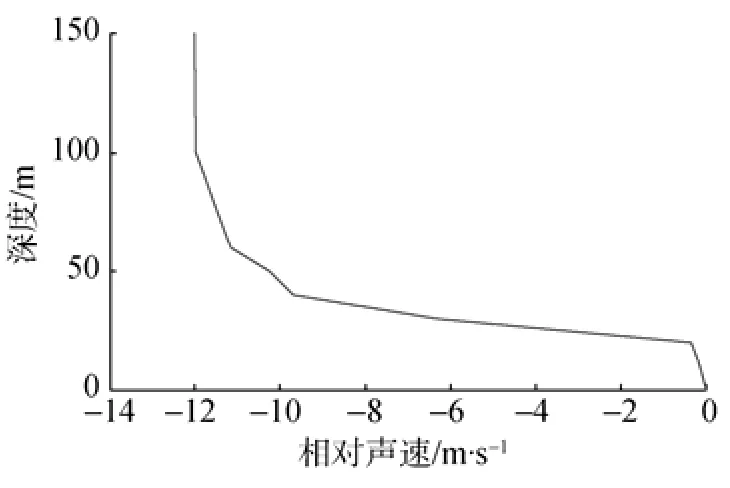
图1 浅海相对声速剖面Fig.1 Profile of relative sound speed in shallow sea
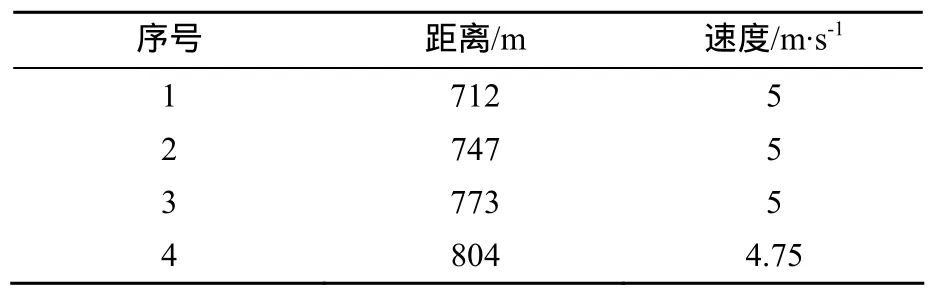
表1 仿真参数Table 1 Parameters of simulation

图2 声源发射信号时的信道冲击响应Fig.2 Impulse response of channel to sound source transmitting signal
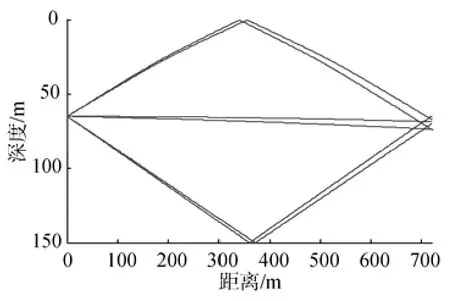
图3 目标反射到接收器的主要声线Fig.3 Main sound ray reflected from target to receiver
从图3可以看出,到达目标的声线除了直达声之外,还有经海面和海底反射的声线,接收信号为不同途径到达信号的叠加。
反射信道冲击响应如图4所示。可见信道冲击响应不仅与信道有关,还和换能器、目标深度、发射角有关。注意:以上信道参数,是在假设信道不存在频散条件下求得的;程序中相位偏转信息已经通过换算到幅度衰减上。根据图2和图4中的信道冲击响应参数,就可以利用模型完成点回波重建。
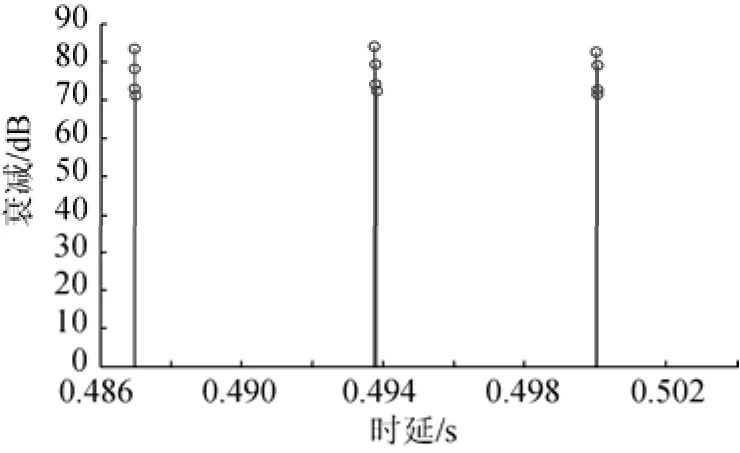
图4 目标反射信号时的信道冲击响应Fig.4 Impulse response of channel when target reflects signal
3.2回波仿真对比分析
下面通过比较发射信号、回波信号的特征,分析信道对信号的影响情况。因为实际海洋环境噪声并非高斯白噪声,浅海声传播会受到海底介质特性的影响,但实际海底介质特性与模型假设相差较大,所以仿真波形与实测波形在细节上存在差异。这里主要考虑信号的脉宽和频域特性,并分析信号的去相关性。海上试验示意见图5。

图5 海上试验环境示意图Fig.5 Schematic of sea trial environment
发射信号为单频矩形脉冲,脉宽T=60 ms(信号持续时间均小于信道时间相关半径,满足模型假设条件)。发射信号如图6所示。
因为水听器实际接收到的信号还包括混响和噪声,且混响为主要干扰。所以为了更好的与实测数据进行对比,还需要进行混响建模仿真。
混响伴随着发射信号而产生,这里采用点散射和单元散射混合模型计算混响,模型假设条件为收发合置声呐位置固定,声波在介质中沿直线传播,忽略二次散射,信号为窄带信号,计算得到的体积、界面混响及总混响如图7所示。可见混响持续时间较长,且随时间衰减很快。
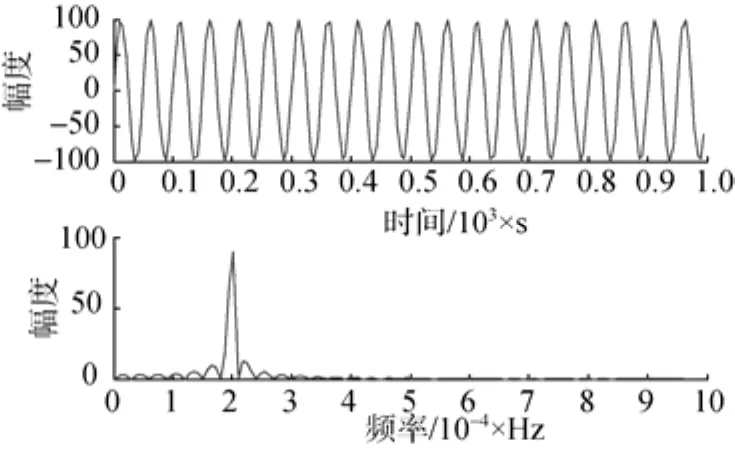
图6 发射矩形脉冲信号时频波形图Fig.6 Time-frequency waveform of transmitting rectangular pulse signal

图7 仿真得到的体积、海面、海底混响及总混响波形Fig.7 Waveforms of volume,sea surface,sea bottom reverberation and total reverberation obtained by simulation
利用信道冲击响应参数和式(11)构建点目标回波,这里考虑了目标的径向运动带来的多普勒频移。将发射回波、混响、噪声叠加起来,得到接收信号。由于发射信号载频较高,且为窄带特性,为了减少系统硬件和软件的复杂性,可对信号的复包络进行采样。这里对信号先进行正交解调[9],然后对2个正交分量进行采样,采样率为fs′=4 kHz,从而减少了数据量,得到的目标回波见图8(这里只给出了第1组试验的结果图,其余组均只给出了分析结果)。为方便后面与实测回波进行对比,图8中的时域波形只给出了目标反射回波部分;信号频谱主要由回波和混响组成,且回波相对混响有频移,频移量约等于多普勒。
海上试验接收到的信号时频分布参见图9。为了观察的方便和对比的需要,图中的时域图只给出了目标回波出现的区间。从实测接收波形的频谱可以看出,混响与回波的中心频率之差基本上等于目标的多普勒,偏差来源于散射体、换能器的运动。实测与仿真混响频谱相差较大,这是因为海底介质特性采用了理论值,所以海底混响与仿真存在差异。对比实测波形和仿真回波,两者在细节上存在较大差别,下面从回波脉宽、带宽、中心频率、互相关系数等参数进行研究。
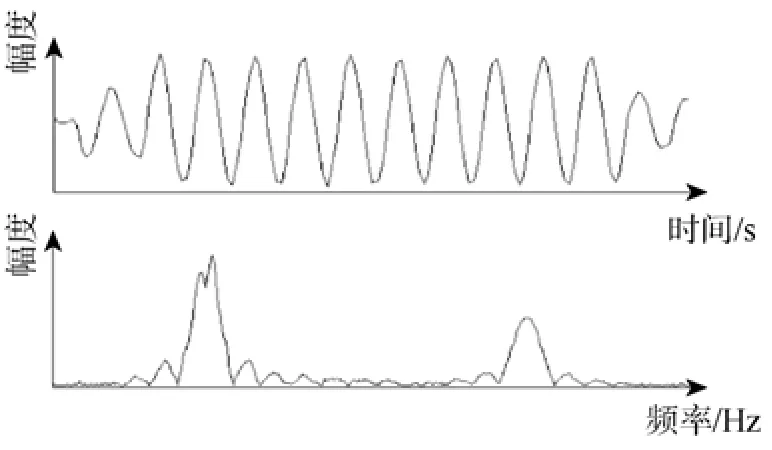
图8 仿真正交采样回波时频波形Fig.8 Simulated time-frequency waveform of orthogonal sample echo

图9 实测正交采样回波时频波形Fig.9 Measured time-frequence waveform of orthogonal sample echo
实测和仿真回波参数相对误差计算结果如表2所示。表中的频率为正交采样后的频谱中心频率,带宽定义为峰值左右第1个零点之间的差值;求解发射信号与仿真回波之间互相关系数的积分时间为回波持续时间。从表2可以看出,信道对信号进行了去相关,这会影响信号的相关检测性能。

表2 仿真与实测回波误差分析Table 2 Error analysis between simulated and measured echoes
从表2可以看出,仿真得到的回波信号频率误差较小,而带宽和脉宽误差在15%以内,误差来自海底散射体的影响。利用水文条件构建的点目标回波模型,能够很好地反映声信道对发射信号的变换:幅度相位起伏、时域频域扩展、去相关等。脉宽和带宽计算结果表明,利用该模型来反映信道特性是可行的,该模型可以比较准确地反映信道特性。
4 结束语
为了探索水文条件对水声探测系统信号的影响,文中采用实测浅海声速数据,利用BELLHOP模型计算本征声线,然后利用主要声线信息重建点目标回波。将其与混响、噪声叠加起来就得到水听器的接收信号。
仿真结果表明,虽然海底、噪声、混响等特性与仿真模型有较大差异,但通过分析信道对信号主要的影响因子,结果表明,该模型可以很好地反映信道特性。同时与实测波形的对比、计算结果验证了该模型的可行性。基于水文条件的点目标回波模型理论简单,容易实现,可为今后进一步研究水文条件对水声探测系统检测性能的影响打下基础。
[1]田坦,刘国枝,孙大军.声纳技术[M].哈尔滨:哈尔滨工程大学出版社,2006.
[2]何心怡,钱东,王光宇,等.水文条件对鱼雷声自导作用距离的影响[J].鱼雷技术,2007,15(5):33-36.
[3]李永平,毛卫宁.基于分层海洋射线传播模型的接收信号仿真[J].声学与电子工程,2003(1):12-15.
[4]Urick R J.水声原理[M].洪申,译.哈尔滨:哈尔滨船舶工程学院出版社,1990.
[5]Alec J Duncan,Amos L Maggi.A Consistent,User Friendly Interface for Running a Variety of Underwater Acoustic Propagation Codes[J].Proceeding of Acoustic,2006,20(22):471-487.
[6]Poter M B,Bucker H P.Gaussian Beam Tracing for Computing Ocean Acoustic Fields[J].The Journal of the Acoustical Society of America,1987,82(4):1349-1359.
[7]惠俊英,生雪莉.水下声信道[M].北京:国防工业出版社,2007.
[8]刘伯胜,雷家煜.水声学原理[M].哈尔滨:哈尔滨工程大学,2010.
[9]潘仲明.随机信号分析与最优估计理论[M].长沙:国防科技大学出版社,2007.
(责任编辑:许妍)
Simulation of Point Target Echo Based on the Actual
Hydrological Conditions
CHEN Fa1,2,LI Yong-sheng1,ZHAO Gang1,LÜ Lin-xia1,CHEN Ya-lin1
(1.The 705th Research Institute,China Shipbuilding Industry Corporation,Xi′an 710075,China;2.Science and Technology on Underwater Information and Control Laboratory,Xi′an 710075,China)
To analyze the influences of hydrological conditions on the signal of an active hydroacoustic detection system,the ray acoustic theory and BELLHOP models are employed to solve the eigenray from measured oceanic hydrological data.A point target echo model is built with the information of amplitude,time-delay,and phase,which are carried by the main eigenray.The point target echo waveform is obtained from numerical simulation in the case of transmitting single-frequency sine impulse,and is compared with the measured waveform.Computational results show that the point target echo model based on hydrological conditions is applicable to simulate the influences of hydrological conditions on underwater sound signal.
hydrological conditions;target echo;eigenray
TJ630.34;TN911
A
1673-1948(2015)04-0311-05
2015-05-25;
2015-06-03.
陈发(1988-),男,在读硕士,研究方向为水声信号处理.
