基于Multism软件实现一个三维混沌系统的电路设计与保密通讯

马大柱，龙志超，朱 瑜

（湖北民族学院理学院，湖北　恩施　445000）

基于Multism软件实现一个三维混沌系统的电路设计与保密通讯

马大柱，龙志超，朱 瑜

（湖北民族学院理学院，湖北恩施445000）

基于Multism软件设计了一个三维混沌系统的模拟电路，仿真结果与数值模拟结果一致.给出了混沌信号的加密和解密过程，设计了该系统的保密通讯电路.

Multism软件；混沌电路；保密通讯

混沌电路是混沌理论在实际工程的应用.目前研究工作主要体现在两个方面，一是讨论混沌控制与混沌同步的方法［1-2］，二是关注混沌电路在保密通讯方面的应用［3-4］.研究人员不仅提出了Chen系统［5］、Lü系统［6］和Liu系统［7］等整数阶混沌电路，还给出了一系列分数阶混沌电路，如Chua系统［8］、分数阶Rössler系统［9］和分数阶Rössler超混沌系统［10］等.

Multism软件具有强大仿真分析能力，电路可以根据图形和电路硬件描述语言两种输入方式实现，而且可供选择的电子元器件非常丰富.其已成为科研教学中必不可少的软件之一.本文利用Multism软件设计了一个三维混沌系统的模拟电路，数值模拟用于检验模拟电路的仿真结果.设计模块化电路实现对该系统的混沌特性进行研究，从物理意义上说明混沌的存在性.并将混沌特征应用于安全密码通讯，模拟了混沌信号的加密和解密过程.

1　数学模型

一个双翅膀数学模型［4］为：

取a=0.75，b=0.45，计算系统的快速李雅普诺夫指数，如图1所示，两邻近轨道呈指数式增长，表明系统混沌.

2　数值模拟

利用Matlab软件实现式（1）的数值模拟，初值取为x0=0.5，y0=0.1，z0=2，四阶龙格库塔法为数值工具.系统相空间结构如图2所示.图中任意两平面均给出了双涡卷结构，表明该系统为混沌系统.

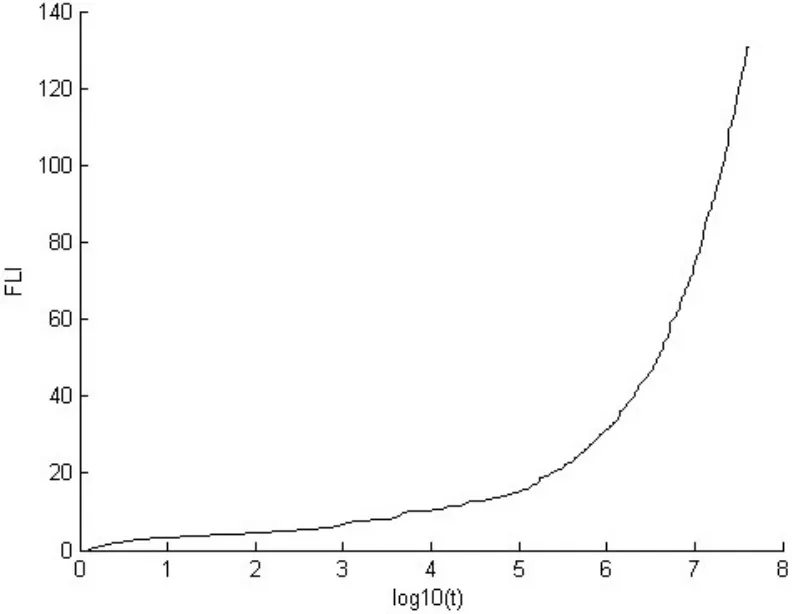
图1　系统快速李雅普诺夫指数Fig.1 Fast Lyapunov exponent of the system

图2　数值模拟图，从左至右依次为x-y、x-z和y-z平面Fig.2 Numerical simulation result，from left to right it refers to x-y，x-z，and y-z，respectively

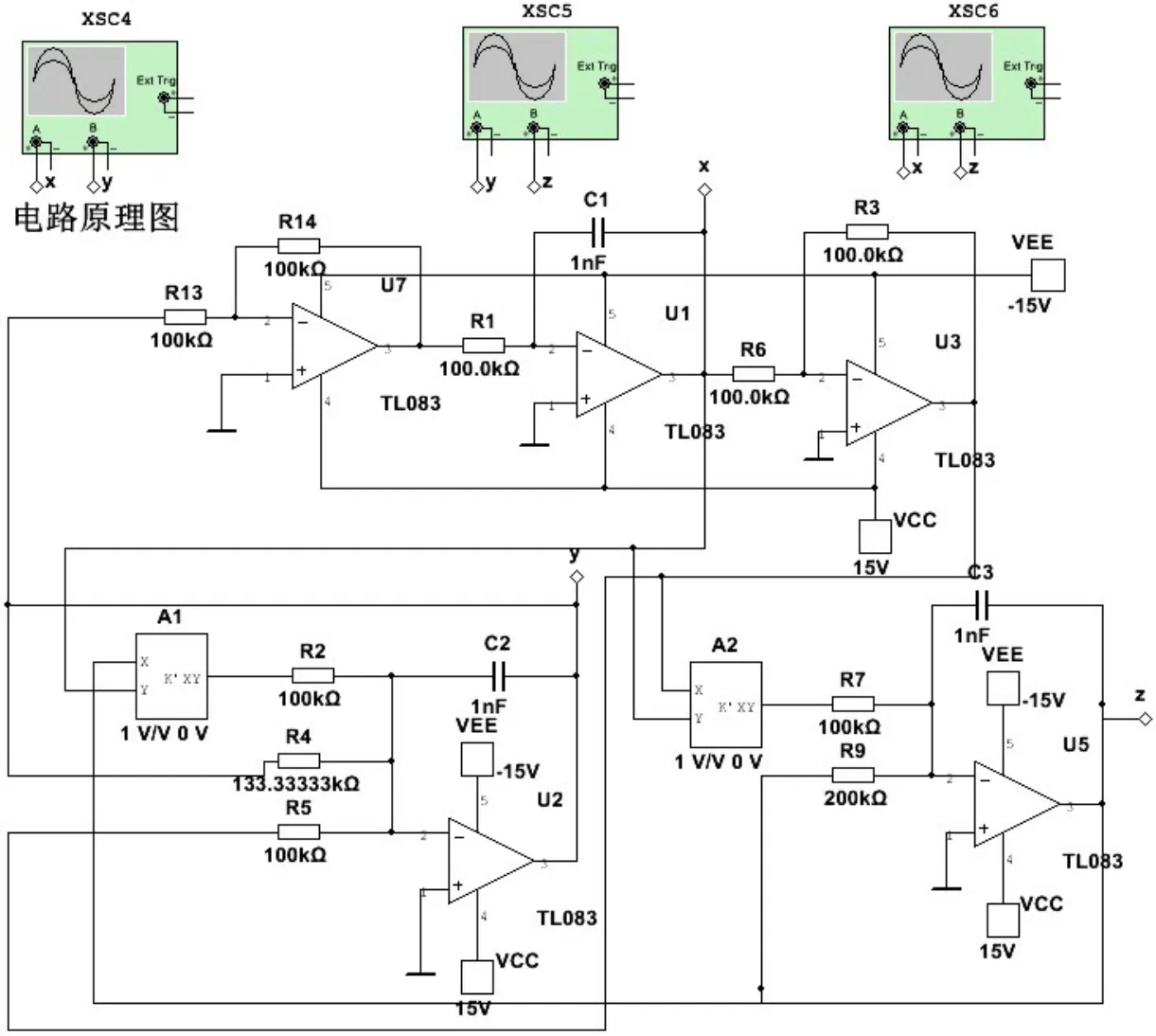
图3　混沌电路图Fig.3 Chaotic circuit diagram

3　混沌电路设计

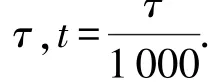
模拟电路中含有运算放大器、电阻器、乘法器和电容4种电子器件.该系统的混沌电路如图3所示，各元器件的参数已在电路图中给出.基于基尔霍夫定律、欧姆定律、虚拟短路、虚拟断路和反向积分电路等原理，可得到关于电压的一阶微分方程组，

令x=U1，y=U2，z=U3，对比式（2）和式（3），可得：

图3即为利用改进型模块化设计方法给出的该混沌系统的模拟电路图.这里电容分别为C1=C2=C3=10 nF，电阻值分别为：R4=133.33KΩ，R9=200KΩ，其余均为100KΩ.三个示波器可观测到对应系统的三个相空间平面.电路仿真结果如图4所示，分别对应于数值模拟图2，两者完全一致.一方面说明电路设计正确，另一方面从物理上说明了该系统确实为混沌系统.

图4　电路仿真图，从左至右依次为x-y、x-z和y-z平面Fig.4 Circuit simulation result，from left to right it refers to x-y，x-z，and y-z，respectively

4　保密通讯电路设计

4.1混沌同步

混沌同步是实现保密通讯的基础.目前已发展了多种混沌同步的方法.本文采用一种普遍使用的方法：反馈型驱动响应式同步.该方法的特点是两个系统存在着驱动与响应的关系，同步可以使得失步后仍然能够重新同步，其已被广泛应用于模拟电路设计、DSP和FPGA等领域.

驱动系统用x作为驱动信号，则有：

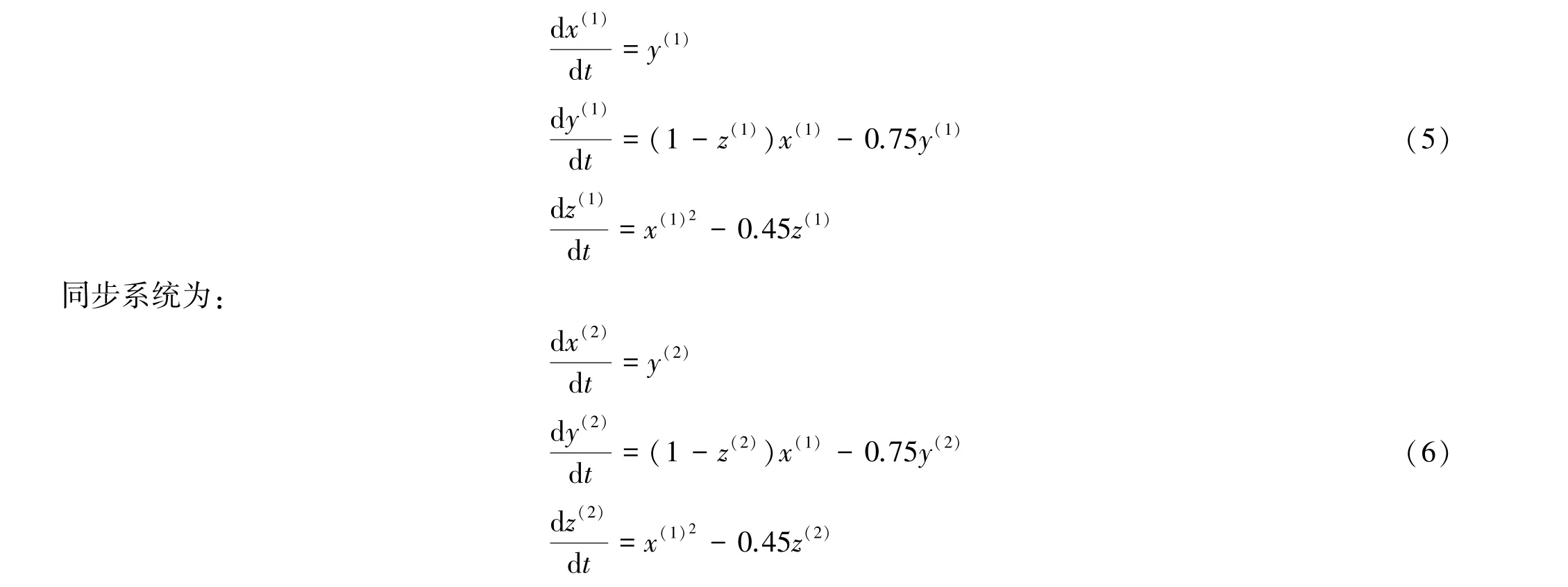
同步的仿真结果如图5所示，误差很快达到0，说明系统快速达到混沌同步.

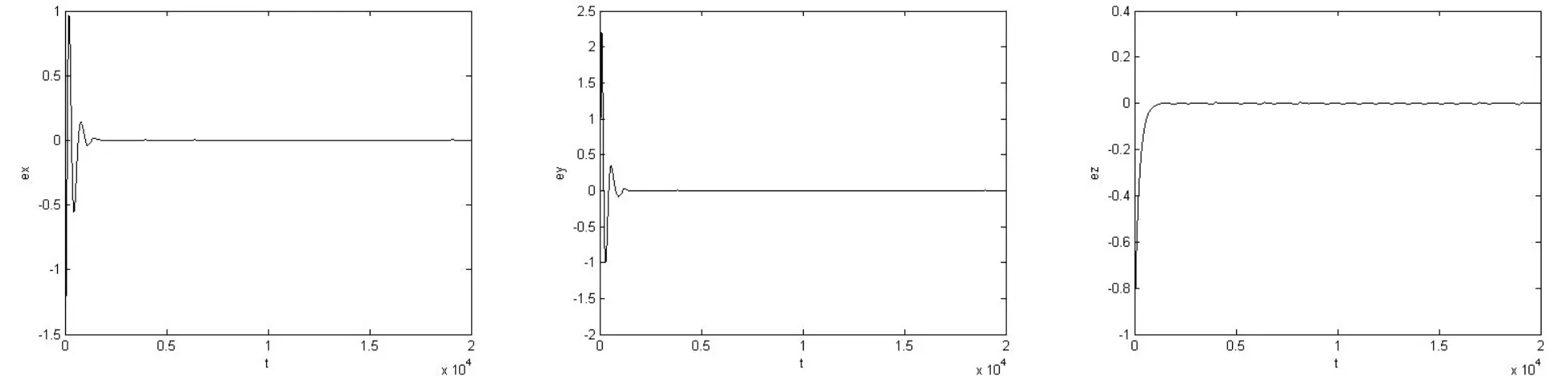
图5　混沌同步图Fig.5 Chaos synchronization

4.2系统加密和解密过程

本文采用混沌掩盖法实现加密和解密过程，即将有用信息掩盖在混沌信号中.在发送端有用信号s和混沌信号y（1）相加，使得通过公共信道的是类似噪声的包含有用信号和混沌信号的叠加信号Sin（Sin=y（1）+s），达到了保密通讯目的.在接受端响应系统和驱动系统实现混沌同步，只需将Sin与同步信号中的y（2）相减就可以还原出有用信号s（Sout=Sin-y（2））.系统保密通讯电路在图6和图7中给出.图6包含了混沌同步和系统的加密解密过程，图7只是子系统-驱动系统.

仿真时初始信号为正弦波形式，驱动系统和同步系统初值任取.电压随时间变化情况如图8所示，从上到下依次为加密前、加密后和解密后效果图，对比发现解密信号与原有信号完全一致.

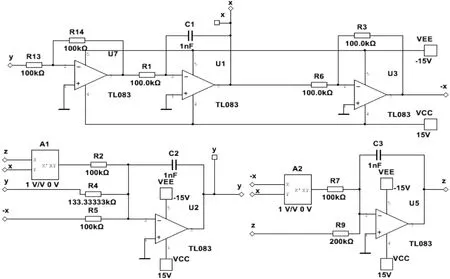
图7　保密通讯电路子图-驱动系统Fig.7 The sub-graph ofsecure communication，it is for the drive system

5　结论

本文基于Multsim软件实现了一个双涡卷混沌系统的模块化电路设计.数值模拟结果与电路仿真结果一致，从本质上说明了系统的混沌特征.并利用反馈型驱动-响应式同步和混沌掩盖法模拟了该混沌系统的保密通讯过程.

［1］HÜBER A.Adaptive Control of Chaotic Systems with Uncertainties［J］.International Journal of Bifurcation&Chaos，1998，8（10）：2041-2046.

［2］GREBOGI C，OTT E.Communicating with chaos［J］.Phys Rev Lett，1993，70（20）：3031-3034.

［3］PECORA L M，CARROLL T L.Synchronization in chaotic systems［J］.Physical review letters，1990，64（8）：821-824.

［4］余思敏.混沌系统与混沌电路原理设计及其在通讯中的应用［M］.西安：西安电子科技大学出版社，2011.

［5］CHEN G，UETA T.Yet another chaotic attractor［J］.International Journal of Bifurcation and Chaos，1999，9（7）：1465-1466.

［6］Xiang-Rong C，Chong-Xin L，Fa-Qiang W，et al.Study on the fractional-order Liu chaotic system with circuit experiment and its control［J］.Acta Physica Sinica，2008，57（3）：1416-1422.

［7］XU Zhe，LIU Chongxin.Realization of fractional-order Liu chaotic system by a new circuit unit［J］.Chin Phys B，2008，17（11）：4033-4038.

［8］LU J G.Synchronization of a class of fractional-order chaotic systems via a scalar transmitted signal［J］.Chaos，Solitons& Fractals，2006，27（2）：519-525.

［9］WANG B，GUAN Z H.Chaos synchronization in general complex dynamical networks with coupling delays［J］.Nonlinear Analysis Real World Applications，2010，11（3）：1925-1932.

［10］LI C，CHEN G.Chaos and hyperchaos in the fractional-order Rössler equations［J］.Physica A：Statistical Mechanics and its Applications，2004，341（1/4）：55-61.

责任编辑：时 凌

A 3D Chaotic System with Its Circuit Implementation and Secure Communication Based on Multism Software

MA Dazhu，LONG Zhichao，ZHU Yu
（School of Science，Hubei University for Nationalities，Enshi 445000，China）

The analogous circuit of a 3D chaotic system is realized based on Multism software.The simulation results are in agreement with the numerical simulation results.The encryption and decryption process of the chaotic signal is given too，and the secure communication circuit of the system is designed.

Multism software；chaotic circuit；secure communication

0317+.2

A

1008-8423（2015）04-0361-04DOI：10.13501/j.cnki.42-1569/n.2015.12.001

2015-11-07.

国家自然科学基金项目（11263003）；湖北民族学院教研项目（2014JY030）；国家民委2015年度教改项目（15067）.

马大柱（1983-），男，博士生，讲师，主要从事数值计算方法和非线性动力学研究.