一种自适应Morlet小波包络解调的弱故障检测方法

牛 超，侯新国，杨忠林

（海军工程大学电气工程学院，武汉 430033）

一种自适应Morlet小波包络解调的弱故障检测方法

牛 超，侯新国，杨忠林

（海军工程大学电气工程学院，武汉 430033）

为自适应实现Morlet小波与故障冲击特征成分的最优匹配，采用基于Shannon小波熵的方法优化带宽参数设计了最优Morlet小波。针对最佳尺度的求取难题，利用谱峭度与小波熵均能敏感反映冲击性的特性，提出了基于峭熵比的最佳尺度的求取方法。基于此，提出基于自适应Morlet小波包络解调的弱故障特征提取方法。仿真实验与实例分析表明：该方法克服了传统包络解调需要人为设定带通滤波器参数的不足，减少人工干预，能自动有效地从强噪背景中提取微弱故障特征，具有一定的工程应用价值。

Morlet小波 自适应包络解调 shannon小波熵 谱峭度 峭熵比

0　引言

包络解调法是电机轴承故障诊断中最常使用的方法之一［1］。在对故障振动信号进行包络解调前，通常要对故障振动信号进行带通滤波。然而，带通滤波的实现需要人为选择滤波中心频率与带宽，应用极为不便［2］。将小波应用于振动信号的包络解调分析是一种常用方法［3］。Morlet小波是在故障诊断领域内常用的一种小波函数，这不仅由于Morlet小波是左右两边都按指数衰减的余弦信号，可以与故障振动信号实现较好的匹配，而且Morlet小波具有非常好的带通滤波特性［4-5］。文献［6］提出基于Morlet小波的包络检波算法提取淹没在噪声中的故障冲击成分和冲击成分所在频带，取得一定效果，但该方法没有考虑Morlet小波的优化，不能自适应实现对冲击成分的最优匹配，影响了包络解调效果。利用最小Shannon小波熵自适应优化带宽参数设计与冲击特征成分相匹配的Morlet小波，将含有被调制信号的信息最丰富的所在频段从原信号频带中分离出来，是优化小波变换算法的一种新思路，但最佳变换尺度的求取是基于Morlet小波分析的难点。文献［4］［7］采用小波变换系数矩阵的奇异值比谱（SingularValue Ratio，sVR）求取最佳尺度，该方法在利用SVR探测信号的周期分量时，存在截断误差导致其经常失效。由于谱峭度和Shannon小波熵均能反映强噪声背景下冲击信号的特征，本文提出基于谱峭度与Shannon小波熵比值即峭熵比（Kurtosis Entropy Ratio， KER）的方法求取最佳变换尺度，以弥补最佳尺度求取方法的缺陷。在此基础上，提出基于自适应Morlet小波包络解调的弱故障特征提取方法，以有效提取强噪声背景下的微弱故障特征。该方法首先依据信号的特点自适应地设计最优Morlet小波，并利用最优Morlet连续小波变换对信号进行全频段带通滤波；然后依据峭熵比自适应地获取最优频带；最后对最优频带小波系数取实部，并对其求模，即可获得最优频带的包络实现包络解调。仿真实验分析表明：该方法克服了传统包络解调需要人为设定带通滤波器参数的不足，能有效地从强噪背景中提取弱故障特征。

1　Morlet小波及其包络解调原理分析

Morlet小波是高斯包络下的复指数函数，其通常的定义式为：

其频谱为：

式中fc是小波的中心频率；fb是带宽参数，决定了波形振荡衰减的快慢程度和母小波的带宽，fb越小，波形衰减得越快，带宽越宽，直至逼近一个脉冲信号；fb越大，则波形衰减得越慢，带宽越窄，最后退化成一个余弦信号。因此，在应用Morlet小波进行故障诊断时，需要优化fb，以实现小波与冲击特征成分的最优匹配。

由式（2），经傅里叶逆变换知小波ψ（t）的实部ψr（t）和虚部ψi（t）分别是t的实偶函数与实奇函数，因此它们的频谱ψr（f）和ψi（f）分别是实偶函数和纯虚奇函数；由于Morlet小波频谱函数仅含有正频率部分，故Morlet小波是解析小波，于是可推知ψr（f）和ψi（f）满足下列关系：

式中sgn（f）为符号函数。上式是一个时间函数Hilbert变换式的等价频域表示，即式（3）表明ψi（t）是ψr（t）的Hilbert变换。

由式（5）知，Wxr（a， b）本质是信号x（ t）通过一个频率响应为Ψr（aω ）滤波器输出。

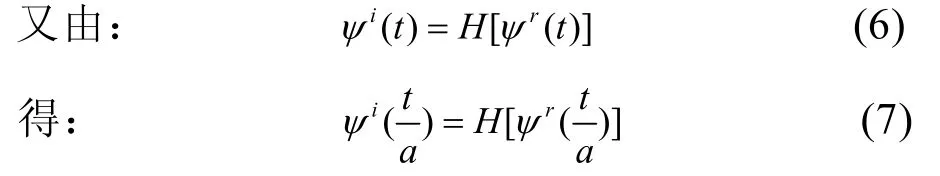
其中， H［·］表示Hilbert变换运算，因此有：

故信号x（ t）的Morlet小波变换系数的实虚部也是一对Hilbert变换，所以Morlet小波变换系数Wx（ a， b）的求模即可提取到Wxr（a， b）的包络，从而实现对信号的包络解调。

从以上分析可知，Morlet小波通过实虚部两次带通滤波构建了信号的解析信号，实现将带通滤波与包络解调两个过程合二为一。

2　基于Shannon小波熵自适应设计最优Morlet小波的方法

在突变信号的检测中，为了突出特征成分，可根据信号特征，自适应地选择最优带宽参数fb以使Morlet基小波与特征成分具有最大的相似性。Shannon小波熵［5，8］是一种评价相似的标准，其定义为：

Shannon小波熵值的大小反映了概率分布的均匀性，最不确定的概率分布（等概率分布）具有最大的熵值。当Shannon小波熵最小时，对应的Morlet基小波就是与特征成分最相似的小波。根据这一原理，可自适应设计出最优Morlet小波。

以仿真信号为例验证基于Shannon小波熵自适应设计最优Morlet小波有效性，设信号x（ t）为：

以1 Hz的频率对x（ t）采样1024点，其时域波形如图1所示。fb的取值范围为［1， 100］，步长为0.5，经计算可得到fb与Shannon小波熵之间的关系如图2所示。由图2知，fb=15时，具有最小的小波熵，对应的基小波就是与特征成分最匹配的Morlet小波，其小波变换时频图如图3（b）所示。作为对比，分别令fb取5和90，再作Morlet连续小波变换，时频图分别如图3（a）和3（c）所示。

图1　仿真信号时域波形

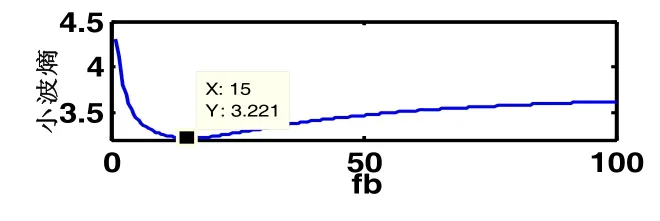
图2　fb与Shannon小波熵之间的关系曲线

图3　fb取不同值时的Morlet小波变换时频图

从图3可知，当fb取5时，信号的时间分辨率稍好于fb取15时的分辨率，但其频率分辨率比fb取15时的低，信号的高频分量与低频分量没有分开。当fb取95时，信号的频率分辨率稍好于fb取15时的分辨率，但其时间分辨率比fb取15时的低，以致信号的两个高频分量没有被分开。fb取15时，信号的时频聚集性最好，3个分量被清晰的区分开来。综合考虑时频分辨率，fb取15时为最优，因此，基于Shannon小波熵自适应设计最优Morlet小波的方法是有效的。

3　基于峭熵比的最佳尺度的求取方法

尺度为a的Morlet小波ψa（t）的中心频率为fc/a。在对信号作小波变换时，将各尺度的小波的中心频率fc/a预先归一化成一组固定值，信号的采样率与固定值的乘积即为相应尺度的小波系数的中心频率。故尺度a不仅控制滤波的频带范围，且滤波效果主要由带宽参数fb和尺度a决定。因此，设计出最优Morlet小波后，还须求取最佳尺度a，以将含有被调制信号信息最丰富的那个频段从强噪声背景信号中分离出来。

谱峭度（Spectral Kurtosis：SK）的本质为每根谱线处的峭度值，其计算公式为［9］：

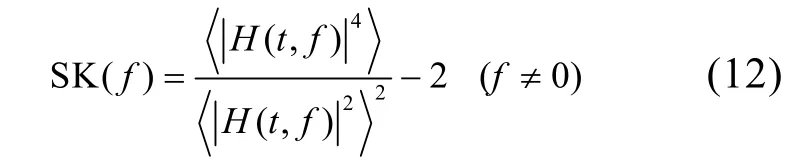
由前述，Shannon小波熵值的大小反映了小波系数分布的均匀性。故障冲击越强的频带，即是含有被调制信号的信息最丰富的频带，其信号幅值分布越不均匀，其谱峭度也越大，Shannon小波熵值越小，故Shannon小波熵值同谱峭度一样，也能反映信号中的冲击及其所在的频带。但实际信号分析表明，谱峭度的最大值与Shannon小波熵的最小值不一定在同一频带取到，也就是说基于谱峭度求取的最佳尺度与基于小波熵求取的最佳尺度不一定是同一尺度。鉴于此，综合考虑谱峭度与Shannon小波熵，本文提出一个新的冲击性评价指标——峭熵比，即谱峭度与Shannon小波熵的比值来衡量各个频带的冲击性。显然，冲击性越强的频带，其谱峭度越大，其Shannon小波熵值越小，因此其峭熵比也就越大。基于此，本文提出基于峭熵比的最佳尺度的求取方法，其基本步骤如下：1）先对信号进行最优Morlet小波变换；2）再用小波系数代替式（12）中的H（t， f ）计算各个尺度的谱峭度；3）再将各个尺度的小波系数的实部处理成一个概率分布序列并计算其Shannon小波熵，第j个尺度的Shannon小波熵计算公式为：

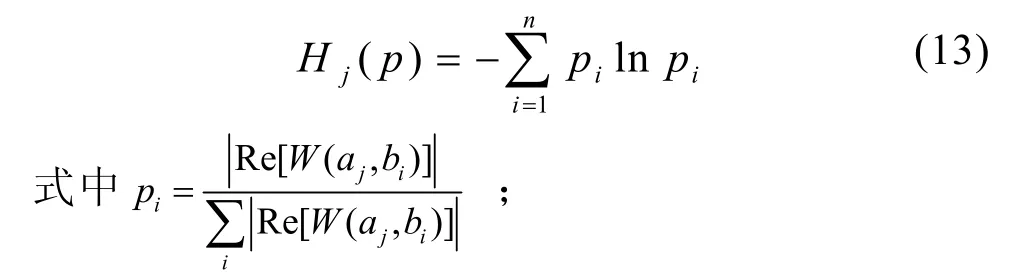
再依次计算各个尺度峭熵比，当峭熵比取得最大值时的尺度即为最佳尺度。

4　自适应Morlet小波包络解调的弱故障特征提取方法

为了有效地提取强噪声背景下的微弱故障特征和克服传统包络解调需要人为确定带通滤波器参数的不足，在前文研究基础上提出基于自适应Morlet小波包络解调的弱故障特征提取方法。该方法首先根据信号的特征成分采用Shannon小波熵方法优化带宽参数，自适应地设计出最优Morlet小波，并对信号进行最优Morlet连续小波变换，实现在全频带范围内对信号进行带通滤波。然后，依据峭熵比自适应地求取最佳尺度并提取最佳尺度的小波系数，从而实现对信号的最优带通滤波。最后，对最佳尺度的小波系数取模即可实现对最优频带的包络解调，提取到最优频带的包络，再对包络求频谱，即可得到包络谱，从而进一步提取到明显的微弱故障特征。

5　仿真实例

以仿真信号验证基于自适应Morlet小波包络解调的故障诊断方法的有效性。用类似于冲击信号的10个高斯原函数组成的信号叠加强噪声模拟实际故障振动信号（信噪比为-12.4dB），由下式给出：

式（14）中，ti=200， 400 …，2000，n（t）为强噪声。用fs=2048 Hz的采样率对x（t）进行采样，采样点数为2048点，采样信号及其频谱如图4所示。由图4时域图可知强背景噪声完全掩盖了冲击信号，因此对其故障冲击特征的提取是具有相当难度的。首先依据最小Shannon小波熵原理自适应设计最优Morlet小波。设母小波中心频率fc=0.5，各小波归一化的中心频率范围［0.005， 0.5］，步长为0.005，fb的范围［1， 100］，步长为0.5。依次计算各个fb对应的Shannon小波熵得到fb与Shannon小波熵之间的关系如图5所示。由图5可知，fb=17时，具有最小的小波熵，其对应的基小波就是与特征成分最匹配的最优Morlet小波。设计出了最优Morlet小波，然后基于峭熵比的方法求取最佳尺度。各尺度的峭熵比与尺度的关系如图6所示。由图6可知，峭熵比在中心频率为256 Hz的频带取得最大值，因此基于峭熵比求取方法求得的最优变换尺度为fs·fc/256=4。此尺度的中心频率即是各尺度的中心频率离振动固有频率250 Hz最近的频率，所以其中必然包含了最为丰富的故障冲击调制信息。

图4　含强噪声的模拟故障信号

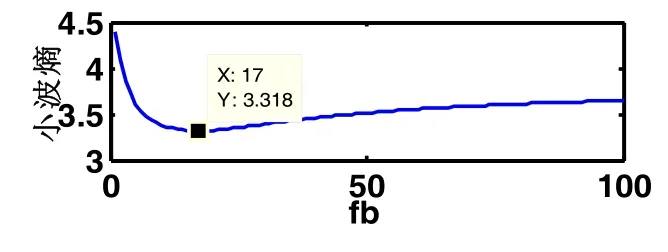
图5 fb与Shannon小波熵的关系

设计出最优Morlet小波和求取最优变换尺度后，下面对原始信号进行最优Morlet连续小波变换并提取最佳尺度的小波系数。尺度为4的小波系数的实部及其频谱如图7所示。从图7可以看出，最优Morlet小波有非常好的带通滤波性能，将包含故障调制信息最多的频带从包含强噪声的原始信号频谱中完美分离出来，充分的降低了最优频带中的噪声以致其小波系数中清晰地出现了间隔约为0.1s的冲击，这是非常有利于提取微弱故障特征的。对最佳尺度的小波系数取模即可得小波系数的包络，再对包络求傅里叶变换即可得相应的包络谱。尺度为4的小波系数包络和包络谱如图8所示。从图8中可知，尺度为4的小波系数的包络谱在故障冲击频率10 Hz及其倍频处出现很明显的谱线，这说明自适应Morlet小波包络解调已相当成功的提取到了隐藏在强噪声背景下的微弱故障冲击特征。

图6　各尺度的峭熵比与尺度的关系

图7　最佳尺度的小波实部系数及其频谱

图8　最佳尺度的小波系数实部包络及包络谱

从以上分析过程可知：1）最优Morlet小波有非常好的带通滤波性能和降噪能力，这非常有利于弱故障特征的提取；2）自适应Morlet小波包络解调能根据信号特点自适应设计最优Morlet小波并在全频带内自适应选择最优频带进行包络解调，无须人工设定滤波中心频率与带宽，便于用计算机进行故障自动识别。

以上仿真表明，自适应Morlet小波包络解调的弱故障提取方法能有效的隐藏在强噪声背景下的微弱故障特征。

6　结论

综合本文可得如下结论：

1）根据信号自身的冲击特征，采用基于Shannon小波熵的方法优化了带宽参数设计了最优Morlet小波，自适应地实现其与冲击特征成分的最优匹配。

2）利用谱峭度与小波熵均能敏感反映冲击性的特性，提出基于峭熵比的新方法来求取最优变换尺度。该方法综合考虑了谱峭度与小波熵两种指标，能方便有效的求出最优变换尺度，具有一定的工程应用价值。

3）提出基于自适应Morlet小波包络解调的弱故障特征提取方法。仿真实验分析表明：该方法无须人工设定滤波中心频率与带宽，能自动有效地从强噪背景中提取微弱故障特征，具有一定的工程应用价值。

［1］ Y Yang， D J Yu， Js Cheng. A fault diagnosis approach for roller bearing based on IMF envelopespectrum andsVM［J］. Measurement， 2007， 40（9）： 943-950.

［2］ 苏文胜， 王奉涛， 张志新， 等. EMD降噪和谱峭度法在滚动轴承早期故障诊断中的应用［J］. 振动与冲击， 2010， 3（29）： 18-21.

［3］ Yuh-Taysheen. On thestudy of applying Morlet wavelet to the Hilbert transform for the envelope detection of bearingVibrations［J］. Mechanicalsystems andsignal Processing， 2009， 23（5）： 1518- 1527.

［4］ 程发斌， 汤宝平， 钟佑明. 基于最优Morlet小波和SVD的滤波消噪方法及故障诊断的应用［J］. 振动与冲击， 2008， 27（2） ： 91-94.

［5］ JIN L，LIANGSHENG Q U.Feature extraction based on morlet wavelet and its application for mechanical fault diagnosis［J］.sound andVibration， 2000， 234（1）： 135-148.

［6］ 何岭松， 李巍华， 用Morlet小波进行包络检波分析［J］，振动工程学报，2002，15（1）： 119-122.

［7］ 蒋永华， 汤宝平， 董绍江. 自适应Morlet小波降噪方法及在轴承故障特征提取中的应用［J］. 仪器仪表学报， 2010， 31（12） ： 2712-2717.

［8］ NIKOLAOU N G，ATONIADIS I A.Demodulation ofVibrationsignals generated by defects in rolling element bearings using complexshifted morlet wavelets［J］. Mechanicalsystems andsignal Processing， 2002，16（4）： 677- 694.

［9］sawalhi N， Randall R B， Endo H. The enhancement of fault detection and diagnosis in rolling element bearings using minimum entropy deconvolution combined withspectral kurtosis ［ J］. Mechanicalsystems andsignal Processing， 2007， 21（6）： 2616- 2633.

The Method to Extract Weak Fault Feature Based on Adaptive Morlet Wavelet Envelope Demodulation

Niu Chao， Hou Xinguo， Yang Zhonglin
（College of Electrical Engineering， Naval University of Engineering， Wuhan 430033， China）

In order to achieve adaptive optimal match with the impact component，shannon wavelet entropy is used to optimize bandwidth parameter of the Morlet wavelet to design the optimal Morlet wavelet. Aimed at the problem of obtaining the optimalscale， the new approach which is based on kurtosis entropy ratio to acquire the optimalscale is presented. In addition， the new method to extract weak fault feature based on adaptive morlet wavelet envelope demodulation is proposed in the paper. Thesimulation results and analysis on the incipient fault data of ball bearingshow that the method overcomes the defect that the parameters of band-pass filter areselected by experience of the user in conventional envelope demodulation， decreases the dependence on user， and can automatic and effectively extract the weak fault feature.so， the method hassome applicationValue.

Morlet wavelet； adaptive envelope demodulation；shannon wavelet entropy； kurtosis entropy ratio；spectral kurtosis

TM712

A

1003-4862（2015）10-0026-05

2015-03-14

牛超（1982-），硕士研究生。研究方向：信号检测与处理，设备的故障诊断等。