一种简易核磁共振实验教学仪器

殷正保，王连水，王　俊

（1.中国船舶重工集团公司第七一〇研究所，湖北宜昌 443003；2.华中科技大学，武汉 430081）

一种简易核磁共振实验教学仪器

殷正保1，王连水2，王俊1

（1.中国船舶重工集团公司第七一〇研究所，湖北宜昌 443003；2.华中科技大学，武汉 430081）

自制了一种连续波核磁共振教学实验仪器，包括设计了简单的背景磁场，以及自制实验仪器探头。

核磁共振永久磁铁均匀磁场边限振荡器

0　引言

随着核磁共振方法在各个领域的广泛应用，核磁共振实验已经成为很多学校工科学生必做的实验。然而，截止到现在，核磁共振设备还是有很高的行业门槛和技术壁垒，所以仪器依然很昂贵。其中包括很高的磁场均匀度、高输入信噪比的探头以及足够频率稳定度的射频等。很多人认为，核磁共振的主要成本集中在磁体上，所以必须把主要精力花在磁场上，才能降低仪器成本。但是仪器其它部分的重要性也不容忽视，比如探头。探头是检测部分的最前端，其性能的好坏关系到能否得到高质量的信号。如果探头做的不好，磁场均匀度再高，信号质量也将会大打折扣。本文设计了一种小型的连续波核磁共振实验仪器，主要包括磁场与探头的设计。其中，对传统的仪器作了一些改进，主要是对仪器探头的改进，从而降低对背景磁场强度和均匀度的要求。经过简单的水样品实验，得到了较高信噪比的信号，证明了设计的可行性。

1　检测原理与装置

核磁共振现象是静磁场下原子核吸收特定频率电磁波产生能级跃迁引起的。吸收的射频频率必须等于共振频率，才能产生共振现象。共振频率与静磁场满足拉莫尔方程：

为了满足这个条件。目前，连续波核磁共振实验仪器一般采用调场法[1]观察信号。具体方法是在静磁场 B0上叠加一个低频调制磁场Bmsinω’t。叠加后样品所在区域的实际磁场为即：

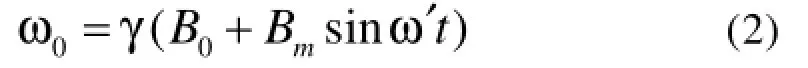
从(2)中看出，共振频率 ω0的变化范围为[γ(B0- Bm)，γ(B0+ Bm)]。在示波器上采集到的共振吸收信号如图1中（b）所示。此时，若调节射频场的频率，示波器采集到的吸收峰间距相等时信号特征如图1（a）所示，则说明在这个频率下的共振磁场为B0。

图1　调场法原理

整个实验装置由磁体部分和探头部分组成，如图2所示：

图2　实验装置框架示意图

其中，虚线框中展示的为磁体部分，由调场线圈，匀场装置、主磁体等组成。主磁场B0由主磁体产生。匀场装置负责辅助主磁体使磁场调制的更加均匀。调场线圈是负责施加低频调制磁场，使共振频率与射频频率同步。

探头部分是虚线框外部分（显示部分除外），包括样品部分和电路部分组成。样品放置于试管中，试管外绕制调场线圈用于产生和接收核磁共振信号；电路部分主要用于产生振荡信号并检测核磁共振信号，本实验采用单线圈探头，电路部分采用边限振荡器方法实现。

2　磁体设计

主磁体选用永磁体，永磁体具有造价低，结构简单，维护成本低廉等优点。为了使装置尽量小型化，以及使成本尽量低，选用强磁材料钕铁硼作磁体。主磁体的设计主要是根据磁路基尔霍夫定律设计磁路尺寸。

首先，必须确定磁场指标。为了使仪器小型便携，对磁体部分以及工作气隙提出以下要求：

背景（气隙）场强Bg：0.6-0.7 T；

在10 mm×10 mm×10 mm的体积内磁场均匀度：约为10-3；

磁体重量：≤20 kg；

整体体积：≤300×3000×300 mm3；

气隙大小为：75 mm×75 mm×30 mm （方形磁体）。

设计过程如下：

其中，σ为漏磁系数，f 为磁阻系数，根据经验获得，这里取 σ=1.4，f=1.2。Sg为气隙截面积。Bm，Hm分别为磁体内部磁感应强度与磁场强度。Lm磁极的长度。Se为磁路轭铁厚度。

考虑漏磁后磁路的基尔霍夫定律为：

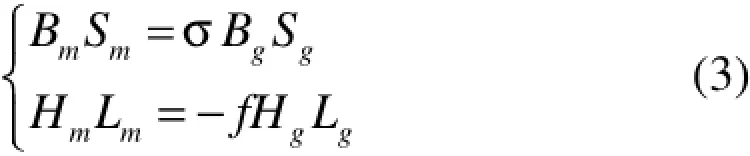
根据设计指标要求，已知条件有：

其中，Lg为气隙长度；am为磁极边长；Sm为磁体截面积。

考虑到漏磁，气隙截面的有效面积应该比磁体的截面大：

其中，K为调节系数，取0.2。根据磁路基尔霍夫定律可以得出磁极的磁感应强度：

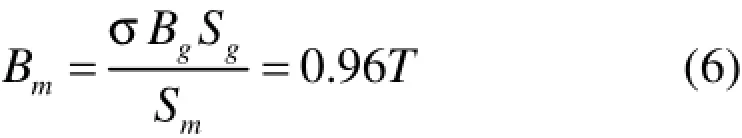
磁极长度的计算可根据磁路基尔霍夫，其中Bm为0.96T时的磁场强度可以据（图3）钕铁硼材料的退磁曲线查询可得，约为239 kA/m。

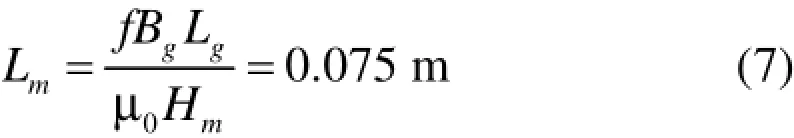
根据上述计算结果，单块磁极大小确定为37.5 mm。

图3　钕铁硼材料退磁曲线

接下来进行铁轭结构设计。

铁轭的作用是构成磁体结构框架并构成导磁回路，材料选用普通碳素钢Q235。铁轭设计必须考虑强度和材料磁饱和两个方面的问题，一般情况下只需要考虑磁饱和问题。

铁轭需要有足够的横截面积才能避免由于磁饱和而引起磁导率下降进而造成磁路磁阻增加的现象。

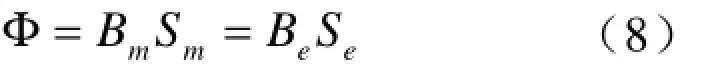
可以计算出铁轭厚度为12.5 mm。

以上设计的结构必然会产生漏磁，所以必须对磁场均匀度进行补偿，才能达到核磁共振要求的均匀度。本设计采用无源补偿，采用 Maxwell 2D仿真软件，对磁场进行仿真，使补偿尽量优化。无源补偿的极靴形状如图 4。补偿之前与补偿后仿真结构如图 5，图 6。可以看出均匀度从约为2%提高到0.1%。

图4　极靴形状

调制的磁场精确度要求并不是很高。我们只需要事先确定线圈的型号及匝数，再通过理论计算校核磁场是否满足试验要求。实际操作中，我们选用线径0.8 mm，电流密度为2.5 A/mm2的21号线圈，查表可得线圈直流阻抗 0.043 Ω/m，允许最大电流1.26 A，这里附加可调电阻调节电流。两边各绕制270匝套磁极外部。

3　探头设计

根据核磁共振原理，核磁共振吸收信号的大小可用吸收磁化率共振χ”来表征。共振吸收会引起阻抗Z、Q值、谐振频率等谐振回路的相关参数改变。其中Q值变化用δ (1/Q)表示，其大小与吸收磁化率χ”呈正比[2]：

其中，η为样品填充因子。谐振槽路阻抗的变化与Q的变化相关，其关系为Qδ (1/Q)。当发生核磁共振吸收时，谐振槽路两端的电压变化与阻抗变化相等，两者存在以下关系：

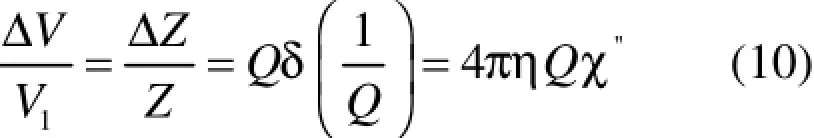
因此，可以得出核磁共振吸收信号的大小（均方根）：

而探头均方根噪声可以用如下公式来描述：

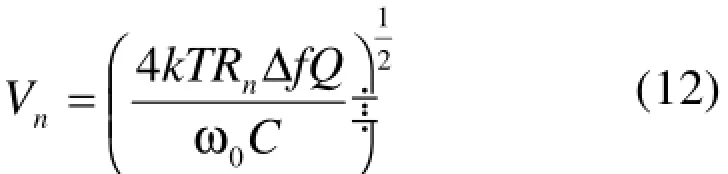
其中，T为探头的开尔文温度；C为调谐电容；Rn为等效损耗电阻；ω0为共振频率。

图5　未补偿时的样品区的磁场强度

图6　补偿调整后样品区的磁场均匀度

因此，探头的输入信噪比可以用以下公式来表述：

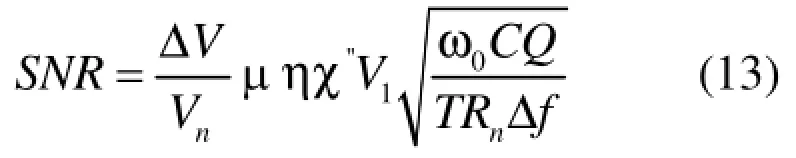
其中，多数因素比较难确定。比如，T小了，信噪比提高了，但是成本提高了；V1大了，信噪比也提高了，但是太大了又产生有饱和问题。只有参数等效损耗电阻Rn比较明确：应该尽量小。而且Rn对信噪比的影响也是显著的。

谐振槽路等效损耗电阻[3]（如图 7）主要由样品损耗 Rsample，线圈电阻 Rcoil，调谐电容的高频损耗Rcap以及线圈的引线电阻Rlead共同组成。以下是谐振槽路的等效噪声模型（在电容Q值远大于1的条件下，串联谐振与并联谐振都适用）。

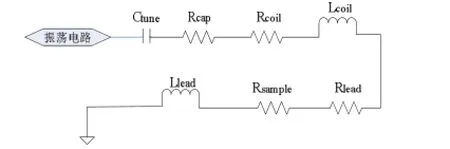
图7　噪声计算等效模型

其中，电容损耗主要由电容介质消耗电场能量引起的，样品损耗是电磁场在传输过程中消耗能量引起的。两者在总体损耗中所占的比例很小，一般可以不予考虑。因此，实际情况下线圈总损耗大致与探头的等效损耗电阻相等，即线圈电阻与引线电阻之和。其中，引线电阻与引线长度成正比。所以，必须尽量缩短引线长度。

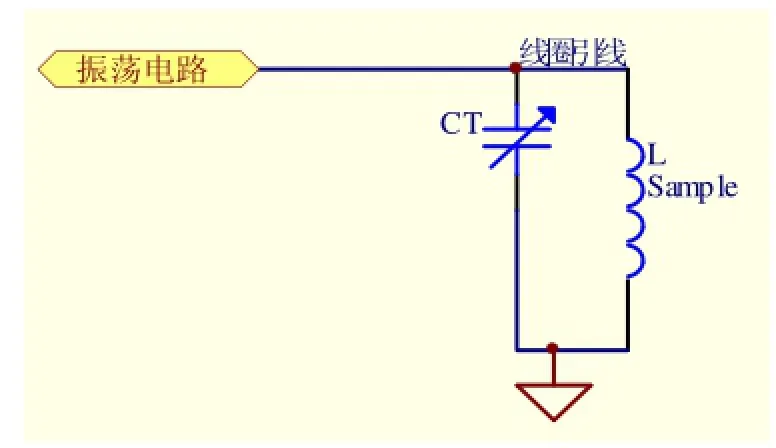
图8　传统探头结构

传统的连续波实验仪器探头设计（如图8所示）基本上都是线圈引线直接接振荡电路，这样就会导致引线长度很长。而长的引线使探头的输入信噪比变差，而且导致射频频率很不稳定。而本文采用的设计是用屏蔽线来代替线圈引线（如图9所示），有效的缩短了引线长度，而且起到屏蔽干扰的作用，解决了传统仪器探头的不足。此外，调谐操作变得容易，可以采用高Q值的可变电容代替低Q值的变容二极管调谐。

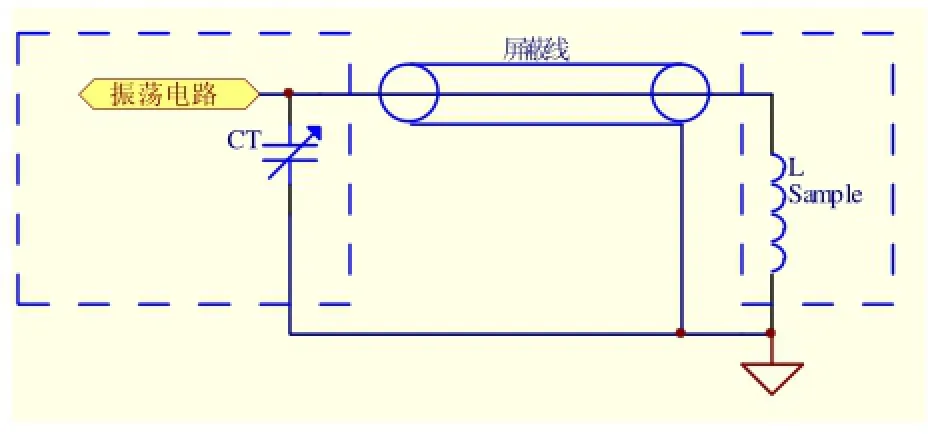
图9　改进探头结构

接下来是电路部分的设计。电路部分主要以边限振荡器为中心，这里只介绍边限振荡器的设计，检波电路与放大电路都采用常用电路。传统边限振荡电路采用如图10所示的形式，这种电路有两个缺点：

图10　改进前的边限振荡器电路

1）探头的震动已经低频调制场场会给电路带来很大的干扰。

2）通过调节源级电阻 R3（即调节静态工作点）来达到边限振荡状态，会引起波形失真，造成频率不稳定。

针对以上两个缺点，本设计对边限振荡器作了以下方面改进：

1） 在调谐回路与振荡电路之间加了一级低频滤波电路，这样可以有效滤除低频调制场干扰和颤噪干扰。

2） 在反馈回路加了电阻反馈，通过调节反馈电阻使电路达到边限振荡状态，可以显著改善射频的稳定性。

改进后的振荡器如图11所示。

4　性能测试

自制的核磁共振磁体如图 12所示。采用高斯计测量，磁场大小为0.68 T（对于质子，共振频率为28.95 MHz），磁场均匀度约为0.1%，达到我们的设计要求。

图11　改进后的边限振荡器电路

图12　仪器磁体装置

图13　仪器探头

采用改进的实验探头与振荡器电路，调节后能得到如图14所示的信号。从图中，可以看实验得到的信号具有比较高的信噪比。

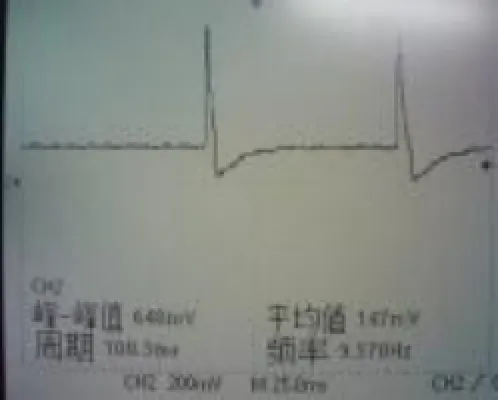
图14　实验结果

5　结论

通过简单的样品进行实验，证实小型的核磁共振装置能够达到较高信噪比信号。由于探头具有较高输入信噪比，实验仪器对其它部分（如磁体）的要求可以适当降低，从而使仪器的成本得到降低，使实验仪器能够得到更大范围的推广。

[1] 吕斯骅，段家忯. 新编基础物理实验. 北京: 高等教育出版社，2006.

[2] F. N. H. Robinson. Nuclear resonance absorption circuit.Rev. Sci. Instrum，1959，36: 481-487.

[3] Yu Li. Design and optimization of high-sensitivity probes for improved limits of detection in protein nuclear magnetic resonance spectroscopy. 2000.

[4] 王乐，宋枭禹，朱海涛等. 用永磁材料改善永磁MRI的主磁体极面[J]. 中国医学影像技术，2006，22 （7）: 151-153.

[5] 王蔷，李国定，龚克. 电磁场理论基础[M]. 北京:清华大学出版社，2000.

[6] 毛希安. 现代核磁共振实用技术及应用[M]. 北京:科学技术文献出版社，2000.

[7] F.N.H. Robinson. Nuclear resonance absorption circuit[J]. Rev. Sci. Instr-um，1959，36: 481-487.

A Portable Nuclear Magnetic Resonance Spectroscopy for Teaching

Yin Zhengbao1，Wang Lianshui2，Wang Jun1
（1. No. 710 R&D Institute，CSIC，Yichang443003，Hubei，China; 2. Huazhong University of Science and Technology,Wuhan 430074，China）

In this paper，a low-cost and miniature NMR(Nuclear Magnetic Resonance) spectroscopy for teaching is designed. The probe and circuit part are designed，and the magnetic field is built. The permanent magnet is chosen to construct the magnetic field in magnetic part. According to the water sample detection and the display of oscillograph signal，the high-quality continuous wave NMR signal may be gained.

NMR (Nuclear Magnetic Resonance)，permanent magnet，uniform magnetic field，marginal oscillator

TP307

A

1003-4862（2015）12-0044-05

2015-03-14

殷正保（1984-），男，工程师。研究方向：无源电子对抗行业。

用示波器观测信号，经过简单的水样品的实验，结果证明，仪器能够得到高质量的连续波核磁共振信号。