半挂汽车列车牵引车后轮转角最优控制设计

刘春辉，关志伟，杜峰

（天津职业技术师范大学汽车与交通学院，天津300222）

半挂汽车列车牵引车后轮转角最优控制设计

刘春辉，关志伟，杜峰

（天津职业技术师范大学汽车与交通学院，天津300222）

选取牵引车质心侧偏角、横摆角速度、半挂车横摆角速度及牵引车与半挂车的中心线夹角为状态变量，利用线性二次型最优控制理论求解牵引车后轮转角，实现半挂汽车列车四轮转向的最优控制。在Matlab/Simulink仿真软件中对四轮转向半挂汽车列车改善侧向稳定性的有效性进行验证。仿真结果表明：基于状态反馈的四轮转向半挂汽车列车在高速大转角的极端情况下能保证转向行驶的稳定性。

四轮转向；状态反馈；最优控制；仿真

半挂汽车列车由于其结构特点，相比传统的2轴乘用车，其动力学特性更为复杂，失稳形式更为多样，失稳后引发的交通事故危害更大。随着半挂汽车列车行驶速度的不断提高，由其造成的交通事故越来越多。目前，半挂汽车列车的安全问题引起了人们的广泛关注，针对半挂汽车列车的主动安全问题也已经提出了多种控制策略［1-6］，四轮转向技术是其中一种比较有效的控制策略。四轮转向半挂汽车列车是将牵引车前、后轮同时作为转向轮，从而有效改善其高速行驶时的侧向稳定性。本文基于线性二次型最优控制理论求解半挂汽车列车牵引车的后轮转角以追踪理想模型，利用Matlab/Simulink数值仿真平台，对牵引车后轮转角实施主动控制的半挂汽车列车进行时域仿真，对四轮转向改善半挂汽车列车高速大转向行驶时侧向稳定性的效果进行分析。

1　牵引车后轮转角的最优控制算法

牵引车前、后轮同时作为转向轮的四轮转向半挂汽车列车非线性动力学模型见文献［7］，该模型包括牵引车和半挂车的侧向运动和横摆运动，具有4个自由度。考虑轮胎的侧向力与轮胎侧偏角和轮胎侧偏刚度成正比（线性轮胎模型），可将四轮转向半挂汽车列车非线性动力学模型转化为四轮转向半挂汽车列车线性模型，状态变量选为牵引车质心侧偏角β1、牵引车横摆角速度r1、半挂车横摆角速度r2及牵引车与半挂车的中心线夹角θ，通过推导可得出其状态空间表达式（半挂汽车列车线性模型）见文献［6］。

本文利用线性二次型最优控制理论在半挂汽车列车线性模型基础上求取最优后轮转角δbw1以追踪参考模型，从而改善半挂汽车列车的侧向稳定性。

若参考响应以下标d表示，参考模型可在半挂汽车列车线性模型的基础上简单表示为［8］：

式中：Xd=［β1dr1dr2dθd］T；Ad=Aac；Bd=Bac；Cd=Cac1。

以Δ表示各变量的差值，令X=［Δβ Δr1Δr2Δθ］T= Xac－Xd，则有：

二次型性能泛函的表达式J为：

式中：Q为半正定常数矩阵；R为正定常数矩阵。

最优控制存在且唯一，反馈输入δbw1可写为如下形式：

式中：P为正定常数矩阵，满足黎卡提矩阵代数方程：

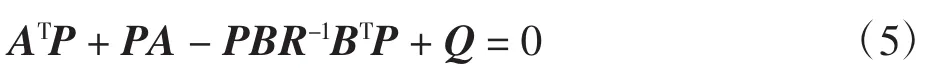
2　仿真分析

仿真过程采用如下车辆参数：牵引车质量m1= 6 870 kg、半挂车质量m2=6 181 kg；牵引车绕质心转动惯量IZ1=20 441 kg·m2、半挂车绕质心转动惯量IZ2= 81 912 kg·m2；牵引车质心到前轴的距离a1=1.96 m、牵引车质心到后轴的距离b1=2.35 m、半挂车质心到半挂车车轴的距离b2=3.30 m、牵引车质心到铰接点的距离c1=2.05 m、半挂车质心到铰接点的距离c2= 5.23 m；牵引车后轮侧偏刚度Cr1=143.33 kN/rad、半挂车车轮侧偏刚度Cr2=80.312 kN/rad、牵引车前轮侧偏刚度Cf1=143.33 kN/rad。

仿真过程以单周期正弦信号作为前轮转角的输入，最大幅值为0.135 rad；取半挂汽车列车行驶速率为30 m/s，仿真时间为10 s。牵引车质心侧偏角、横摆角速度、半挂车横摆角速度及牵引车与半挂车中心线夹角的仿真结果对比如图1至图4所示。

从图1至图4可以看出，在给定的条件下，传统前轮转向（FWS）半挂汽车列车的牵引车质心侧偏角于2.5 s左右急剧变化，随后横摆角速度、半挂车横摆角速度及牵引车与半挂车中心线夹角也在4 s左右急剧变化，表明此时半挂汽车列车很快失去稳定性；而基于最优控制的四轮转向半挂汽车列车的牵引车质心侧偏角、横摆角速度，半挂车横摆角速度及牵引车与半挂车的中心线夹角均能紧紧跟随参考值的变化，约在5 s左右，所有状态变量均稳定下来，实现了半挂汽车列车高速大转角极限工况行驶的稳定性。

图1　牵引车质心侧偏角响应比较

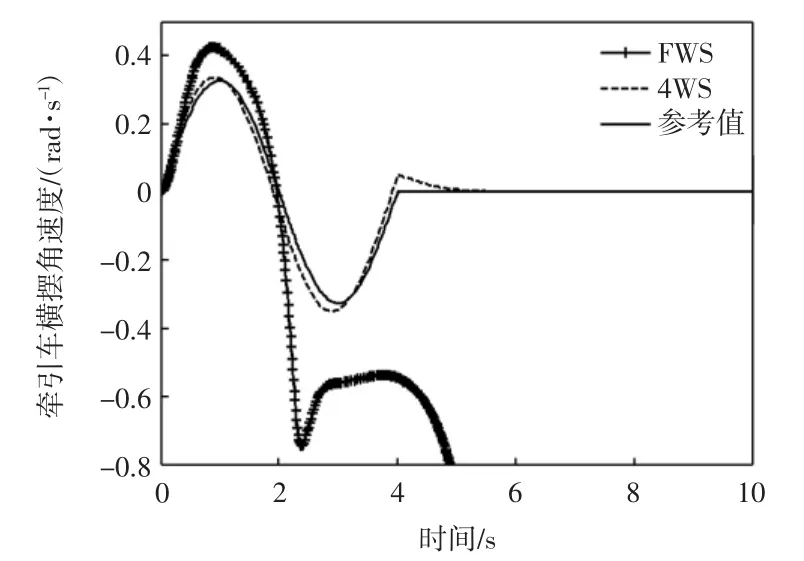
图2　牵引车横摆角速度响应比较

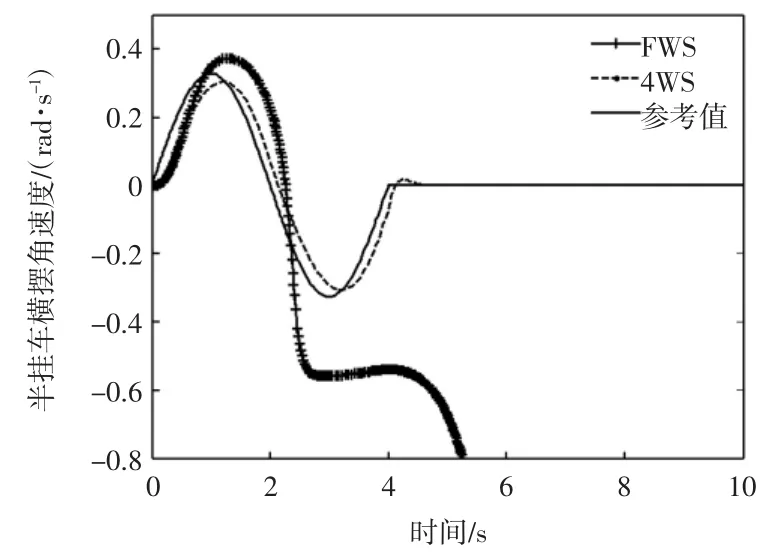
图3　半挂车横摆角速度响应比较

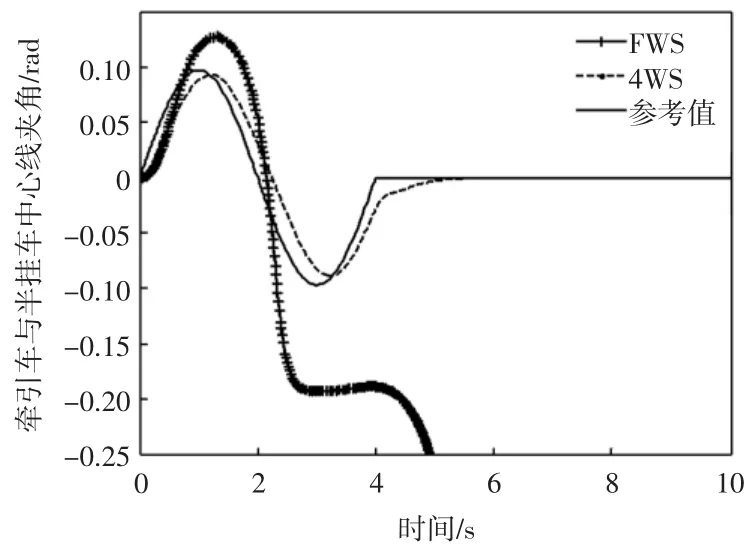
图4　牵引车与半挂车中心线夹角响应比较

基于状态反馈的牵引车后轮转角的变化值如图5所示。从图5可以看出，随着半挂汽车列车各状态变量的变化，牵引车后轮转角也随之发生相应变化，该变化在5 s左右稳定下来，此时半挂汽车列车稳定行驶。

图5　牵引车后轮转角

3　结束语

本文基于线性二次型最优控制理论求取了半挂汽车列车牵引车的最优后轮转角，在Matlab/Simulink中对四轮转向半挂汽车列车在高速大转向条件的极限工况下改善侧向稳定性进行了仿真验证。仿真结果表明实施牵引车后轮转角主动控制的四轮转向半挂汽车列车能有效提高极限工况下的侧向稳定性，为行车安全提供了保障。

［1］ELHEMLYMAE，FAYEDMAG.Simulationoftractor semitrailer manoeuvre at high speed using Matlab/Simulink［J］. International Journal of Heavy Vehicle Systems，2011，18（40）：341-358.

［2］NAGAI M，HIRANO M，YAMANAKA S.Integrated control ofactiverearwheelsteeringanddirectyaw moment control［J］. Vehicle System Dynamics，1997，27（5/6）：357-370.

［3］NAGAI M.The perspectives of research for enhancing active safety based on advanced control technology［J］.Vehicle System Dynamics，2007，45（5）：413-431.

［4］ESMAILZADEH E，GOODARZI A，VOSSOUGHI G R.Optimal yaw moment control law for improved vehicle handling［J］. Mechatronics，2003，13（7）：659-675.

［5］杨秀建，杨春曦，张弦，等．基于主动制动的半挂汽车列车横摆稳定性控制［J］．汽车工程，2011，33（6）：486-492．

［6］刘春辉，关志伟，杜峰，等.半挂汽车列车横向稳定性的最优控制［J］.机械科学与技术，2012，31（10）：1694-1697.

［7］刘春辉，关志伟，杜峰，等.四轮转向半挂汽车列车横向稳定性仿真分析［J］.系统仿真学报，2013，25（5）：1127-1129.

［8］杨秀建，王增才，路玉峰，等．极限工况下汽车稳定性的最优保性能控制［J］．农业机械学报，2008，39（6）：38-41.

Optimal control of rear steering angle of the tractor of tractor-semitrailer

LIU Chun-hui，GUAN Zhi-wei，DU Feng
（School of Automobile and Transportation，Tianjin University of Technology and Education，Tianjin 300222，China）

Choosing slip angle of tractor，yaw velocity of tractor and semitrailer，and using angle of tractor and semitrailer as control variables，the optimal control scheme is proposed to realize the rear steering angle of the tractor.Based on the established nonlinear dynamic model，simulation of the four-wheel steering tractor-semitrailer in matlab/simulink software environment is described.The simulation consults show that for the four-wheel steering tractor-semitrailer，the handling and stability performance on big slip angle is improved.

four-wheel steering；state feedback；optimal control；simulation

U463.4

A

2095－0926（2015）04－0043－03

2015-09-18

天津职业技术师范大学科研发展基金项目（RC14-13）.

刘春辉（1983—），男，讲师，研究方向为汽车系统动力学仿真与控制.