一种加入局部搜索的双子代差异演化算法

武志峰，刘烁，李耀辉

（天津职业技术师范大学信息技术工程学院，天津300222）

一种加入局部搜索的双子代差异演化算法

武志峰，刘烁，李耀辉

（天津职业技术师范大学信息技术工程学院，天津300222）

针对差异演化算法存在收敛速度慢的问题，提出一种加入局部搜索算子的双子代竞争差异演化算法。为了增加群体多样性，对初始种群采用等间隔均匀分布。算法对每一代演化种群中的最优个体以一定概率加入局部随机扰动，在其附近搜索更优秀的新个体，以加快发现最优解的速度。在7个常用测试函数上的实验结果表明：无论是在最优解质量、收敛速度，还是在平均评价次数等方面，本文算法都优于文献［5］的算法。

差异演化；局部搜索；全局优化

1995年，Storn和Price［1］提出了一种新型的演化算法—差异演化（differential evolution，DE）算法。该算法的基本思想是利用种群中个体的差异进行演化。与遗传算法类似，该算法也是通过对种群的交叉、变异、选择等操作生成下一代种群。与遗传算法不同的是，差异演化算法的变异操作是基于群体差异性来修正各个体的值，即利用群体中个体的“差异”作为向最优解搜索的主要动力源。对群体中的每个个体算法随机选择几个不同的个体，并由它们的“差异”生成试验向量，然后再以一定的交叉概率与该个体离散交叉生成新个体，最后通过“贪婪式”的选择方法，保留原个体和新生成个体中的优秀者。在首届IEEE演化计算大赛中，差异演化算法是所有参赛算法中进化速度最快的不确定搜索方法，表现出卓越的性能，随后在各领域得到广泛的应用［2］。

虽然差异演化算法对于非凸、多峰等非线性的函数优化问题具有不错的性能，但基本差异演化算法对一些复杂的大规模优化问题，其前期收敛速度较慢，后期由于种群趋于同化，算法易陷入局部最优解，使算法的稳定性、求解精度等不尽人意。目前，学界已提出许多方法来改进差异演化算法的性能。文献［3］利用个体向量的邻域概念把变异算子分为邻域内的局部变异和群体内的全局变异，以改进算法的性能。文献［4］提出一种双种群差分进化规划算法。该算法将种群划分为2个子群独立进化，分别采用DE/rand/1/bin和DE/best/2/bin版本生成变异个体。之后将2个子群合并为一个种群，再应用混沌重组算子将之重新划分，以实现子群间的信息交流。同时用非均匀变异算子对其最优个体执行进化规划操作，使算法具有较快的收敛速度和较强的全局寻优能力。文献［5］提出一种带惯性变异与正交设计的差分进化改进算法。该算法利用正交设计方法在群体中最优个体的局部邻域内进行搜索，以提高最优解的搜索速度。文献［6］提出一种基于分工的差分进化算法。在进化过程中对个体进行分工，优秀个体选择best/1策略承担开发任务，一般或较差个体选择rand/1变异策略承担探索任务，通过个体分工负责提高算法性能。文献［7］提出一种基于Boltzmann机制的双子代竞争差异演化算法。与以往算法不同，该算法的交叉操作可以生成2个新个体，然后2个个体与父代个体一起竞争形成子代个体。同时引入Boltzmann机制，使算法可以跳出局部最优解，从而找到全局最优。文献［8］提出了一种基于动态局部搜索的差分进化算法，增加种群的多样性，平衡算法的开发能力和探索能力。文献［9］提出一种随机变异差异演化算法，改进了差异演化算法的变异操作。

本文在文献［7］的基础上，采用rand/1变异策略，在交叉生成双子代竞争个体的同时，对每一代中的最优个体加入局部搜索方法，承担开发任务，加快最优解搜索。同时，为保证种群的多样性，在种群初始化时实行均匀分布，即在自变量的可行域内按照种群规模均匀设置每个个体。在7个常用基准测试函数上的实验结果表明，该算法在最优解质量和收敛速度上都具有很好的效果。

1　差异演化算法

差异演化算法是一种类似遗传算法的以实数编码的演化算法。与遗传算法的主要区别是其变异操作基于个体的差异向量进行。差异演化算法实质上是一种自适应的迭代寻优随机搜索算法。其基本思想是从初始种群开始，把任意2个个体的向量差加权后与第3个个体求和形成变异个体，再将变异个体与当前种群中的某一指定个体进行交叉操作生成试验个体，然后在指定个体和试验个体之间选择适应值较优的个体作为新一代的个体。通过不断地迭代，算法使种群中优良个体得以保留，劣质个体逐渐淘汰，从而引导搜索过程向最优解逼近。

令xi（t）是第t代的第i个染色体，则xi（t）=（xi1（t），xi2（t），…，xin（t））（i=1，2，…，M；t=1，2，…，tmax）。其中：n为染色体的长度，即变量的个数；M为种群规模；tmax为最大的进化代数。

基本差异演化算法框架描述如下：

步骤1设置算法相关参数。参数包括种群规模M，缩放因子F和交叉因子CR等。

步骤2生成初始种群。随机生成满足约束条件的M个个体构成初始种群。

步骤3变异操作。从种群中随机选择3个个体xp1、xp2、xp3且i≠p1≠p2≠p3，则

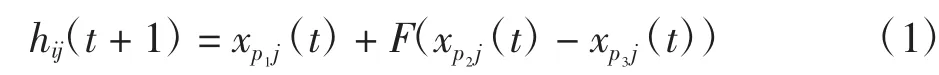
步骤4交叉操作。把变异操作生成的个体与指定目标个体做如下交叉操作：

式中：rand1ij为随机数，rand1ij∈［0，1］；CR为交叉概率，CR∈［0，1］；rand（i）为在［1，n］之间的随机整数。这种交叉策略可确保vi（t+1）中至少有一个分量由hi（t）的相应分量贡献。

步骤5选择操作。对新个体vi（t+1）和目标个体xi（t）进行评价，择优生成下一代个体：

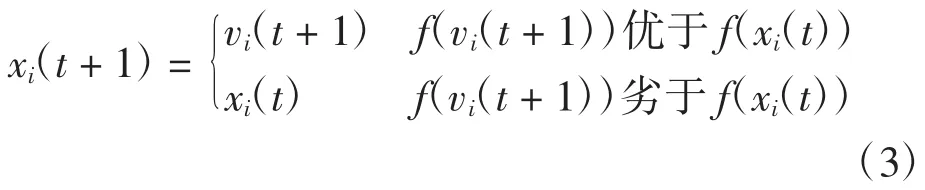
步骤6反复执行步骤3至步骤5操作，直至达到最大进化代数。

2　加入局部搜索的双子代差异演化算法

2.1算法基本思想

由式（1）可知，在rand/1变异策略中，新的变异个体由3个完全不同的随机个体组成，因而有利于保持种群的多样性。这使算法的全局搜索能力较强，但同时也会导致算法收敛速度慢、精度低、搜索效率低下。此外，传统的差异演化算法在生成初始种群时多使用随机初始化的方法，从而导致初始种群在问题的解空间中不能均匀分布，进而影响到种群对问题解空间的全面搜索。文献［7］通过改进交叉和选择操作，提出一种基于Boltzmann生存机制的双子代竞争差异演化算法，增加了群体的多样性，从而使算法性能得到提高。但这种算法忽略了对种群中每个个体局部邻域的搜索，同样存在算法的收敛速度慢等问题，特别是在当前最好解非常接近最优解的时候，可能需要多次操作才能找到真正的最优解。而局部搜索算法是一种简单有效的寻找最优解的方法，可以在当前解的周围快速找到更好的解。本文提出一种加入局部搜索策略的改进算法，首先对种群在解空间内进行均匀初始化，保证种群在解空间中均匀分布；然后利用双子代策略生成新一代种群，并对其中的最优个体加入一定的局部搜索策略，在其周围进行局部开发，以期搜索到更好的解，从而使算法尽快收敛；同时为避免陷入局部极小值，算法并不是对每一代种群中的最优个体都进行局部搜索，而是以一定的概率，对其执行局部搜索算子，且随着演化代数的增加，其执行局部搜索算子的概率也不断加强。

2.2均匀初始化种群

为保证初始种群在问题解空间的均匀分布，算法没有采用随机生成初始种群的方法，而是根据种群规模把自变量的取值范围均匀分为若干段，然后在每一段区间上随机生成一个个体，从而保证了初始种群中每个个体在求解空间上分布的均匀性。例如，自变量X的取值范围为［a，b］，算法种群规模为popsize，则均匀初始化种群可描述如下：

输入：种群规模popsize，自变量下界a，自变量上界b；

输出：均匀初始化的种群population；

Function initPop（popsize，a，b）

｛

interval=（b-a）/popsize；

for（i=0；i＜popsize；i++）

｛

ai=a+i×interval；

bi=ai+interval；

for（j=0；j＜col；j++）|

population［i］［j］=random（）×（bi-ai）+ai；

｝

｝

2.3局部搜索算子

在经典的差异演化算法中，rand/1的变异策略使差异演化算法具有较强的全局搜索能力，但同时也会导致算法收敛速度变慢。特别是当问题的全局最优解就在当前最优解附近时，算法却可能还需要搜索多次才能得到全局最优解。为加快算法的收敛速度，本文算法对每一代种群中的最优个体以一定概率加入随机扰动的局部搜索算子，以便使其在当前最优个体附近快速寻找更好的个体。若发现更优的新个体，则再次对新个体进行局部搜索，直到新个体停止改进或概率条件不满足为止。之所以不采用确定性的加入，主要是为了保证种群的多样性，从而避免算法陷入局部最优。局部搜索算子公式定义如下：

式中：xbestj（t）表示第t代最优个体Xbest（t）的第j个分量；σ为局部搜索算子的一个参数，它决定了对最优个体Xbest（t）加入的局部随机扰动的大小，即决定了Xbest（t）后代的变化范围。可见参数σ对算法收敛有重要的作用。

自然界在演化过程中，通常都遵循这样的演化规律，随着演化代数的增加，种群会逐渐向最优解靠近，即最优解的发现是一个连续渐变的过程，很少会以突变的形式得到最优解。因此，在本文提出的算法中，随着演化代数的增加，局部搜索算子也以一种连续渐变的方式逐步缩减其随机扰动的幅度，即参数σ逐步缩小，从而实现算法的稳定收敛。

在种群均匀初始化过程中，每个个体都被均匀分布在自变量的一个区段内。在添加局部扰动时，设定对其扰动的范围不能超过这一区段的1/2，即σ≤interval/2，其中interval是种群中个体间的间隔距离。在算法演化过程中，对每一代种群都要根据当前种群中自变量的分布情况重新计算个体间的间隔。随着演化的进行，种群会逐渐向最优解靠拢，种群内个体间的间隔距离也会逐渐缩小，因此也就保证了局部搜索算子以连续渐变的方式逐渐缩减扰动幅度。

2.4算法描述

步骤1初始化算法参数。设置种群规模M，缩放因子F，交叉因子CR，最大进化代数T，执行局部搜索算子的概率P1等相关参数。

步骤2初始化种群。按2.2节中的方法对种群进行初始化，得到在自变量取值范围内均匀分布的初始种群，设置初始进化代数t=0。

步骤3变异操作。采用经典DE算法的rand/1变异策略对种群实行变异。

步骤4交叉、选择操作。采用文献［7］中的方法对种群进行交叉生成2个子代个体，然后再选择一个个体进入下一代种群。

步骤5设置扰动参数。重新计算当前种群中的个体间隔，以设置扰动参数σ。

步骤6局部搜索。对当前种群中的最优个体以概率P1执行局部搜索，直到新个体不再改进为止。

步骤7终止条件检验。若进化代数t已达最大迭代次数T或达到预设精度，则输出最优个体xbest（t）的结果f（xbest（t））并停止；否则，置t=t+1，转步骤3。

3　实验测试及结果分析

为验证本文算法的性能，将其与文献［5］中的算法进行对比测试。测试函数取文献［5］中给出的7个常用测试函数。其中，n为函数自变量的维数，n=30；S为自变量的取值范围，其中f1（x）～f3（x）以及f5（x）的取值范围为［-100，100］；f4（x）的取值范围为［-600，600］，f6（x）和f7（x）的取值范围为［-50，50］。

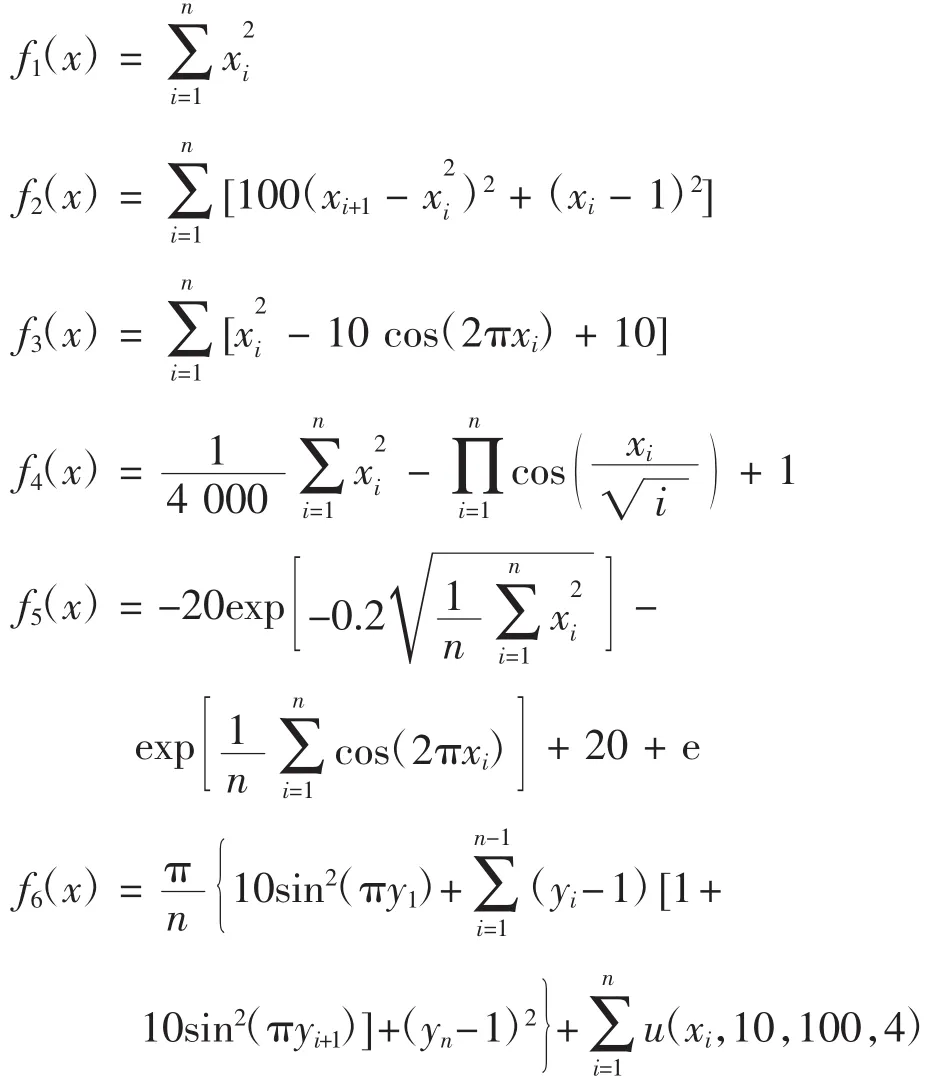
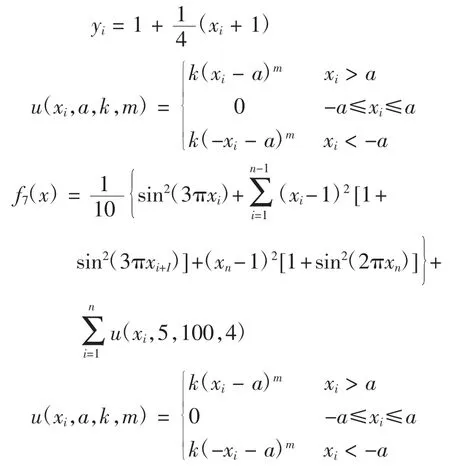
这些函数中，f1为单峰函数；f2为Rosenbrock函数，是一个非凸、病态单峰函数；其他函数为多峰函数；f2和f7在（1，1，…，1）处取最小值0，f6在（－1，－1，…，－1）处取最小值0，其他函数均在（0，0，…，0）处取最小值0。

为使结果具有可比性，所有测试函数取值范围、维数均与相应文献中取值相同。本文算法中交叉因子CR取0.9，缩放因子F取0.5，局部搜索概率P1动态取值并随演化代数逐渐增加。本文算法与文献［5］算法在7个测试函数上的对比实验结果如表1所示。

由表1可知，在函数f2、f3和f4上，本文算法和文献［5］算法一样每次都能找到全局最优解，算法表现十

表1　30维函数独立优化50次的实验结果

分稳定。除在f3上平均评价次数稍大些外，本文算法在f2和f4上的平均评价次数都远小于文献［5］中的算法，说明本文算法具有很好的收敛性能。对于函数f1，本文算法的求解精度也远高于文献［5］，且最优解的方差达到10-97，说明算法相当稳定；算法平均评价次数相对较小，也说明算法收敛较快。对于函数f5，本文算法虽然未能找到全局最优解，但从平均最优解质量来看仍然优于文献［5］，平均评价次数也略少于文献［5］。对于函数f6和f7，2种算法都未能找到全局最优解，但在得到相同最优结果的情况下，本文算法的平均评价次数远少于文献［5］的算法。综合来看，本文算法在测试函数上的表现要优于文献［5］，特别是在平均评价次数即收敛速度上是令人满意的。

4　结束语

本文算法在双子代竞争差异演化算法的基础上加入了局部搜索算子，并采用一定策略保证了初始种群在求解空间中的均匀分布，这使算法具有较强的搜索能力和较好的收敛性能。对7个经典benchmark函数的测试结果表明：该算法在最优解质量、平均进化代数和平均评价次数上都优于或至少不输于文献［5］的算法，同时该算法也具有很好的稳定性。

［1］STORN R，PRICE K.Differential evolution-A simple and efficient adaptive scheme for global optimization over continuous spaces［C］//International Computer Science Institute，California：Berkely，1995.

［2］PLAGIANAKOS V P，VRAHATIS M N.Parallel evolutionary training algorithms for“hardware friendly”neural networks［J］.Natural Computing，2002（1）：307-322.

［3］CHAKRABORTY U K，DAS S，KONAR A.Differential evolution with local neighborhood［C］//IEEE Congress on Evolutionary Computation CEC2006.Vancouver：IEEE Press，2006：2042-2049.

［4］何兵，车林仙，刘初升.双种群差分进化规划算法［J］.计算机工程与应用，2012，48（26）：25-31.

［5］刘进，覃洁萍.带惯性变异与正交设计的差分进化改进算法［J］.计算机工程与应用，2011，47（34）：34-38.

［6］姜立强，刘光斌，郭铮.分工差分进化算法［J］.小型微型计算机系统，2009，30（7）：1302-1304.

［7］武志峰，黄厚宽，张莹.基于Boltzmann机制的双子代竞争差异演化算法［J］.南京大学学报，2008，44（2）：195-203.

［8］张伟，刘三阳.动态局部搜索差分进化算法［J］.西南大学学报：自然科学版，2015，37（3）：93-98.

［9］欧阳海滨，高立群，孔祥勇．随机变异差分进化算法［J］.东北大学学报：自然科学版，2013，34（3）：330-334.

An improved differential evolution algorithm with local search operator

WU Zhi-feng，LIU Shuo，LI Yao-hui
（School of Information Technology and Engineering，Tianjin University of Technology and Education，Tianjin 300222，China）

As a particular instance of EA，although differential evolution algorithm is simple and powerful for optimizing continuous functions，it is still faced with premature convergence and easy getting in local optimization problems.In order to solve these problems，an improved differential evolution algorithm with local search operator is presented in this paper.For increasing colony diversity，the population is initialized by an uniform distribution.A local stochastic disturbance term is taken to the best individual of the population in each iteration with a probability.It can search a new individual with better fitness nearby the current individual and speed up the convergence.The experiments on seven common test functions show that this proposed algorithm is superior to the other algorithm on the quality of solution，average evaluation number and convergence speed.

differential evolution algorithm；local search；global optimization

TP301.6

A

2095－0926（2015）04－0001－04

2015-07-16

天津市应用基础与前沿技术研究计划（14JCYBJC15400）；天津职业技术师范大学人才计划资助项目（RC14-51）.

武志峰（1974—），男，教授，博士，硕士生导师，研究方向为演化计算、数据挖掘与知识发现.