RC框架结构地震倒塌易损性分析的实用方法1

党王桢 梁兴文

（西安建筑科技大学 土木工程学院，西安 710055）

RC框架结构地震倒塌易损性分析的实用方法1

党王桢 梁兴文

（西安建筑科技大学 土木工程学院，西安 710055）

基于增量动力分析（IDA）的倒塌易损性分析方法是评估建筑结构抗地震倒塌能力的精细方法，但分析过程比较繁杂且非常费时。为了较快地评估建筑结构的抗地震倒塌能力，首先利用静力非线性（pushover）分析，获得结构倒塌能力的初步估计值Sa*，然后将每个地面运动记录调整到Sa*，对结构进行动力时程分析，记录结构的动力时程反应，利用IDA的思想得到结构的中值数倒塌谱强度S˜CT。该方法与传统的增量动力分析方法相比较，可提高计算效率，计算精度也满足要求。

IDA 地震动记录 中值数倒塌谱强度˜SCT倒塌易损性曲线

党王桢，梁兴文，2015.RC框架结构地震倒塌易损性分析的实用方法.震灾防御技术，10（4）：986—995. doi：10.11899/zzfy20150417

引言

地震易损性分析是指在某一区域内，结构在不同强度水平地震作用下发生各种不同程度破坏状态的概率，是从概率的意义定量地刻画结构的抗震性能，从宏观角度描述地震动强度与结构破坏程度之间的关系。

最初，地震易损性被用于评估核电站的地震概率风险，随着易损性理论的快速发展，一些学者将其应用于变电站、古塔、混凝土重力坝、桥梁等一些重大结构的地震概率风险研究中。例如：Yamaguchi（1997）对核反应堆的管道系统进行了地震易损性研究，取得了很好的效果；清华大学的刘晶波与美国的Hwang等（2004）合作，对钢筋混凝土桥梁结构的地震易损性做了很多研究，给出了一种地震作用下钢筋混凝土桥梁结构易损性曲线的系统性分析方法；Bhargava等（2005）和Kapilesh等（2002）对核电站中的贮水罐进行了易损性评定。早期，国内外诸多研究者对普通建筑结构也开展了大量的研究工作。例如：Hwang等（1990a；1990b）很早就对RC框架结构、钢框架结构等的地震易损性进行了分析。尹之潜等（1996；2003）通过大量的震害调查和试验数据，建立了结构破坏状态与超越强度概率和延伸率的关系，并针对砖砌体房屋、厂房的排架结构以及多层钢筋混凝土结构进行了系统的地震易损性研究，形成了一整套关于结构易损性、地震危险性和地震损失估计的理论，建立了一种求普通结构易损性的简易方法。陆新征等（2011a；2011b；2009）对基于IDA方法的倒塌易损性进行了研究，通过倒塌易损性曲线对结构抗倒塌能力进行了评估。李谦（2011）对型钢混凝土框架结构基于IDA方法进行了研究，并把IDA方法应用到了型钢混凝土框架结构的地震易损性分析中。Schotanus（2004）研究了三维钢筋混凝土框架结构的地震易损性。

近年来，基于IDA分析方法的地震易损性研究已成为结构抗震设计研究的热点。但由于IDA方法整个分析过程繁杂费时，给评估工作带来很多不便。基于IDA的思想，本文首先利用静力非线性（pushover）分析，获得结构的倒塌能力的初步估计值Sa*，然后将每个地面运动记录调整到Sa*，对结构进行非线性动力分析，记录结构的动力时程反应，简便快速地得到结构的易损性曲线，进行结构的抗震性能评估。

1 基于IDA方法的地震易损性分析的基本原理和方法

1.1 IDA方法的基本原理

增量动力时程分析（IDA）方法是基于非线性动力分析提出的，是指对某一结构输入一条或多条地震动记录，通过设定一系列单调递增的比例系数SF（Scale Factor）对每条地震动记录进行调整，得到不同的地震动强度。并对结构在每个地震动强度作用下进行弹塑性时程分析，记录结构的弹塑性地震响应，从而产生一条或多条结构损伤（DM，Damage Measures）和地震动强度（IM，Intensity Measures）之间的关系曲线，即IDA曲线。增量动力时程分析（IDA）一般有多条IDA曲线，每条IDA曲线上的每个点代表结构在某一地震波的某一强度下的峰值反应，而一条曲线则代表一条地震动记录下结构的反应。

1.2 地震易损性分析的基本原理

地震易损性分析是指在某一区域内，结构在不同强度水平地震作用下发生各种不同程度破坏状态的概率。通常易损性曲线是以地震动强度为自变量，建筑物破坏概率为因变量的曲线。根据IDA的分析结果，可以得到结构的地震易损性曲线。

研究表明，结构反应的概率函数可用对数正态分布函数表示（龚思礼，2003），该函数可由中值数倒塌谱强度S˜CT与标准差β两个参数确定，βRTR为与地震动相关的不确定系数

RTR（0.20—0.40），反映了地震波的变异性。采用IDA方法确定结构的易损性曲线理论上非常简单，但对于大多数结构模型而言，实际完成一个IDA分析，得到一条几乎连续完整的IDA曲线，需要花费大量时间，同时还需耗费大量的人员和精力进行分析和处理数据。本文采用增量动力分析思想与下述简化方法（Liel等，2010）得到结构的倒塌易损性曲线：

（1）用静力非线性方法获得结构倒塌能力的初步估计Sa*。

（2）在规定的谱加速度水平评估倒塌概率。

在第1步获得结构倒塌能力的初步估计Sa*后，将每个地面运动记录调整到Sa*，对结构进行动力时程分析，以得到结构的动力时程反应。记录结构反应的关键指标，包括峰值层间侧移角、结构是否倒塌等。根据引起倒塌的地面运动记录数与总地面运动记录数之比，确定倒塌概率。

（3）修改第2步所得的结构倒塌能力。

如果第2步所得的倒塌概率大于50%，表明相应的谱强度值大于均值强度，则谱强度应修改为：

如果第2步所得的倒塌概率小于50%，表明相应的谱强度值小于均值强度，则谱强度应修改为：

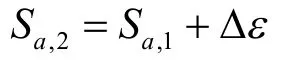
式中，Δε表示谱强度的步长。

（4）更新地面运动记录，进行动力时程分析。

获得了修改的倒塌能力估计值后，有可能减少需要运行的地面运动记录，需要进一步改进计算效率。如果一个特定的地面运动记录在Sa（ T1）=X处引起结构倒塌，则相同的地面运动记录将在任何Sa（ T1）＞X时引起结构倒塌。因此，如果修改的谱强度Sa（ T1）＞X，则该谱强度将引起结构倒塌，不需对该谱强度进行分析。相反，如果一个特定的地面运动记录在Sa（ T1）=X处不引起结构倒塌，则相同的地面运动记录将在任何Sa（ T1）＜X时不引起结构倒塌。

（5）重复第2、4步，直至结构倒塌。

对于每个新的谱强度值Sa，i，重复第2、4步。所有更新后的地面运动记录被调整为Sa，i，并进行动力时程分析。在每个Sa，i水平，进行时程分析，计算倒塌概率。

1.3 地震动的选取

FEMA P695（FEMA，2009）提供了两组地震波用于倒塌概率评估，分别为远场地震动记录与近场地震动记录。远场地震波组包括22组水平地震波，与场地距离不小于10km；近场地震记录包括28组水平地震波，与场地距离小于10km，这些地震记录均不包括竖向地震分量。远场地震动用于评估结构在B、C、D地震分组下的倒塌，近场地震记录仅用于对特殊结构或对E类地震分组结构的研究。

本文选用一个6层钢筋混凝土框架结构模型，处于Ⅱ类场地，根罗开海等（2006）的相关研究，美国现行规范（IBC，2009）中的C、D类场地大致对应我国Ⅱ类场地，采用FEMA P695报告推荐的22组远场地震动（共44条水平分量）作为IDA分析的地震动输入，详细信息见表1。

表1 地震动集合信息Table 1 Information about strong ground motion

续表

表1所选的天然地震动记录中的峰值加速度均符合我国《建筑抗震设计规范》（GB 50011-2010）中对时程分析所用地震加速度的最大值的要求，不需对其峰值加速度进行调整。

1.4 地震动强度指标和结构损伤指标的确定

IDA方法的结果通常用IDA曲线体现，而IDA曲线需要通过地震动强度指标（IM）和结构的损伤指标（DM）来描述，用以说明结构的地震响应随地震动作用的增强而变化的趋势。现有的地震动强度指标大致可以分为三类：第一类以PGA为代表；第二类以PGV为代表，包括PGV、阻尼比为5%的结构基本周期对应的加速度谱值Sa（T1，5%）等；第三类以PGD为代表。目前很多国家采用传统的PGA作为地震动强度指标，但近年来的各种研究分析和震害经验表明，将PGA作为地震动强度指标很不完善（Fajfar等，1990；李英民等，2001）。Neumann的研究（郝敏等，2005）认为，用PGV比PGA更能体现地震动强度等级；Vamvatsikos的研究结果（叶列平等，2009）表明，Sa（T1，5%）的离散性小于PGA的离散性，对弹性结构而言，在结构中长周期范围内，与结构响应的相关性较高，对弹塑性结构，在结构全周期范围内都有较高的相关性，目前日本就以PGV作为地震动强度指标。而PGD指标用的较少。

常见的结构损伤指标有：最大基底剪力、最大楼层延性、顶点最大位移θroof、最大层间位移角θmax等。结构损伤指标的选取与分析目的和结构特性相关，由于层间位移角反映了结构的层间位移延性和整体位移延性等，通过对层间位移角的分析可以全面了解结构的性能，故一般选用楼层最大层间位移角θmax。综上所述，本文对结构体系进行增量动力分析时，采用Sa（T1，5%）作为地震动强度指标，θmax作为结构损伤指标。

1.5 极限状态定义

本文在确定极限性能点时采用FEMA 350推荐的准则（FEMA，2000）：通过IDA曲线上的某一点来定义结构的极限状态点，这个点可清楚地将IDA分为倒塌区和非倒塌区。FEMA 350中定义，以20%的初始斜率和层间位移角为10%的点中对应IM值较小的点作为倒塌极限点。

2 RC框架结构非线性有限元建模

2.1 工程概况

本文所选结构模型为某一学生宿舍楼，位于抗震设防烈度7度（0.15g）地区，设计地震分组为第一组，场地类别为Ⅱ类。该建筑按现行抗震设计规范（《建筑抗震设计规范》（GB 50011-2010））设计。本文仅对该建筑的横向抗地震倒塌能力进行分析。

结构模型为6层RC规则框架结构，结构平面布置简图（未注楼梯间位置）见图1。总高度22.01m，首层层高为4.01m，二层及以上层高均为3.6m。材料参数：C35混凝土，梁、柱纵向钢筋以及箍筋均为HRB400，钢筋弹性模量Es=2×105N/mm2，屈服强度标准值400N/mm2。梁的截面尺寸均为300mm×600mm，梁、柱截面配筋如表2所示，表中梁截面配筋面积为受拉、受压区面积之和；柱截面配筋面积为全部钢筋面积之和。楼面恒载标准值为4.5kN/m2，活荷载标准值为2.0kN/m2。由于该结构力学模型在平面和立面上均对称，故建模时将空间框架模型简化为平面框架模型，选取整个结构的一半进行建模分析，楼层重量按照恒荷载+0.5活荷载计算。

图1 RC框架结构平面布置图Fig. 1 Floor plan of RC frame structure

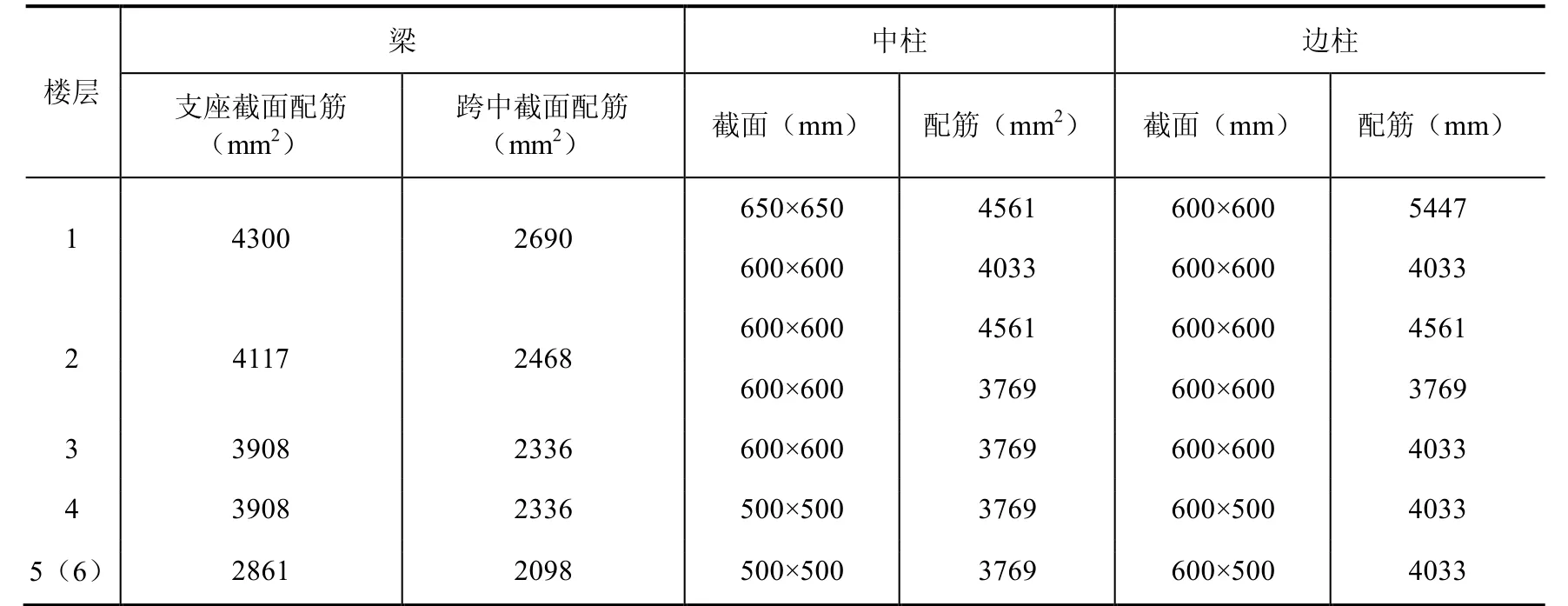
表2 结构模型截面参数Table 2 Section parameters of the structural model

2.2 非线性有限元建模

本文采用ETABS软件建模，采用PERFORM-3D软件进行结构动力非线性分析。PERFORM-3D软件提供了多种单元分析模型，为了准确地模拟梁、柱的应力、应变反应，梁、柱截面选用纤维截面模型，梁采用分布塑性区单元，柱采用集中塑性铰单元。

3 IDA分析

IDA分析过程需要对地震动记录进行调整，调整幅度用调幅系数SF表示，以表1所示1#地震动记录为例说明IDA分析过程中地震动记录的调幅。由PERFORM-3D软件求出该结构模型的基本自振周期T1=1.116s ，由反应谱可查出T1对应的阻尼比为5%的反应加速度Sa（ T1，5%）=0.8802g ，根据Vamvatsikos等（2002）建议的计算法则，调幅步长取0.2g，步长增量取0.05g，由Pushover曲线（图2）初步估计结构模型的Sa*=1.38g，调幅系数SF=1.38/0.8802=1.568，将每条初始地震记录的加速度乘以调幅系数SF得到第一次输入的加速度a1，然后把a1作为地震动输入，依次对结构进行非线性动力分析，可得到在地震动加速度a1激励下作用结构的最大层间位移角θmax。按照第一次的分析方法，可得到每次调幅后的最大层间位移角，直到层间位移角θmax数值发散，停止调幅。IDA的调幅过程如表3所示。

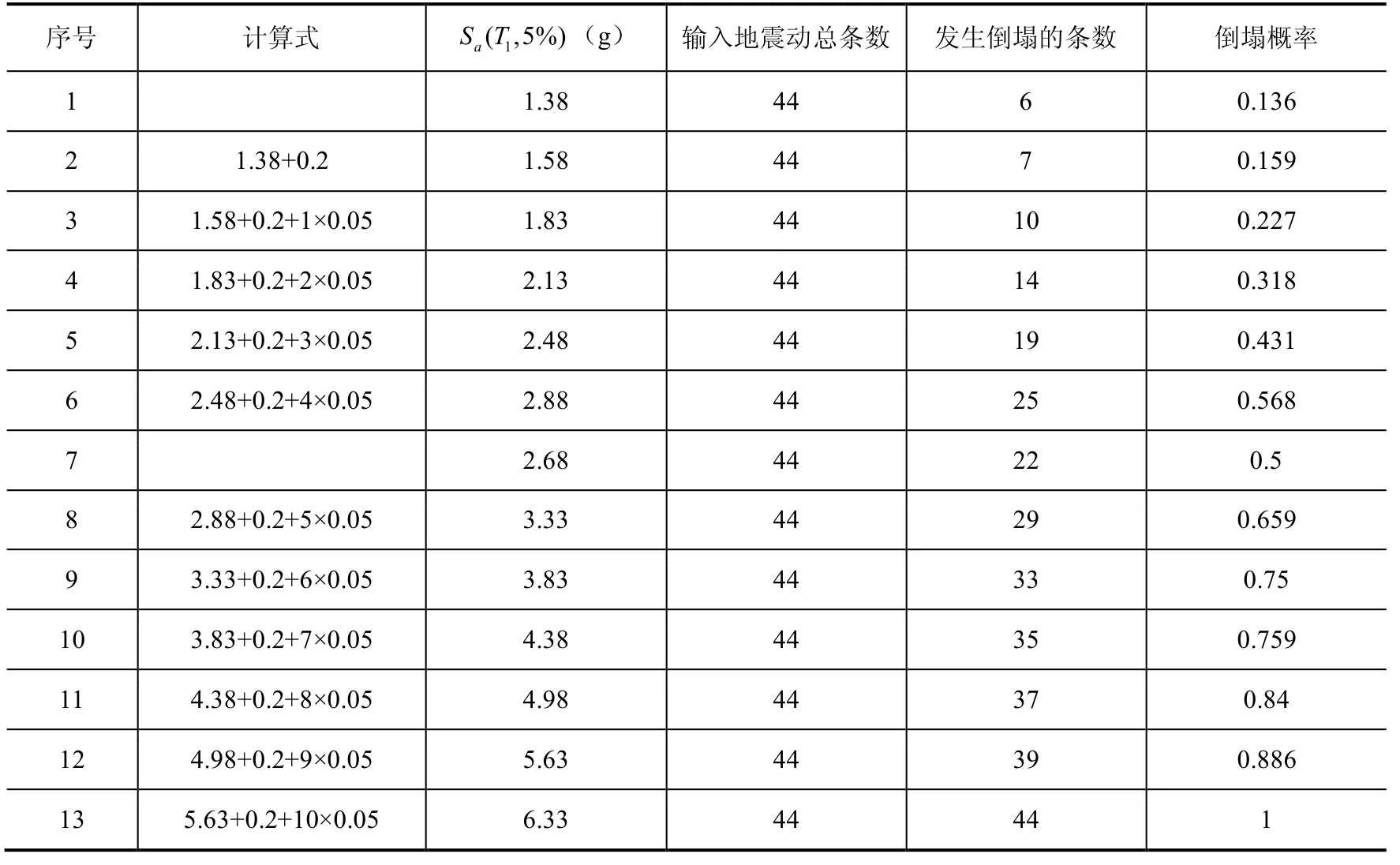
表3 地震动记录调幅（Sa（ T1，5%））Table 3 The adjustment about ground motion records

分析过程中，调整一次，平均每条地震动记录用时0.5小时，44条地震动记录用时22小时左右，得到图3所示的完整IDA曲线，少则需要调整10次，整个分析过程历时10天。图3为对结构模型输入44条地震动记录所得到的IDA分析结果。

图2 静力非线性分析曲线Fig. 2 Nonlinear static analysis curve

图3 44条地震动记录的IDA曲线Fig. 3 IDA response plots of 44 ground motion records

图4 基本模型的线性回归分析Fig. 4 Linear regression analysis of the model

4 易损性曲线的确定

4.1 基于实用方法倒塌易损性曲线的确定

汇总分析结果，将地震动强度与结构倒塌概率相联系，可以得到地震倒塌易损性曲线。图5为根据表3的IDA结果得到的结构倒塌易损性曲线。

4.2 基于IDA分析的倒塌易损性曲线的确定

假设地震需求参数的中值数D˜和地震动参数服从指数关系，即D˜=a（ S（ T，5%））b，两

a1边取对数则为：

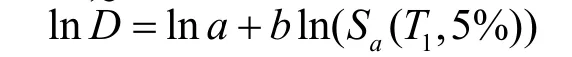
以地震动强度指标Sa的对数为自变量，结构损伤指标θmax的对数为因变量，对增量动力分析（IDA）的结果进行线性回归分析，结果图4所示。

地震概率需求模型的数学表达式为：

则A=lna=-3.61561，a=0.0269，b=B=0.95307，以Sa（ T1，5%）为自变量的结构倒塌概率计算公式为：其中，βRTR可取为定值0.4。将不同强度的Sa代入上式即可得到结构的地震倒塌易损性曲线（图6）。

从图5和图6可以看出，结构从完好状态发展到倒塌状态，易损性曲线逐渐平缓。当有一半的地震动记录发生倒塌时，由实用方法确定的结构的中值数倒塌谱强度Sa（ T1，5%）=2.68g，由传统的IDA分析确定的结构的中值数倒塌谱强度Sa（ T1，5%）=2.73g 。且由图7可以看出，两种方法得到的结构的倒塌易损性曲线较为接近，差异较小。

图5 基于实用方法的倒塌易损性曲线Fig.5 Collapse fragility curve of practical method

图6 基于IDA分析的倒塌易损性曲线Fig. 6 Collapse fragility curve of IDA analysis

图7 两种方法的倒塌易损性曲线对比图Fig. 7 The comparison curve of collapse fragility

5 结论

通过对6层钢筋混凝土框架结构地震易损性分析，可得出以下结论：

（1）用IDA分析得到的结构的中值数倒塌谱强度Sa（ T1，5%）=2.73g ，实用方法得到的结构的中值数倒塌谱强度Sa（ T1，5%）=2.68g，两者相比较，实用方法误差为1.8%，但用时节省了近90%。

（2）通过算例的计算，说明本文方法可应用于钢筋混凝土框架结构，是否还可应用于其他更为复杂的建筑结构，如剪力墙结构、框架-剪力墙结构等，还有待于进一步研究。

龚思礼，2003.建筑抗震设计手册（第二版）.北京：中国建筑工业出版社.

郝敏，谢礼立，徐龙军，2005.关于地震烈度物理标准研究的若干思考.地震学报，27（2）：230—234.

Hwang H.，刘晶波，2004.地震作用下钢筋混凝土桥梁结构易损性分析.土木工程学报，37（6）：47—51.

李英民，丁文龙，黄宗明，2001.地震动幅值特性参数的工程适用性研究.重庆建筑大学学报，23（6）：16—21.

陆新征，施炜，张万开等，2011a.三维地震动输入对IDA倒塌易损性分析的影响.工程抗震与加固改造，33（6）：1—7.

陆新征，唐代远，叶列平等，2011b.我国7度设防等跨RC框架抗地震倒塌能力研究.地震工程与工程振动，31（5）：13—20.

陆新征，叶列平，廖志伟，2009.建筑抗震弹塑性分析.北京：中国建筑工业出版社.

李谦，2011.增量动力分析方法的研究及其应用.西安：西安建筑科技大学.

罗开海，王亚勇，2006.中美欧抗震设计规范地震动参数换算关系的研究.建筑结构，36（8）：103—107.

尹之潜，1996.结构易损性分类和未来地震灾害评估.中国地震，12（l）：49—55.

尹之潜，赵直，杨淑文，2003.建筑物易损性和地震损失与地震加速度谱值的关系（上）.地震工程与工程振动，23（4）：195—200.

叶列平，马千里，廖志伟，2009.结构抗震分析用地震动强度指标的研究.地震工程与工程振动，29（4）：9—21.

Bhargava K.， Ghosh A.K.， Ramanujama S.， 2005. Seismic response and fragility analysis of a water storage structure. Nuclear Engineering and Design， 235: 1481—1501.

Fajfar P.， Vidic T.， Fischinger M.， 1990. A measure dynamics of earthquake motion capacity to damage medium-period structures. Soil Dynamics and Earthquake Engineering， 9 （5）: 236—242.

Federal Emergency Management Agency （FEMA）， 2000. Recommened Seismic Design Criteria for New Steel Moment-Frame Buildings. SAC Joint Venture， Washington DC: FEMA 350.

Federal Emergency Management Agency （FEMA）， 2009. Quantification of building seismic performance factors. FEMA P695. Washington DC: Federal Emergency Management Agency.

Hwang H.H.M.， Low Y.K， 1990a. Seismic reliability analysis of flat-plate structures. Probabilistic Engineering Mechanics， 5 （l）: 2—8.

Hwang H.H.M.， Jaw J.W.， 1990b. Probabilistic damage analysis of structures. Journal of Structural Engineering，ASCE， 116 （7）: 1992—2007.

International Building Code （IBC）， 2009. Country Club Hills， IL: International Code Council.

Kapilesh B.， 2002. Evaluation of seismic fragility of structures—a case study. Nuclear Engineering and Design，212: 253—272.

Liel A.， Tuwair H， 2010. A Practical approach for assessing structural resistance to earthquake-induced collapse. 19th Analysis & Computation Specialty Conference， ASCE.

Vamvatsikos D.， Cornell C.A.， 2002. Incremental Dynamic Analysis. Earthquake Engineering and Structural Dynamics， 31 （3）: 491—514.

Schotanus L.J.， 2004. Seismic fragility analysis of 3D structures. Structural Safety， 26 （4）: 421—441.

Yamaguchi A.， 1997. Seismic failure probability evaluation of redundant fast breader reactor piping system by probabilistic structural response analysis. Nuclear Engineering and Design， 195: 237—245.

The Practical Method of Collapse Fragility Analysis of RC Frame Structure

Dang Wangzhen and Liang Xingwen

（School of Civil Engineering， Xi’an University of Architecture and Technology， Xi’an 710055， China）

Collapse fragility analysis method based on the incremental dynamic analysis （IDA） is a fine algorithm of estimating structural resistance to earthquake-induced collapse. However， the analysis process is complicated and very time-consuming. In order to assess earthquake-induced collapse of structural resistance ability quickly， we suggest firstly utilizing nonlinear static （pushover） analysis to obtain an initial estimate） of collapse resistance，then adjust each intensity of ground motions records to， perform the dynamic time-history analysis and record the dynamic time-history response of the structure to receive the average spectrum intensityby the thinking of IDA. The proposed algorithm is more computationally efficient than a standard incremental dynamic analysis approach. The accuracy of the proposed approach also meets requirements.

IDA；Ground motions records；The median spectral intensity；Collapse fragility curve

国家自然科学基金项目（51278402）

2015-01-19

党王桢，女，生于1987年。硕士研究生。主要从事建筑结构及抗震研究。E-mall：ailianka0802@1025@163.com

梁兴文，男，生于1952年。教授，博士生导师。主要从事建筑结构及抗震研究。E-mall：liangxingwen2000@163.com