三维地形中地震动的频域特征——以芦山地区为例1

蒋 涵 周 红 高孟潭

（中国地震局地球物理研究所，北京 100081）

三维地形中地震动的频域特征
——以芦山地区为例1

蒋 涵 周 红 高孟潭

（中国地震局地球物理研究所，北京 100081）

地形条件对局部震害分布有重要影响。本文选择地形起伏剧烈的芦山地区，采用三维谱元法模拟地震波传播。研究了该地区地震动的频谱特征。计算了测线上位于山顶和山谷的台站傅里叶频谱，并研究了各自的谱值和谱值比特征。分析结果表明：山顶包含了较高的频谱；山谷包含了较低的频谱；山顶上的频谱值高于山谷的频谱值；并且地形对水平分量的影响更大。同时，进一步从频谱中提取了峰值放大比和峰值频率2个参数，分析了其在芦山地形中的分布特征。结果显示，山顶对应了较大的峰值放大比和峰值频率，而山谷则对应了较低的峰值放大比和峰值频率。

地形效应 傅里叶谱值 谱值比 谱元法

蒋涵，周红，高孟潭，2015.三维地形中地震动的频域特征——以芦山地区为例.震灾防御技术，10（1）：59—67.doi：10.11899/ zzfy20150106

引言

人们很早就认识到地表的起伏会影响地震灾害的分布。在多次地震事件中，如1971年San Fernando earthquake（Boore，1972）、1985年Chile earthquake（Celebi，1987）和Athens earthquake（Athanasopoulos等，2001），研究者都发现了这种地形放大效应。地形效应不仅能造成地震动的局部放大，还会造成滑坡和岩崩等次生危害。

在地形效应的研究中，一个重要的内容就是研究地震动的频谱特征。而计算地震动的傅里叶谱值和谱值比则是最常用的方法。其中，一种计算谱值比的方法是由Borcherdt（1970）提出的，称为标准频谱比法（Standard Spectral Ratio，简称SSR）；另一种计算谱值比的方法是由Nakamura（1989）提出的，称为水平竖向谱值比法（Horizontal Vertical Spectral Ratio，简称HVSR）。前者常用于对距离较近的台站记录进行分析研究，而两者的区别在于参考台站上的地震记录是否可用。

通常来讲，记录到的地震动放大会比模拟的预测结果要高（Geli等，1988）。造成这种差异性的一个原因可能是由于未能找到“合适”的用于计算放大比例的参考台站（Pedersen等，1994）；另一个原因可能是记录到的放大效应往往是其他效应的综合（Bard等，1999；Paolucci，2002），比如：震源的方向性、速度界面的不规则性以及对局部地质条件认识的不充分等，特别是由速度界面起伏造成的放大，通常要比地形造成的放大大得多，从而掩盖了地形放大效应（Paolucci，2002）。因此，尽管强震观测记录很多，但真正能够很清楚地显示地形放大效应和放大量级的强震观测记录却很少。

本文利用数值法来研究由地形起伏造成的地震动放大的频域特征。使用基于谱元法构建的芦山地区三维计算模型，模拟了爆炸源产生的地震波的传播。并通过简单的介质和震源，突出地表起伏造成的地震动的放大。研究在三维地形中放大效应的频域特征。

1 芦山地区三维计算模型

谱元法是本文使用的数值方法，它属于谱方法中的一种。和有限元法一样，谱方法也源自经典的Galerkin法。谱方法的精髓在于它的形函数是由高阶的正交多项式表示的，这就使得其精度相对于低阶的有限元形函数有了极大的提高。谱方法最早使用的正交多项式为Chebyshev多项式（Patera，1984），后来则采用结合了Legendre-Gauss-Lobatto点的拉格朗日多项式（Faccioli等，1997；Komatitsch等，1998）。后者就是本文中所使用的谱元法（Spectral-Element Method）。在谱元法的弹性动力学变分公式中，自然地也加入了自由边界条件，因此被认为是谱方法中最适合研究弹性波问题的方法（Paolucci，2002）。

龙门山断裂带是青藏高原与扬子地台的接触带，是前者向后者挤压的结果。笔者选择的研究区域为龙门山南段的芦山地区，该地区的地形起伏剧烈，同时地震活动也较为频繁。谱元法的地表网格点由数字高程模型（Digital Elevation Model）构建，如图1所示。为了进一步突出纯粹由地形不规则产生的地震动放大效应，选择了较为简单的介质与震源模型；速度模型为水平分层结构，共有3层，从地表往下P波速度依次为4.0km/s、6.1km/s和6.3km/s。为了更好地研究地形效应，还构建了一个地表水平的模型，其地表海拔统一为1km，其余参数与第一个模型相同。震源由一个爆炸点源表示，使用ricker子波表示时间函数，子波的具体表达式为：

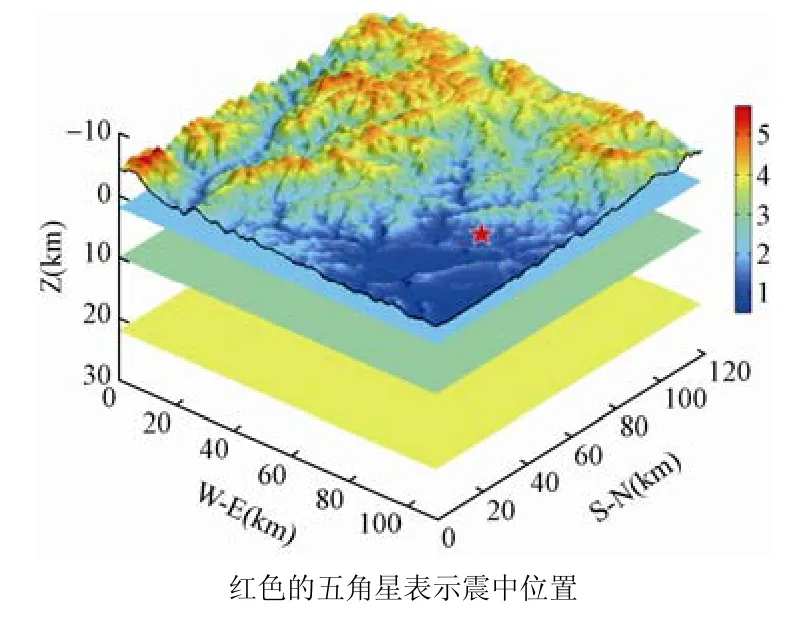
图1 芦山地区计算区域的三维示意图Fig. 1 The 3D computation area of Lushan Region

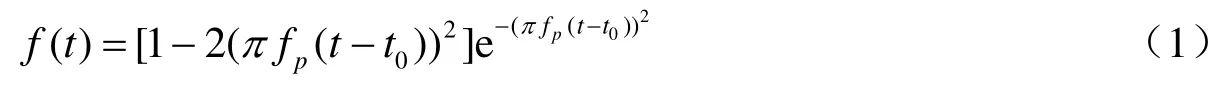
式中，fp为子波的主频，或者称之为峰值频率（peak frequency）；t0为时间延迟。峰值频率fp取1.5Hz，有效频段范围大致为0—3.0Hz。时间递推格式为显示的Newmark预测-校正格式，时间离散步长Δt为0.005s。

除了自由边界条件的地表以外，其他5个边界面用一阶次的Liao式投射边界（Liao等，1984）来防止地震波场的假反射。

2 地震动频谱特征

2.1 测线上的傅里叶谱值

在并行的环境中，笔者计算得到了地表的速度时程曲线。从地表上选择了5条具有代表性的测线，编号分别为：L1、L2、L3、L4、L5，它们自西向东等间距分布，与原点的距离分别为20km、40km、60km、80km、100km。在每1条测线上均选出12个位于山顶和12个位于山谷的接收点，如图2所示，台站的编号自西向东依次增加。首先通过傅里叶变换，求得每个接收点上的时程曲线对应的傅里叶频谱。同时为了研究地形对地震动谱值的影响，将12个山谷台站的谱值归一化，让其峰值都统一为单位1，并计算它们的均值。用同样的方法可得到12个山顶台站的均值，计算的结果如图3所示。

图2 5条测线上的地形起伏示意图Fig. 2 Illustration of topography on five profiles

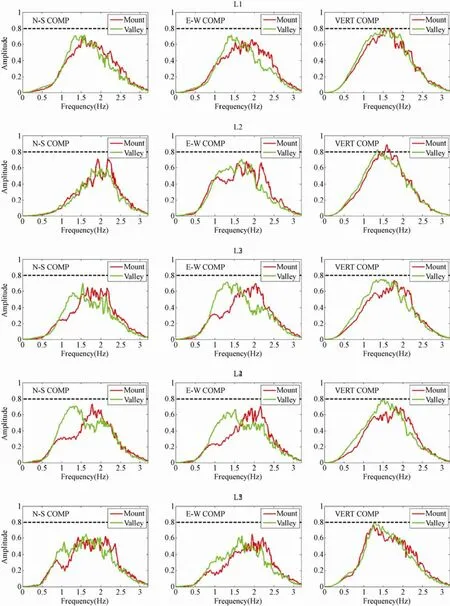
图3 5条测线上台站的傅里叶三分量频谱平均值Fig. 3 Fourier spectrum of stations on the five profiles

从图3中5条测线的结果可以看出，山顶谱均值（图3中的红线）和山谷谱均值（图3中的绿线）存在着明显的差异：山顶地震动的频谱中包含了更多的高频成分；而山谷地震动的频谱中包含了更多的低频成分；这表明山顶地形相对于山谷地形增加了地震动中的高频成分。从三个分量上来看，水平向上的山顶谱值与山谷谱值的差异更大；而在垂直向上两者的差异较小；这个特点表明地形对不同分量地震动的频谱成分的影响不同，对水平分量的影响更大。

2.2 测线上的傅里叶谱值比

上一节研究了山顶和山谷的地震动谱值特征。本节借鉴标准频谱比（SSR）的研究思路，把每个测线上的山谷台站作为对应相同编号的山顶台站的参考台站。按照地形放大函数（Topographical Amplification Function）的值等于山顶台站的谱值AM(v)和它的参考台站（山谷台站）的谱值AV(v)的比值（Celebi，1987），其表达式为：

为了减小地形放大函数中由震源和传播路径造成的影响，突出地形带来的幅值影响，将山顶和山谷的振幅谱都除以了对应的平层模型中谱值的最大值A＇( v)，加入修正项后的地形放大函数的表达式为：

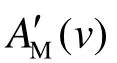
5条测线的计算结果如图4所示。每个测线的3个子图分别代表X方向、Y方向和Z方向上的地形放大函数，其中，纵坐标代表的幅值用对数坐标表示，横轴代表的频率范围为0—3.0Hz。图4中不同颜色的细线代表相应的单个地形放大函数，粗黑线表示的是12个放大函数的均值。

从图4可以看出，尽管单个放大函数曲线变化大，但均值却在不同测线上表现出了以下相似的特征：①除了一些极少数频段，山顶上的频谱值都大于山谷的频谱值。在一些频段上，谱值比可以达到7—8倍。②在水平分量上，从0.5—1.0Hz地形放大函数幅值逐步上升。在1.0—1.5Hz谱值则逐渐下降。在0.5—1.5Hz形成了一个大致的波峰轮廓。在1.5Hz以后，地形放大函数逐渐增加，并维持在较高的放大倍数水平上，同时还伴随着较剧烈的震荡。其放大倍数平均水平大致为4—5倍，最高可达到7—8倍。③对竖向分量而言，在1.5Hz频段之前，赋值平稳保持在1左右。这表明在0.5—1.5Hz频段上，竖向频谱受地形的作用比水平向要小。而在1.5Hz之后，竖向分量则和水平分量的形态较为接近，幅值比达到了较高倍数并伴有震荡。

2.3 峰值放大比和峰值频率在芦山地区的分布

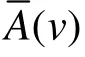
图4 5条测线上三个分量的地形放大系数Fig. 4 Topography amplification functions of three components on five profiles

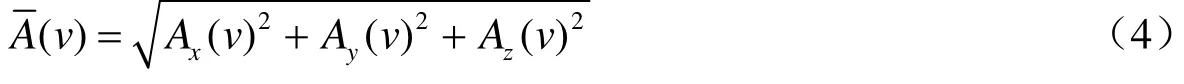
图5（a）峰值放大比在芦山地区的分布Fig. 5（a） Distribution of peak amplification ratio in Lushan area

图5（b）峰值频率在芦山地区的分布Fig. 5（b） Distribution of peak frequency in Lushan area

从图5（a）可以看出，比值R在山脊上普遍超过了1，而在某些山脊上甚至达到了2倍以上；同时，在山谷中的比值普遍小于1。同样地，峰值频率ν也表现出了类似的特点：在山顶上的时候，峰值频率会偏移到较高频率段，而在某些山脊上、尤其是某些宽度较窄的山脊上，峰值频率达到了2.2Hz以上；而在山谷中的时候，峰值频率则会迁移到较低频率段，比如在位于西南段的1条较深的峡谷中，峰值频率下降到了1.2Hz以下。

3 结语

本文从频域的角度对芦山地区的地形放大效应进行研究。选择了5条测线，并从每条测线上分别选出12个山顶台站和12个山谷台站，通过计算每个台站的谱值和山顶、山谷谱值比，研究了测线上的地震动频谱特点。随后，又从频谱中提取了放大比和峰值频率2个参数，研究了地震动频谱在三维芦山地形中的分布特征。其主要结论如下：

山顶和山谷地形对应的地震动频谱的高低频的比例不同，山顶地震动的谱值中包含了更多的高频成分；而相对应的山谷谱值则包含了更多的低频成分。地形对地震动不同分量的影响也不同，水平向上的山顶谱值与山谷谱值的差异更大。

在0—3.0Hz频谱范围内，山顶上的频谱值大于山谷的频谱值，在某些频段的峰值上可以达到7—8倍。地形放大函数在水平向和竖向上存在差异，在水平分量0.5—1.5Hz频段上，地形放大系数先升后降；在1.5Hz以后，地形放大系数增加，并维持在较高的放大倍数上，且伴有一定的震荡；在竖向分量上，在1.5Hz之前保持在1左右，而在1.5Hz之后，变化情况和水平向分量接近。

峰值放大比在山顶上超过1，在山谷中小于1。峰值频率也有类似特点，在山顶上峰值频率较高，尤其是在某些细小的山脊上峰值频率可达到2.2Hz；而对应的山谷峰值频率则较低。

Athanasopoulos G.A.，Pelekis P.C.，Xenaki V.C.，2001. Topography Effects in the Athens 1999 Earthquake：the Case of Hotel DEKELIA. See：Proceedings of the Fourth International Conference on Recent Advances in Geotechniques and Earthquake Engineering Soil Dynanics，San Diego，California，2001. Paper No. 10.42.

Bard P.Y.，Riepl-Thomas J.，1999. Wave propagation in complex geological structures and their effects on strong ground motion. In Wave Motion in Earthquake Engineering，Kausel E.，Manolis GD（eds.）. International Series Advances in Earthquake Engineering，WIT：Boston，37—95.

Boore D.M.，1972. A note on the effect of simple topography on seismic SH waves. Bulletin of the Seismological Society of America，62（1）：275—84.

Borcherdt R.D.，1970. Effects of local geology on ground motion near San Francisco Bay. Bulletin of the Seismological Society of America，60（1）：29—61.

Celebi M.，1987. Topographical and geological amplifications determined from strong-motion and aftershock records of the 3 March 1985 Chile earthquake. Bulletin of the Seismological Society of America，77（4）：1147—1167.

Faccioli E.，Maggio F.，Paolucci R. et al.，1997. 2D and 3D elastic wave propagation by a pseudo-spectral domain decomposition method. Journal of Seismology，1（3）：237—251.

Geli L.，Bard P.Y.，Jullien B.，1988. The effect of topography on earthquake ground motion：a review and new results. Bulletin of the Seismological Society of America，78：42—63.

Komatitsch D.，Vilotte J.P.，1998. The spectral element method：an efficient tool to simulate the seismic response of 2D and 3D geological structures. Bulletin of the Seismological Society of America，88（2）：368—392.

Liao Z.P.，Wong H.L.，Yang B.P. et al.，1984. A transmitting boundary for transient wave analysis. Scientia Sinica，27（10）：1063—1076.

Nakamura Y.，1989. A method for dynamic characteristics estimation of subsurface using microtremor on the ground surface. Railway Technical Research Institute，Quarterly Reports.

Paolucci R.，2002. Amplification of earthquake ground motion by steep topographic irregularities. Earthquake Engineering & Structural Dynamics，31（10）：1831—1853.

Patera A.T.，1984. A spectral element method for fluid dynamics：laminar flow in a channel expansion. Journal of Computational Physics，54（3）：468—488.

Pedersen H.，Le Brun B.，Hatzfeld D. et al.，1994. Ground motion amplitude across ridges. Bulletin of the Seismological Society of America，84：1786—1800.

The Characteristics of Frequency Domain of Ground Motion in 3-D Topography——A Case Study of Lushan Area

Jiang Han，Zhou Hong and Gao Mengtan
（Institute of Geophysics，China Earthquake Administration，Beijing 100081，China）

The topography plays an important role in local disaster distribution. In this article, Lushan area with steep topography is chosen as our research area. We use 3-D spectral element method to simulate seismic wave propagation and analyze the spectrum of strong ground motion. We calculate the spectrum of velocity time history of stations on ridge and valley of selected profiles. The results show that the spectrum on ridge contains higher frequency and spectrum on valley contains lower frequency. Spectrum on ridge are larger than spectrum on valley, and the surface irregularity has greater effect on horizontal components. Moreover, we calculate the peak amplification ratio and peak frequency from the spectrum and analyze their distribution on Lushan topography. The results show that the ridge has larger amplification ratio and peak frequency while the valley has lower ratio and peak frequency.

Topography effect；Fourier spectrum；Spectrum ratio；Spectral-element method

地震行业科研专项（201408014）和基本业务专项基金（DQIB14C02）资助

2014-06-22

蒋涵，男，生于1988年。硕士。主要研究方向：数值模拟。E-mail：jianghan 2013@gmail.com

周红，女，生于1969年。研究员。主要从事地震波理论与数值模拟研究。E-mail：zhouhong@cea-igp.ac.cn