一种振动能级梳状滤波精确计算方法
2015-10-24高慧中
孙 涛,高慧中
(中国船舶重工集团公司 第705研究所,陕西 西安,710075)
一种振动能级梳状滤波精确计算方法
孙涛,高慧中
(中国船舶重工集团公司 第705研究所,陕西 西安,710075)
现有的1/3倍频程处理方法都是以测试信号不包含明显干扰为前提,因而在处理带噪声信号时存在一定先天不足。针对现场测量信号中经常存在规律性噪声(噪声线谱呈梳状等间隔分布)的现象,提出了以Fourier核函数为基函数的梳状带阻滤波器与1/3倍频程有机结合来消除规律性噪声对结果影响的方法。该方法能够在频域下直接消除干扰并计算滤波后信号的振动能级,计算量小、精度高。通过对动力装置功率试验中出现规律性噪声的振动信号进行合理修正,重新评估其振级水平,避免了多次重复试验,节约了试验费用。
动力装置; 振动噪声; 信号处理; 1/3倍频程
0 引言
噪声作为人们不希望出现的声音,却大量的出现在人们的日常生活与生产活动中。在工业集中、人口密集的大中型城市,噪声严重危害人民群众的身心健康; 而在激烈的军事对抗中,潜艇、战机与军舰的噪声大小更直接与隐身性能直接相关,正是基于这样的原因,越来越多的学者对其加以研究以实现降噪。声音来源于振动,二者之间有很好的相关性,因而针对在工业现场难以使用测量仪器直接获取的噪声,通常采取“以振代噪”的方法进行评价。
倍频程方法是根据人耳对声音的响应特性构造的一种频域分析方法,具有谱线少、频带宽的特点,广泛应用于声学和振动的评估,并得到普遍认可[1]。一些学者从提高计算精度[2]、滤波器数字化[3]和增强处理功能[4]等方面对标准倍频程算法进行改进,大大推动了该方法的工程应用。在1/3倍频程方法的相关研究中,都是以测试信号为正常信号,不包含明显干扰为前提,因而在处理带噪声信号时存在一定程度的先天不足。
实际生产中,现场获得的振动信号往往包含由诸如齿轮、轴承等外部系统引起的等间隔频率成分,甚至不明干扰源引入的干扰谱线。如果不对这些干扰频率成分进行处理就直接计算振动能级,必然导致计算结果偏大,影响评判的准确性。尽管目前已有多种成熟的梳状滤波器构造方法[5-6],但不同的构造方法各具特点[7],尚无学者研究哪种梳状滤波器适合与1/3倍频程方法结合并实现它们的有机整合。
该文提出以Fourier核函数为基函数的梳状带阻滤波器与1/3倍频程有机结合来消除规律性噪声对结果影响的方法,并通过模拟数据与实测数据验证了该方法的可行性。
1 算法流程
目前的梳状滤波器通常采用Morlet小波作为基础单元来构造,这是因为Morlet小波作为高斯包络下的一个复指数函数,时域下收敛性好,可以通过改变其函数参数来改善边线下降速度,得到较为理想的窄带滤波器,获取某些特征频段,最终通过包络检波完成分析[8-9]。但是,Morlet小波在频域下呈现“钟”型曲线,顶部不平坦,且幅值一般不为1,并不能较好的满足梳状滤波需求[6]。因而,文中选择以Fourier核函数构建梳状滤波器,利用时域卷积等效于频域相乘的原理,将原始信号的功率谱和构造出的梳状带阻滤波器相乘,滤除原始信号中的周期性干扰成分,然后再通过滤波后的功率谱计算1/3倍频程谱,其简要流程如图1所示。该方法在频域下直接消除干扰并计算滤波后信号的振动能级,计算量小、精度高,可用于修正因干扰导致的振动能级误报。
Fourier核函数的定义如下

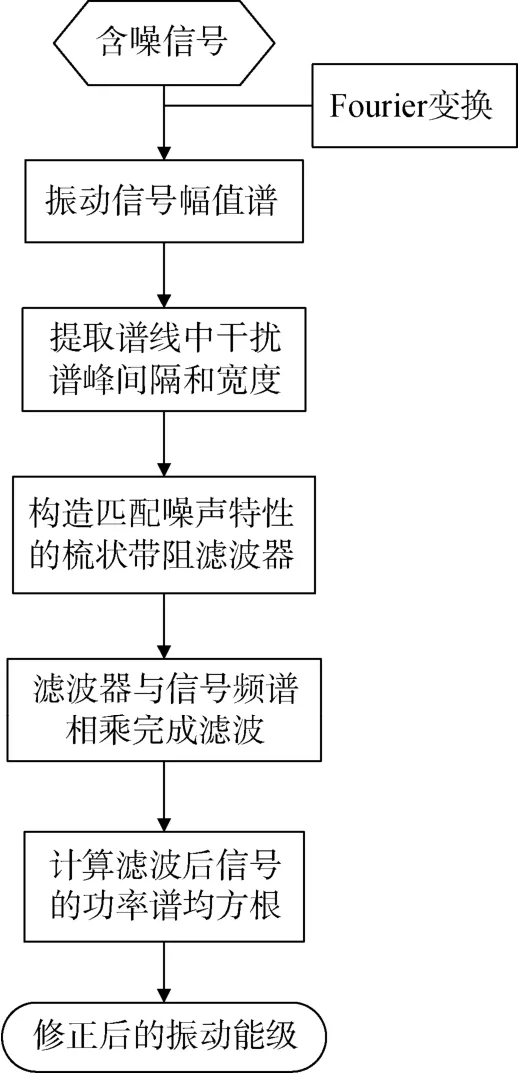
图1 消除梳状噪声影响的1/3倍频程方法流程图Fig. 1 Flow chart of 1/3 octave spectrum method for eliminating comb-noise
由于s(t)为自变量过零点的对称函数,若直接取t=0计算,无法获得正确的数值解,文中提出可使用极限方法求解,即
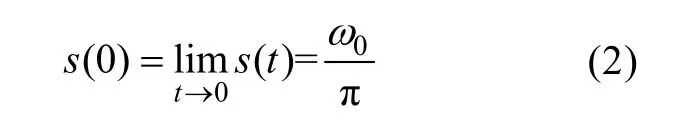
s(t)对应的频域分布特性为
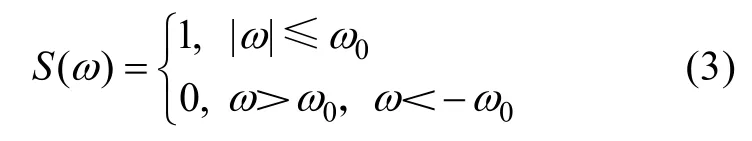
其中ω0≥0,表示所构造带通滤波器的截止频率,其频域分布特性曲线如图2所示,取ω0=2π。
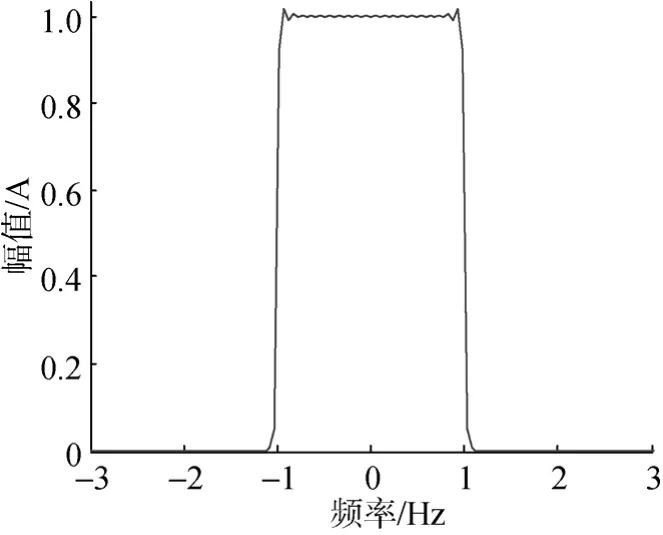
图2 Fourier核函数频域波形Fig. 2 Waveform of Fourier kernel function in frequency domain
可以看出,Fourier的频域特性曲线相当于一个幅值为1的平顶带通滤波器。根据Fourier变换的性质,通过设置频移因子可构造出由多个带通滤波器组成的基于Fourier核函数的梳状滤波器
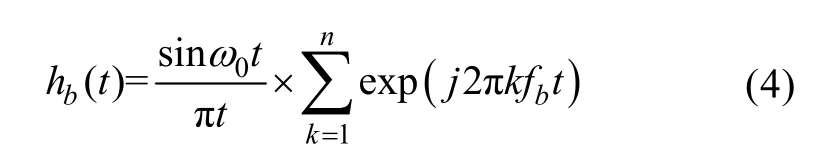
构造出的hb(t)是以fb为等间隔,通带带宽为2ω0的梳状滤波器,在频域下将只能通过频率为fb及其倍频成分,还无法满足滤除梳状干扰频率的要求,因此可在分析频率fa范围内构造一通频带通滤波器
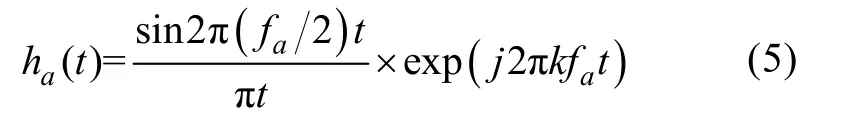
ha(t)的带宽将覆盖整个分析频率范围。
在此基础上,将构造得到的ha(t)与hb(t)进行Fourier变换得到Ha(ω)与Hb(ω)。根据Fourier变换的特性可知,梳状滤波器Hc(ω)=Ha(ω)-Hb(ω)的频域分布特性如图3所示。
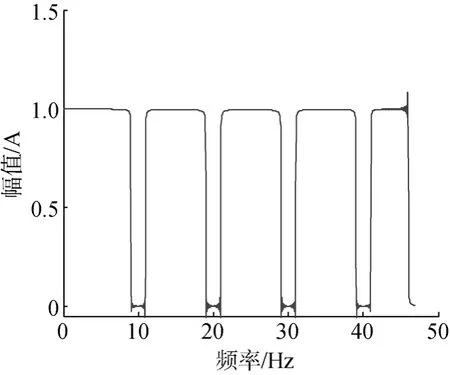
图3 梳状带阻滤波器频域分布Fig. 3 Frequency domain distribution of comb bandstop filter
Hc(ω)将仅对fb及其倍频产生带阻特性,而对其余频率成分具有带通特性。
对原始信号x(t)的频域值X(ω)进行梳状滤波,得到对应的频谱W(ω)后计算功率谱密度G(ω),其求解过程如下

由此得到在以fc为中心频率的第h个频段[fl,fu]内功率谱的平均值为
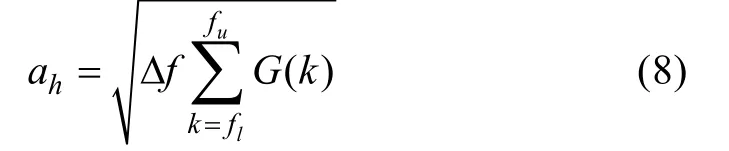
其中,n为频段内谱线个数。若以a0为零分贝基准值,则ah的能级可表示为
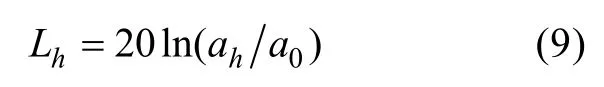
相比于原有滤波方法,此方法的滤波过程在频域下直接进行,形象直观,且得到的频域结果可直接计算功率谱,无需再次进行傅里叶变换,避免了误差的引入。
2 工程应用与仿真
2.1仿真测试
构造含有间隔为10 Hz的梳状谱噪声的模拟信号,其数学表达式为
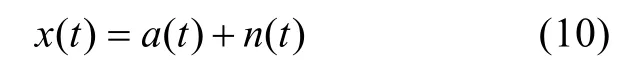
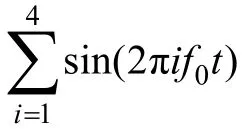
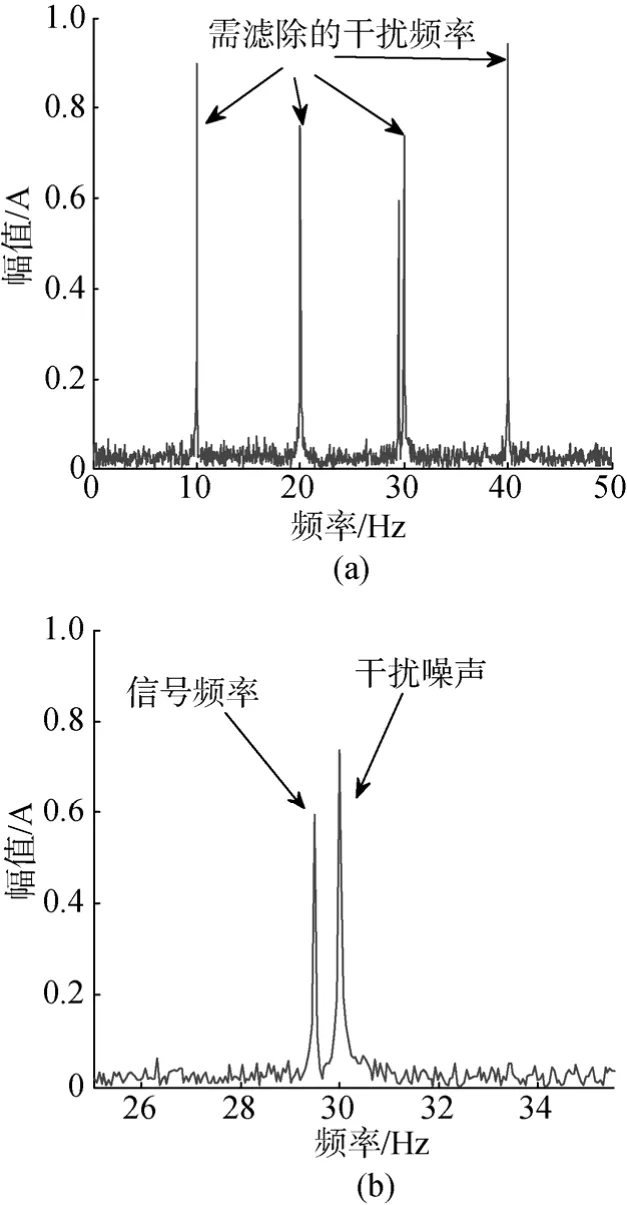
图4 模拟信号频谱分布Fig. 4 Frequency spectrum distribution of simulated signal
观察模拟信号的频谱X(ω)可以发现,10,20,30,40 Hz处分布有等间隔的谱线,且幅值远大于其余频段的数值。以Fourier核函数为基础,构造幅值为1中心频率fc=10,20,30,40 Hz,带宽B=2 Hz 的平顶带阻滤波器Hc(ω)。
在得到了梳状带阻滤波器的频谱Hc(ω)后,根据时域卷积等效于频域相乘的原理,滤波过程可直接在频域下完成,滤波后的结果如图5。

图5 滤波后的频谱分布Fig. 5 Frequency spectrum distribution of filtered signal
通过与图4对比可看出周期性干扰谱线得到了明显抑制,且其余频段信息得到了完整保留。根据国际电工委员会对1/3倍频程各频带范围的规定[10]可以确定,4根干扰谱线位于中心频率为10 Hz,20 Hz,31.5 Hz和40 Hz这4个1/3倍频程频带内。原始信号的振动能级L1与滤波后信号的振动能级L2对比见图6。为了便于观察,该图的1/3倍频程中心频率范围取为8~40 Hz。可以清晰地看到,干扰谱线所在频程的振动能级得到了显著抑制。需要注意的是,由于干扰信号的30 Hz谐波与有用信号的频率(29.5 Hz)十分接近,导致在滤波过程中有用信号也被滤除。针对这一问题,需要在密集分布区域单独设计滤波器带宽,避免有用信号被滤除。而对于更复杂的重合问题,可在预处理阶段选择更加有效的特征提取与分析技术对其加以分离,再完成滤波。
2.2工程验证
动力装置的功率试验是在陆上全面检验动力装置性能最有效的试验手段。振动是功率试验最重要的考核指标之一。受现场测试条件的限制,振动测量数据中不可避免地包含各种干扰。
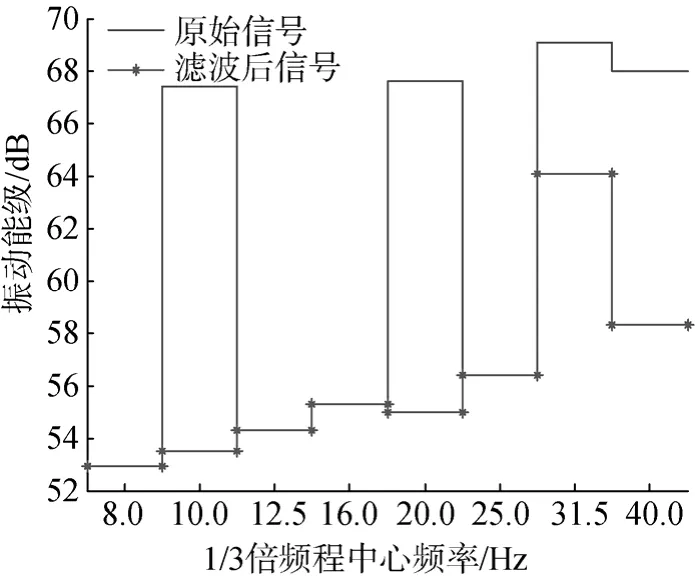
图6 仿真信号振动能级对比图Fig. 6 Contrast of vibration levels for simulated signal
在某阶段现场试验中,连续几次功率试验评估点振动信号都包含间隔约100 Hz的周期性干扰,如图7所示,并且干扰频率的时间间隔和幅值不随动力装置速制的变化而变化。动力装置机械运动激励频率等于发动机转频的分数倍或整数倍,当发动机的转频变化时,动力装置的机械运动激励频率必然随之变化。因此,判断评估点振动频谱的尖峰簇不是由动力装置组件的机械运动激励产生的,而是来自于外部干扰源。
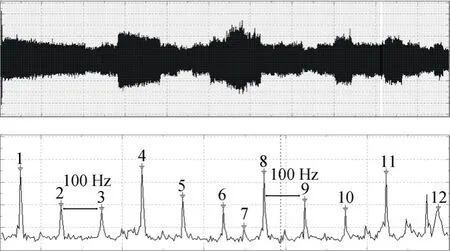
图7 实测信号的时域与频域曲线Fig. 7 Measured signal curves in time and frequency domains
采用消除梳状噪声影响的1/3倍频程方法,取带宽B=10 Hz,间隔fb=100 Hz的梳状滤波器对异常信号进行处理,滤波前后的振动能级曲线对比如图8所示(滤波仅对规律谱线集中出现的频段),可以看出,滤波后分贝值有所降低,符合振动要求(随后的湖试测噪也间接证明消除干扰噪声前振级超标的动力装置振动处于正常范围)。通过对功率试验中出现类似特征的振动信号进行合理修正重新评估其振级水平,避免了多次重复试验,节约了试验费用。
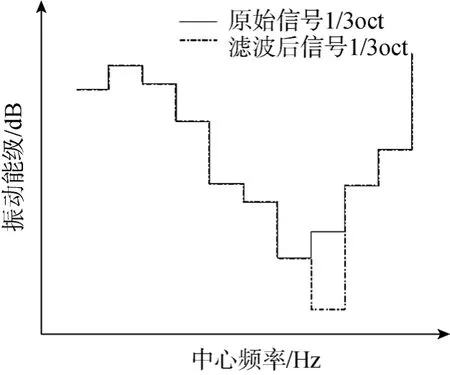
图8 实测信号振动能级对比图Fig. 8 Contrast of vibration levels for measured signal
3 结束语
随着人们生活品质追求的日益提高和军事对抗技术的不断进步,噪声的危害引起了主要工业部门的普遍关注。噪声测试与评估是噪声综合治理的前提,评估方法的先进程度直接影响评估的准确性和效率。本文针对现场测量信号中经常存在规律性噪声(噪声线谱呈梳状等间隔分布)的现象,将1/3倍频程技术与梳状带阻滤波构造技术有机结合,并在此基础上对求解过程加以优化,提高了求解效率。该方法已广泛应用于鱼雷动力装置及主要组件在复杂现场环境下的振动评估,大大提高了评估的准确性。
[1]孙涛,高爱军,王炜,等. 一种多测点变工况倍频程快速处理方法[J]. 鱼雷技术,2011,19(6): 455-458.
Sun Tao,Gao Ai-jun,Wang Yi,et al. A Fast CPB Processing Method of Off-design Vibration and Noise Data from Multiple Channels[J]. Torpedo Technology,2011,19(6): 455-458.
[2]成峰,周宝焜,程利青,等. 基于MATLAB的1/3倍频程FIR数字滤波器设计[J]. 福州大学学报(自然科学版),2003,31(2): 160-165.
Cheng Feng,Zhou Bao-kun,Cheng Li-qing,et al. Design of Third-Octave Band FIR Digital Filters Based on MATLAB[J]. Journal of Fuzhou University(Natural Science),2003,31(2): 160-165.
[3]Flink J H,Bertrand J. Specrrum Analyzer Using Digital Filters: US,747053[P]. 1976-12-3.
[4]孙涛,高爱军,李留成. 直接获得同工况比邻的多测点变工况倍频程谱阵的方法: 中国,ZL201110012751.1[P]. 2014-3-14.
[5]李志勇,危韧勇,张涛. 基于Morlet组合小波的梳状滤波与包络检波方法[J]. 中南大学学报(自然科学版),2006,37(2): 336-340.
Li Zhi-yong,Wei Ren-yong,Zhang Tao. A Comb-filter and Envelope-demodulation Method Based on Combined Morlet Wavelets[J]. Journal of Central South University(Science and Technology),2006,37(2): 336-340.
[6]赵俊龙,郭正刚,张志新,等. 梳状滤波器在滚动轴承早期故障诊断中的应用[J]. 振动与冲击,2008,27(12): 171-174.
Zhao Jun-long,Guo Zheng-gang,Zhang Zhi-xin,et al. Application of Comb Fil the in Fault Early Diagnosis of Rolling Element Bearing[J]. Journal of Vibration and Shock,2008,27(12): 171-174.
[7]侯者非,杨杰,王克成,等. 改进梳状包络检波方法在滚动轴承故障诊断中的应用[J]. 煤矿机械,2010,31(2): 229-232.
Hou Zhe-fei,Yang Jie,Wang Ke-cheng,et al. Novel Comb-filter and Envelope-demodulation Method Applied in Fault Diagnosis of Rolling Element Bearing[J]. Coal Mine Machinery,2010,31(2): 229-232.
[8]Bruce A,Donoho D,Gao Hongye. Wavlete analysis[C]// IEEE Spectrum,1996: 26-35.
[9]Grossmann A,Morlet J. Decomposition of Hardy Functions into Square Integrable Wavelets of Constant Shape[J]. SIAM Journal on Mathematical Analysis,1984,15(4): 14.
[10]王济. MATLAB在振动信号处理中的应用[M].北京: 中国水利水电出版社,2006: 134-135.
(责任编辑: 陈曦)
An Accurate Computation Method of Vibration Level Based on Comb Band-stop Filter
SUN Tao,GAO Hui-zhong
(The 705 Research Institute,China Shipbuilding Industry Corporation,Xi′an 710075,China)
The existing 1/3 octave spectrum approaches are usually supposed to test signals without interference. Obviously,this strategy is no more effective when confronted with the signals containing band noise. In this paper,aiming at the regular noise interference,such as comb noise,the Fourier kernel function is employed to construct a comb bandstop filter,and further the filter is combined with the 1/3 octave spectrum to remove the effects exerted by noise. The proposed strategy can remove the interference in frequency domain and calculate the filtered vibration level more efficiently and conveniently,compared with the existing approaches. For the vibration signals with regular noise interference in the power test of a propulsion system,proper revision and consequent reevaluation can avoid repeated tests and save test costs.
propulsion system; vibration noise; signal process; 1/3 octave spectrum
TJ630.32; TB523
A
1673-1948(2015)02-0119-05
2014-11-18;
2015-01-08.
海军装备重大专项预研(40110),船舶预研支撑技术基金(14J4.4.1)
孙涛(1977-),男,博士,高级工程师,主要研究方向为测试测量技术、振源识别与故障诊断、多物理场耦合仿真、动力试验技术及其系统设计.
