火箭助飞鱼雷无伞段运动稳定性分析及仿真
2015-10-24王改娣石小龙刘孟秦
王改娣, 石小龙, 刘孟秦
(中国船舶重工集团公司 第705研究所, 陕西 西安, 710075)
火箭助飞鱼雷无伞段运动稳定性分析及仿真
王改娣,石小龙,刘孟秦
(中国船舶重工集团公司 第705研究所, 陕西 西安, 710075)
分析了影响火箭助飞鱼雷无伞段运动稳定性因素, 建立了干扰运动数学模型, 进行了不同干扰条件下的数学仿真。仿真结果表明, 火箭助飞鱼雷无伞段自由飞行运动具有非稳定、易发散特点, 这一结果可为火箭助飞鱼雷雷箭分离条件的确定和无伞段弹道设计和改进提供参考。
火箭助飞鱼雷; 无伞段运动; 干扰
0 引言
众所周知, 火箭助飞鱼雷(以下简称助飞鱼雷)从水面舰艇或潜艇发射后, 由运载体携带, 按照预定的助飞弹道和飞行路线进行空中飞行[1-2],到达预定的空中位置时, 运载体与战斗载荷分离(即雷箭分离), 此后进入空中雷伞运动阶段。雷伞运动弹道属于无控制无动力飞行弹道, 在雷箭弹道和水下弹道之间起着承上启下的作用, 在实际工程中, 主要通过对雷箭分离参数的约束、开伞动作时序的确定以及降落伞参数的设计来保证助飞鱼雷的雷箭安全分离和雷伞空中运动的减速和稳定, 并在一定的留空时间内满足鱼雷入水参数和落点精度的要求。
助飞鱼雷的无伞段是指从雷箭分离开始至降落伞打开的运动段, 鱼雷在该段完全处于自由飞行状态, 很容易受到外界干扰, 一旦无伞段运动发散, 雷体姿态就会发生很大变化, 不但影响鱼雷开伞过程和后续空中运动, 而且会严重影响雷箭分离的安全性, 甚至发生雷体与运载体残骸发生干涉或碰撞事故, 造成不可估量的损失[3-4]。
文章主要从理论上对助飞鱼雷雷箭分离后初期的无伞段运动稳定性进行分析和研究, 其目的是能够为助飞鱼雷战斗载荷气动特性改进方向及弹道设计提供理论帮助, 以增大无伞段运动稳定性, 提高雷箭分离安全性。
1 无伞段受力特点及稳定性分析
助飞鱼雷的战斗载荷由水下光雷体和空投附件组成, 在雷箭分离后, 其运动首先是无伞状态下的自由飞行, 直到空投附件中的降落伞打开。在降落伞打开之前的无伞段, 鱼雷主要受到重力和气动力作用, 其中, 气动力与战斗载荷的外形有关, 而装配有空投附件的战斗载荷外形不同于水下光雷体, 所以气动特性也不同于水下流体动力特性, 而是具有小阻尼、非线性和非定常的特点, 这些特点与无伞段稳定性相关。
助飞鱼雷无伞段稳定性[2,5]是指鱼雷在自由飞行过程中受到外界干扰(干扰力和干扰力矩)作用后, 能否恢复到原来运动状态的能力, 若能恢复到原飞行状态, 则鱼雷运动是稳定的, 若不能恢复到原来的飞行状态, 甚至偏差越来越大(运动参数发散), 则鱼雷运动是不稳定的。
稳定性包括静稳定性和动稳定性[6], 静稳定性仅说明鱼雷受到干扰后, 所产生的力矩是恢复力矩还是颠覆力矩即变化趋势, 它不能完全说明鱼雷运动稳定性。动稳定性指鱼雷在运动状态中的真实稳定性, 即鱼雷运动过程受到干扰后, 能否恢复到原来运动状态的能力。助飞鱼雷无伞段稳定性与战斗载荷的外形结构、气动布局以及衡重参数等密切相关。
由于助飞鱼雷在无伞段运动是无控自由的,在鱼雷设计特性确定后, 影响鱼雷运动稳定性的因素就取决于所受的各种干扰。如果按照作用时间长短来分, 干扰可分为经常作用干扰和瞬时作用干扰[3]。经常作用干扰如工艺误差、安装误差、舵面偏离零位等, 对于这种干扰, 动态分析时可作为一种常值干扰力和干扰力矩来处理。瞬时作用干扰如雷箭分离时起始扰动、高空瞬时阵风、开伞动作等, 这种干扰作用的结果往往使鱼雷运动参数出现较大偏差, 动态稳定性就是研究瞬时干扰对鱼雷运动的影响。
下面将主要对助飞鱼雷无伞段动态稳定性进行数学建模和仿真分析。
2 鱼雷稳定性数学模型
2.1干扰运动数学模型
假设助飞鱼雷在某一平衡点附近进行准定常水平直线运动, 利用小扰动假设理论, 可对其运动方程进行线性化处理, 以助飞雷纵向运动为例, 其线性化后的自由扰动运动用矩阵方程表达形式为
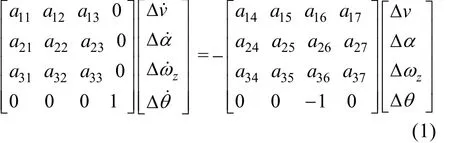
式中的变量Δv,Δα,Δωz和Δθ分别为受干扰后的速度偏量、攻角偏量、俯仰角速度偏量和俯仰角偏量, 系数矩阵aij(i=1~3,j=1~7)称为动力系数,表征了鱼雷的动力学特性, 它与鱼雷气动参数、衡重参数以及未扰动前运动参数等有关。
利用系数冻结法, 假设aij(i=1~3,j=1~7)为常值, 则式(1)就是常系数线性齐次微分方程组,只要给出初始干扰条件Δv0,Δα0,Δωz0和Δθ0, 就可求出鱼雷受干扰后的运动参数变化偏量。
通常, 研究雷体特性就是研究扰动速度为零时的鱼雷自由运动, 它反映了鱼雷固有运动特性,所以, 忽略式(1)中第1个方程, 并令Δv=0, 得到描述雷体特性方程的矩阵表达形式
21世纪以来,国家逐渐加强了生态环境工程投入与经济制裁。2007年的国家环境保护“十一五”规划中规定,全国环保投资约占同期国内生产总值的1.35℅,可征收排污费750亿元。到了2011年的国家环境保护“十二五”规划,光八项重项工程,就拟投资1.5万亿元。在各类先进人物的推举中,也出现了环保英雄孟祥民这样的新型领域典型。民众对环境保护的关注与日俱增,从限塑令的施行到电动车锂离子电池的使用,再到因活熊取胆抵制归真堂上市的举措,可见出在当代社会民众中发挥生态美学的空间与力度越来越大。

式(1)和式(2)即为描述助飞鱼雷干扰运动的数学模型。
2.2稳定性判别准则
为了研究助飞鱼雷在无伞段受到干扰后运动是否稳定, 需要分析自由扰动运动的性质, 为此,对式(2)进行变换处理, 得到如下特征根方程

式(3)中D3~D0是特征方程系数, 由动力系数表达如下
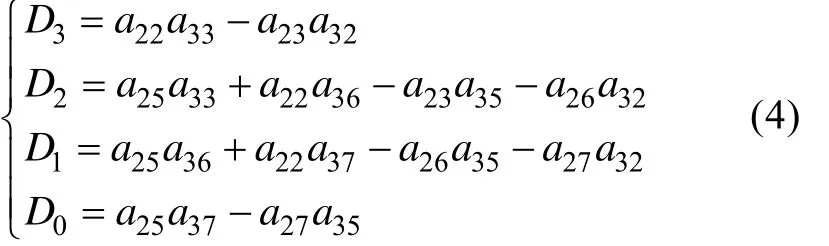
可以看出, 特征方程有3个根S3~S1, 这3个根可能是实数, 也可能是共轭复数, 因此自由扰动运动可能有下列2种情况。
1) 3个根均为实数
此种情况下的自由扰动运动由3个非周期运动组成, 3个根中只要有1个正根, 则所有偏量Δα,Δωz和Δθ均随时间增长而无限增大, 即自由扰动运动发散。
2) 1个根为实数, 2个根为共轭复数
此种情况下的自由扰动运动由1个非周期运动和1个振荡运动叠加组成, 在实根和复根实部中, 只要有1个符号为正, 则所有偏量Δα,Δωz和Δθ均随时间增长而无限增大, 即自由扰动运动发散。
综上所述, 助飞鱼雷无伞段运动的稳定性可由特征方程(3)的根来说明, 即如果所有实根或复根的实部都是负的, 则鱼雷运动是稳定的, 只要有1个实根或1对复根的实部为正, 则鱼雷运动是不稳定的, 在所有实根或复根的实部中, 只要有1个等于0, 而其余均为负, 则鱼雷运动是中立稳定的。
3 特征根计算和干扰仿真
在已知衡重参数、气动参数和雷箭分离参数等条件下, 通过计算特征根和对干扰影响仿真来对助飞鱼雷无伞段运动稳定性进行具体分析。
3.1特征根计算
表1给出了助飞鱼雷不同雷箭分离速度V0和分离攻角α0下准定常运动时的特征根计算结果。

表1 不同分离参数下特征根Table 1 Characteristic root for different separation parameters
从表1计算结果可以看出:
1) 无论初始分离条件如何, 特征根均为3个不同实根, 说明该助飞鱼雷无伞段自由运动由3个非周期运动组成, 但由于存在2个正根S1和S3, 该自由运动又是发散的;
2) 同一分离速度V0下, 正根S3随分离攻角α0增大而增大, 说明分离攻角越大发散程度越大;
3) 同一分离攻角α0下, 正根S1随分离速度V0增大而增大, 说明分离速度越大发散程度越大。
综上所述, 助飞鱼雷无伞段自由运动是不稳定的, 其不稳定程度与雷箭分离速度和分离攻角有关。
3.2干扰影响仿真
假设雷箭分离时的速度V0=100 m/s, 攻角为α0=1°, 在此条件下助飞鱼雷进行准定常运动, 在运动过程中受到某种干扰后, 速度和攻角分别发生了变化, 并将此变化作为初始条件, 利用文中建立的干扰运动数学模型进行鱼雷无伞段自由运动仿真计算。
1) 速度干扰 设初始速度干扰分别为Δ V0=5 m/s, 10 m/s, 15 m/s, 其他干扰为0, 则鱼雷运动参数中的速度v、攻角α、俯仰角速度ωz和俯仰角θ变化的仿真结果见图1。从图1可以看出, 初始速度干扰Δ V0越大, 其运动参数发散越快, 其变化趋势是鱼雷攻角增大、俯仰角速度增大及俯仰角增大。
2) 攻角干扰 设初始攻角干扰分别为Δ α0=1°, 5°, 10°, 其他干扰为0, 则鱼雷运动参数中的速度、攻角、俯仰角速度和俯仰角变化的仿真结果见图2。从图2可以看出, 初始攻角干扰Δ α0对鱼雷运动参数影响结果同初始速度干扰, 同样使运动参数发散, 其发散趋势是随干扰Δα0增大而增大。
仿真结果表明, 在干扰影响下, 助飞鱼雷无伞段自由运动是发散的, 这与3.1节特征根计算结果相符。
4 结束语
文章针对火箭助飞鱼雷在雷箭分离后无伞段自由飞运动稳定性进行了研究, 首先分析了影响助飞鱼雷稳定性的主要因素, 建立了干扰运动数学模型, 给出了稳定性判别准则, 然后通过设置不同的干扰条件, 对鱼雷受干扰后的运动进行了数学仿真。结果表明, 助飞雷无伞段运动是不稳定的, 其不稳定程度与所受干扰有关, 干扰越大,越容易发散, 该研究结果可为火箭助飞鱼雷雷箭分离安全性设计和无伞段气动特性改进及弹道设计方向提供帮助。
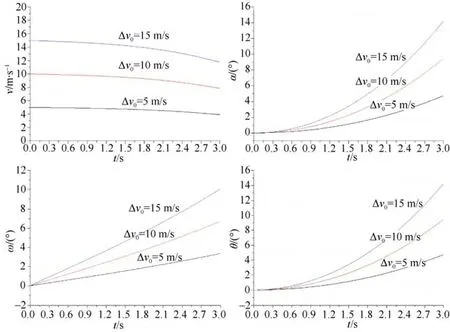
图1 速度干扰下的运动参数变化Fig. 1 Variation of motion parameters with interference of speed

图2 攻角干扰下的运动参数变化Fig. 2 Variation of motion parameters with interference of attack angle
[1] 赵育善, 吴斌. 导弹引论[M]. 西安: 西北工业大学出版社, 2002.
[2] 钱杏芳, 林瑞雄, 赵亚男. 导弹飞行动力学[M]. 北京:北京理工大学出版社, 2008.
[3] 崔洪坤, 孙振新. 飞航式火箭助飞鱼雷弹道建模与仿真[J]. 指挥控制与仿真, 2012, 34(2): 75-79.
Cui Hong-kun, Sun Zhen-xin. Ballistic Modeling and Simulation of Cruising Rocket-Assisted Torpedo[J]. Command Control & Simulation, 2012, 34(2): 75-79.
[4] 吝龙艳. 火箭助飞鱼雷雷体动力学特性分析[J]. 鱼雷技术, 2004, 12(3): 21-24.
[5] 何植岱, 高浩. 高等飞行动力学[M]. 西安: 西北工业大学出版社, 1990.
[6] 詹致详, 陈景熙. 鱼雷航行力学[M]. 西安: 西北工业大学出版社, 2005.
(责任编辑: 陈曦)
Analysis and Simulation of Moving Stability for Rocket-assisted Torpedo without Umbrella
WANG Gai-di,SHI Xiao-long,LIU Meng-qin
(The 705 Research Institute, China Shipbuilding Industry Corporation, Xi′an 710075, China)
This paper analyzes the factors influencing moving stability of a rocket-assisted torpedo without umbrella,builds a mathematical model of movement with interference, and performs simulation with different interference. Simulation result shows that the free flight movement of the rocket-assisted torpedo without umbrella has the unstable and divergent characteristics. This result may provide a reference for determining separation condition of a rocket and a torpedo, and for trajectory design and improvement of a rocket-assisted torpedo without umbrella.
rocket-assisted torpedo; movement of rocket-assisted torpedo without umbrella; interference
TJ630.1
A
1673-1948(2015)06-0401-04
10.11993/j.issn.1673-1948.2015.06.001
2015-08-14,
2015-10-19.
王改娣(1964-), 女, 研究员, 主要从事鱼雷总体性能和弹道仿真建模研究工作.
