太阳能无人机螺旋桨滑流气动特性分析
2015-10-22王红波祝小平周洲许晓平
王红波,祝小平,周洲,许晓平
1.西北工业大学航空学院,陕西西安 710072 2.西北工业大学无人机特种技术重点实验室,陕西西安 710065
太阳能无人机螺旋桨滑流气动特性分析
王红波1,2,祝小平2,周洲1,2,许晓平1,2
1.西北工业大学航空学院,陕西西安 710072 2.西北工业大学无人机特种技术重点实验室,陕西西安 710065
针对螺旋桨滑流对太阳能无人机气动性能的影响,基于结构/非结构混合网格,首先使用多重参考系方法对螺旋桨滑流进行准定常计算以获得初始流场,再使用滑移网格方法对螺旋桨的真实转动进行非定常数值模拟。采用NASA涵道螺旋桨进行算例验证,其计算结果与实验值误差仅为5.3%,证明了计算方法的可靠性和准确性,在此基础上数值模拟了滑流在不同转速和来流迎角下对全机气动力的影响。结果表明:螺旋桨滑流具有增升增阻的效果,且转速越高影响越显著,升力、阻力增量最大值分别达到了26.7%和34.7%,全机升阻比则明显减小,最大减小量为26.26%。滑流对机翼弦向压力分布的影响主要集中在前缘,并且在螺旋桨中心轴两侧分别出现了压力最大和最小值;而越接近机翼后缘时,滑流对压力分布的影响越小。
太阳能无人机;螺旋桨;滑流;非定常;多重参考系;滑移网格
作为新能源飞行器的典型代表,太阳能飞机以清洁太阳能为持续能量来源从而实现零油耗、超高空、不间断飞行。国内外学者针对长航时的飞行目标都进行了大量研究,但其研究重心主要是从能量角度着手[1],即提高太阳能电池效率、储能电池比能量等措施实现长航时飞行。而从气动布局方面着手提高航时问题给予的关注极少。
对于螺旋桨飞机而言,螺旋桨滑流对全机气动特性的影响一直是空气动力学研究的难点,其原因在于螺旋桨滑流高速旋转并与机翼绕流相互干扰,产生了复杂的非定常效应。而太阳能飞机又不同于常规螺旋桨飞机,它多采用分布式螺旋桨推进系统,当多个螺旋桨同时旋转时,机翼绝大部分面积都处在滑流影响中,全机与螺旋桨的气动干扰将会更加明显,从而给太阳能飞机气动性能分析和气动布局设计带来了较大困难。
对于螺旋桨滑流的气动计算,早期的动量理论、叶素理论、涡流理论[2]已经不适用于螺旋桨与机翼之间复杂的气动干扰问题。随着计算流体力学(CFD)技术的发展,CFD的计算精度和可信度有了很大提高,将其用于滑流的数值模拟逐渐成为一种有效的计算方法。基于动量理论的激励盘模型[3-4]由于方法简单、计算量小的优点得到广泛使用,但它的缺点在于没有考虑螺旋桨的旋转运动以及桨叶的几何参数与螺旋桨拉力的关系,无法得到流场细节。对于较高精度的螺旋桨滑流计算,多重参考系(multiple reference frames,MRF)计算方法[5]将非定常问题转化为定常问题,降低了求解难度且计算效率较高,然而机翼对螺旋桨存在气动干扰时,此方法的计算精度有所降低;而对于更高精度的非定常数值模拟,国内外都做了大量研究[6-8],非定常计算更接近螺旋桨的真实流动,但是对计算条件要求较高,计算周期较长,尤其是对全机装载多个螺旋桨的太阳能飞机而言,如何提高计算效率成为研究该类型飞机滑流特性最突出的难点。
目前使用CFD方法对螺旋桨滑流的数值模拟主要集中于计算方法的验证以及流场特性的分析,且在计算螺旋桨与机翼的气动干扰时,桨的个数相对较少。对于完全使用CFD方法用于太阳能飞机螺旋桨滑流特性的数值计算并对螺旋桨滑流干扰下的全机整体气动性能进行分析,国内外公开发表文献[9]十分稀少。
为了提高CFD计算效率和计算精度,本文将兼顾定常与非定常计算各自的优点,将2种方法结合使用:先以MRF方法进行定常计算作为非定常的初始流场从而缩短计算时间,在此基础上再采用滑移网格方法[10-12]非定常模拟螺旋桨的旋转运动以提高计算精度。求解过程中以雷诺平均Navier-Stokes (N-S)方程为控制方程首先对NASA实验涵道螺旋桨模型进行CFD方法验证,再对太阳能飞机在不同螺旋桨转速下的气动性能进行气动计算,并分析多个螺旋桨滑流对全机的影响规律。
1 数值求解方法
1.1控制方程
文中所采用的控制方程为非定常三维可压缩N-S方程,在直角坐标系下守恒形式的N-S方程表达如下[13]

式中,Q为守恒变量项,Fc为无黏通量,Fv是黏性通量,n表示边界外法线方向,Ω为控制体,∂Ω表示控制体单元边界。空间离散采用Roe格式,黏性通量采用二阶中心差分离散。
1.2双时间推进
对于非定常流动计算,采用基于隐式的LU-SGS (lower-upper symmetric Gauss-Seidel)双时间步法对控制方程进行物理时间的推进,其表达式如下[14]
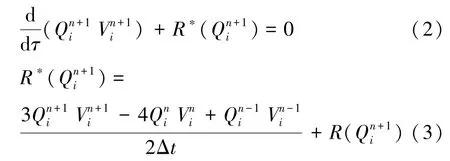
2 算例验证模型及结果
为验证文中CFD计算方法的可信度,选取有详细风洞实验数据和几何模型数据的涵道螺旋桨模型[15]进行算例验证。涵道螺旋桨为三桨叶构型,桨叶直径0.381 m,桨叶剖面翼型为NACA6412,桨叶转速8 000 r/min。具体几何参数见文献[15]。
为减小计算误差,根据文献中的几何数据建立模型时,充分考虑了螺旋桨桨叶叶素安装角、叶素弦长、桨叶与内涵道间隙大小、桨叶与轮毂连接方式等具体几何参数。对于螺旋桨这样旋转机械的网格生成,需要将整个流场划分为2个计算域:包围螺旋桨的圆柱形封闭空间为旋转运动区域,对旋转区域划分非结构网格[16]能够降低螺旋桨桨叶的网格生成难度,提高网格生成效率。在桨尖与涵道内壁的间隙内,网格进行了适当加密;圆柱形外部及远场之间的区域为静止区域,在此区域划分结构网格从而节约计算时间,涵道螺旋桨表面网格如图1所示。

图1 涵道螺旋桨网格
总的网格量由结构和非结构网格构成了530万的混合网格,先采用MRF方法获得定常流场后再使用滑移网格求解技术对涵道螺旋桨的旋转进行非定常数值模拟,湍流模型选择剪应力输运(shear stress transport,SST)两方程模型。这种模型对于高速旋转的机械部件能够保持较高的计算精度[11]。计算时大气条件为标准海平面,自由来流速度30.48 m/ s,雷诺数基于涵道弦长的量值为Re=5.5×105,以上计算参数均为实验条件。
表1给出了0°迎角下涵道螺旋桨桨叶拉力时均计算结果与实验值[15]的对比,其计算误差只有5.3%,证明了基于结构/非结构的混合网格生成方法以及采用滑移网格求解技术对带有旋转部件的气动力的计算具有较高的精度。
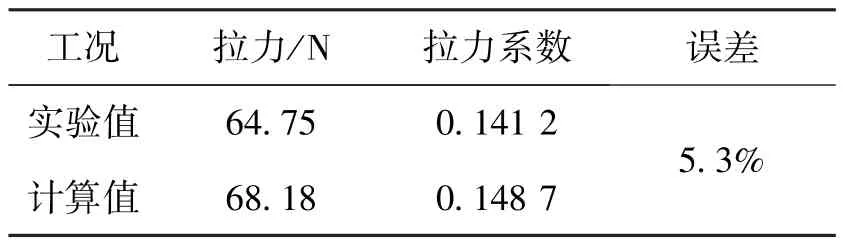
表1 涵道螺旋桨结果对比
3 太阳能飞机螺旋桨/机翼干扰下气动力计算分析
文中所计算的太阳能无人机全机采用鸭翼+主机翼的气动布局,如图2所示。全机巡航高度25 km,基于机翼弦长的雷诺数为Re=3.8×105,马赫数Ma=0.177,螺旋桨为两叶桨,桨叶半径1.05 m,分别计算螺旋桨转速为1 000 r/min、1 400 r/min、1 800 r/min以及来流迎角在-6°~12°范围内全机的气动力。由于螺旋桨滑流与机翼的相互干扰会产生复杂的非定常效应,计算中最好采用全模计算,然而考虑到1号螺旋桨(如图2a)所示)到全机对称面的距离为螺旋桨直径的2倍,两者相距较远,其产生的滑流对大展弦比太阳能飞机的气动力影响较弱,因此采用半模计算不会带来较大的计算误差,同时可以显著节约计算时间,全机半模表面网格如图2b)所示。气流方向沿X坐标轴正向,6个螺旋桨的旋转方向顺着自由来流方向逆时针旋转,Y方向为展长方向。

图2 太阳能无人机半模气动布局
计算网格的生成采用算例验证过程中的方法,每个螺旋桨包围的圆柱型旋转区域划分80万非结构网格,6个螺旋桨共480万,在剩余区域即静止区域划分450万结构网格。
文中的计算方法仍与算例验证的相同。在非定常计算中,桨叶旋转1周被分为180个时间步,因此3个不同的转速对应的目标时间步长分别为3.8× 10-4s、2.38×10-4s、1.85×10-4s。在非定常计算初始阶段,先设定较大的时间步长以缩短起始阶段的不稳定过程,当结果出现周期性振荡时再减小时间步从而提高计算精度,但每次时间步的减小量最好不超过上次时间步的20%。在最后几个旋转周期内,时间步减小到目标时间步后便不再改变。在8 个CPU,32G内存计算机上,每个迎角定常计算平均耗时3天,非定常计算平均耗时18天,共计30个计算状态。需要说明的是,文中所有的计算结果都是对桨叶旋转一圈的时间平均。
此外,本文对非定常的计算效率做了对比,结果发现:如果在整个非定常计算过程中时间步直接设定为目标时间步长且保持不变,虽然计算结果十分接近于文中所采用的方法的结果,然则非定常计算耗时增加到了26天。由此证明,文中所采用的计算方法在保证计算结果精度的同时能够明显节约计算时间,具有较高的计算效率。
3.1气动力对比
图3是不同螺旋桨转速下时均升力系数对比。图中,propeller off代表无螺旋桨的干净构型布局。

图3 不同转速下的升力系数曲线
可以发现:螺旋桨滑流对全机具有一定的增升作用。在正迎角范围内,随迎角的增大,全机升力系数增量ΔCL逐渐增大;而在相同来流迎角下,螺旋桨转速越高,滑流增升作用越明显,升力系数的增量在迎角12°以及转速1 800 r/min时其量值可达26.7%。而在负迎角范围内(-6°~-2°),不同转速下的升力系数都十分接近于干净构型升力,表明此时螺旋桨滑流与转速的变化引起的增升作用十分有限,可以忽略不计。
虽然螺旋桨旋转引起了复杂的非定常效应,但升力随迎角的变化规律并未受到影响,小迎角范围内,两者仍保持线性关系。螺旋桨滑流显著提高了最大升力系数,使升力线斜率也有所增加,这一结果与文献[17]的实验结论比较一致。
图4为不同转速下阻力系数随迎角的变化关系,其变化规律类似于图3升力系数变化情况:在负迎角下,桨叶转速变化对阻力系数几乎没有影响;而迎角为正时,随迎角的增大,螺旋桨滑流使全机阻力迅速增长,并且转速越高,阻力增加越快。在12°迎角和1 800 r/min转速条件下,相对于干净构型布局,阻力系数增量为34.7%,是相同来流条件下升力系数增量的1.3倍。由此可见,螺旋桨滑流在增加升力的同时也带来了较大的阻力,产生“增升增阻”的效果,且阻力的增加比升力更迅速。

图4 不同转速下阻力系数曲线
为进一步分析阻力随迎角的变化情况,表2给出了螺旋桨转速1 400 r/min时不同迎角下压差阻力、摩擦阻力、总阻力系数的对比。

表2 不同迎角下阻力系数对比
总阻力系数的增大应归因于压差阻力的迅速提高,其在总阻力中的比例由-4°迎角时的60%迅速提高到了10°迎角时的96%。
螺旋桨滑流引起全机“增升增阻”的结果必然影响到升阻比的变化。图5给出了不同转速下全机升阻比随迎角的变化关系。
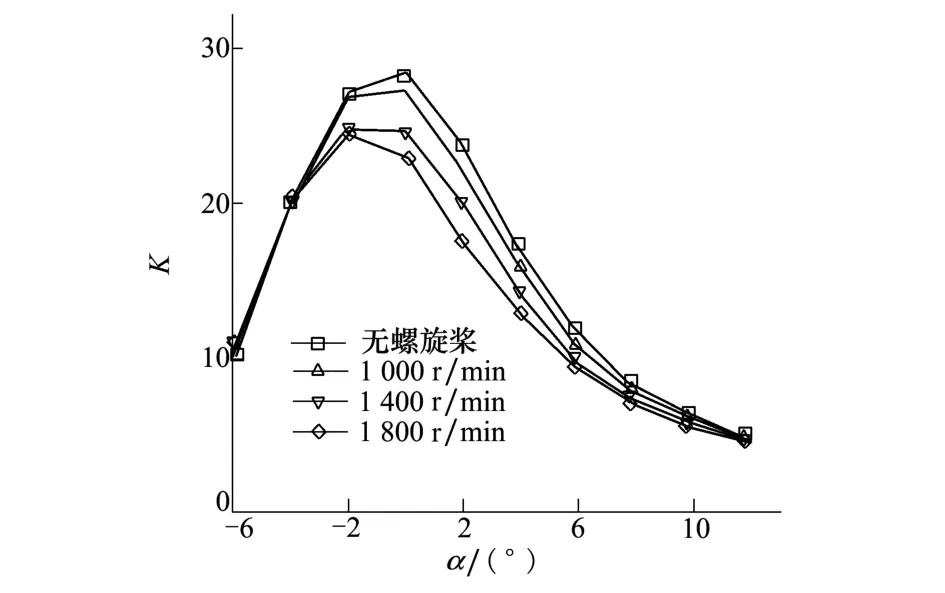
图5 不同转速下升阻比曲线
计算结果表明,在负迎角下,不同转速下的升阻比都十分接近,说明此时滑流的影响微弱到可以忽略不计;随迎角的逐渐增大,滑流作用使升阻比反而减小,且转速越高,升阻比减小越多;升阻比的最大减小量在迎角2°以及转速1 800 r/min时减小了26.26%,当迎角进一步增大时,升力和阻力都迅速增大,所获得的增升效果被阻力的增量所抵消,从而使不同转速下的升阻比又逐渐接近于干净构型布局的情况。
3.2压力分布对比

图6 螺旋桨滑流对弦向压力分布的影响
图6为螺旋桨转速1 400 r/min,来流迎角-6° 和0°时螺旋桨滑流对机翼不同展向位置的时均弦向压力分布的影响,展向位置在图2a)中已经标示出。需要说明的是:对于全机干净构型,即无螺旋桨情况(no propeller),计算结果表明,由于展向位置y/b=30%和y/b=33%两者十分接近,它们的弦向压力分布相差很小,几乎完全吻合,因此在图6a)和图6b)中,干净构型(no propeller)的弦向压力分布只给出了展向位置y/b=30%的计算结果。
螺旋桨的旋转会在它转轴的两侧同时诱导出上洗和下洗效应。在本文中,由于螺旋桨沿X轴正向逆时针旋转,因此y/b=30%和y/b=33%2个展向位置分别处在上洗和下洗区域内。对处在下洗作用内的翼段,机翼实际来流迎角小于自由来流迎角,而处在上洗作用内的机翼,其实际迎角大于来流迎角。
从图6a)中可以看到在负来流迎角下,干净构型布局(no propeller)的机翼前缘出现了负升力。当有滑流影响时,在y/b=33%位置处,滑流诱导的下洗作用进一步使机翼前缘的负升力绝对值增大,降低了该翼段范围的升力;而在y/b=30%位置处,受上洗作用影响,整个弦长范围都保持为正升力,
然而上洗作用获得的升力增益几乎被下洗作用诱导的负升力所抵消,机翼总升力变化不大,这一结果在图3中的体现为:负来流迎角下,不同转速时的升力系数与干净构型布局的情况十分接近。
来流迎角增大时,如图6b)所示,y/b=30%和y/b=33%处上翼面的负压和下翼面的正压的绝对值都同时增大,同时y/b=33%处机翼前缘的负升力又显著减小,两者的共同作用使机翼的总升力随迎角的增大迅速提高,螺旋桨滑流的增升作用愈加明显。这一现象即为图3中升力系数随来流迎角和转速提高而迅速增大的原因。
当弦向位置接近机翼后缘时,其压力分布逐渐接近于干净构型的情况,这说明螺旋桨滑流诱导的上洗和下洗作用主要对机翼前缘的压力分布产生显著影响,弦向位置越接近后缘则滑流影响越小。
图7是螺旋桨在1 400 r/min转速时0°迎角下机翼1/4弦长位置处展向压力分布与干净构型的对比。图中,y/b=0代表机翼翼尖位置,y/b=1为全机对称面位置。

图7 1/4弦线展向时均压力分布
显然,全机半模6个拉力螺旋桨产生的滑流使机翼展向压力分布出现了6个显著的“波峰”和“波谷”。螺旋桨转轴两侧的压力分布呈现出明显的反对称性。这一现象出现的原因正如图6所反映出的结论,即螺旋桨滑流的影响主要体现在显著改变机翼前缘压力分布,转轴左侧波峰的出现是由于滑流诱导的上洗作用引起机翼前缘压差显著增大,而下洗作用导致机翼前缘压差明显减小,于是在转轴右侧出现波谷。由于波峰值大于波谷值,机翼总的升力有所增加,间接体现了滑流的增升效果。
本文的太阳能无人机模型采用的是分布式拉力螺旋桨且等间距布置,展向压力分布表明机翼绕流几乎完全处于螺旋桨滑流影响中,并且滑流的影响也体现出了三维效应,即靠近翼尖位置,波峰值较小,此处机翼升力也最小;当逐渐接近机身对称面时则波峰值与升力都渐渐增大。
3.3流场分布
图8和图9分别是转速1 400 r/min、12°迎角下不同展向位置处时均弦向流线与干净构型的对比。
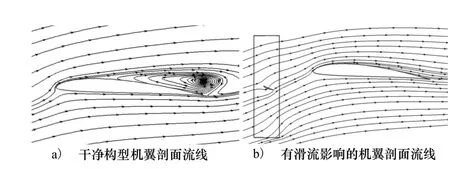
图8 y/b=30%展向位置处不同气动构型机翼剖面流线
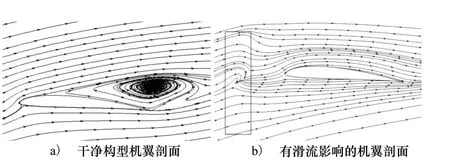
图9 y/b=33%展向位置处不同气动构型机翼剖面流线
在12°迎角下,干净构型机翼后缘已经发生较大范围的分离流动,而处在滑流中的机翼绕流则仍然保持附着流动,这是由于螺旋桨的旋转对自由来流有明显的加速效应,提高了气流的动能,从而有效延迟滑流区内气流的分离,这一结果与文献[18-19]的实验结论相一致。从升力系数曲线(图3)中可知,干净构型布局在8°迎角开始失速,而滑流的影响使全机的失速迎角提高到10°。
另外对比图8b)和图9b)可知:自由来流经过螺旋桨之后,受到上洗作用影响(见图8b))时,流线向上偏折,而下洗影响(见图9b))使流线则明显下偏。因此对于同样的来流迎角,滑流区内不同的翼段具有不同的来流情况,升阻力具有较大的差异。以螺旋桨转轴为分界线,其两侧对称位置上的流场特征和气动力整体上呈现反对称分布。

图10 不同气动构型的机翼上表面压力分布云图

图11 不同气动构型的机翼下表面压力分布云图
图10和图11分别给出了螺旋桨转速1 400 r/ min以及0°迎角下,4号螺旋桨周围机翼上、下表面的压力云图与干净构型的对比,图中标示出的压力值都是在机翼相同坐标点上的计算结果,图中虚线的间距代表了螺旋桨直径范围。
从压力等值线的分布趋势可以看出,大展弦比布局的干净构型机翼的压力分布沿展向变化较为缓慢,而螺旋桨滑流的加速效应明显改变了这一特征。由于机翼前缘对滑流存在阻塞效应,再加上滑流加速效应以及滑流改变转轴两侧有效迎角的现象,这三者共同作用导致机翼前缘压力变化不论是在弦向还是展向方向变化都比较剧烈,所以,不论上下翼面,其等值线在机翼前缘的分布最为密集。在螺旋桨转轴左侧,上翼面前缘存在明显的低压区而下翼面前缘具有明显的高压区;在转轴的右侧,情况则刚好相反,即高压区在上,低压区在下。这一结果正好对应着图7中所表现出的压力波峰和波谷现象。而波峰和波谷的位置取决于螺旋桨的旋转方向。
4 结 论
本文通过对太阳能无人机分布式螺旋桨滑流影响下的全机气动性能的数值模拟,得出以下结论:
1)随迎角的增大,螺旋桨滑流能够显著提高全机升力但同时也增加了阻力,产生“增升增阻”的效果,且阻力的增量大于升力增量导致全机升阻比减小,螺旋桨转速提高时,增升增阻的现象更为明显,升阻比下降更多。
2)螺旋桨旋转对机翼扰流具有明显的加速效应,滑流对机翼弦向压力分布的影响主要集中在机翼前缘,前缘压力分布在转轴两侧出现了明显的波峰和波谷现象,当逐渐靠近机翼后缘时,压力分布则接近干净构型机翼的分布情况,滑流影响有所减弱。
3)螺旋桨滑流在转轴两侧同时产生了上洗和下洗效应,相应的机翼实际迎角分别大于和小于自由来流迎角;此外,在大迎角下,螺旋桨滑流能推迟滑流区内机翼绕流的分离流动,提高全机的失速迎角。
综上所述,分布式螺旋桨滑流对太阳能无人机的气动性能的影响比较显著,尤其是“增升增阻”导致升阻比减小的现象对太阳能飞机的长航时飞行则是十分不利的因素,削弱了大展弦比布局的气动优势,因此进一步开展分布式螺旋桨滑流影响下增升减阻的研究对于太阳能飞机而言则十分有必要。
[1] 昌敏.广纬度域驻留太阳能飞机设计及其动力学特性研究[D].西安:西北工业大学,2013
Chang Min.Research on Design Methodology and Flight Dynamics of Solar-Powered Stratospheric Aircraft from Low to Middle Latitudes[D].Xi′an:Northwestern Polytechnical University,2013(in Chinese)
[2] 刘沛清.空气螺旋桨理论及应用[M].北京:北京航空航天大学出版社,2006
Liu Peiqing.Air Propeller Theory and Its Application[M].Beijing,Beihang University Press,2006(in Chinese)
[3] Zori L A J,Rajagopalan R G.Navier-Stokes Calculations of Rotor-Airframe Interaction in Forward Flight[J].Journal of the A-merican Helicopter Society,1995,40(2):57-67
[4] 段中喆,刘沛清,屈秋林,等.修正的动力盘模型与三维模拟螺旋桨滑流比较[J].北京航空航天大学学报,2013,39 (5):585-589
Duan Zhongzhe,Liu Peiqing,Qu Qiulin,et al.Slipstream Characters Comparison of Improved Actuator Disk Model and 3D Propeller Numerical Simulation[J].Journal of Beijing University of Aeronautics and Astronautics,2013,39(5):585-589(in Chinese)
[5] 张刘,刘李涛,章荣平,等.螺旋桨粘性流场非定常数值模拟[J].航空动力学报,2013,28(12):2648-2654
Zhang Liu,Liu Litao,Zhang Rongping,et al.Unsteady Numerical Simulation of the Viscous Flow Fields of the Propeller[J]. Journal of Aerospace Power,2013,28(12):2648-2654(in Chinese)
[6] Stuermer A.Unsteady CFD Simulations of Propeller Installation Effects[R].AIAA-2006-4969
[7] 夏贞锋,杨永.螺旋桨滑流与机翼气动干扰的非定常数值模拟[J].航空学报,2011,32(7):1195-1201
Xia Zhenfeng,Yang Yong.Unsteady Numerical Simulation of Interaction Effects of Propeller and Wing[J].Acta Aeronautica et Astronautica Sinica,2011,32(7):1195-1201(in Chinese)
[8] 杨小川,王运涛,王光学,等.螺旋桨非定常滑流的高效数值模拟研究[J].空气动力学学报,2014,32(3):289-294
Yang Xiaochuan,Wang Yuntao,Wang Guangxue,et al.Numerical Simulation of Unsteady Propeller Slipstream[J].Acta Aerodynamic Sinica,2014,32(3):289-294(in Chinese)
[9] Fu Weijia,Li Jie,Wang Haojie.Numerical Simulation of Propeller Slipstream Effect on A Propeller-Driven Unmanned Aerical Vehicle[C]∥Procedia Engineering,International Conference on Advances in Computational Modeling and Simulation. Kunming,China,2012:150-155
[10]Liu Tsunglung.Application of the Sliding Mesh Technique for Helicopter Rotor Flow Simulation[J].Journal of Aeronautics,Astronautics and Aviation,2012,44(3):201-210
[11]Thouault N,Breitsamter C,Adams N A.Numerical and Experimental Analysis of a Generic Fan-in-Wing Configuration[J].Journal of Aircraft,2009,46(2):656-666
[12]许和勇.基于动态嵌套网格的非定常流动数值模拟[D].西安:西北工业大学,2009
Xu Heyong.Numerical Simulations of Unsteady Flow Fields Based on Dynamic Overset Grids[D].Xi′an,Northwestern Ploytechnical University,2009(in Chinese)
[13]李鑫,白俊强,王昆.增升装置及机翼积冰数值模拟[J].航空动力学报,2013,28(12):2663-2670
Li Xin,Bai Junqiang,Wang Kun.Numerical Simulation of Ice Accretions on High-Lift System and Aircraft Wing[J].Journal of Aerospace Power,2013,28(12):2663-2670(in Chinese)
[14]范锐军.混合动力垂直起降飞翼气动布局及特性研究[D].西安:西北工业大学,2010
Fan Ruijun.Numerical Study on Aerodynamic Configuration and Characeristics of Hybrid-Powered VTOL Flying Wing UAV[D]. Xi′an,Northwestern Polytechnical University,2010(in Chinese)
[15]Grunwald K J,Goodson K W.Aerodynamic Loads on an Isolated Shrouded-Propeller Configuration for Angle of Attack from-10° to 110°[R].NASA TN D-995,1962
[16]叶靓,招启军,徐国华.基于非结构嵌套网格方法的旋翼地面效应数值模拟[J].航空学报,2009,30(5):780-786
Ye Liang,Zhao Qijun,Xu GuoHua.Numerical Simulation on Flowfield of Rotor in Ground Effect Based on Unstructured Embedded Grid Method[J].Acta Aeronautic et Aeronautic Sinica,2009,30(5):780-786(in Chinese)
[17]Makino F,Nagai H.Propeller Slipstream Interface with Wing Aerodynamic Characteristics of Mars Airplane at Low Reynolds Number[R].AIAA-2014-0744
[18]Ananda G K,Deters R W,Selig M S.Propeller Lnduced Flow Effects on Wings at Low Reynold Numbers[R].AIAA-2013-3193
[19]Sudhakar S,Kumar C,Aprivoli D,et al.Experimental Studies of Propeller Induced Flow Over a Typical Micro Air Vehicle[R]. AIAA-2013-0060
Aerodynamic Investigation on Propeller Slipstream Flows for Solar Powered Airplanes
Wang Hongbo1,2,Zhu Xiaoping2,Zhou Zhou1,2,Xu Xiaoping1,2
1.College of Aeronautics,Northwestern Polytechnical University,Xi′an 710072,China 2.Science and Technology on UAV Laboratory,Northewestern Ploytechnical University,Xi′an 710065,China
The aerodynamic characteristic on solar powered aircraft affected by propeller slipstream flows was investigated based on the structured/unstructured hybrid grid method.The effect of Propeller slipstreams was simulated with Multiple Reference Frames quasi steady method firstly in order to provide an initial flow field for the unsteady numerical simulation using sliding mesh methods.An experimental ducted propeller model belonging to NASA was used to verify the present methods and numerical results with a 5.3%error indicate a high level of agreement with experimental data;this demonstrates that the above methods have good accuracy to numerically simulate the aerodynamics of the solar powered aircraft at different propeller rotational speeds and angles of attack.According to the results,propeller slipstreams lead to notable lift and drag increments:the maximum lift increment and drag increment are respectively 26.7%and 34.7%.However,lift-to-drag ratio values for solar powered airplanes are reduced and the maximum decrement is 26.26%.The position where propeller slipstreams affect the chordwise pressure distribution mainly locates at the leading edge of the wing;this induces opposite pressure changes at the two sides of the propeller rotation shaft.However,the effect of the propeller slipstreams on the chordwise pressure distribution become little at the trailing edge of the wing.
aerodynamics,aircraft,angle of attack,computer simulation,drag coefficient,errors,experiments,flow fields,lift drag ratio,mathematical models,mesh generation,Navier Stokes equations,propellers,solar energy,multiple reference frames,sliding mesh,slipstream,solar powered aircraft,unsteady
V211
A
1000-2758(2015)06-0913-08
2015-03-17
国家“863”课题(2014AA7052002)资助
王红波(1986—),西北工业大学博士研究生,主要从事垂直起降无人机总体气动设计研究。
周洲(1966—),西北工业大学教授、博士生导师,主要从事无人机设计研究。zhouzhou@nwpu.edu.cn。
