浅述初中学生数学阅读能力的培养

杨汉勤

摘 要：阅读是人获取知识的主要手段之一。数学学习活动离不开数学阅读，学生学习活动离不开自主探究。数学阅读不仅是学生自主探究的过程，也是数学式思考、学习的过程。要让学生真正成为数学学习活动的主人，在从事多种数学学习活动、自主探索过程中，数学阅读是不可或缺的一种学习活动。从培养学生的数学阅读能力，使数学阅读真正成为数学学习活动说起，对近年来的教学实践进行了归纳和总结，和同行们一起探讨。

关键词：数学阅读;统计图表;学习活动

一、初中数学阅读教学环节薄弱的原因

从笔者对本校乃至周边学校的公开课、优质课等数学教研活动观察统计来看，教师注重数学情景的设计，进行新知的导入，注重数学例题的教学，注重知识的拓展与提升，却忽略了对学生数学阅读技巧的引领和培养，并且我发现，在数学课堂中学生的数学阅读活动，教师脱离了教材，脱离了生本，以至于教师只注重教学方法而缺失了学习方法的指导，导致学生的数学阅读能力相当薄弱，在解题过程中无法正确领会题意，审题常常出现偏差，以至于数学成绩滞缓，使学生对数学学习产生畏难情绪，甚至失去学习数学的兴趣。

二、初中学生数学阅读能力培养的策略

（一）把握数学特点，领会数学阅读的技巧

1.引导学生感知认读“数学语言符号”

每个数学概念、符号、术语、公式、图表不仅具有精确的含义，而且有着特定的内涵与外延，有着高度的概括性和抽象性。因此，教师在指导学生进行数学阅读时，应注意文字、数学符号、术语、公式、图表的感知与认读，领会每个数学概念、符号、术语、公式等独有的精确含义。

学生学习统计图表时，就要领会图表所蕴含的数学信息，根据图表的知识和图表所具有的信息，进行合理筛选，选择有效的数学信息。这就是学生在感知和认读“数学语言符号”。

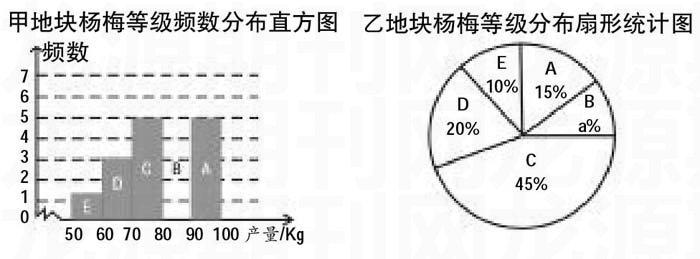
例如：果农老张进行杨梅科学管理实验，把一片梅林分成甲、乙两部分，甲地用新技术管理，乙地用老方法管理，管理成本相同，在甲、乙两块地上随机选取20棵杨梅树，把每棵杨梅树产量分成A、B、C、D、E五个等级，画出统计图。

■

（1）补齐直方图，求a的值及相应扇形的圆心角度数。

（2）选择合适的统计量，比较甲乙两地块的产量水平，并说明实验结果。

学生对于频数分布直方图的阅读，从频数、频率、组中值、样本容量等方面，从而掌握该地块的一些特征数据，进一步与乙地块进行比较。

2.遵循学生的心理规律，激发学生阅读数学的兴趣

初中学生心智和生理处于快速成长期，教师在指导学生进行数学阅读过程中要尊重学生的心理、生理发展规律，选择的数学阅读材料应符合学生的心理发展特点和学生最近发展区，使他们学会主动阅读，轻松获得新知。

例如，教学浙教版七年级上册“2.5有理数的乘方”时，我采用了数学应用的方式创设问题情境：

我提出第一个问题：珠穆朗玛峰是世界最高峰，它的海拔高度是8844.43米。把一张足够大的厚度仅为0.1毫米的纸，连续对折30次的厚度可能超过珠穆朗玛峰。你相信吗？然后师生共同合作探究，把一张纸进行对折、再对折，并在每次对折的过程中进行记录。

然后我提出第二个问题：在上述算式中，同学们发现有一个什么共同特点？学生明确地回答：它们都是乘法的运算，而且因数都是2！这时，我因势利导，引出乘方的概念，从而激发学生进行数学阅读的欲望。

（二）扶本固元，提升数学阅读的维度

1.把握概念内涵，巩固概念阅读

数学概念有其特定的内涵与外延，阅读数学概念时，首先要把握好概念的内涵，才能在阅读中更好地理解概念。

如，在执教浙教版七年级下册“1.5图形的平移”一节时，图形的平移源于物体的平移运动，在指导学生阅读时，我让学生搜寻生活中的实例，让学生认识物体平移的特点：物體各个部分运动的方向相同，而且运动的距离也相同。这样，在概括图形平移这一概念时，学生就能深刻把握“图形平移”的内涵及特点，也为平移的作图和推出平移的性质做好铺垫。当概念生成后，老师可以让学生再举出更多物体平移的实际例子以巩固概念。

2.反思对比例题，引导深层阅读

学生对于教材例题的阅读往往局限于简单的模仿，教师必须从初一年级开始就有意识地对学生进行例题阅读指导。例题阅读一方面要初步学会简单地模仿和操练，更要深层次地理解例题的设计意图和例题之间的比较。

在阅读例题过程中，我指导学生对例题进行反思，老师要从思维发展、问题解决、能力培养等方面进行有意识的指导，逐步提高学生的解题能力。

如，我执教浙教版七年级上册“5.3一元一次方程的解法”第二课时的例题教学：

例题：解方程■-■=1

学生对于例题阅读往往都会掌握解一元一次方程的基本步骤，但是在实际求解过程中，往往会出现以下三种错误：

■■

在指导学生阅读过程中，我从等式性质2出发，让学生思考错误的原因。

3.动手操作，辅助阅读理解

浙教版教材根据《义务教育数学课程标准》的要求，精心设计了课题学习、合作学习、想一想、做一做、探究活动、设计题等单元，让学生在数学学习中构建自己的数学知识和技能，发展数学能力。因此，教师在指导学生阅读过程中，要注重合作探究、操作活动，切身体验数学知识的发生、形成过程。

例如，浙教版七年级下册阅读材料“机会均等”一节：甲和乙两人一起玩掷骰子游戏，游戏规则如下：若骰子朝上一面是数字是6，则甲得10分;若骰子朝上一面的数字不是6，则乙得10分。谁先得到100分，谁就获胜。这个游戏规则公平吗？

经过学生的动手操作，发现该项游戏不公平，从而进一步探究“为何此游戏不公平”的问题。这一“数学化”的活动操作过程，让学生感受概率在实际生活中的应用，也让学生体会活动给予阅读的辅助。

（三）数学思考，渗透数学阅读的思想性

1.培育學生数学建模的阅读能力

数学建模是解决数学问题的主要方法，它主要把实际生活问题转化为数学问题，从而得到解决。教师在指导学生阅读时，要充分引导学生进行“数学式思考，建立数学模型，解决实际问题”。

例如，七年级上册“5.4一元一次方程的应用”例1.某文艺团体为“希望工程”募捐义演，全价票为每张18元，学生享受半价。某场演出共售出966张票，收入15480元，问这场演出共出售学生票多少张？

学生虽然在小学阶段接触列方程解应用题，不过当时的数量关系比较简单，直接列出算式也比较容易。从七年级开始，学生所涉及应用题相对而言数量关系比较复杂，对于问题中含有哪些量？哪些是已知量？哪些是未知量？这些量之间的数量关系又是怎样？这些问题学生在阅读时难以理解清楚。这样，学生对于“列方程解应用题”就产生畏难情绪了。

我引导学生阅读时，帮助学生理清各种数量关系语的切确含义，找出数量关系，从而引导学生进一步考虑设未知数、选择方程这一数学模型列出方程。

2.培育学生形成数形结合的阅读能力

数形结合是解决数学问题的重要手段和思想，教师在指导学生进行阅读的过程中，要经常性地渗透数形结合的思想，从七年级起初的数轴到到八年级的平面直角坐标系，九年级的二次函数等等，都要充分体现“数形结合”的思想。

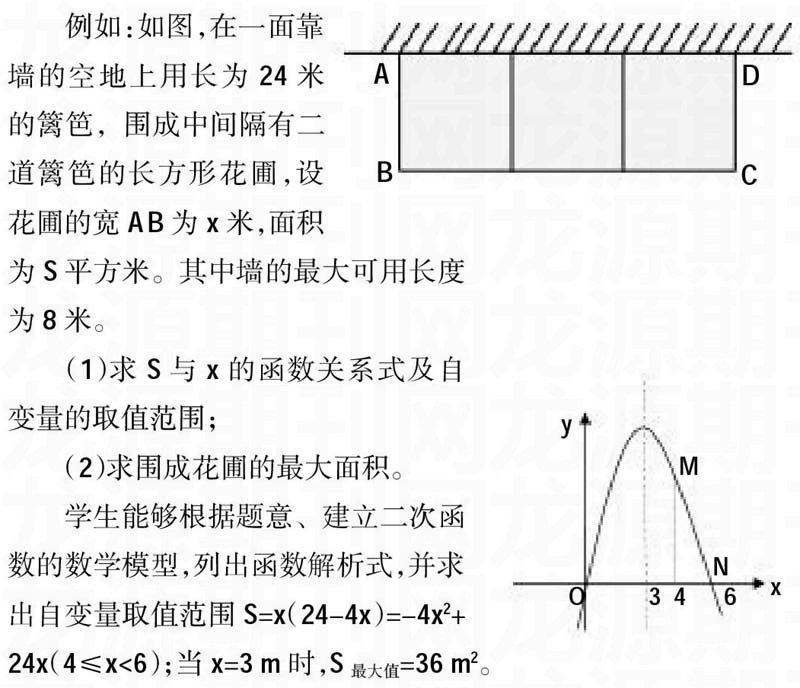
例如：如图，在一面靠墙的空地上用长为24米的篱笆，围成中间隔有二道篱笆的长方形花圃，设花圃的宽AB为x米，面积为S平方米。其中墙的最大可用长度为8米。

（1）求S与x的函数关系式及自变量的取值范围;

（2）求围成花圃的最大面积。

学生能够根据题意、建立二次函数的数学模型，列出函数解析式，并求出自变量取值范围S=x（24-4x）=-4x2+24x（4≤x<6）;当x=3 m时，S最大值=36 m2。

此时，我引导学生在阅读中注意自变量的取值范围，让学生结合自变量的取值范围，画出二次函数的图象，利用数形结合的办法分析“最大面积”，当x=4 m时，S有最大值为32 m2。

在上述问题解决中，一方面学生建立二次函数的模型，解决问题，另一方面在具体函数问题的解决中，采用数形结合的办法，清晰地分析函数的变化特征，从而求出最大值。这是在解决实际问题情景中，利用数形结合、数学建模等多种数学思想，进行数学阅读，更好地把实际问题转化为数学问题。

阅读是学生学习活动的主要活动之一，当然，阅读还涉及阅读具体方法、阅读时间安排、教师如何组织学生对阅读后进行交流、反馈等许多方面，本文主要从数学特点、数学教材阅读、数学思想等方面阐述数学阅读活动采取的策略及方法。笔者以为，让学生真正参与数学阅读、自主参与数学学习活动，这也是教师转变教学手段、学生改变学习方式的很好途径，也是课程改革的一个主要方向。

参考文献：

[1]崔允漷.有效教学[M].南京大学出版社，2009-06.

[2]邓涛.让学生爱上课堂：名师高效课堂的引领艺术[M].西南师范大学出版社，2009-12.

[3]赵国忠.备课最需要什么[M].南京大学出版社，2009.

[4]叶立军.数学新课程理念与实施[M].浙江大学出版社，2005.