以CH2和LiH为例验证分子的洪特多重度规则

2015-10-21谢惠东裴诗恩苏凌峰陈佳媛刘诗咏钟爱国

当代化工 2015年6期

谢惠东裴诗恩苏凌峰陈佳媛刘诗咏钟爱国

摘要：以CH2和LiH分子为例，采用DFT/3-21+G*方法和基组，在垂直和绝热跃迁约束条件下，优化了它们的分子构型;计算了电子组态相同，而自旋态不同的分子（低自旋和高自旋态）物种的最低单点能量。结果发现，无论在垂直还是绝热变化过程，也不论化学键距变化的多少，总会存在分子的洪特多重度关系：高自旋态轨道能总会比其低自旋态的轨道能量更低，也更为稳定。

关键词：密度泛函理论;洪特规则;分子

中图分类号：TQ 624.3 文献标识码： A 文章编号： 1671-0460（2015）06-1200-03

Validation of Hund Multiple Rule Taking CH2 and LiH as Examples

XIE Hui-dong， PEI Shi-en， SU Ling-feng， CHEN Jia-yuan， LIU Shi-yong，ZHONG Ai-guo

（College of Chemical Engineering and Pharmacy， Taizhou University， Zhejiang Taizhou 317000，China）

Abstract： Taking CH2 and LiH as examples，using DFT/3-21+G*， their vertical and adiabatic electronic transitions in the process of configuration were optimized， the lowest single-point energy of species with the same electronic configuration， different low-spin and high spin states was calculated. The results show that， regardless of vertical or adiabatic process of change， and regardless of the length of bond length， there will always be the following relationship： ΔE =ΔT +ΔVee +ΔVne +ΔExc >0.

Key words： Density functional theory; Hund multiplicity rule; Molecular

洪特规则是原子光谱学在量子力学诞生前取得的最后一个重大成就，它是洪特总结从Sc到Ni的原子光谱时得到的规律[1-3]。其最大多重度规则指出，在某一确定组态的光谱项中，自旋量子数S 最大者能量最低。在无机化学课本中则常表述成，电子尽可能分占不同等价轨道，且自旋平行[4-6]。這一规则现已成为讨论核外电子排布的必不可少的基本原则[7]。分子体系总能量由电子总动能、核与电子的总吸引能、电子间的总互斥能所组成。研究结果表明，在某一确定组态一下，各谱项的电子总动能、核与电子的总吸引能都相同，而电子间的总互斥能将随谱项的S值升高而下降，其总结果是多重度大的谱项，分子总能量会最低。这一结论可定性地理解为电子尽可能自旋平行地分布在不同的等价轨道时，同一层次的电子尽量远离，使得电子互斥力较小，体系能量较低。另一方面，洪特规则只要求电子尽可能地占据更多的简并轨道，但并不要求它们的自旋方向相同。洪特规则应用于传统原子轨道图时称为原子的电子排布图。要指出的是，最大多重度规则是总结轻原子光谱得到的规律，它只适用于以静电作用为主的场合，对磁相互作用较强的重原子体系并不适用。洪特最大多重度规则是实验规律的总结，但它却是量子力学计算的必然结果。本文通过对该规则分子体系的剖析，加深对其内涵的理解，有助于正确地应用该规则去解决有关分子中的电子排布问题。但是当改变它们的原子间距后，这一规律是否还是用呢，这是本文需要验证的。

1 计算方法

用 Gaussion 09W 专业量子化学程序包，采用DFT方法，在3-21+G* 基组水平上，选取分子CH2 和 LiH分子体系，对相同电子组态物种应用Gaussion View 构建分子模型，然后提取了高、低自旋态物种的哈密顿算符所对应的分项能量（动能项T，电子-电子之间的相互斥能Vee，核子-电子之间的相互吸引能Vne 以及相关交换能Exc）。然后计算出它们的能量差（ΔT，ΔVee，ΔVne，ΔExc）并且计算低自旋态（以 S=1的单态为例）和高自旋（S=3为例）的最低单点能（ES， ET），和它们的总能量差（ΔE）。在此我们将具有相同电子组态、不同自旋态（单态、三态）物种总能量差可以分解表示为：

ΔE =ΔT +ΔVee +ΔVne +ΔExc，将标题分子中的原子在两种不同跃迁情况（以绝热跃迁和垂直跃迁为例）下的相关交换能差相减，即可得这一物种在该泛函下的交换能差ΔExc。然后分别用该跃迁情况下不同的泛函来进行计算，选取垂直跃迁下最优的泛函，即取同一物种使ΔE 最大的泛函，然后考察它们在不同核间距情况下，于外层电子垂直跃迁过程时的情况。采用量子化学计算方法中的密度泛函方法和量子化学计算相结合，对CH2和LiH的洪特多重度规则作了理论研究。

2 结果与讨论

2.1 分子片在不同泛函下的绝热跃迁下的情况

在量子化学计算过程中，我们曾经应用 DFT 解决了关于自旋多重态的问题。严格的证据早已经证明，基态 DFT 可以延伸到包含不同简并态的自旋多重度领域里面。为了从中找出能较大程度地反映其能量差值升高的变量，分别将 ΔEee、ΔEnn、ΔEne、ΔEk、ΔEx、ΔEc 对 ΔE作单因数线性回归分析。

我们运用Gaussian 09W程序，对不同泛函应用同一物质，对其电子的垂直和绝热跃迁过程，分别进行单点计算以及能量差值计算等，根据得到的数据，分析找出最优泛函，从而确定相同电子组态，不同自旋状态物种总能量差优势项。本项目研究的重点是应用Gaussion View构建CH2和LiH分子模型，用不同的泛函来计算分子的单点能，并且找到其最低单点能所对应的泛函，在这个泛函下构建出同一原子组态，不同原子间距的CH2和LiH分子模型，并且对它们所对应的单重自旋态和三重自旋態进行解析计算。最后在分别在 B3LYP/3-21+G* 和 HCTH/3-21+G* 泛函下用Gaussion 09W软件计算出最低单点能差值ΔE，并作出相关系数R和分能力差值项 ΔT， ΔVee， ΔVne， ΔExc， ΔE 的关系图。

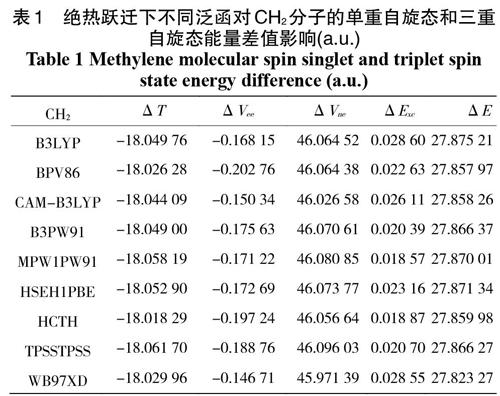
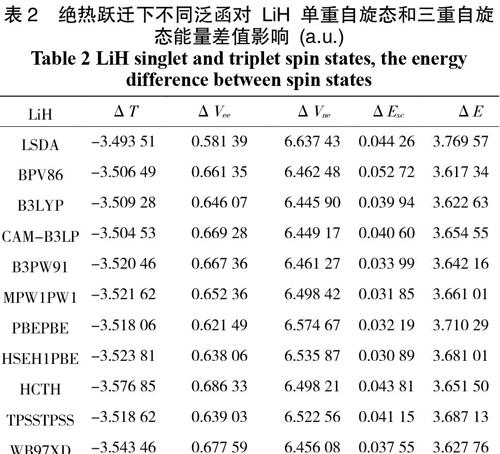
对激发态分子片物种而言，我们首先考虑其外层电子在绝热跃迁下的情况。取分子片内定键距，计算结果位于表1、2中。表1和表2的计算结果可以看出，ΔT 总为负值，对△E起着反向作用;而ΔVee 和ΔExc 总为正值，对△E 起着正向作用;其中最大正面贡献值为 ΔVne，这与Boyd认为 ΔVne 项在起主要正性作用观点相符;但与Slater认为的是ΔVee 项起着主要作用不同。但就CH2分子而言，ΔVee 对结果起着反向作用，而 LiH 的ΔVee 却为正值起着正向作用。最后结果可知这两种分子在绝热激发态下，单重自旋态的单点能始终大于三重自旋态的单点能，因此高自旋态分子相对比低自旋态的要稳定。完全符合分子中的电子的洪特排布规则。

2.2 分子片在不同泛函下的垂直跃迁下的情况

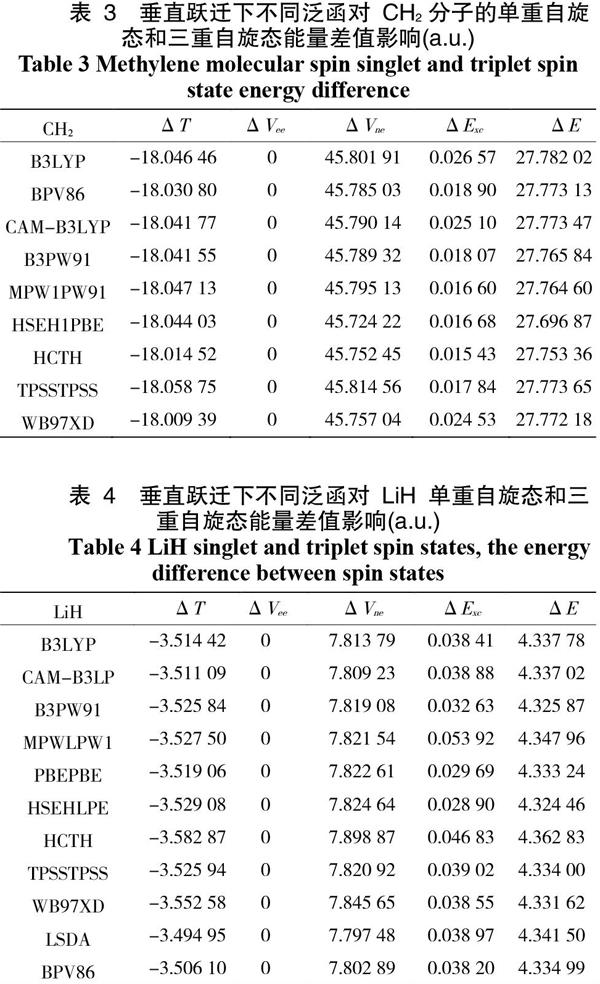
表1和表2的结果仅在绝热下所得，对于相同电子组态的分子物种，还需考虑其垂直跃迁过程时的情况，计算结果列于表3、表4中。表3和表4 的计算结果可以看出，ΔT总为负值，对ΔE起着反向作用;而ΔVne和ΔExc总为正值，对ΔE起着正向作用;其中最大正面贡献值是ΔVne。但在两个表中的ΔVee始终为0，这不同于绝热激发时的结果，这说明了在垂直跃迁的情况下，不管是单重自旋态还是三重自旋态，它们的电子-电子之间的排斥能都一样，不发生改变。同绝热情况一样，ΔE >0，这说明了在垂直激发态下，单重自旋态的单点能也始终大于三重自旋态的单点能，同样证明了高自旋态的分子相对比低自旋态的稳定。而且由表中1-4的数据可知，对于CH2 分子而言，B3LYP是最优的泛函;而对于LiH分子，则 HCTH 是最优泛函。

表1 绝热跃迁下不同泛函对CH2分子的单重自旋态和三重自旋态能量差值影响（a.u.）

表2 绝热跃迁下不同泛函对 LiH 单重自旋态和三重自旋态能量差值影响（a.u.）

表 3 垂直跃迁下不同泛函对 CH2 分子的单重自旋态和三重自旋态能量差值影响（a.u.）

表 4 垂直跃迁下不同泛函对 LiH 单重自旋态和三重自旋态能量差值影响（a.u.）

以 CH2 和 LiH 两个分子物种对洪特多重度规则的验证为例，得出了以下结论：

（1）用能量分解法，在现代量子化学密度泛函理论的基础上，我们选取了两个具有代表性激发态物种CH2和LiH，分别计算了它们在单重自旋态与三重自旋态物种在绝热和垂直跃迁条件下的总能量差值;

（2）考察了11种常见的密度泛函数，如 LSDA、BVP86、B3LYP、CAM-B3LYP、 B3PW91、MPW1PW91、PBEPBE、HSEHLPBE、HCTH、TPSSTPSS、Wb97XD等，对计算两分子总能量差值的影响（计算表明总是大于0）。对于CH2 分子而言，B3LYP是最优的泛函，而对于LiH分子，则 HCTH 是最优泛函;

（3）计算了高、低自旋态物种中的分子在绝热或者垂直变化前、后该物种所具有总能量，并将其能量差值与分量作图进行了比较，得出决定能量差项的优势项和它们的变化趋势。对分子的洪特多重度规则模拟表明：对CH2 和 LiH 两个分子物种，在其高自旋态时具有较低的总能量，而在其处于低自旋时候则具有较高能量。

参考文献：

[1]严成华. Hund 规则的理论解释[J]. 大学化学， 1988 （3）：16-18.

[2]张兴初，胡义华，王小涓. 硫尿嘧啶特征振动的密度泛函理论分析[J]. 武汉大学学报， 2010， 15：45-48.

[3]钟爱国. 原子和分子片的洪特多重度规则的量子化学解释[J]. 分子科学学报， 2008， 58（4）：202-203.

[4]柰文，著. 量子化学[M]. 宁世光，译.人民教育出版社， 1980：319-325.

[5]乔成立，张存华. 小分子的计算化学[J]. 分子科学学报， 2006， 22（3）：213-215.

[6]俞翠英. 計算化学研究进展[J] .榆林学院学报， 2004， 14（3）：48-51.

[7]黎乐民，刘俊婉，金碧辉. 密度泛函理论[J]. 中国基础科学， 2005， 22（1）：112-145.

环保涂料将成企业未来发展重点

5月28日，2015年第九届中国国际水性木器涂料发展研讨会于在北京召开，记者从会上了解到，随着国内产品性能的不断提升，以及上下游联姻的增加，水性木器涂料的市场拓展正全速前行。

中国涂料工业协会会长孙莲英指出，经过近20年的发展，国内生产的水性木器涂料各方面性能已接近或达到国际先进水平，中国水性木器涂料市场已日趋成熟，产量从无到有，技术从粗糙到精细，品种从单一到多样化，各种配套设备都在不断完善。