高中几何中向量的应用探究

巩明珠

向量近代理科中最重要也是最基本的数学概念之一，兼具代数的性质和几何的性质。同时，向量是高中数学最主要的知识点，是学生用来解决高中几何问题的主要手段。

一、高中几何向量的概念

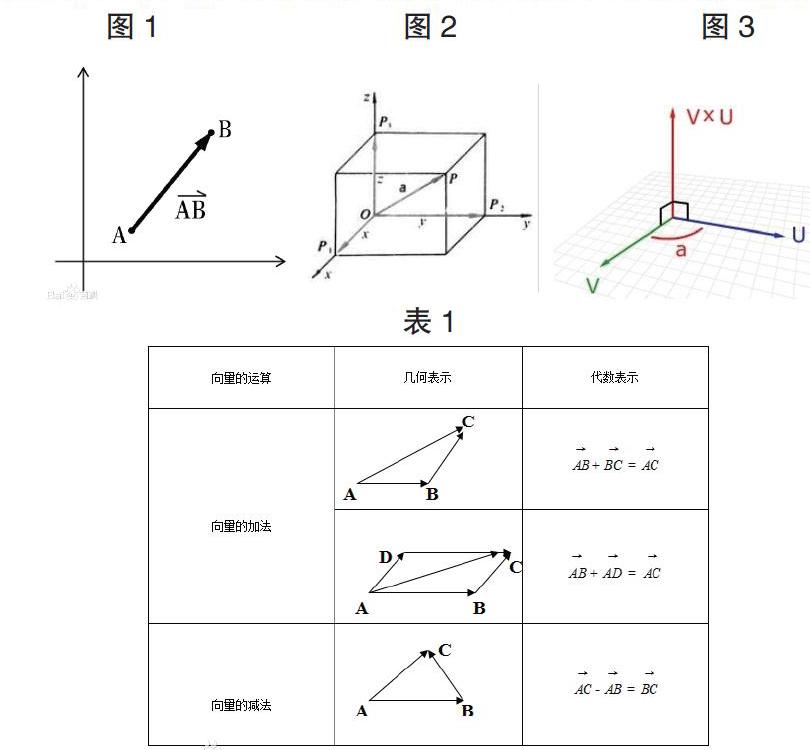
在高中数学的几何中，向量是一种兼具数值大小和箭头方向的几何对象。几何向量，也叫欧几里德向量，是平面向量和空间向量的组成元素。其表达方式是一个带箭头的线段。箭头的指向代表了向量在平面或者空间里的方向，线段的长度则是向量在数值上的大小。一个向量可以有三种表达方式。用小写字母a、b、c…和希腊符号…表示一个向量是代数表示法。用有向线段和单位向量AB来表示一个向量是几何表示法，如图1。用平面坐标OXY或；立体坐标OXYZ来表示一个向量则是坐标表示法，如图2。几何向量的几何性质决定了向量的运算定理。加法、减法、乘法是较为常见的数值运算，如表1所示。数量积是几何数学里特有的一种数乘运算，而向量积则是几何向量独有的运算方式，如图3。

二、高中学生学习几何向量的问题

高中数学对几何向量知识点的考查主要集中在基础知识和应用解题这两个方面。基础知识方面，考查的是向量的基本概念和运算方式，一般都以求长度、求夹角、判断几何形状和垂直、平行等关系的选择题、填空题为主。应用解题方面，考查的是向量知识与其它数学知识的综合应用能力，一般都是以数学知识网络的交汇点来设计解答题的。

三、高中几何向量的具体应用

（一）用向量来解平面几何。平面向量既有大小又有方向，可以进行数值上的代数运算，也可以利用几何性质进行几何演算。

【例1】已知定点A和点B的坐标分别是（-1，0）和（1，0），点P是圆（x-3）2+（y-4）2=4上的一个动点，求2+2的最大值和最小值。

【解题思路】根据题目中的说明，建立起OXY的平面直角坐标轴，将点A和点B标注在坐标上。然后根据圆的几何公式，假设圆心为点C，求出圆心的位置坐标。接着，假设点P的坐标为（x，y），代入公式，求出2+2的长度区间。

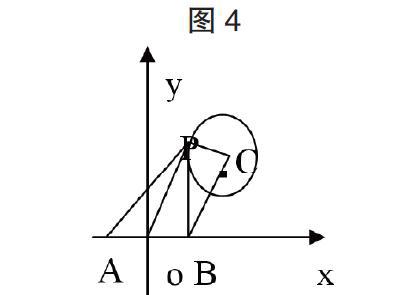
【解题过程】如图4，以x为横轴，以y为竖轴，建立平面直角坐标轴，设圆心为点C，设点P的坐标为 。

因为=（-1，0），=（1，0），所以+=0，·=-1。

由中点公式可以得出+=2，所以，

2+2=（+）2-2·

=（2）2-2（-）·（-）

=42-2·-22+2（+）

=2+2

又因为=（3，4），点P在圆（x-3）2+（y-4）2=4上，

所以=5，=2，=+

得出结论，-≦=≦+

即3≦≦7

所以，20≦2+2=2+2≦100

答：2+2的最大值是100，最小值是20。

（二）用向量来解立体几何

空间向量就是把平面向量及其线性运算推广到了空间，主要用来解决三维空间的图形问题。

【例2】已知四棱锥S-ABCD中，SA=SB=SC=SD=AB=BC=CD=AD，P为SD上的一点。

求证：（1）ACSD；（2）SD平面PAC时，SC上是否存在一个点E，使得BE//平面PAC。如果点E存在，则求出SE：EC的值；如果点E不存在，则说明不存在的理由。

【解题思路】根據题目中的说明，建立起OXYZ的空间直角坐标轴，利用向量的垂直条件·=0，则，可以证明出和这两个向量的平行关系。而要满足线面平行的条件，就要通过运算得出l//·=0的结果。

【解题过程】如图5，连接BD，假设AC和BD的交点是点O，依据题目中的说明可知，SO平面ABCD。所以，以点O为空间直角坐标轴的坐标原点，以OB为x轴，以通过O的AC为y轴，以OS为z轴，建立空间直角坐标轴。证明如下：假设AB=a，可知OS=a，得出点S的坐标是（0，0，a），点D的坐标是（-a，0，0），点C的坐标是（0，a，0）。因为，=（0，a，0），=（-a，0，-a）·=0，所以，ACSD。

四、结语

综上所述，向量是一种带有几何性质的量，是一套具有优良运算通性的数学体系。高中学生在学习几何数学时会遇到对向量的认识不清、忽视向量法的适用性和资料总结严重匮乏这三种问题。因此，高中数学教师在教授学生用向量法快解决数学问题的实际应用中要参照本文列举出的典型题型解题方式，帮助学生理顺题目说明中提供的线索，明晰解题的思路和步骤，条理清晰地解决问题，让学生能够轻易地理解，熟练掌握用向量法解决数学实际问题的具体应用方式。