运用安德森分类二维框架实现教学目标清晰化

【摘 要】 本文运用安德森修订的布卢姆认知领域教育目标分类学二维框架的亚类，分析初一数学教学中二元一次方程组的解法，初步剖析了教学目标不但在知识维度存在缺漏，而且在认知过程维度也存在缺漏，并根据这一分析提出相应的解决方案，运用这一方案进行补救教学，以及在其他班级试教，均获得成功。本研究所得结论：运用安德森修订的布卢姆认知领域教育目标分类框架提炼教学目标并使之清晰化，有的教学目标比较容易提炼，用4类知识×6级认知过程的24格即可；有的教学目标较难处理，需要用Ⅱ亚类×19级认知过程的209格方可弄清楚。

【关 键 词】 安德森教育目标分类 ；布卢姆教育目标分类 ；数学教学

【作者简介】 石皇冠，内蒙古包头市土默特右旗教师进修学校，副高级教师。主要研究方向：小学语文教学、小学数学教学。

一、教师不懂教学目标分识导致学生知识缺漏

人教版七年级数学下册，第八章《二元一次方程组》，教材设计，分为下列几节：

[1]二元一次方程组；

[2]消元——解二元一次方程组；

[3]实际问题与二元一次方程组；

[4]三元一次方程组的解法（选学）。

第[1]节介绍二元一次方程组的概念，第[3]节学习运用二元一次方程组解决实际问题，这些都不是本章的核心内容。本章的核心内容，是学会解二元一次方组的本领。不少同学在学完第[2]节之后，并未真正掌握解二元一次方程组的本领，仅仅达到“半通不通”的水平：如果题目明确提示用“代入消元法”或“加减消元法”解某些二元一次方程组，学生会做；如果题目没有明确提示，学生解二元一次方程组时就会出现问题，该用“加减消元法”的，却用“代入消元法”，该用“代入消元法”的，却用了“加减消元法”。现把我最近深入教学一线发现的问题抄录如下：

[1]该用加减消元法时，却选用了代入消元法，导致过程繁琐。

一位平时数学成绩很不错的同学，解方组

3x+4y=2 ①

2x-y=5 ②

他的解题步骤如下：

由方程②变形可得到方程③：

y=2x-5 ③

把方程③代入方程①可得④：

3x+4（2x-5）=2 ④

3x+8x-20=2

11x=22

x=2

把x=2代入方程②可得y=-1，

方程组的解：

x=2

y=-1

其实，用加减消元法解这个方程组，步骤更简洁：

3x+4y=2 ①

2x-y=5 ②

①+②×4可得：

（3x+8x）+（4y-4y）=2+20

11x=22

x=2

把x=2代入方程②可得y=-1，方程组的解：

x=2

y=-1

[2]该用代入消元法时，却选用了加减消元法，导致计算过程繁难。也是一位平时数学成绩优秀的同学，解方程组

2009x-2010y=1 ①

2011x-2012y=3 ②

①×2011，②×2009，得到新的方程组：

4040099x-4042110y=2011 ③

4040099x-4042108y=6027 ④

④-③，得：

4042110y-4042108y=4016

2 y=4016

y=2008

把y=2008代入①，可得：

2009x=4036081

x=2009

方程组的解是

x=2009

y=2008

其实，灵活选用这两种解法，这道题没必要笔算，口算就能解决。

2009x-2010y=1 ①

2011x-2012y=3 ②

②-①可得方程③：

2x-2y=2 ③

③÷2可得方程④：

x-y=1 ④

④变形可得⑤：

x=1+y ⑤

把⑤代入①可得⑥：

2009（1+y）-2010y=1 ⑥

2009+2009y-2010y=1

2009-y=1

y=2008

把y=2008代入④，可得x =2009。方程组的解是：

x=2009

y=2008

用消元（加减、代入）法解二元一次方程组，这一节教材的教学内容，并未编排“合理、灵活选用两种消元法之一种解方程组”（教材缺少关键的知識点），只编排了“用代入消元法解二元一次方程组”、“用加减消元法解二元一次方程组”。教材中解二元一次方程组的习题18道，其中14道明确提示用哪种消元法解方程组，另外4道题没有提示用哪种消元法，不少老师和同学的理解：没有明确提示用哪种消元法的题目，用哪种消元法解都可以，求出正确的解就行。还有的老师和同学说，不管这法、那法，求出正确的解就是好法。笔者以为，养成这种思维习惯，学不好数学。

凡是认真学过布卢姆教育目标分类学（认知领域，安德森等2011修订版）的数学教师或研究人员，很容易发现这个问题。教材编写属于宏观教学设计，编写教材的专家，至少应该掌握布卢姆教育目标分学（2001安德森等修订版）的基本常识。由于教材编写人员不懂教学目标分类，导致教科书存在知识点缺漏。如果一线教师掌握了教育目标分类学基本常识，就会想办法弥补教材缺陷，防止学生知识点欠缺。

二、教师粗略学习教学目标分类无法解决问题

有的教師和研究人员，学过布卢姆教学教育目标分类学，可他们学的是1956版的中译本。1956版的分类学表，还没有强调知识分类，只有掌握水平（也称认知过程）一个维度。1956版分类学，主要是为教育测量而研制的。即使学过1956版分类学，也无法弄清本文所说的知识点缺漏，需要学习安德森等主持修订的2001版。这一修订版，增加了知识分类，把学生要学的认知领域的知识按照由具体到抽象的顺序分为四类：1事实性知识；2概念性知识；3程序性知识（方法步骤类）；4反省认知知识，详见本文表一。一般人学习布卢姆教育目标分类学二维框架，往往停留于“表一”这个地步。把上面初一学生学习二元一次方程组解法的两个教学目标补充完整，整理成三个教学目标： [1]能用“代入消元法”解二元一次方程组；[2]能用“加减消元法”解二元一次方程组；[3]恰当选用两种解法之一种解二元一次方程组。

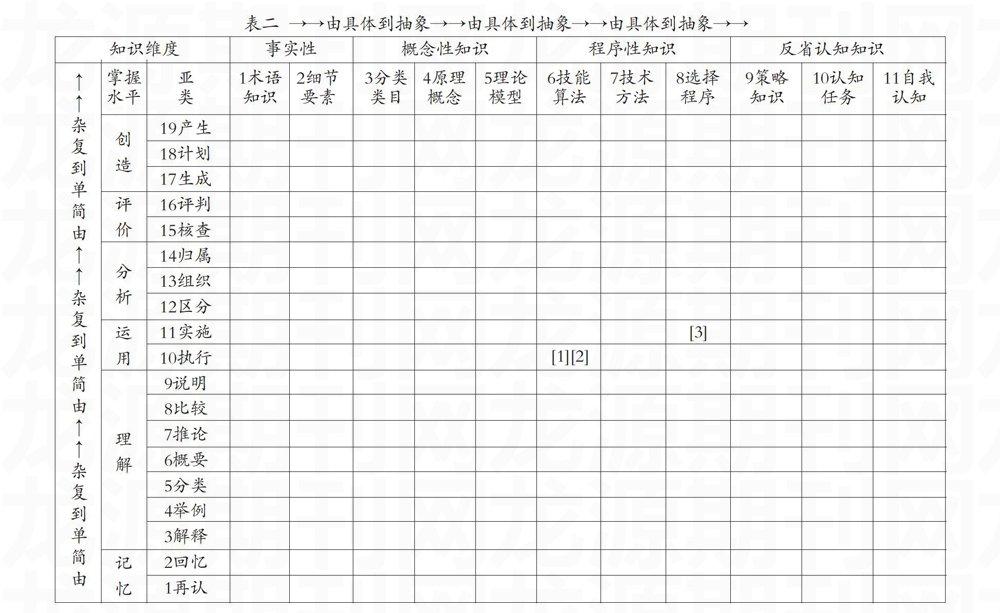
如果期末考试只针对 [1][2]两个教学目标进行评估，不涉及教科书之外的知识点，比如目标[3]，面向初一学生的数学教学就不会因为期末考试而出现“应试教育”。实际上，老师除了教教材、用教材教之外，还要拿来模拟试卷进行“综合演练”，以弥补考试和教科书在知识点和掌握要求之间的差异。负责考试的命题专家，负责课堂教学评估的学校领导和教研员，负责课时计划、实施教学过程的一线教师，负责编制课本的教材设计专家，如果能在同一个平台上对话，特别是能在修订之后的教育目标分类学二维框架（详细的亚类表，见本文表二）内寻求教学目标、教学过程、教学评估三者之间的高度一致性，那就不会出现目标、教学、评估三者之间各自为政、各行其事、互不通气、藩镇割据的混乱局面，坚决杜绝三者“各吹各的号、各唱各的调”，三方面力量力争按同一旋律“唱同一首歌”，初一年级及其以下何来应试教育的痛苦？教育管理，首先管的就是教学目标、教学过程、教学评估是否在教育目标分类学框架内达到高度一致。

把上面三个教学目标置于二维（度）分类框架的表一中，在知识分类的横向坐标上，目标[1][2][3]都属于程序性知识（技能、方法、步骤类），目标[3]和目标[1][2]在知识类别上难以进行细致的区分；在掌握水平的纵向坐标上，目标[1][2][3]都要掌握到应用水平，目标[3]和目标[1][2]难以进行细致的区分。也就是说，仅仅用四类知识和六级掌握水平组成的二维（度）框架表（24格）难以把这三个目标清晰化，目标[3]和目标[1][2]混在一起，没有凸显出目标[3]的特点，没有凸显出目标[3]的独立存在，目标[3]依然处于可有可无的尴尬地位。也就是说，学习布卢姆教育目标分类学（认知领域），停留于4类知识×6种掌握程度这一水平，也就是在24个格子中给教学目标定位，还远远不够。要再进一步，学习每个大类之下的亚类，也就是要学习由11种知识亚类和19种掌握水平亚类所组成的二维（度）框架表，在209个格子中给教学目标定位，详见表二。

三、目标清晰化需要深入学习分类框架的亚类

使用“表二”这样的详细表格，就能把目标[3]和目标[1][2]进一步清晰化。目标[3]和目标[1][2]虽然都属于“程序性知识”（技能、算法、步骤类），但如果深入到11个亚类来细加区分的话，知识类别有差异，抽象程度也不同。在横坐标上由具体到抽象的11类知识中，目标[3]属于第8类，就是“在什么情况下选用哪种解法”；而目标[1][2]则属于第6类，即“特殊学科技能、算法的知识”。目标[3]和目标[1][2]虽然都应该掌握到“应用水平”（分为执行和实施两个不同的程度），在纵坐标上由简单到复杂的19类掌握水平中，目标[3]属于第11级，即“实施”；而目标[1][2]则属于第10级，即“执行”。目标[1][2]只要达到能执行的水平即可：学生能按要求会用代入消元法解方程组，或者能按要求会用加减法消元法解方程组。笼统地说目标[3]掌握到“应用”水平，是不行的。说目标[3]掌握到第10级的“执行”水平，是不对的。目标[3]应该掌握到第11级“实施”水平，也就是说，要在不同的情境下，合理、灵活选用代入消元法或者加减消元法解二元一次方程组，才算掌握了目标[3]。虽然同为安德森修订的布卢姆教育目标分类学二维框架表，详细的209格和粗略24格的不同。有些教学目标，在24格中找到恰当位置即可实现清晰化；有些教学目标，必须在209格中找到恰当位置方可实现清晰化。这就要求相关专业人员在初步掌握24格如何使用的基础上，进一步掌握209格的使用方法。不但要熟悉四类知识的区别，还要进一步熟悉11个亚类之间的区别；不但要熟悉六级掌握水平之间的差异，还要进一步掌握19级掌握水平之间的差异。

四、依据目标清晰化的研究结果弥补教材缺漏

通过教学目标清晰化，知道了学生应该掌握的关键知识点和教材的缺漏，教师就要弥补教材缺漏，补充一节教学内容：“合理、灵活地选用代入消元法或者加减消元法解二元一次方程组”。为了实现目标[3]增加一课时，有的老师容易上成练习课，希望学生在大量的解题实践中感悟解题窍门；有的老师容易上成“一言堂”，教师讲解自己的解题心得，学生听完之后做练习，课后交作业本，教师批改；有经验的老师一般会上成指导课，老师精选典型题目，学生练一道，教师点拨一下，学生在解题实践探索和教师指导中掌握窍门。上述三种情形，比较理想的是第三种。但是，第三种情形下，学生掌握的“遇到不同题目如何选择解法的窍门”可能是“茶壶里煮饺子”——有东西倒不出来——知道怎么做，但是难以言表。如果是默会的规则，可能就是这样。比如，六、七岁儿童说话（特别是讲故事）大多符合语法规则，说明他们能在符合语法规则的前提下生成一大段（篇）话。但是，如果要求六、七岁儿童把他所掌握的语法规则说出来，恐怕办不到。这种会用不会说的规则，就属于默会规则。目标[3]不应该是默会规则。如果目标[3]也按默会规则传授的话，教学效率不会高。

把目标[3]所蕴含的规则用精煉通俗的言语陈述出来，是提高教学效率的关键所在，也是补充教学内容的关键。既然是确定的知识点，已经运用教学目标分类工具把它清晰化了，而且又不属于默会规则，最好也把它明确化。我建议目标[3]的知识点这样来陈述：

[1]一审题：一般的简单题目，初步审题，即可确定选用加减法消元简单，还是选用代入法消元简单。这一步简称“一审择法”。

[2]二变形：如遇稍复杂题目，一审难以确定该选哪一种解法，就开始思考通过方程变形来整理、简化方程组。变形的依据是方程同解原理。这一步简称“二变整理”。变形的结果，便于下一步加减消元。

[3]三加减：在整理变形的基础上，两个方程即可进行加减运算。这一步简称“三步加减”。初步的加减运算如果能消元，即可接着解方程。如果只是化简了方程，还不能消元的话，就转入下一步。

[4]四代入：第三步如果仅仅是化简出非常简明的方程组，而没有消元的话，就要考虑选用代入法消元了。简称“四步代入”。

这四步用简练的词句表达，就是“一审、二变、加减、代入”。 学习这种程序性知识，一般要遵循一个大体顺序，即两个阶段：“陈述性知识学习阶段→程序性知识学习阶段”。之所以要把这四步操骤写成白纸黑字，就是为了让学生准确理解。之所以要提炼成简洁的词句，就是便于学生记忆。理解了，记住了，便于学生结合具体的题目练习尽快掌握这个窍门。

教学建议：教师借助一道典型例题，先让学生理解“一审题、二变形、三加减、四代入”。也可以把上面的四部全文印发给学生，学生自读，自读过程中，学生有充分的自主理解时间。再花一分钟时间熟记这12个字的口诀。接下来，教师出示一道精选的习题，学生练习，教师及时提供反馈信息，同时对个别学困生给予必要指导。教师可以在整节课上多次重复这个环节，直至下课。也可以留出一定时间，鼓励学生编题，由班内同学解答。设计这个专节的目的，是让学生从另一个角度熟悉二元一次方程组的特点，更好地掌握目标[3]。

上述研究结果，用于补救教学，以及在其它班级试教，均获得成功。如果教师不懂得弥补教材的知识点缺漏，不专门设计一节课进行该知识点教学，部分学生也可能掌握目标[3]，但那是在做过好多模拟试卷订正错题的基础上掌握的。目标越模糊，掌握技能某项技能需要的练习量就越大。

五、结束语

教学目标清晰化，仅仅掌握1956版的教育目标分类学（一个维度）还不行，掌握2001版的4类知识×6级掌握程度的二维框（24格）架还不够，要掌握11（亚）类知识×19（亚类）级掌握程度的二维框架（209格），才能把教学目标清晰化。这种目标如果不是默会的规则，一般要用清晰简练的书面词句陈述出来，白纸黑字放在显眼处，不能让学生在黑暗中揣摸、体会、感悟，短短四十分钟会很容易被这种冠冕堂皇的事情浪费一大半。教学过程一般分为两个阶段：陈述性知识学习阶段→程序性知识学习阶段。必须经过多次练习，特别是变式练习，才便于掌握教学目标。下课前，应该有课堂教学评估，设计几道难度和课堂练习相同的题目，考一考学生，看看每生解题正确率有多高，课堂教学目标是否实现。运用这个分类框架，可以把教学目标、教学评估、教学过程三者高度统一起来。2001修订版是安德森等三位课程与教学专家、三位教育心理学专家、两位测量评价专家跟有经验的中小学教师合作多年集体完成的。把教学目标、教学过程、教学评估三者高度统一，正是修订工作的意义所在。如果编教材的专家、上课的老师、评课的教学管理人员和教研员、考试命题的测评专家都掌握了这个教育目标分类框架，这三方面力量就有了真正的对话平台，克服应试教育的弊端就有了可能。否则，这三方面专家在教学研讨活动中永远是“鸡同鸭讲”。