在中职数学教学中渗入美学教育的策略

王春勇

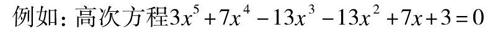
【摘 要】阐述数学中美的现象和美的规律，讲解在中职数学教学中渗入数学美的几种方法。通过展示数学美，发现深层的数学美，进而提升学生的审美能力，引导学生将数学中美的规律、原理应用于解题实践之中。

【关键词】数学  简单美  内涵美  对称美  统一美

【中图分类号】G  【文献标识码】A

【文章编号】0450-9889（2015）12B-0117-03

纵观古今中外的历史，美育对于人类社会的发展起着必不可少的推动作用。数学是一门研究数量、结构、变化、空间以及信息等概念的学科，从某种角度看，它属于最基础的科学，蕴含丰富的内涵与美。现代科学越来越进步越多元，但是我们也发现，几乎所有的自然科学专家在数学方面都有着杰出的数学成就，其中就包括很多诺贝尔获得者。前几年，日本研究者把祖冲之发现的密率化为混小数后，再把每个数字作为对应的音符，通过乐器来演奏，竟然发现这是一首陶醉人的乐曲。究竟是什么让人们感觉到数学如此美妙呢？庞家莱的一句话给出了答案：“在实际解题、证明过程中，给我们以美感的是各部分之间的和谐、对称，恰到好处的平衡。”

数学是一门基础学科，在中职学校也是一门必修课，学好数学是学好其他专业课的前提。然而，当前的中职学生对数学的学习兴趣不高，所以，为了激发他们的学习兴趣，挖掘学生在数学方面的创造潜力，培养他们的逻辑思维，在数学教学中把发现数学美与数学教学融合，可以较好地相互补充。下面对数学中展现着怎样的美与如何进行数学教学中的美育教育这两个问题加以探究。

一、数学中的美

著名的数学家罗素说：“数学如果正确看，不但拥有真理，而且具有至高的美。”数学美指的是存在于数学中的美的现象和规律，它的内容是非常丰富的。比如，概念的简单和统一相结合，结构的协调和对称相结合，命题的概括与典型性相结合，语言准确与特殊相结合等，都是数学内在美的具体内容。

（一）简单美

简单是数学美组成的基本内容。从数学理论的逻辑构造而言，数学美的简单性往往包括两个方面的内容：一理论结构简单性，其概念独立、简单和明确，以最少的公理、公式来建立理论;二理论的表现形式简单性，以简单的方式表现现象的本质，使定理和公式更加简单明晰。

数学的简单美体现在它的方法上。一个美的数学方法和证明，往往都包含着极其简单的涵义。比如希尔伯特解决果尔丹问题的存在性所使用证明方法，就是数学方法简单美体现的一个范例。希尔伯特的方法是简单和深刻的，正因为这样才使它能应用到抽象的代数中，并把群、环、域的抽象理论提高到至高的地位。

数学的简单美也体现在它的形态上。数学的形态美是数学美的外部表现的形态和形式，是数学定理、定理外在结构中呈现出来的美。塔的主要特征，体现在于它的简单性。如，牛顿用一个简单的公式F=ma，就概括了力、质量、加速度之间的定量关系;爱因斯坦也是用一个简单的公式E=mc2，就揭示了自然界的质量和能量的转换关系。这里F=ma和E=mc2就外在形式而论，都是非常简洁的，都是为数学形态美的表现的范例。

由此可见，数学中的简单美以其极简洁的形式和思想，把大量复杂的事实变得简单而深远，充分显示其作为一门自然科学的理论美。

（二）对称美

毕达哥拉斯学派认为，一切空间图形中，最美的是球形;一切平面图形中，最美的是圆形。这样的称赞，原因在于球形、圆形都具有强烈的对称性和匀称性。众多的几何图形、代数中的方程式也都表现了一种对称美。

例如：高次方程3x5+7x4-13x3-13x2+7x+3=0

方程中首尾对应的项的系数是对称的，这一特征为求解高次方程带来了极大的方便。

数学中体现对称美的地方很多，这种对称的美也不但只有数学家独自欣赏的，人们日常生活生产中也常常追求对称美。如我们看到的对数螺线、烟花，只要你知道它的一部分，就可以推断出它的全部。

这一切表明，对称性在数学中作为一种方法、作为一种审美，发挥着巨大的作用。

（三）统一美

数学中的统一性代表了客观世界的一种和谐，它实质上是一种理性统一的艺术结晶。从《几何原本》、微积分的发现到近代科技数学的成果，无一不体现数学的统一之美。

例如，抛物线方程：y=ax2+bx+c （a≠0），当b=c=0时，得到方程y=ax2 （a≠0），它可以用来描述自然界的质能方程（E=mc2），也可以用来描述物理学中的自由落体现象（），还可以描述几何学中的圆面积计算公式（S=πr2）。还有很多这类的例子，无法想象万千的事物规律统一于一个相同的数学式子，毫无疑问，这彰显了数学的伟大和它的完美性。

例如，中职数学中，圆、椭圆、雙曲线、抛物线简单地统一于极坐标方程：

其中e是离心率，e的变化表达了差异的本质。

统一性不仅仅是一种数学美的特征，它实际上表现了一种数学的本质，如果把数学看作是一种理性建构的世界，那么统一性就是人们理性世界中的擎天石。

（四）数学内涵的美

数学具有一种理性美，内涵的美。人们都知道数学和物理是一对孪生姊妹，数学和物理的结合点是美的叠加。下面我们举几个例子，看看它的美之所在。

例如，中职数学解析几何中的椭圆，是人们司空见惯的曲线。但当人造地球卫星进入轨道时的水平速度大于 7.9 千米/秒而小于 11.2 千米/秒时，它绕地球运动的轨道是一个椭圆，且地球恰好处在这个椭圆中的一个焦点上。

又例如，一元二次函数y=ax2+bx+c。这也是中职数学中常见的函数，学生在学习这个函数时并不感觉到美的存在。但是如果把它跟初速度不为零的匀加速直线运动的公式结合起来，一元二次函数的内涵美就体现出来了，它客观地把匀变速直线运动的自然规律表现出来。

这一公式完美地体现了 S （变量）的大小与时刻 t 的关系。这就是一元二次函数对作匀变速直线运动的物体的运动规律的描述。

通过以上事例，我们可以知道，数学和美学是紧紧相连的，它正以一种独特的方式来诠释美，它把美学刻画得深刻透彻。这正是数学内涵的美的规律体现。

二、在中职数学教学中如何运用数学美

数学充满丰富的美，数学美常常能对人类进步产生巨大的推动力。它能够激发人们产生创造发明数学的激情，启发人的智慧，从而提高人的探索问题和解决问题的能力。在实际的数学教学中，要使得学生更多地理解和认知数学的美，使他们在课堂中潜移默化地产生对数学美的追求，进而促进他们在数学方面潜能的发展。下面就多年来的教学实践，谈谈在数学教学中如何进行美育教学。

（一）在教学中展示数学之美，提升学生感知美的能力

我国著名的数学家徐利治教授曾说过：“学生的学习应该是主动的、富有美感的智力活动，学习材料的兴趣和美学价值乃是学习的最佳刺激，强烈的心智活动所带来的美的愉悦和享受是推动学习的最好动力。”学生只有在学习中经历了发现、感知、体验和运用的过程，才能真正地感受到数学美的力量，得到知识和心灵提升的双重满足。

课堂中可以借助直观的模型教具，如圆柱、圆锥、球、棱台等，让学生在直观中欣赏数学的美;也可以借助动画或者多媒体技术，领会到一些数学图形的产生过程，欣赏到数学的图形美。这种表象中的美可以加深学生对具体知识特征的认识，在潜意识中培养了学生的审美感觉。

让学生在相关概念、公式的学习中感受美。例如，物理中的许多公式，如上面所讲到的力学公式F=ma，质量公式E=mc2。这些都不失为数学形态美的范例。在课堂学习中运用美的思想进行扩展和补充，使之和谐统一。久而久之，学生的审美感觉就会潜滋暗长。

（二）在实际教学中深入挖掘数学美，把趣味学习和美学教育相结合

在中职数学教学中，在正确掌握数学概念、理解数学知识的基础上，引导学生挖掘数学中的美学因素，应用“补美”方法探索解题技巧。

例如，当 n 是自然数时，“n！”表示从 1 到 n 的 n 个自然数的乘积，即 n！=1×2×3×…（n-1）×n。而当 n=0 时，“0！”显然没有意义，这怎么办呢？

为了使 m=n 时，公式仍旧成立，就必须补充规定 0！=1。补充规定 0！=1 是补美思想的体现，同时，保证了更高层次中的和谐性。学生在学习这个公式的过程中获得了数学和谐美的感受，这既启发了学生的思维，又使得学生对知识深化了理解。

把数学的美作为一种引导，往往能促进学生对知识的理解与巩固，使得学生的学习充满了趣味性。让学生在学习过程中，不但感受了数学美，而且能够创造性地解决数学中的问题。

（三）在教学中培养学生探索与创造数学美的能力

学生在解数学题时，常会遇到数量和图形关系复杂的情况，这种时候学生比较难发现题目中蕴含的数学“美”的形式，这时我们引导学生依据数学问题的本质特点，按照数学的规律来凸显数学之美，从解决数学问题。

例如，请证明，在任意三角形中，三个内角的平分线连乘积小于三条边的连乘积。

证明  如图所示，三角形的三条边分别为AB、BC、AC，取△ABC的外接圆O。延长三条角平分线分别交圆O于点M、N、L，连接BM、CN、AL。

∵∠BAM=∠MAC，且∠M=∠ACB

∴△ABM∽△ADC

∴

∴AB·AC=AD·AM>AD·AD=AD2   ①

同理

AB·BC>BE2    ②

AC·BC>CF2    ③

①②③三式相乘得到

（AB·BC·AC）2>（AD·BE·CF）2

∴AB·BC·AC>AD·BE·CF。问题解决。

解决该数学问题的核心在于通过辅助线关系找到三角形相似性这一过渡过程，这过程其实就是设计一个“美”的途径来达到“美”的解题结果。这样既创造了“美”的形式，又为学生解题提供了途径。

对学生而言，解数学题是一个获得探索愉悦的过程，只要他们通过正确的方式和思维逻辑去探索，最终会获得正确的答案。在這个探索的过程中，发现数学美的能力起着关键的作用。学生把题目信息和数学审美情感结合起来，就会激发他们的灵感，使得他们能够迅速准确地找到突破口进而顺利作答。

数学中的美是千姿百态、丰富多彩的，充分领略和认识它的美，能够使人获得赏心悦目体验，并产生美的情怀和智慧，能够使得人类的生活获得巨大的改变。通过在中职数学课堂中渗入和展示更多的数学美，抓好学生审美感知能力的培养，学生的智力和情趣就能够得到很好地开发。

【参考文献】

[1]张奠宙.数学的明天[M].南宁：广西教育出版社，1999

[2]杜瑞芝.数学家传奇：徐利治王梓坤朱梧槚.[M]大连：大连理工大学出版社，2013

[3]方可，李瑾.议数学教学中的美学教育[J].河南教育学院学报（自然科学版），1997（3）

[4]张丽娟.“数学美”浅析[J].数学通报，2004（4）

（责编 卢建龙）