基于海事规则的水面无人艇动态障碍规避方法

杜开君，茅云生，向祖权，周永清，宋利飞，刘 彬

(武汉理工大学a.高性能船舶技术教育部重点实验室;b.交通学院，武汉430063)

基于海事规则的水面无人艇动态障碍规避方法

杜开君a，b，茅云生a，b，向祖权a，b，周永清a，b，宋利飞b，刘 彬b

(武汉理工大学a.高性能船舶技术教育部重点实验室;b.交通学院，武汉430063)

针对水面无人艇对探测到的电子海图上没有标示的动态障碍物的规避问题,提出符合国际海上避碰规则公约的规避方法,将动态障碍物某一运动时刻转换为相对无人艇瞬时静止的状态,对避障模型进行实时计算;并通过粒子群优化算法解算出无人艇进行避障所需的最优航速和航向改变量。仿真实验表明,该方法可得到合理的规避策略,有效地完成动态障碍物的规避任务。

水面无人艇;动态障碍物;粒子群优化算法;路径规划;海事规则

水面无人艇(unmanned surface vehicle,USV)作为一种无人海上航行器,是惟一一种可以在水上、水面、水下同时发挥作用的无人运载平台［1］。在航行过程中,水面无人艇处在不可预见的动态的海洋环境中,障碍物很可能出现在已经规划好的全局路径上,而AIS或航海雷达并没有探测到,电子海图上也没有标示障碍物及其运动信息。为了保证无人艇能够快速、安全地到达目标,需要对使其处在危险状况下的动态障碍物进行规避,这正是决定无人艇智能化程度高低的关键技术之一［1-5］。在分析各种无人艇障碍规避方法的基础上,提出基于海事规则的水面无人艇动态障碍规避方法。该方法根据国际海上航行规则公约将碰撞情形划分为追越、正面相遇、交叉相遇3种局面;引入极坐标系下的粒子群优化算法,通过改变无人艇航速和航向,实现规避动态障碍物的目的。

1 极坐标系下的建模

常用的两种平面坐标系为笛卡尔坐标系和极坐标系。笛卡尔坐标系在建模时具有局限性,如只能向前走,容易掉入陷阱;而极坐标空间则对长度和角度敏感,可以将各维分量与路径处的期望航速和航向关联,并且便于描述障碍物信息。所以,采取极坐标系进行建模。

极坐标系下的起点和终点分别为在全局规划路径中选取的子目标段的起点和终点。这两点的连线为极坐标系的极轴,起始点为极点,逆时针方向为正。

真实环境下,障碍物的形状各种各样,通过雷达扫描出来的雷达图像或通过声呐、传感器得到的障碍物形状会很复杂,直接对这些未经处理的障碍物形状进行避障,其计算过程往往会代价高昂,导致计算时间增加。为了缩短计算时间,在进行路径规划之前,需要对障碍物进行包围体处理,使障碍物形状得到合理的简化。

国内大部分学者对障碍物包围体的处理仅采取圆形包围处理,未充分考虑到海面上运行的船舶均为长宽比较大的障碍,仅采取圆形包围会损失大量可行区间,从而造成避障策略不合理。这里对障碍物的包围体处理包括两种方式。

1)对长宽比较小(取小于2∶1)的障碍物来说,采用圆形进行障碍包围,不会损失太多的可行路径;且极大地简少了计算量,可有效缩短计算时长。外包圆具体取值方法为:其直径取障碍物所有顶点连线的最大值,即

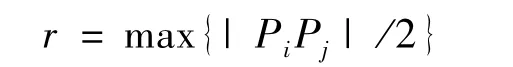
式中:P——障碍顶点且(i,j∈N,i≠j),圆心即为最大连线的中点。

2)对长宽比较大(大于2∶1)的障碍物来说,将障碍物进行更贴合实际形状的模拟(即有向包围盒,OBB［6］)。虽然增大了计算量,但采用此方法,可得到更多的有效路径区间,产生更优的避障路径,使得避障能耗更小、续航力更久。

无人艇在海面航行过程中,会存在许多不确定性因素,如障碍物运动的不确定性、无人艇本身运动的不确定性、执行机构运行时的不确定性、无人艇自身定位和对障碍物进行探测的系统也不可避免地存在误差等。为了简化计算,将水面无人艇作为一个质心处理,所以还需要对障碍物进行膨胀建模。

2 动态障碍物避障模型

无人艇和圆形动态障碍物当前时刻的几何模型见图1。图中:VUSV为无人艇的运动速度;VObs为障碍物的运动速度;α为极轴到VUSV的角度,可表示为α=∠(VUSV,ex),其中:ex为极轴;同理β=∠(VObs,ex)为极轴到VObs的角度;θ=∠(LRO,ex)为极轴到无人艇与障碍物圆心连线(LRO)的角度;φ=∠(VUSV,ΔV)为ΔV到VUSV的角度;γ=∠(ΔV,LRO),μ=∠(LRO,tan L),tan L为障碍圆切线。

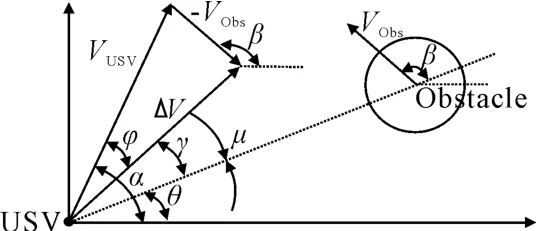
图1 避障模型示意

为使无人艇能在下一时刻避开障碍区间,γ应该取在(LRO-μ,LRO+μ)范围之外的角度。下面将通过求解γ,找到无人艇航速和转向需要满足的条件,以实现无人艇避障。

如图2所示,将ΔV分解为指向障碍物圆心的速度分量ΔV0,和其垂直速度分量ΔVγ。其中ΔV0促使无人艇朝向障碍物运动,ΔVγ促使无人艇逃离障碍物。

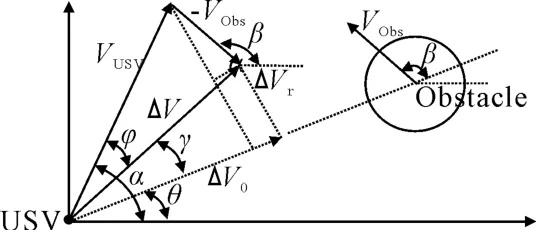
图2 对速度ΔV分解示意图

利用VUSV、VObs、ΔV构成的速度三角形求解ΔVr和γ。

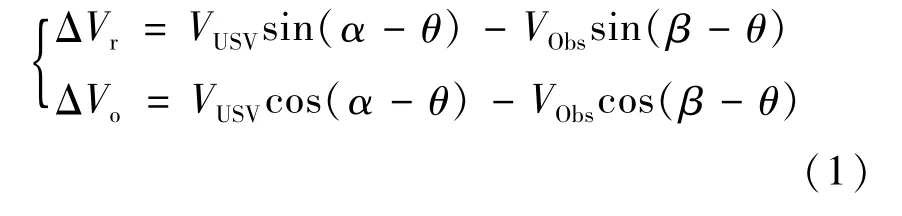
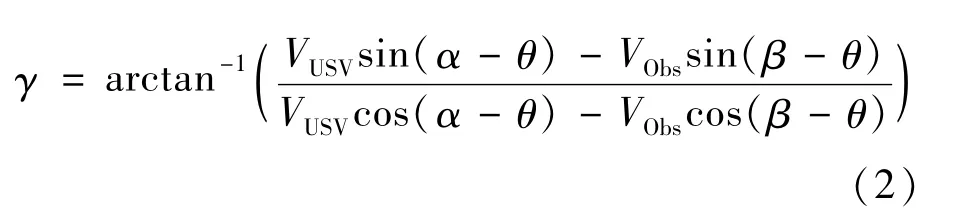
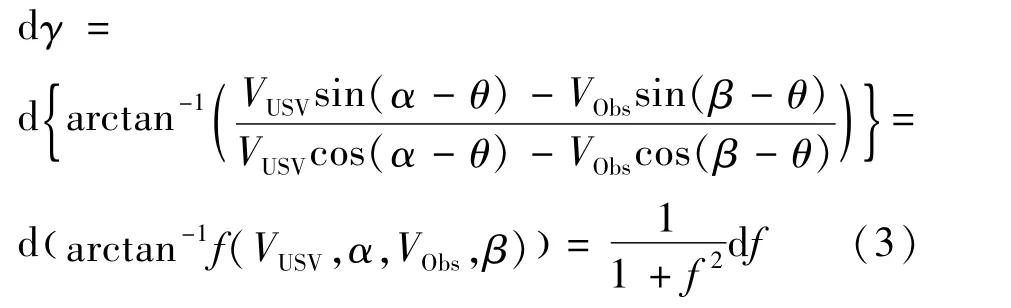
式中:

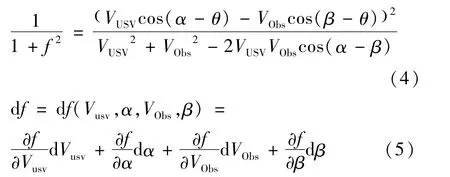
式(5)中,假设圆形动态障碍物运动不发生突变,其运动速度VObs和运动方向β在很短的时间变化很小,可以忽略不计,d VObs=0,dβ=0,则有

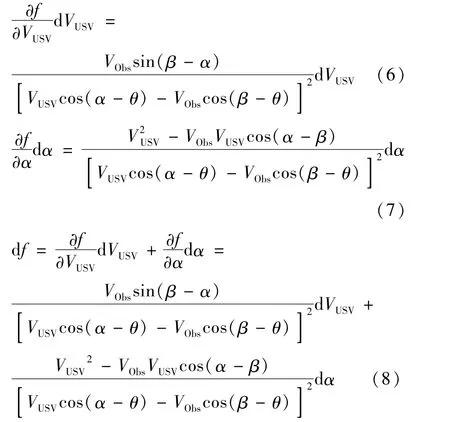
所以式(3)可以转化为用差分形式表示为

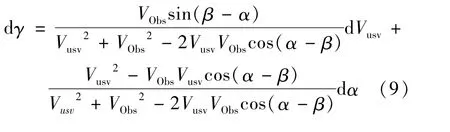
在VUSV、VObs、ΔV构成的速度三角形(如图2)中,存在式(11)关系,其中φ为VUSV、VObs夹角,将其带入式(10),可得到式(12)。

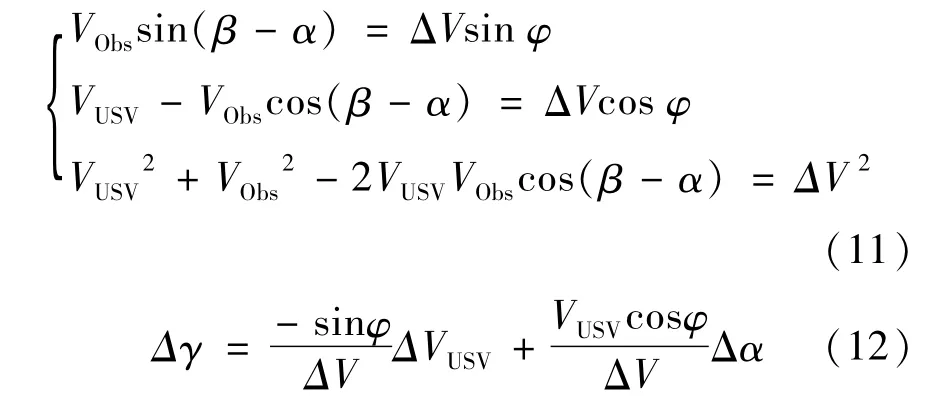
要使无人艇逃离危险区域(LRO-μ,LRO+μ)范围,Δγ需要满足下面的不等式。

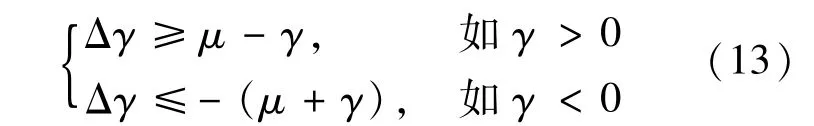
式(12)说明Δγ同无人艇的航速改变量VUSV和航向改变量Δα存在关联,于是避障任务就转化成调整无人艇的航速VUSV和航向Δα。

3 国际海上避碰规则公约的约束

水面无人艇在海面航行过程中,为了避免对海上其他船舶及无人艇自身的安全造成威胁,在进行避障的过程中必须满足相关规则。国际海事组织制定了国际海上避碰规则公约(International Regulations for Preventing Collisions At Sea,1972/ COLREGS),但现在还没有专门的法律法规对无人艇的航行行为做出明确的规定,较合理的解决方法就是使无人艇遵守国际海上避碰规则公约［7］。

国际海上避碰规则公约的13、14、15条分别对无人艇在航行过程中可能出现的碰撞局面:追越、正面相遇和交叉相遇,做出了规定。

图3给出了4种情况的避障模型,障碍物A状态为无人艇在起始点“Start”处探测到该障碍物的位置,箭头为其运动方向;障碍物B状态则为无人艇对该障碍物避障结束时,障碍物所处的位置。

以下无人艇和运动障碍物之间的航向角度差,均以无人艇航向方向为基准(即航向角为0°)进行描述。海事规则冲突情景定义见图4。

1)追越。若无人艇高速航行与障碍物航向角度差在［0°,45°］与 ［315°,360°)之间时,接近危险距离,则无人艇左侧航行。

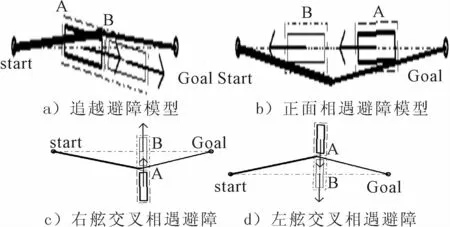
图3 避障模型示意

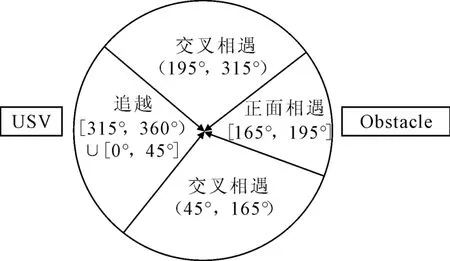
图4 海事规则冲突情景定义

2)正面相遇。若夹角在［165°,195°］之间,接近危险距离,则无人艇应右侧航行,见图3b)。

3)交叉相遇。若夹角在(45°,165°)之间,接近危险距离,则障碍物在无人艇右侧交叉相遇,无人艇应右侧航行,见图3c);若夹角在(195°, 315°)之间,接近危险距离,则障碍物在无人艇左侧交叉相遇,此时无人艇应左侧航行,见图3d)。

4 动态障碍规避

4.1 粒子群优化算法及其适应度函数的确定

粒子群优化算法是一种集群优化算法。假设有一群随机粒子以一定的速度飞行,每个粒子当前自己找到的最优解为Pi,d,全局最优解为Pg,d。其中:d=1,2,…,N。N为粒子群迭代次数［8］。粒子在找到这两个最优解后,按式(14)、(15)来分别更新速度和位置。

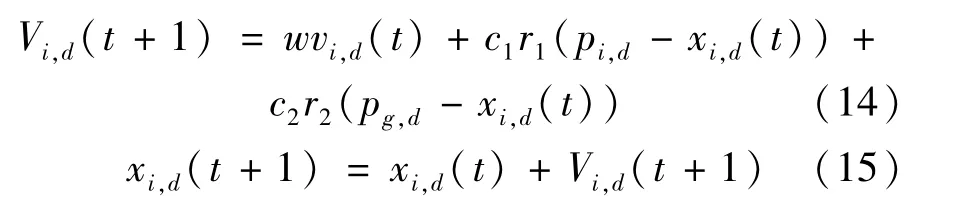
式中:r1和r2为0-1之间均匀分布的随机数。w是惯性权值,文中w的取值选取广泛采用的线性递减惯性权重［9］;c1和c2为学习因子的取值,经多次试验,均取值为2.0。

无人艇在航行过程中,较多使用的是不改变航速,仅改变航向;但在某些情况下还需要同时改变航速和航向的策略,进行避障。航速和航向改变量即为粒子群优化算法的两个维度值,无人艇路径规划问题就可以表达成一个多条件下的目标优化问题。

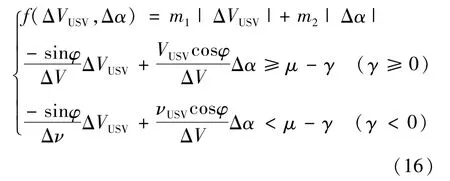
式中:φ、μ、γ、ΔV已知,f(ΔVUSV,Δα)为要实现最优的目标,即为粒子群优化算法中的适应度函数, m1、m2分别为航速改变量和航向改变量的权值。计算得到最优解后还需判断是否在可行域内,即需要满足国际海上避碰规则公约的约束,无人艇最小回转直径的约束,以及不与全局障碍物碰撞的约束。若该段路径中存在多个动态障碍物,则只需对每个障碍物加入式(16)中第2、3个约束即可。

4.2 避障结束点的确定

在对某一子目标段内的动态障碍物实现成功规避后,无人艇需要沿着全局规划路径点继续前行;采用上述的算法得到实现避障后的最优航速和航向,所以还需确定无人艇成功避障时刻的避障结束点。

若障碍物是朝向无人艇运行,在未到达避障结束点之前,障碍物在全局中的极径在不断缩小,见图5a)。图中¯Vusv为经过优化后的无人艇速度、Δ¯V为优化后无人艇和障碍物的合速度。此时避障结束点的选取,可根据在避障模型中,将障碍物视为静止障碍物,以合速度Δ¯V到达障碍物最远端(图中1/4圆弧段处)所耗费的时间t,作为避障结束所耗费的时间;进而转换到全局坐标系下,以此时间段t计算避障结束点的极径值和极角。

若障碍物正远离起始点运行,在未到达避障结束点之前,障碍物在全局中的极径在不断增大,见图5b)。此情况下若还按上述方法进行处理,无疑会造成避障结束点远离本段子目标点。所以在此情况下,设置避障结束点即为本段起始点时障碍物所处位置的极径处为避障结束点处的极径。

综合以上两种求避障结束点的情形,在计算时选取两者极径较小的那一点作为避障结束点。

以上为针对动态圆形障碍物的避障结束点选取方法,动态矩形障碍物的避障结束点选取方法相同。

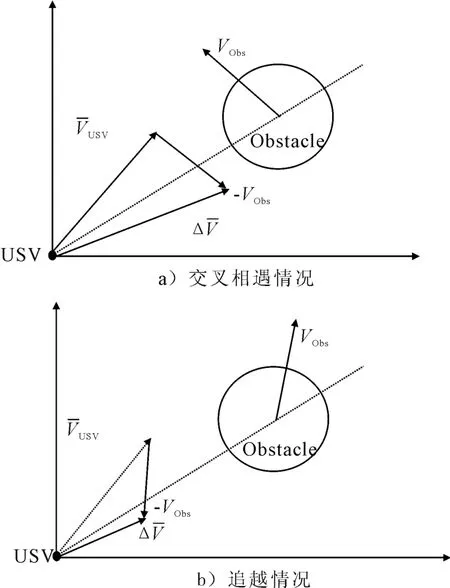
图5 避障结束点示意

4.3 算法描述

结合文中对基于海事规则的水面无人艇动态障碍规避方法,给出该算法的流程,见图6。

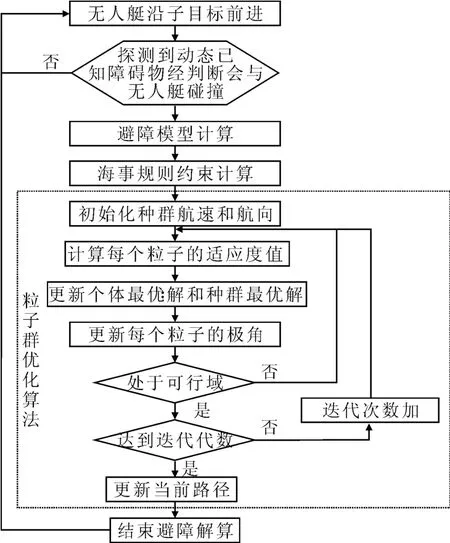
图6 基于海事规则的水面无人艇动态障碍规避方法流程

在粒子群优化算法中,可行域判断是指要同时满足海事规则、无人艇最小回转直径及不与全局障碍物碰撞的约束。为了避免算法陷入局部最优,降低解算时间,在可行域的判断中设置海事规则判断最大次数;若判断次数大于设置的最大次数,则不对海事规则进行考虑。

5 仿真实验结果及分析

为了验证基于海事规则的水面无人艇动态障碍规避方法,采用在Visual C++平台上开发的水面无人艇危险避障算法仿真实验平台进行仿真实验分析。设立了如图7所示的避障环境,该避障环境包括了海事规则中正面相遇、交叉相遇、追越的3种情形,以及多障碍路径段的避障。

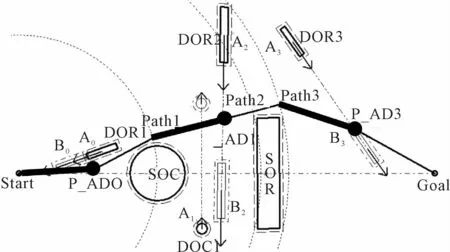
图7 仿真分析示意

在该仿真实验中,假定水面无人艇已经得到了全局最优路径节点Path1、Path2、Path3,“Start”为起始点,“Goal”为终止点,相距3 000 m;无人艇运行速度为40 kn,最大航速为50 kn。粒子群优化算法中惯性权重w采用线型递减策略,wmax= 0.95,wmin=0.2;c1=c2=2;m1=1,m2=70;设置粒子群迭代次数50,粒子数50。

该环境下包括一个全局静态圆形障碍物SOC,和一个全局静态矩形障碍物SOR。经过全局路径规划方法解算,得到全局规划路径节点见表1。包括1个动态圆形障碍物DOC1(见表2)和3个动态矩形障碍物DOR1、DOR2、DOR3(见表3)(分别选取上海外高桥制造的85 000 m3液化气船,18 000 TEU集装箱船和106 kDWT阿芙拉型原油船)。为了方便验证,将动态障碍物的起始位置均定为无人艇起始点的位置。动态障碍物起始时刻的位置用Ai表示,避障结束点时刻障碍物的位置用Bi表示,箭头方向为障碍物运动方向。

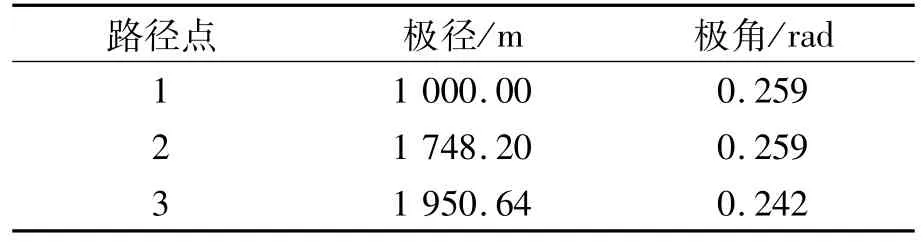
表1 全局规划路径节点

表2 圆形动态障碍物DOC参数

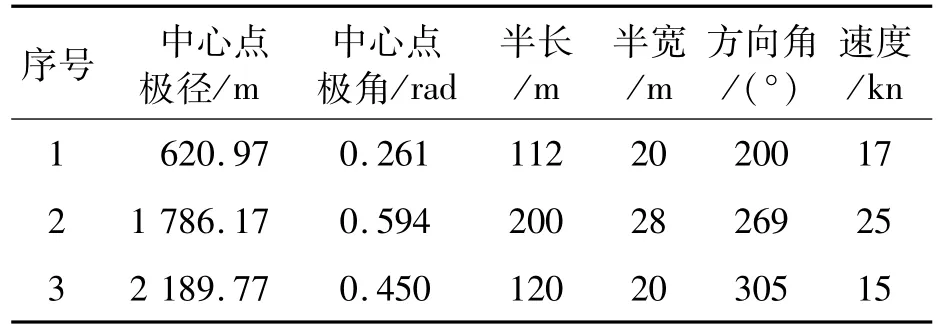
表3 矩形动态障碍物DOR参数

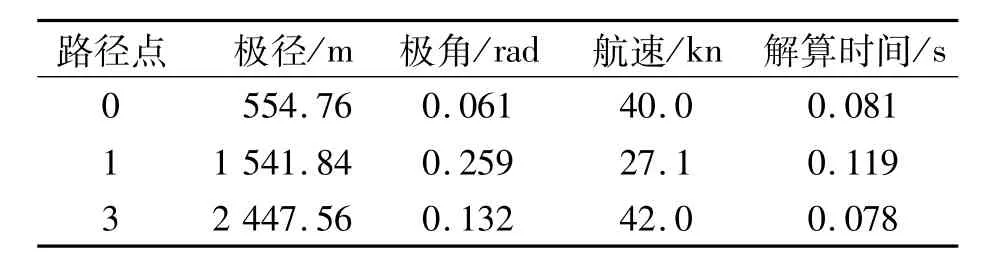
表4 动态障碍规避路径节点

无人艇在起始时刻时沿子目标点Path1航行时,探测到已知动态矩形障碍物DOR1,并与无人艇呈185.17°相向运行,即夹角在165°和195°之间,为海事规则中的正面相遇情形。若无人艇继续向前行进,会同障碍物相遇碰撞,所以需要无人艇做出相应的调整,从障碍物左舷即无人艇右转向通行。通过该算法解算,耗时0.081 s;得到的避障策略为向右舷转向11.34°,行进航速不变。避障结束点为P-AD0,其极坐标值见表4。图7中较粗的实线即为无人艇改变航速、航向进行避障的航线,成功避障后逐渐恢复航速至执行任务航速,朝向本段的全局子目标终点航行。

无人艇继续航行到Path1位置时,探测到动态圆形障碍物DOC1,和动态矩形障碍物DOR2,并分别从无人艇两侧驶来,角度分别为75.17°和254.17°;为海事规则中的交叉相遇情形,需要分别从两个障碍物的后方通过,即对DOC1而言为右侧通行,对DOR2而言为左侧通行。无人艇在Path1时刻进行避障,算法解算耗时0.119 s;得到的避障策略为航向不改变,航速从40 kn减少到27.1 kn行进。无人艇运行到避障结束点P-AD1后,就已成功完成了对障碍物DOC1和DOR2的规避,此时便逐渐加速到40 kn继续朝向本段的子目标点Path2航行。

无人艇运行到Path3位置时,探测到已知动态矩形障碍物DOR3,并与无人艇呈32.06°运行,即角度差在(0°,45°)之间,且无人艇航速(40 kn)大于障碍物速度(15 kn),为海事规则中的追越情形。此时需要无人艇做出相应的调整,从障碍物左舷即无人艇左转向通行。所以无人艇在Path3时刻通过该算法解算,耗时0.078 s;得到的避障策略为向左舷转向7.62°,航速增加到42.0 kn行进。无人艇运行到避障结束点P-AD3后,就已成功完成了对障碍物DOR3的规避。此时便逐渐恢复至执行任务航速40 kn,转向本段的子目标点即终点航行。

6 结束语

对障碍物进行包围体处理,使障碍物形状得到合理简化,减少了计算消耗,缩短了计算时间。且根据障碍物长宽比,采用圆形包围体或有向包围盒对障碍物进行简化;较好地解决了国内学者对无人艇会遇障碍物简化时,仅采用单一的圆形包围体处理而导致的损失大量可行区间、产生不合理避障策略的问题。

将国际海上避碰行为规则作为避障约束条件。通过仿真实验可得出,该算法不仅对单一障碍物避障适用,同时针对多障碍物规避问题,也可得到合理的避障策略。

将粒子群优化算法引入无人艇动态障碍规避中,很好地发挥了该算法在解决多目标优化问题中操作流程简单、参数简洁、收敛效果好的特点。通过仿真实验得出,避障解算时间在0.15 s之内;且根据避障情景可解算出仅改变航速、仅改变航向、同时改变航速和航向的3种可行策略。

仿真实验结果表明,该算法能够很好地完成对动态障碍物的规避,具有较强的环境适应能力、较快的解算速度、较好的避障效果,满足无人艇对障碍物规避的要求。然而由于部分障碍物存在运动不确定性,预测到的障碍物运动信息难免出现不准确的情况。针对这些障碍物若仅采用文中提出的算法,不能保障无人艇成功进行避障。所以下一步需要解决的问题是:无人艇根据视觉传感器或避障声呐等障碍识别系统实时探测并反馈障碍物当前位置信息,在文中提出算法的基础上,对阻碍无人艇航行的障碍物做出敏捷的应激反应式避障。

［1］YAN R,PANG S,S-UN H,et al.Development and missions of unmanned surface vehicle［J］.Journal ofMarine Science and Application,2010,9(4):451-457.

［2］BENJAMIN M R,CURCIO J A,LEONARD J J,et al. Navigation of unmanned marine vehicles in accordance with the rules of the road［C］∥Proceedings of the 2006 IEEE International Conference on Robotics and Automation.Orlando,Florida,USA,2006:3581-3587.

［3］庄佳园,苏玉民,廖煜雷,等.基于航海雷达的水面无人艇局部路径规划［J］.上海交通大学学报,2012,46 (9):1371-1375.

［4］卢艳爽.水面无人艇路径规划算法研究［D］.哈尔滨:哈尔滨工程大学,2010.

［5］马 闯,殷 波,马文帅.水上机器人三维实时避障算法研究［J］.微计算机信息,2009,25(3-2):235-237.

［6］CASALINO G,TURETTA A,SIMETTI E.A three-layered architecture for real time path planning and obstacle avoidance for surveillance USVs operating in harbour fields［C］∥OCEANS 2009-EUROPE.Bremen,German,2009:1-8.

［7］LEE S,KWON K,JOH J.A fuzzy logic for autonomous navigation ofmarine vehicles satisfying COLREG guidelines［J］.International Journal of Control Automation and Systems,2004,2(2):171-181.

［8］苏绍娟,王丽铮,王呈方.不确定性航线配船数学模型建模方法［J］.船海工程,2007,36(4):100-103.

［9］张丽平.粒子群优化算法的理论及实践［D］.杭州:浙江大学,2005.

A Dynamic Obstacle Avoidance Method of USV Based on COLREGS

DU Kai-juna,b,MAO Yun-shenga,b,XIANG Zu-quana,b,ZHOU Yong-qinga,b,SONG Li-feib,LIU Binb
(a.Key Laboratory of High Performance Ship Technology; b.School of Transportation,Wuhan University of Technology,Wuhan 430063,China)

To solve the problem for the unmanned surface vehicle(USV)avoiding the dynamic obstaclewhich is notmarked on an electronic chart,a dynamic obstacle avoidancemethod complies the international regulations for preventing collisions atsea (COLREGS)are presented.The dynamic obstacles are converted into an instantaneous static state related to USV in a motion moment,so as to compute the optimal speed and heading in real-time for the USV to avoid the obstacles by particle swarm optimization algorithm.Simulation experiments demonstrate that the dynamic obstacle avoidancemethod can calculate a reasonable avoidance strategy and accomplish the dynamic obstacle avoidance task effectively.

USV;dynamic obstacles;particle swarm optimization;path planning;maritime rule

10.3963/j.issn.1671-7953.2015.03.028

U675.85

A

1671-7953(2015)03-0119-06

2014-12-16

修回日期:2015-01-19

杜开君(1987-),男,硕士生

研究方向:船舶先进制造技术

E-m ail:dkjkls@126.com