GA-BP神经网络的钛合金微弧氧化膜层厚度预测模型的建立

牛宗伟*，李明哲

（山东理工大学机械工程学院，山东 淄博　255000）

GA-BP神经网络的钛合金微弧氧化膜层厚度预测模型的建立

牛宗伟*，李明哲

（山东理工大学机械工程学院，山东 淄博255000）

利用正交试验法获得的TC4钛合金微弧氧化实验数据建立了基于4-11-1（即4个输入神经元，11个隐含层节点，1个输出神经元）结构的BP神经网络预测膜层厚度的模型，并引入遗传算法（GA）对其权值和阈值进行优化。以微弧氧化工艺参数中的电流密度、脉冲频率、占空比和氧化时间作为网络的输入向量，氧化膜层厚度作为网络的输出向量，对比和分析了BP与GA-BP模型的预测结果。与BP网络模型相比，GA-BP网络模型稳定性能较好，并能高精度预测膜层的厚度，GA-BP网络模型预测值的平均误差为0.015，最大误差仅为0.036，而BP模型预测结果的平均误差为0.064，最大误差为0.099。

钛合金；微弧氧化；膜厚；预测；神经网络；遗传算法

First-author's address: School of Mechanical Engineering， Shandong University of Technology， Zibo 255000， China

微弧氧化又称微等离子体氧化，是在传统阳极氧化的基础上，利用弧光放电激活并增强工件表面发生的反应，从而在钛、镁、铝等阀金属及其合金表面形成优质陶瓷膜的方法［1-3］。它突破了普通阳极氧化的法拉第区，将电压引入到高压区域，在高电压作用下，工件表面发生微弧放电，材料产生熔融，熔融氧化物经电解液的冷淬最终形成陶瓷膜层［4-5］。该陶瓷膜层厚度大，硬度高，耐磨耐蚀性强，保护了基体金属，延长了其使用寿命［6-8］。膜厚是检验膜层质量的重要指标之一，通过选择合理的工艺参数来获得所需膜厚对微弧氧化工业生产有重要意义。然而微弧氧化反应影响因素较多，各因素耦合作用强，是高度非线性的复杂过程。人工神经网络的应用与发展为解决这类问题提供了可能。人工神经网络是一种仿照人脑结构及其功能构造出来的数学模型，具有较好的自学习、自适应及自组织功能［9-10］。它可学习样本数据，掌握输入、输出数据间的内在规律，非常适合处理微弧氧化这类复杂非线性系统问题。

本文利用正交试验法获得 TC4钛合金微弧氧化膜的厚度数据，建立了基于 BP神经网络（back propagation neural network）的微弧氧化工艺参数与膜厚之间的预测模型。针对BP神经网络在搜索权值与阈值时易收敛到局部而非全局最优解的问题，引入遗传算法（genetic algorithm，GA）对网络的权值与阈值进行优化，得到 GA-BP神经网络，并分析与比较了二者的预测结果［11-12］。

1　实验

将50 mm × 20 mm × 2 mm的TC4钛合金薄片分别用800#和2000#砂纸打磨，并用丙酮、酒精和去离子水除油、清洗，自然干燥后备用。采用日照润兴科技公司生产的微控全自动微弧氧化电源，该电源为单脉冲交流电源，电压0 ～ 600 V可调，电流密度0 ～ 100 A/dm2，微弧氧化电解液由16 g/L Na2SiO3、8 g/L （NaPO3）6以及2 g/L NaF组成，各原料均为化学纯。

采用L16（44）正交水平试验，研究了电流密度、脉冲频率、占空比和氧化时间对陶瓷膜层厚度的影响。用基于涡流原理的北京时代TT240涂层厚度测试仪测量膜厚，精度为0.01 μm，在基体正反两面的膜层各随机测量5个点的厚度，取平均值。正交试验结果见表1，其中带*的样本数据用来训练网络，其余作为预测样本。

表1　正交试验结果Table 1　Result of orthogonal test

2　GA-BP神经网络模型的建立

2. 1BP神经网络及样本数据处理

BP神经网络是以误差反向传播算法为训练算法的多层前向网络，包含正向及误差反向传播2个过程，是目前最常用的一种人工神经网络，其多以取值在［0,1］的 s形函数作为传递函数。网络训练前按式（1）对样本数据进行归一化处理［10］。

式中xn为样本数据，xmin与xmax分别代表数据中的最小值与最大值。

2. 2BP神经网络结构的确定

有研究证明，任何一个闭区间内的连续函数都可用3层的BP神经网络来逼近［9］。本文选用仅含1个隐含层的3层BP网络，其输入神经元数目为4，分别代表电流密度、脉冲频率、占空比和氧化时间；输出神经元数目为1，代表膜层厚度。隐含层节点数目对网络影响较大：若节点数目选取过少，网络对样本数据的学习能力较差，不能准确反映输入输出数据间的内在规律；节点选取过多则增加训练时间，降低了网络泛化能力，并可能导致过拟合现象发生［10］。一般采用经验公式（2）估算隐层节点数目：式中m为隐含层节点数，n为输入层节点数，l为输出层节点数，a为1 ～ 10之间的常数。经计算，隐层节点数的范围为4 ～ 12，对不同节点网络进行训练以确定最佳节点数。以表1中数据作为训练样本，训练次数为2 000次，收敛均方误差（MSE）设为10-5。不同节点数的网络性能如表2所示。

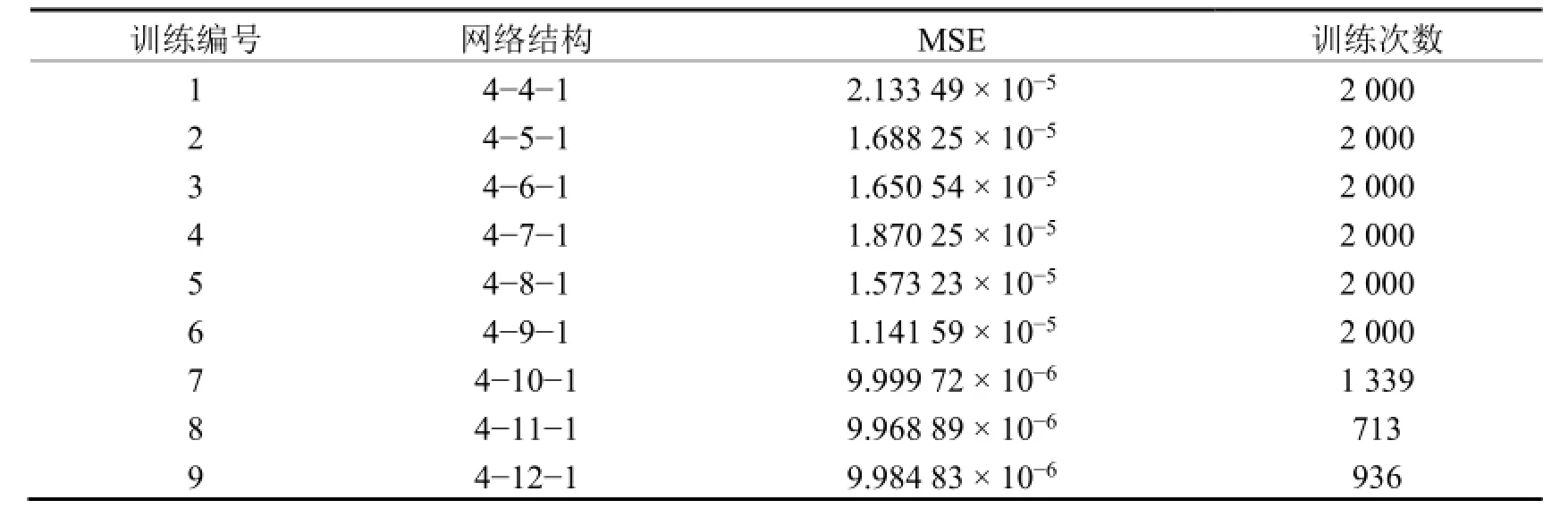
表2　不同隐层节点的BP神经网络训练误差Table 2　Training errors of BP neural network with different hidden layer nodes

由表2可见，节点数为10、11和12时，网络达到训练精度要求，且3个网络的精度差距不大。考虑到节点数为11时，网络训练次数最少，选择11作为隐含层节点数目，最终确定神经网络结构为4-11-1，其模型如图1所示。

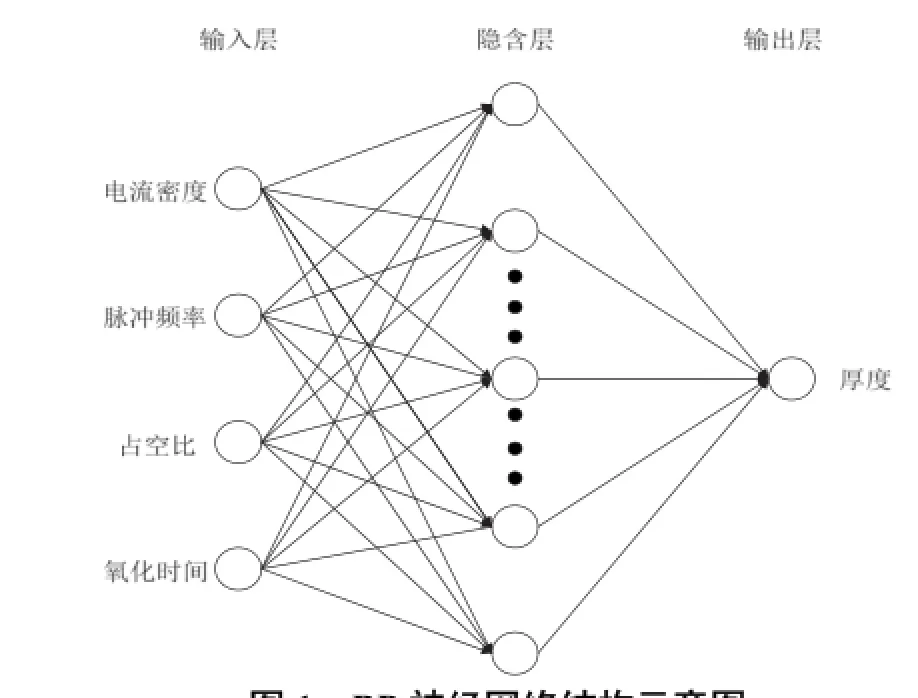
图1　BP神经网络结构示意图Figure 1　Schematic diagram of BP neural network

2. 3遗传算法优化过程

遗传算法是一种模拟生物进化论的自然选择和遗传学机理的生物进化过程的计算模型，通过模拟自然进化的过程搜寻全局最优解。遗传算法优化BP网络的过程包含初始化种群、适应度计算、个体的选择、交叉和变异操作。

网络模型中不同层神经元间通过权值与阈值连接，而同层神经元之间无连接。赋予网络输入与输出向量后，网络随机给出权值与阈值并参与计算得出网络输出值，为减小该网络输出值与输出向量的误差，网络会反向修正权值与阈值，然后以修正的权值与阈值再次进行计算，直到误差值达到设定标准。因权值与阈值由BP网络随机给出，所以常只能得到局部而非全局的最优解，从而影响了模型的预测精度。而遗传算法具有全局寻优的功能，故用它优化权值与阈值，就避免了权值与阈值的局部最优解［11-12］。

3　膜层预测及结果分析

3. 1 遗传算法优化BP网络

基于表1的正交试验数据，利用 MATLAB神经网络工具箱建立了 GA-BP神经网络模型，其训练函数是traingdx，该函数学习算法为Levenberg-Marquadt反传算法。参考资料［11-14］后分别选择tansig和logsig作为输入、输出层与隐含层的传递函数，收敛均方误差设为0.000 01，最大训练步数设为2 000次。GA优化过程中种群规模为20，迭代次数为100次，交叉与变异概率分别取0.5和0.09，进化过程中的平均适应度和最佳个体适应度曲线如图2所示。编制MATLAB程序对BP神经网络的权值和阈值进行优化，结果见表3，其下标表示不同层神经元的对应情况，头一位或两位数字表示隐层神经元（1 ～ 11），最后一位数字表示输入层或输出层神经元（输入层神经元数为1 ～ 4，输出层仅含1个神经元）。赋予网络优化过的权值和阈值后，对样本数据进行了仿真和预测。

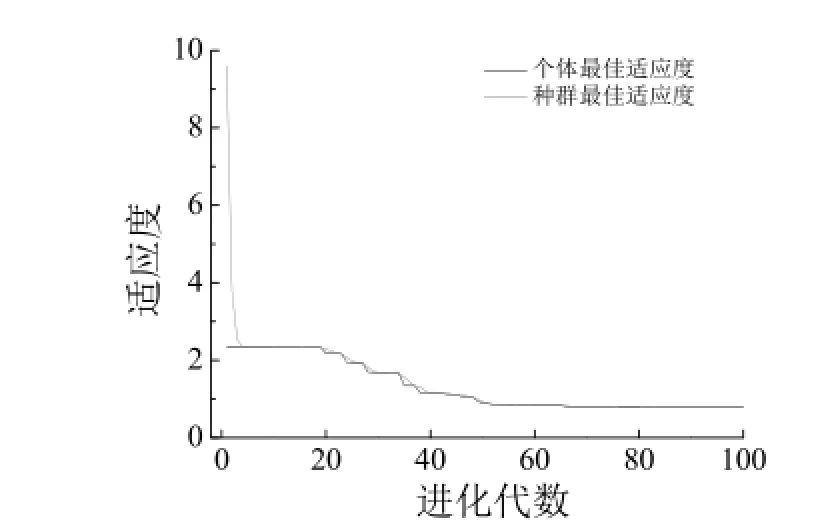
图2　适应度曲线图Figure 2　Fitness curve

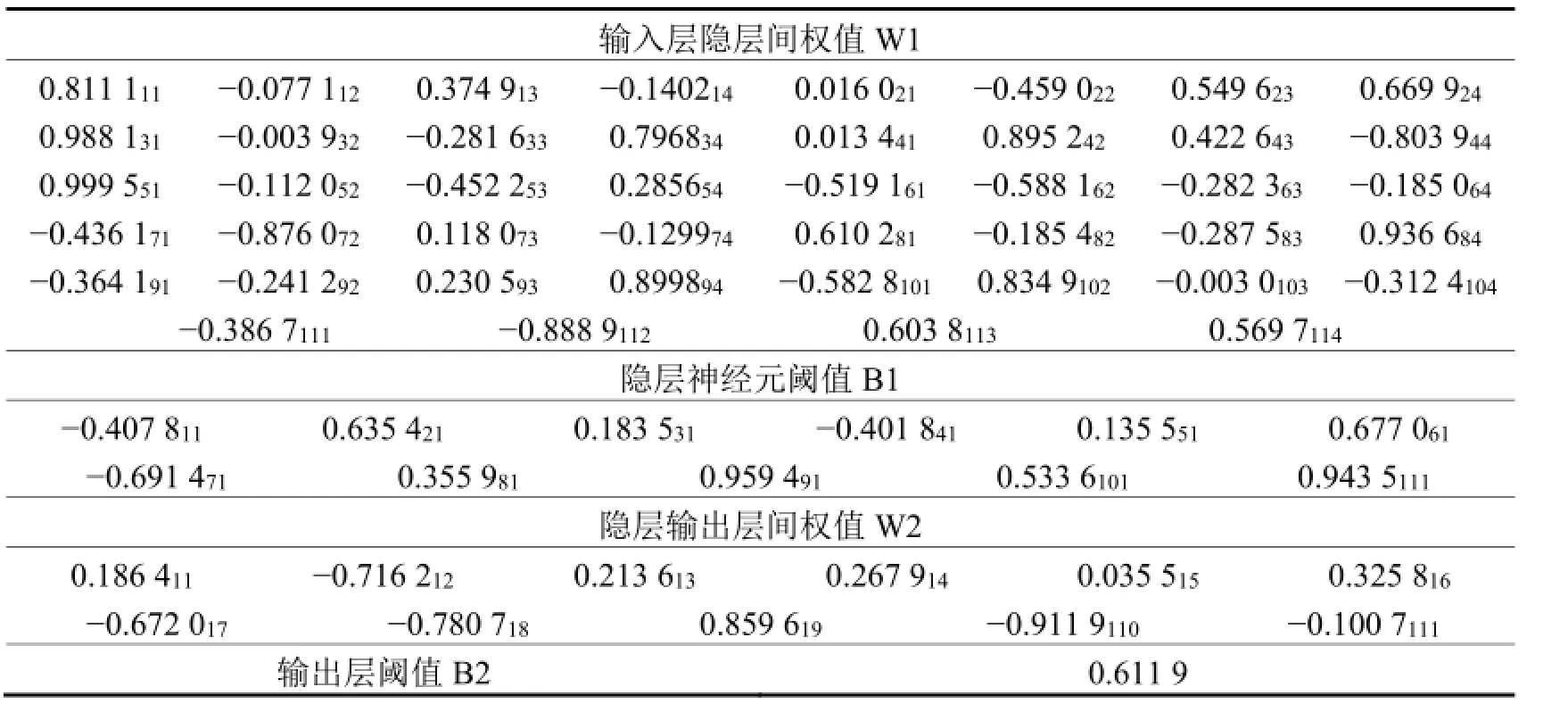
表3　优化后的BP模型权值和阈值Table 3　Weights and thresholds of optimized BP model

3. 2 仿真及预测结果分析

利用表1中带*号的样本数据训练优化后的网络，当训练精度达到要求后，学习过程结束。网络训练曲线如图3所示，当网络训练次数为389次时，达到精度要求。分别通过BP和GA-BP网络模型训练样本数据，仿真值与实验值的误差分布如图4所示。由图4可见，GA-BP网络的训练样本仿真误差浮动较为稳定，而BP网络的训练样本误差浮动较大。与BP网络模型相比，GA-BP网络模型预测性能更为稳定。

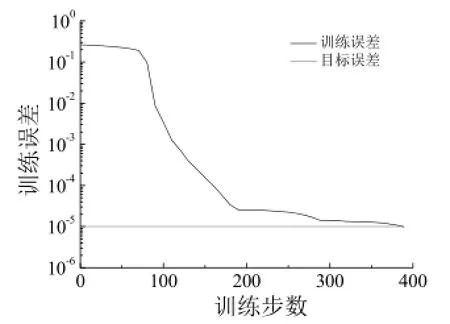
图3　GA-BP网络训练曲线Figure 3　Training curve for GA-BP network

图4　BP模型与GA-BP模型的仿真误差Figure 4　Simulation errors of BP and GA-BP models

选择表1中剩余的6组样本数据分别验证BP和GA-BP网络模型的预测性能，结果如表4所示。由表4可知GA-BP网络模型预测值的平均误差为0.015，最大误差仅为0.036，而BP模型预测结果的平均误差为0.064，最大误差为0.099，均大于GA-BP模型。可见GA-BP模型的预测精度更高。

BP与GA-BP模型的预测数据回归结果见图5和图6。图中Ce为膜厚实验值，Cp和Co分别为BP、GA-BP模型的预测厚度值。通过线性回归分析，获得了膜厚预测值与实验值的相关系数R，GA-BP与BP模型的R分别为0.999 3和0.996 8，相比之下，GA-BP模型的R更接近1，说明其有更高的预测精度和更好的泛化能力。

表4　BP与GA-BP神经网络预测结果Table 4　Prediction results of BP and GA-BP neural networks

图5　BP模型预测样本线性回归结果Figure 5　Linear regression result of predicted samples using BP model

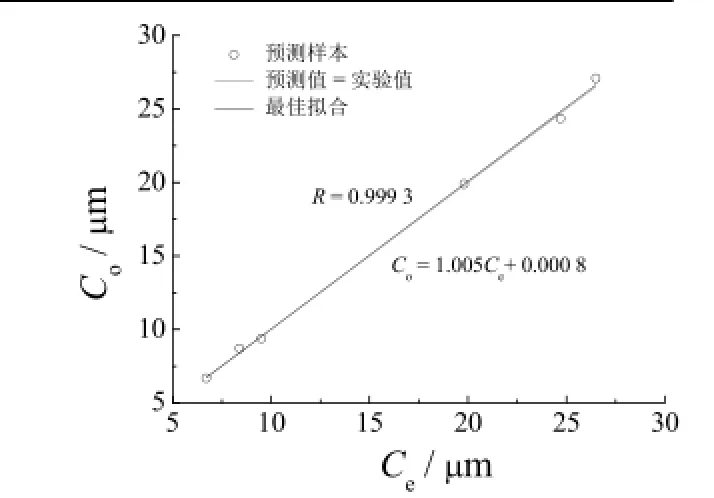
图6　GA-BP模型预测样本线性回归结果Figure 6　Linear regression result of predicted samples using GA-BP model

4　结论

选取微弧氧化过程中的工艺参数，建立了以电流密度、脉冲频率、占空比和氧化时间为输入，以膜层厚度为输出的BP网络结构，以遗传算法对BP网络权值与阈值进行优化，最终确立4-11-1的GA-BP膜层厚度预测模型。结果表明，与BP网络模型相比，GA-BP网络模型的稳定性较好，预测更为精确，可在一定程度上指导微弧氧化工艺参数的选定和优化，对实际生产具有一定的现实意义。

［1］ 王丽， 付文， 陈砺. 等离子体电解氧化技术及机理研究进展［J］. 电镀与涂饰， 2012， 31 （4）： 48-52.

［2］ YEROKHIN A L， NIE X， LEYLAND A， et al. Plasma electrolysis for surface engineering ［J］. Surface and Coatings Technology， 1999， 122 （2/3）： 73-93.

［3］ 王凤彪， 狄士春. 医用钛合金微弧氧化膜的制备及其生物相容性研究［J］. 电镀与涂饰， 2011， 30 （6）： 25-28.

［4］ 钟涛生， 蒋百灵， 李均明. 微弧氧化技术的特点、应用前景及其研究方向［J］. 电镀与涂饰， 2005， 24 （6）： 47-50.

［5］ 李克杰， 李全安. 合金微弧氧化技术研究及应用进展［J］. 稀有金属材料与工程， 2007， 36 （s3）： 199-203.

［6］ TSUNEKAWA S， AOKI Y， HABAZAKI H. Two-step plasma electrolytic oxidation of Ti-15V-3Al-3Cr-3Sn for wear-resistant and adhesive coating ［J］. Surface and Coatings Technology， 2011， 205 （19）： 4732-4740.

［7］ KHORASANIAN M， DEHGHAN A， SHARIAT M H， et al. Microstructure and wear resistance of oxide coatings on Ti-6Al-4V produced by plasma electrolytic oxidation in an inexpensive electrolyte ［J］. Surface and Coatings Technology， 2011， 206 （6）： 1495-1502.

［8］ CHEN M H， LI W B， SHEN M L， et al. Glass-ceramic coatings on titanium alloys for high temperature oxidation protection： Oxidation kinetics and microstructure ［J］. Corrosion Science， 2013， 74： 178-186.

［9］ TAN G P， WANG D F， LI Q. Vehicle interior sound quality prediction based on back propagation neural network ［J］. Procedia Environmental Sciences， 2011，11 （Part A）： 471-477.

［10］ BUFFA G， FRATINI L， MICARI F. Mechanical and microstructural properties prediction by artificial neural networks in FSW processes of dual phase titanium alloys ［J］. Journal of Manufacturing Processes， 2012， 14 （3）： 289-296.

［11］ 严浙平， 李滋， 陈涛， 等. 基于GA-BP神经网络的UUV航向容错控制［J］. 传感技术学报， 2013， 26 （9）： 1236-1242.

［12］ LIU K， GUO W Y， SHEN X L， et al. Research on the forecast model of electricity power industry loan based on GA-BP neural network ［J］. Energy Procedia，2012， 14： 1918-1924.

［13］ 田亮， 罗宇， 王阳. 基于遗传算法优化BP神经网络的TIG焊缝尺寸预测模型［J］. 上海交通大学学报， 2013， 47 （11）： 1690-1696， 1701.

［14］ 傅荟璇， 赵红. MATLAB神经网络应用设计［M］. 北京： 机械工业出版社， 2010： 83-91.

［ 编辑：杜娟娟 ］

Establishment of GA-BP neural network model for prediction of the thickness of micro-arc oxidation coating on titanium alloy

// NIU Zong-wei *， LI Ming-zhe

A model based on BP （back propagation） neural network with 4-11-1 （i.e. 4 input neurons， 11 hidden layer nodes，and 1 output neuron） structure for prediction of the thickness of micro-arc oxidation coating on TC4 titanium alloy was established using the data obtained by orthogonal test. The weights and thresholds were optimized by genetic algorithm （GA）. The prediction results of the BP and GA-BP models were analyzed and compared using current density， frequency， duty cycle，and oxidation time as input vectors and the thickness of oxidation coating as output vector. Compared to BP model， the GA-BP model possesses better stability and predicts the coating thickness with higher precision. The average and maximum prediction errors are 0.015 and 0.036 respectively for GA-BP model， and 0.064 and 0.099 respectively for BP model.

titanium alloy； micro-arc oxidation； film thickness； prediction； neural network； genetic algorithm

TG174； TP183

A

1004 - 227X （2015） 07 - 0381 - 05

2014-11-21

2015-01-28

国家自然科学基金（51005140）；山东省自然科学基金（ZR2010EQ037）；山东理工大学青年教师发展支持计划经费资助。

牛宗伟（1976-），男，山东日照人，博士，副教授，主要研究方向为先进制造技术。

作者联系方式：（E-mail） niuzongwei@sdut.edu.cn。