货物库存风险评价的两阶段fuzzy-AHP模型

李　慧，单而芳，孙广帅

（1.上海大学管理学院，上海200444；

2.青岛海尔日日顺物流有限公司，山东青岛266101）

货物库存风险评价的两阶段fuzzy-AHP模型

李慧1，单而芳1，孙广帅2

（1.上海大学管理学院，上海200444；

2.青岛海尔日日顺物流有限公司，山东青岛266101）

当前库存管理已经成为公司控制产品成本的一项主要指标.库存管理不仅能够保证货物的有效储存，同时也是保证公司的运作和生产效率的一种手段.通过对库存内部与外部各种影响因素进行深入分析，利用两阶段fuzzy-AHP模型，对货物库存的风险可能性及风险重要性进行评价；然后，将两种不确定性风险转化为可度量的量值，并通过比较不同仓库的库存风险系数，选择最优的存储方案，以及在最优存储方案下明确企业最应该关注的风险因素.

风险评价；库存管理；两阶段模糊层次分析法

我国目前的库存管理水平尚处在初级阶段，从库存的设备到库存的管理方法都存在很多缺陷，这些缺陷导致货物在存储过程中会产生较高的费用和损耗，因而对货物库存的风险评价就显得尤为重要.许多学者在库存管理方面进行了研究.刘晓峰等［1］运用Stackeberg博弈模型和机制设计理论，考虑了基于策略型消费者的最优动态定价和库存决策的问题.解琨等［2］通过对库存中安全库存量的分析，提出按服务水平确定安全库存量以降低企业库存的风险，并提出相应措施，但仅从库存量的角度考虑库存风险，并没有考虑其他影响因素.王凯兴等［3］主要研究了需求参数变化以及模糊需求条件下的库存风险及最优库存策略问题.李庆利［4］从风险分析的角度出发，研究了考虑缺货成本和积压风险情境下的随机需求问题，并运用概率和统计分析方法得出了企业最优订货数和最大收益.以上研究都是基于货物的库存量来进行的，通过将库存量控制在安全库存的范围内以降低企业库存的风险.这些研究使得库存风险过多集中在货物的库存数量上，忽略了库存管理中其他因素的影响.本工作将库存的风险因素归结为自然条件风险、人为条件风险、货物自身风险以及社会风险4个方面，并从这4个方面对库存的风险进行整体性研究，最后通过这4个最具代表性且相互独立的方面对库存进行综合性评价.

在风险评价的过程中，常用的方法是层次分析法（analytic hierarchy process，AHP）、风险矩阵法、神经网络法.利用AHP，刘娟等［5］进行了迁建项目HSE（健康（health）、安全（safety）和环境（environment）管理体系的简称）风险评价，得出了重要风险因素，但未能给出项目总风险度.熊杰等［6］运用AHP对航空项目风险因素进行了排序，并利用风险矩阵法给出了不同风险因素的风险度和项目总风险度，解决了层次分析法只能进行风险因素排序和方案选择的问题.艾时钟等［7］利用人工神经网络方法对库存的风险级别进行了预测.潘杰义等［8］利用风险矩阵对产学协作创新的风险进行了分析和评价.

模糊层次分析法（fuzzy-AHP）是近年来发展起来的一种更加符合实际的评价方法，它是在AHP的基础上通过引入了模糊数的概念，将AHP中专家对每个因素打出的具体分数变为分数范围，从而使得专家评测更具真实性和说服力.Chou等［9］利用fuzzy-AHP对科技人力资源的评估标准进行了研究；Rezaei等［10］利用fuzzy-AHP对多准则供应商分割的问题进行了研究；Ho等［11］利用fuzzy-AHP对物流外包的整合质量功能展开进行了研究.上述研究仅考虑了库存中的单一不确定性，忽略了实际问题中的其他不确定性.最近，Wang等［12］运用两阶段fuzzy-AHP模型研究了绿色供应链问题，并对多种具有不确定性的风险因素进行了重要性排序，进而得到了综合风险度.

两阶段fuzzy-AHP模型是在AHP的基础上延伸和发展而来的.在现实生活中，大部分的实际问题存在多种不确定性，而且多种不确定性之间也存在相互联系.以往的研究工作在运用fuzzy-AHP对风险进行评价时，往往仅考虑了问题的单一不确定性，而忽略了实际问题中其他的不确定性，因此在处理实际问题时不适用于多种不确定性同时存在的实际情况.本工作利用两阶段fuzzy-AHP模型将多种不确定性进行整合，并通过数学运算得到多种不确定性整合之后的数值，从而可以求得问题的最终风险指数.因此，运用两阶段fuzzy-AHP模型对实际问题进行研究更具有现实意义.

本工作主要是从库存风险的重要性和风险发生的可能性这两种不确定性，以及存在多种风险因素的情况下对库存货物进行风险性评价.通常由于评价的风险因素较多，并且大多数风险因素无法获取有效的数据信息，所以无法利用数据统计的方法进行有效分析.而利用两阶段fuzzy-AHP模型研究货物风险评价问题，只需要通过专家的评测给出一个分数范围，再将不确定的风险因素转化为定量的指标即可求出结果.这就使得问题的处理更加客观、简便、有效，同时也对库存管理中风险因素的重要性和风险发生的可能性这两种不确定性进行了较好的阐释.

1　模型描述

1.1三角模糊数的概念

三角模糊数（triangular-fuzzy number，TFN）的定义如下：假定F（R）为R上的全体模糊集，设M∈F（R），如果其隶属函数为µM：R→［0，1］，则有

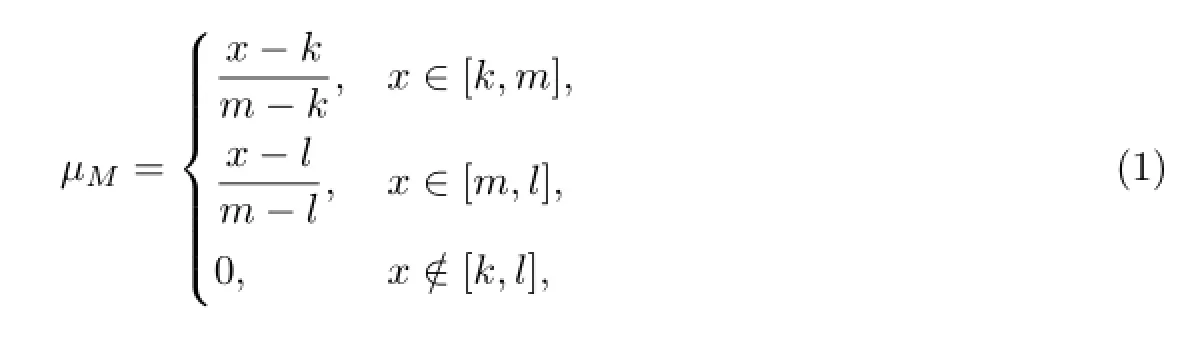
式中，M为三角模糊数，记为M（k，m，l）；k≤m≤l，k和l分别为M所支撑的下界和上界，l-k越大，表示模糊程度越大；m为M 的中值.特别地，µM有如下几种特殊情形［13］.

若k＜m=l，有

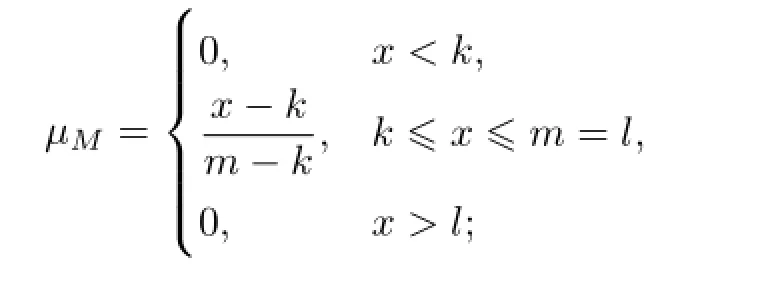
若k=m＜l，有

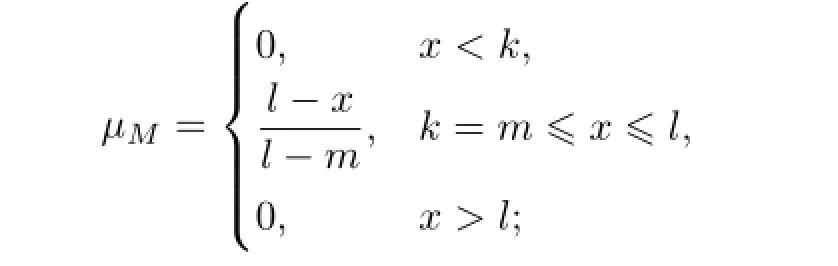
若k=m=l，有

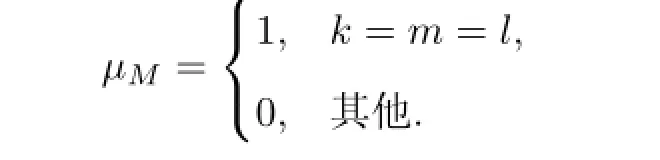
对于任意两个正三角模糊数M1（k1，m1，l1）和M2（k2，m2，l2），定义如下运算法则：

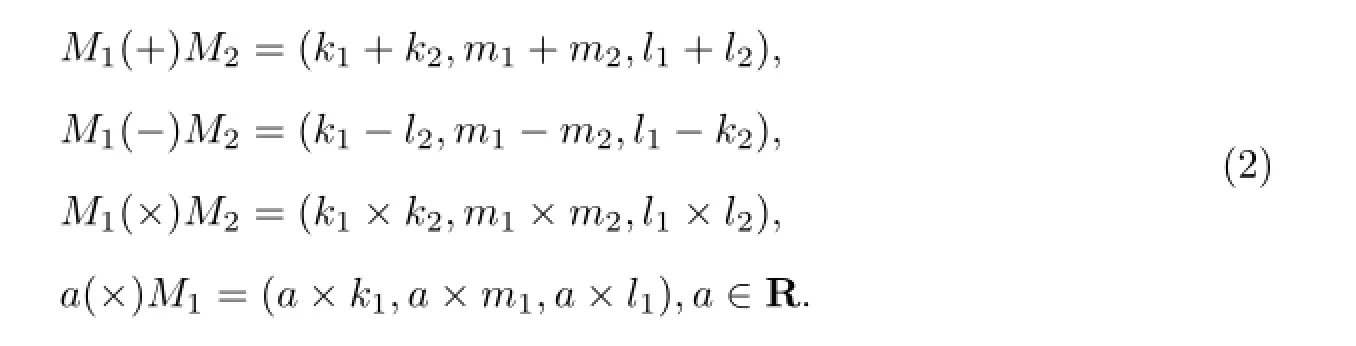
1.2利用三角模糊数构造风险评价标准

在现实生活中，由于信息的不确定和技术的缺乏，企业难以较准确地评价风险因素.另外，风险评价人员往往将风险因素按照风险的高、中、低来划分等级，这就导致不同风险因素之间差别不够明显.本工作利用三角模糊数将语言的不确定性评价转换为定量数据.Lee［14］曾提出了一个具有11个等级的定性评价标准，但是由于该标准过于复杂、实用性差，风险评价人员根据该标准难以对风险因素作出合理的评价.因此，一般情况下风险评价人员运用的是具有9个等级的评价标准［14］（见表1）.表1中构造了2个不确定性因素：库存风险的重要性和库存风险发生的可能性，这2个不确定性因素的三角模糊数决定了库存风险的大小和强度.将上述2个不确定性因素相乘建立风险评价等式，即

库存风险=库存风险重要性×库存风险发生的可能性.

表1　三角模糊数的风险评价标准Table 1 Risk evaluation criteria of triangular fuzzy numbers

由于三角模糊数具有模糊性，因此无法直接用于风险评价.考虑到三角模糊数的函数图像是对称三角形以及计算的简洁性，采用计算三角模糊数均值的重心点法［12］进行去模糊化处理，即

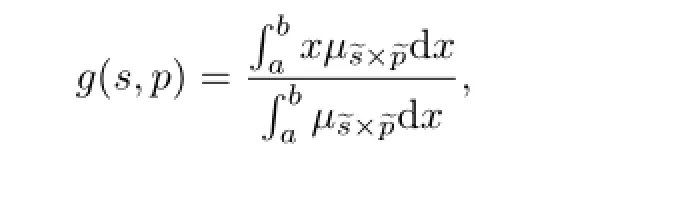
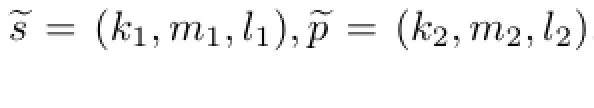
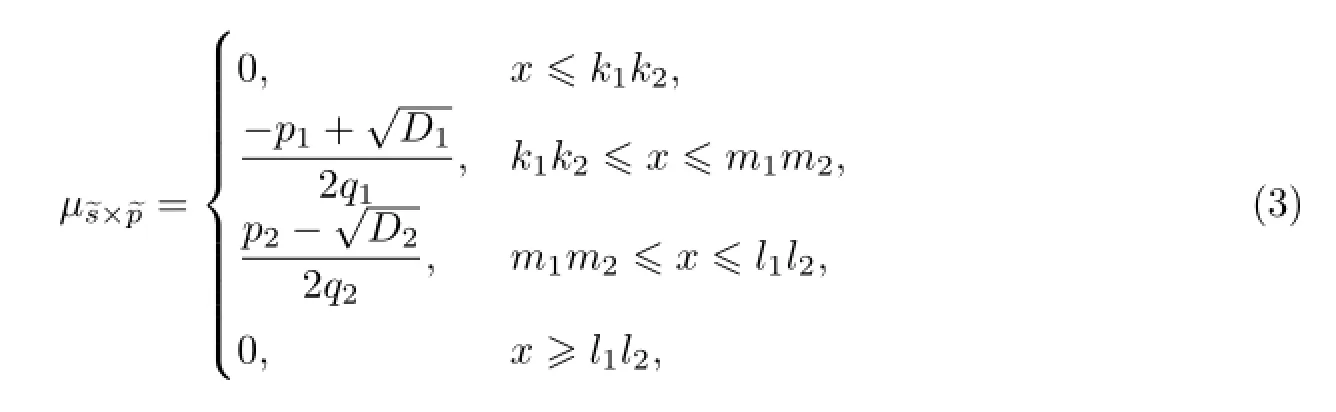
2　风险评价方法

2.1货物库存的风险因素

基于Ren［15］对库存风险因素的研究，本工作将从自然因素、货物本身因素、人为因素和社会因素以及这4类一级风险因素下的16个二级因素着手，对库存风险进行评价（见表2）.

表2　库存风险因素Table2Riskfactorsoftheinventory

2.2库存风险评价等级的构造

确定库存风险因素之后，为了避免主观判断引起的误差，提高指标评价的标准性，可以采用隶属度赋值的方法确定评语集V=（V1，V2，···，Vn）.本工作中，基于库存风险的评语集V=｛V1：（极低风险），V2：（较低风险），V3：（低风险），V4：（中等风险），V5：（高风险），V6：（较高风险），V7：（很高风险），V8：（极高风险）｝.

2.3建立正反互补矩阵，求出各因素权重

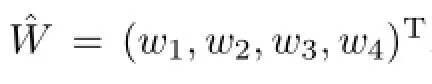
表3　三角模糊数评价表Table 3 Evaluation table of triangular fuzzy numbers

2.4评价矩阵的构造

首先，根据上述库存风险因素建立对应的三角模糊数评价表（见表3）；然后，根据重心公式求出各个等级的三角模糊数均值：V1=0.048，V2=0.14，V3=0.29，V4=0.43，V5=0.57，V6= 0.71，V7=0.86，V8=0.952.评价集V=｛V1，V2，···，V8｝中的各元素的数值与库存管理中的风险等级评价数值大小相对应.

2.5综合计算，得出结论

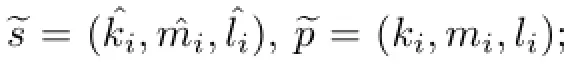
图1三角模糊数评级表Fig.1 Rating scale of triangular fuzzy numbers

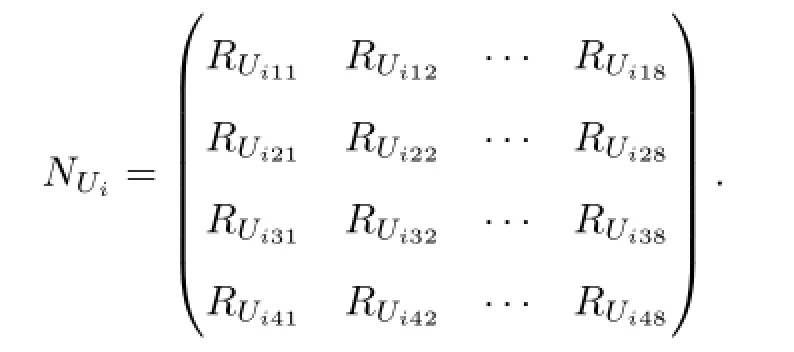
利用AHP，由专家对各二级风险因素进行测评，并构造出二级风险因素的正反互补矩阵；然后，求出各二级风险因素的相对权重，并进行一致性检验.各权重向量记为

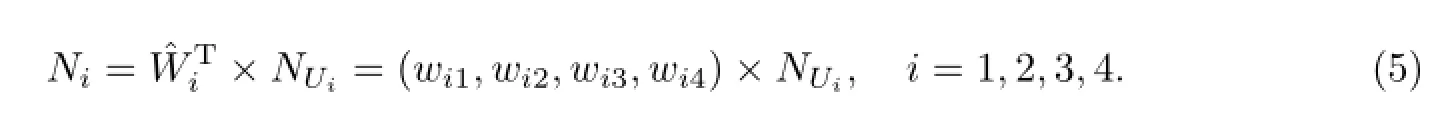
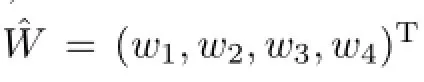
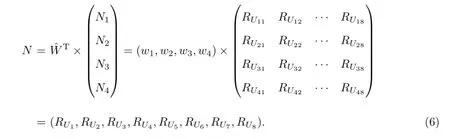
最后，由库存风险的总评价指标和根据重心公式求得的各等级的风险数值，可得综合风险指数（aggregative risk index，ARI）

ARI提供了一种定量方法来评判风险等级的大小，同时，也可以计算出不同仓库对于相同的库存因素的风险指数.根据风险评价等级可知，风险指数越低，货物在该仓库存储的风险就越低；风险指数越高，则代表货物在该仓库存储的风险就越高（见表4）.企业可接受的风险指数必须满足：ARI≤0.43.

表4　风险等级评价表Table 4 Evaluation table of risk level

3　案例分析

下面举例说明两阶段fuzzy-AHP模型在库存风险评价中的运用.具体方法是先根据专家的评价求出各二级风险因素的风险评价矩阵，并利用AHP构造二级正反互补矩阵，求出各风险因素的权重向量，利用二者相乘求出各一级风险评价矩阵；然后，构造一级正反互补矩阵得到一级风险因素的权重向量，将其与一级风险评价矩阵相乘求出综合风险矩阵；最后，将综合风险矩阵与各风险等级数值相乘得出ARI值，并将不同仓库的ARI值进行比较，确定最优库存方案.

仓库A和B各储存一批钢材，二者的风险因素评价如表5和6所示.

表5　仓库A的风险因素评价Table 5 Risk factors evaluation of warehouse A

表6　仓库B的风险因素评价Table 6 Risk factors evaluation of warehouse B

由表5先求出仓库A的综合风险指数.根据式（3），求出隶属度函数，再根据重心公式求得G11=0.065，G12=0.565，G13=0.545，G14=0.245.同时，可以求出U1的风险评价矩阵为

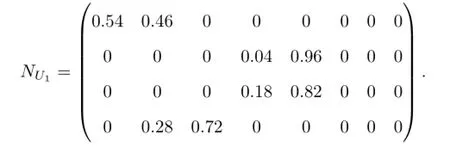
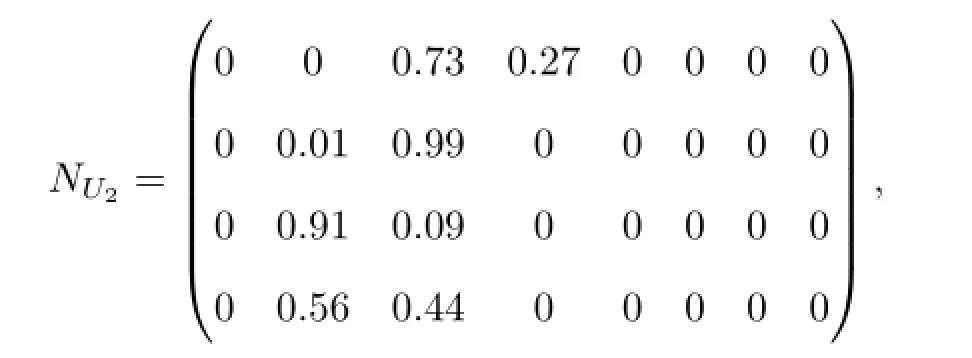
同理，对U2，U3和U4进行评测，可求得二级库存风险因素（见表7）.

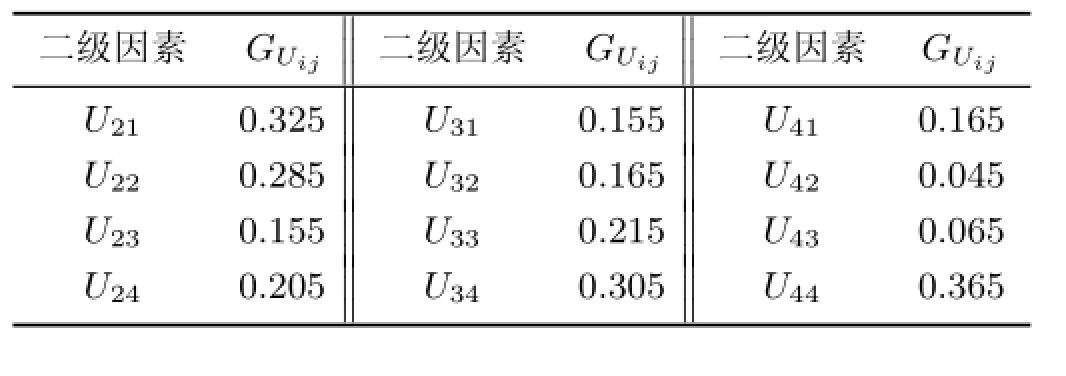
表7　二级风险因素GUij的值Table 7 Values of the second-echelon risk factors GUij

U2，U3和U4的风险评价矩阵分别为

3.1构造二级正反互补矩阵

根据专家对U1的各个二级风险因素的相对重要性进行评价，可以得到正反互补矩阵

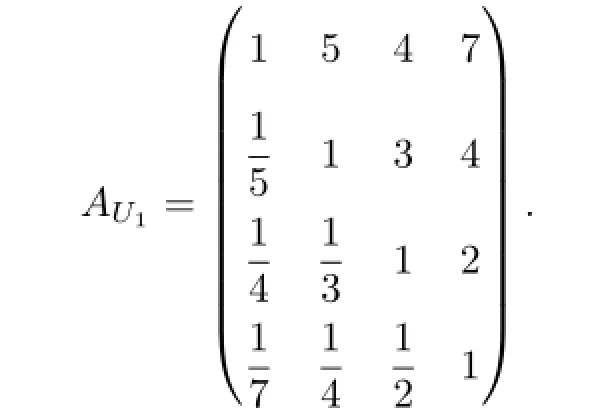
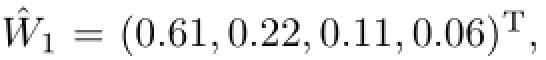
3.2Ui综合评价指标

根据式（5），可求得U1的综合评价指标为

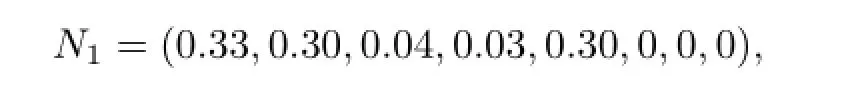
同理，可求得

3.3构造一级正反互补矩阵

根据专家对各个一级风险因素的相对重要性进行评价，可以得到正反互补矩阵

根据AHP的方根法，可以求出一级风险因素的相对权重指标，然后进行一致性检验.

3.4库存风险评价

根据式（6），可求得N=（0.19，0.43，0.22，0.04，0.12，0，0，0），再将库存风险的总评价指标Vn和根据重心公式求得的各等级的风险数值相乘，可求得

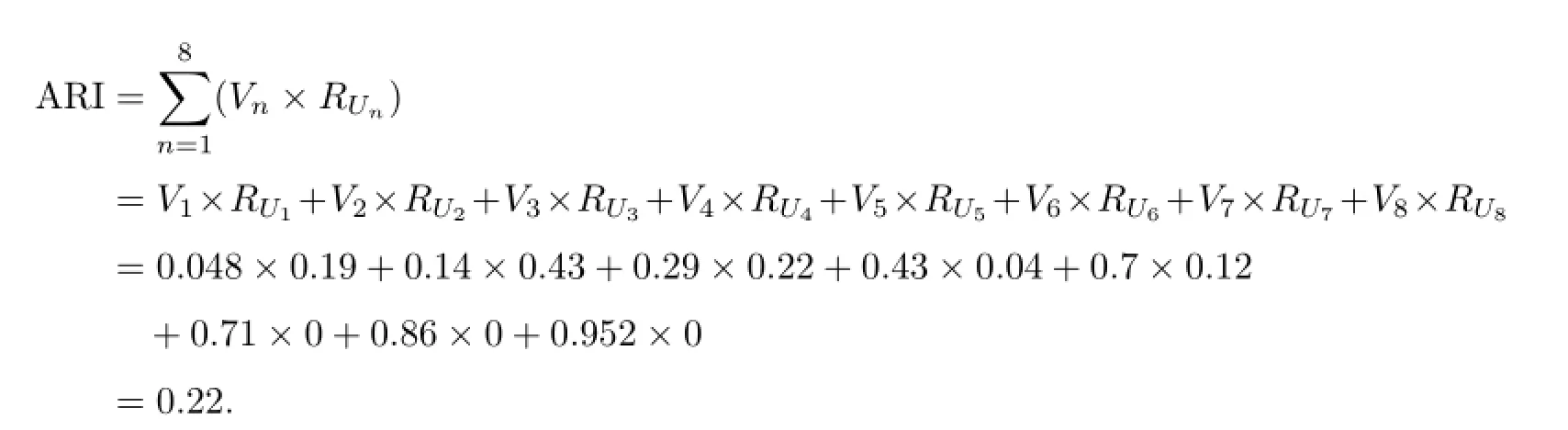
同理，可求得仓库B的综合风险指数为0.26.

3.5结果

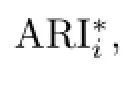
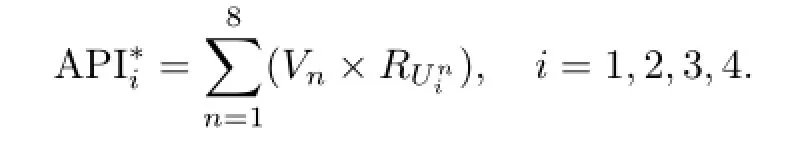
根据上式，可得到仓库A的4个一级风险因素的评价结果分别为0.10，0.21，0.22，0.15.可以看出，各风险因素的ARI值均小于中等风险等级0.43，其中人为条件的风险等级最大，介于低风险和中等风险之间.这说明，对于仓库A来说，人为条件因素对储存的货物影响最大，其次是货物自身风险、社会风险和自然条件风险.企业将货物储存在仓库A，应该特别关注人为条件及货物自身风险对货物的影响，并采取相应措施降低货物库存风险.

4　结束语

［1］刘晓峰，黄沛.基于策略型消费者的最优动态定价与库存决策［J］.管理科学学报，2009，12（5）：18-26.

［2］解琨，刘凯.降低企业库存风险问题研究［J］.中国安全科学学报，2002，12（5）：31-35.

［3］王凯兴，郭嗣琮.模糊需求下的库存风险及最优库存决策［J］.模糊系统与数学，2010，24（1）：98-102.

［4］李庆利.随机需求下的最优库存策略研究［J］.物流技术，2014，33（1）：259-261.

［5］刘娟，刘振奎.基于层次分析法的迁建项目HSE风险评价［J］.价值工程，2014，33（18）：65-66.

［6］熊杰，张善从.基于AHP和风险矩阵的航天研究项目风险评估［J］.科技进步与对策，2010，27（11）：124-126.

［7］艾时钟，杜荣.基于神经网络的备件库存风险级别预测［J］.中国管理科学，2008，16（S1）：430-433.

［8］潘杰义，赵飞.基于风险矩阵的产学协作创新风险分析与评估［J］.科技进步与对策，2012，29（22）：143-147.

［9］Chou Y C，Sun C C，Yen H Y.Evaluating the criteria for human resource for science and technology（HRST）based on an integrated fuzzy AHP and fuzzy DEMATEL approach［J］. Applied Soft Computing，2012，12（1）：64-71.

［10］Rezaei J，Ortt R.Multi-criteria supplier segmentation using a fuzzy preference relations based AHP［J］.European Journal of Operational Research，2012，225（1）：75-84.

［11］Ho W，He T，Lee C K M，et al.Strategic logistics outsourcing：an integrated QFD and fuzzy AHP approach［J］.Expert Systems with Applications，2012，39（12）：10841-10850.

［12］Wang X J，Chan H K，Yee R W Y，et al.A two-stage fuzzy-AHP model for risk assessment of implementing green initiatives in the fashion supply chain［J］.International Journal of Production Economics，2012，135（2）：595-606.

［13］冉静学.三角模糊数排序方法的研究［J］.中央民族大学学报：自然科学版，2011，20（4）：37-42.

［14］Lee H M.Applying fuzzy set theory to evaluate the rate of aggregative risk in software development［J］.Fuzzy Sets and Systems，1996，79：323-336.

［15］Ren S Y.Assessment on logistics warehouse fire risk based on analytic hierarchy process［J］. Procedia Engineering，2012，45：59-63.

Two-stage fuzzy-AHP model for risk assessment of inventory

LI Hui1，SHAN Er-fang1，SUN Guang-shuai2
（1.School of Management，Shanghai University，Shanghai 200444，China；2.Qingdao Haier Goodaymart Logistics Co.，Ltd.，Qingdao 266101，Shandong，China）

Inventory management is a major indicator for companies to control costs. Inventory management ensures goods to be stored efficently and keeps company stable operation.In this paper，various internal and external factors are analyzed.Using a twostage fuzzy-AHP method，the indices of two kinds of different possibility are calculated. The risk index of goods stored in different warehouse inventory are assessed to seek an optimal storage solution.The company should be clear which are the most influential risk factors under the optimal storage solution.

risk assessment；inventory management；two-stage fuzzy-AHP method

F 224.3

A

1007-2861（2015）06-0784-11

10.3969/j.issn.1007-2861.2015.01.005

2014-12-10

国家自然科学基金资助项目（11171207）

单而芳（1965—），男，教授，博士生导师，博士，研究方向为图论与网络优化、运筹与决策. E-mail：efshan@shu.edu.cn