远期运费协议与粮食期货市场的波动溢出关系

温　馨，丁　一，林国龙

（上海海事大学物流研究中心，上海 201306）

远期运费协议与粮食期货市场的波动溢出关系

温馨，丁一，林国龙

（上海海事大学物流研究中心，上海 201306）

从金融视角出发，探究远期运费协议和粮食期货市场之间的波动溢出关系.粮食作为世界三大干散货类型之一，具备相当成熟的期货交易市场，故选取远期运费协议（forward freight agreement，FFA）和巴拿马（Panamax）型船主要运载的粮食期货类型进行研究.首先，采取统计特征分析及协整检验对日收益序列进行分析；然后，通过建立广义自回归条件异方差（generalized autoregressive conditional heteroskedasticity，GARCH）模型，分析两个市场间的相关性并对比其波动性.结果表明，粮食期货市场在收益和波动性上均引导FFA市场的变化，论证了GARCH族模型检验波动溢出特征的有效性，并为干散货航运市场参与者和投资者提供理论参考.

远期运费协议；粮食期货；波动溢出性；自回归条件异方差模型

国际航运市场是国际贸易的派生需求，承担了全球90%以上的商品贸易量［1］.全球化和市场一体化的跨国贸易日趋成熟，交易成本的上升、信息的不对称性、供需的不协调及其他微观结构问题都会引起市场间的信息波动溢出和信息传递［2-3］.

国内外学者对于交叉市场间的信息传递关系、溢出性影响的研究大致可分为三类.第一类是在即期市场间通过供需作用彼此建立联系.例如：Yu等［4］研究了谷物现货市场与运价之间的关系，Haigh等［5］对驳船、海运运价和大豆价格之间的关系进行了实证研究.第二类是远期市场与相关即期市场间的信息流动关系.例如：Coppola［6］分析了远期市场与即期市场间的关系，Kavussanos［7］指出运价衍生品市场与即期市场之间存在联系.第三类是分析不同衍生品市场间收益和波动溢出性的关系.例如：Chng［8］讨论了天然气、元素钯和日本远期天然气市场之间的联系，Fung等［9］对美、中两国铝和铜的期货市场进行了对比，Kavussanos等［10］分析了运价衍生品和商品期货市场之间的关系，Ding等［11］对美股、债券和信用衍生品市场进行了研究，Trujillo-Barrera等［12］对美国原油、乙醇和玉米期货市场进行了分析，Beckmann等［13］论证了美国玉米、棉花和小麦期货市场的关系，Liu等［14］研究了中国的铜、铝、天然橡胶和大豆期货市场间的联系.

针对远期运费协议（forward freight agreement，FFA），已有的研究大多是将FFA与运价指数、即期市场建立联系.因此，本工作选择FFA与粮食期货市场为研究对象，并建立广义自回归条件异方差（generalized autoregressive conditional heteroskedasticity，GARCH）模型分析期货市场间的相关性及波动溢出关系.对粮食期货市场与FFA在价格波动上的溢出效应的研究，有助于较好地了解FFA价格形成的内在机理、市场信息的传导方式、市场运行效率与机制，更好地把握市场的波动性变化规律，为FFA参与者的决策提供理论支持与实践参考.

1　相关性及波动性模型

1.1Johansen协整检验

Engle等［15］指出：两个或多个非平稳时间序列的线性组合可能是平稳的，如果变量的相互偏离是短暂的，而长期又会达到某种均衡，这就是存在协整关系.Johansen等［16-17］建立了如下向量误差修正模型（vector error correction model，VECM），并提出了一种可以进行多变量协整检验的方法，该方法以向量自回归（vector autoregressive，VAR）模型为基础进行回归系数的检验：

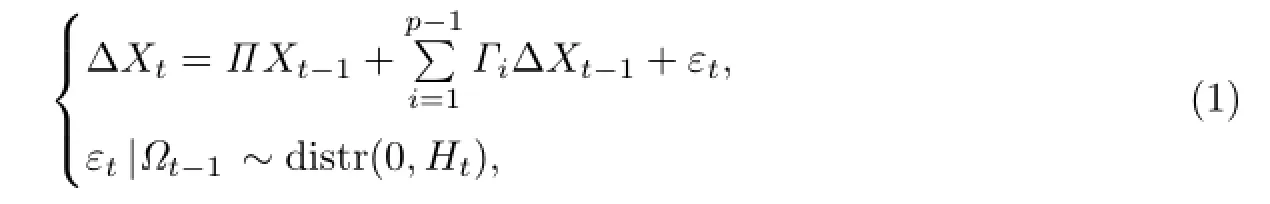
式中，Xt的各分量均为非平稳的I（1）向量，是一个确定的d维外生向量，用以表示常数项、时间趋势项等确定项；Γi为矩阵向量，εt为扰动向量，服从均值为0、随t变动的协方差矩阵为Ht的条件分布；Π=αβ＇，并要求β＇Xt-1的每行均为I（0）向量，即β的每一列所表示的Xt-1各分量的线性组合都是一种协整形式，所以Xt-1各分量之间协整向量的个数和形式取决于矩阵β.

1.2条件异方差模型

Bollerslev［18］提出的GARCH模型可以对市场间的相关性进行波动溢出性研究.与普通回归模型，如自回归条件异方差（autoregressive conditional heteroskedasticity，ARCH）等不同，GARCH模型还对误差的方差进一步处理，特别适用于对波动性的分析和预测.下面列出GARCH族中适合不同期货市场溢出效应的模型.

（1）GARCH（p，q）模型，其基本表达式为

式中，ω，α1，α2，···，αq和β1，β2，···，βp为待估参数，µt-i为前i期的时间序列，µt-j为前j期的时间序列.

式中，α反映前一期的波动情况，其大小反映了市场变化引起的序列波动性；β反映前一期的波动对序列影响的持续时间.虽然GARCH模型能够解决高阶ARCH模型的拟合问题，但不能反映时间序列波动的非对称效应（即杠杆效应）.

（2）GJR-GARCH模型.为了捕捉到正冲击和负冲击对序列波动的非对称性效应及波动和回报之间可能的相关关系，Glosten等［19］提出了GJR-GARCH模型：

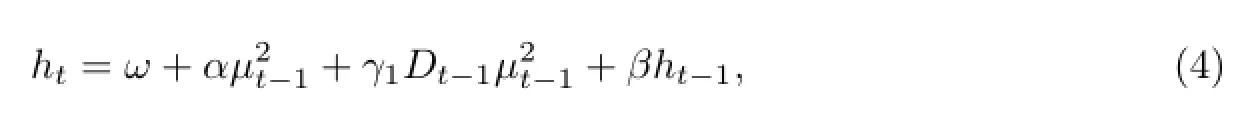
式中，当µt-1＜0时，Dt-1=1；当µt-1≥0时，Dt-1=0.条件方差ht非负的条件为ω＞0，2α+γ1＞0和β＞0.Engle等［20］利用信息反应曲线（news impact curve，NIC）分析比较了各种GARCH模型的杠杆效应，并认为GJR-GARCH模型较好地刻画了收益率的杠杆效应.

2　相关性及波动性模型实证分析

2.1数据的选取及处理

巴拿马（Panamax）型船FFA的发展历史最长，市场相对较为成熟.因此为保证交易数据的流动性和完整性，选取巴拿马型船两条航线P2A和PTC的FFA价格的日统计数据.巴拿马型船所承载粮食的比例占运载总量的43%，是所占份额最大的货载类型.选取4种粮食期货（玉米、小麦、大豆以及3种商品的平均价格）的日统计数据，数据来源于芝加哥商品交易所（Chicago mercantile exchange，CME）和分笔数据（Tick data）.调查区间为2006年5月—2009年10月，共868组日观测值.以P2A航线的FFA日数据为例，数据走势如图1所示.

图1　P2A航线的FFA日数据Fig.1 FFA daily return series of P2A

从图1可以看出：FFA日数据的波动幅度较大，且呈不规则的锯齿状；日数据值最高点（109 571）与最低点（6 500）相差较大；2008年（金融危机）前后，数据波动加剧，振幅较大.时间序列的分析主要是针对收益率序列进行的.收益率序列的计算方法为

由式（6）可以分别得到FFA和农产品期货的日收益率序列.

2.2统计特征分析

应用计量经济学软件包EViews 6对相关数据进行处理，可得到统计数据的样本均值、标准差、偏度、峰度、峰态和J-B（Jarque-Bera）统计量等.根据上述这些基本统计量，可以检验相关数据是否具有ARCH效应.基本统计量的特征分析如表1所示，表中A组为FFA价格序列，B组为粮食期货价格序列.

表1　统计特征分析Table 1 Analysis of statistical characteristic

分析表1中的数据，可以得到以下结论：①A组标准差均高于B组，且大致为B组的两倍，这说明FFA的波动更为剧烈；②除了玉米和小麦，其他组数据均具有明显的非对称性，或正向偏移，或负向偏移；③所有数据均高于峰态，且A组比B组呈现出更明显的尖峰厚尾特征；④J-B统计量的尾概率为0，这表明收益率序列拒绝正态分布的原假设；⑤ARCH检验表明，当滞后期为5时，收益率序列存在条件异方差性.

2.3平稳性检验

采用ADF（augmented Dickey-Fuller）检验验证统计数据是否平稳，即是否具有单位根.检验结果如表2所示.

表2　日收益率序列的ADF检验结果Table 2 ADF results of daily return series

由表2可以看出，5%显著性水平下的临界值为-2.86，而所有t统计量均小于该临界值，这表明样本数据的收益率序列不存在单位根，即日收益率序列为平稳序列.

2.4协整检验

对上述序列进行Johansen协整检验，但协整关系并未显现.分析原因可知，2007年12月开始了全球范围的金融危机，故2006年5月—2009年10月的样本数据出现突变.应用Gregory等［22］提出的基于结构突变的协整模型进行检验，具体结果如表3所示.

表3　协整检验结果Table 3 Cointegration test results

由表3可以看出：①通过Johansen协整检验，所有数据在5%和10%显著性水平上均不存在协整关系，这可能是因为金融危机的影响使得数据结构发生突变；②采用Gregory-Hansen结构突变协整检验［22］发现，在PTC-大豆期货、P2A-大豆期货和PTC-组合期货价格3组数据中存在结构突变的协整关系，并且这些数据序列发生突变的时间均在2007年12月前后，此时金融危机开始爆发，协整向量系数均显著服从t统计量；③玉米和小麦两种粮食期货与任何运价衍生品之间，均不存在上述两种协整关系，因此可以说FFA产品只与特定的商品期货之间存在长期均衡关系，而其他期货市场可能存在过度的投机行为，从而导致数据偏离了长期均衡状态.

2.5波动溢出性分析

由于收益率序列存在尖峰厚尾特征，故采用GARCH（p，q）模型进行估计.具体方法如下：①利用贝叶斯信息准则（Bayesian information criterion，BIC）确定阶数（p，q）；②采用极大似然估计法在t-分布下分别对模型的均值和方差进行参数估计；③利用Wald检验验证所得参数的有效性，并判断是否存在因果关系；④根据协整检验结果，将数据按有无协整关系分为两组建立模型.

对存在协整关系的3组数据建立VECM-GARCH模型，其中对PTC-大豆期货建立VECM-GJR-GARCH模型，对P2A-大豆期货和PTC-组合期货价格建立对称的VECMGARCH模型，具体公式如下：

式（7）～（10）中，ΔFFAt-i，ΔFUTt-i表示FFA和粮食期货价格的一阶对数差分；zt-1表示市场间的长期均衡关系；εi，t为随机误差项；aFFA，i，bFFA，i，aFUT，i和bFUT，i为短期关系系数.VECMGARCH模型的极大似然估计的结果如表4所示，其中A组为条件均值参数估计，B组为条件方差参数估计，C组为残差项检验.

分析表4中的数据，可以得到以下结论.对于条件均值参数估计：①qj均显著且异号，表示FFA与粮食期货呈反向协整关系，且长期均衡（如果市场上出现积极的信号预测，FFA价格将下降，而粮食期货价格将上扬，最终会达到均衡）；②在短期动态模型中bFFA，1显著，而aFUT，1，aFUT，2不显著，表示所有巴拿马型船所运载粮食的期货收益均对FFA收益起作用，该结果也同Wald检验的因果关系一致.也可以说，运价协议的需求来源于商品交易市场，从而导致运价市场的反应滞后于商品市场）.

对于条件方差参数估计：①滞后误差项ckk和滞后方差项bkk代表波动性，均显著；②在PTC-组合价格和PTC-大豆中，平方滞后项系数eci显著且为负数，表示先期数据对协整序列的条件方差有较强的预测能力；③在PTC-组合价格中，粮食期货价格对FFA的单向波动溢出性存在影响；④只有PTC-大豆没有表现出两个市场间的任何波动关系；⑤在P2A-大豆中FFA对粮食期货的波动溢出性存在影响；⑥相比较而言，粮食期货市场的信息性更强，因此在多数情况下，粮食期货市场会比FFA市场更早获知新信息.

对另外不存在协整关系的5组数据，采用VAR-GARCH模型进行极大似然参数估计，其中对PTC-玉米和P2A-组合价格建立VAR-GJR-GARCH模型，对P2A-玉米建立VAR-EGARCH模型，对PTC-小麦和P2A-小麦建立VAR-GARCH模型.具体公式如下：

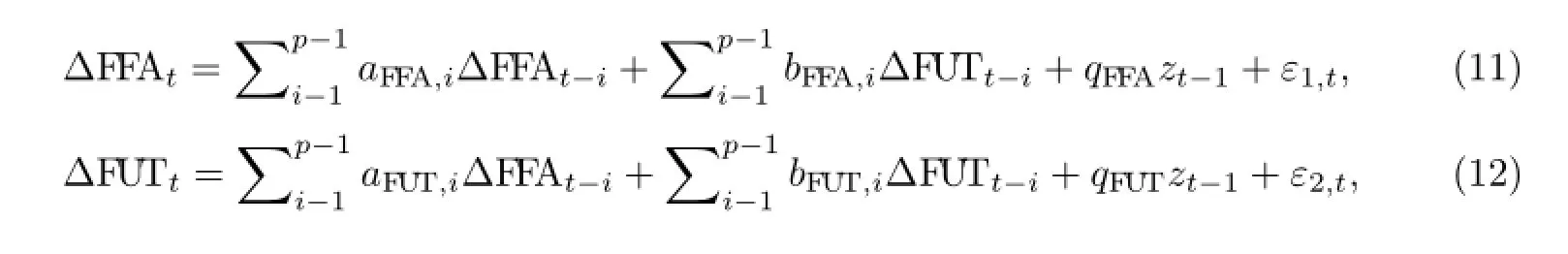
表4　VECM-GARCH模型的极大似然估计Table 4 Maximum-likelihood estimates of VECM-GARCH models

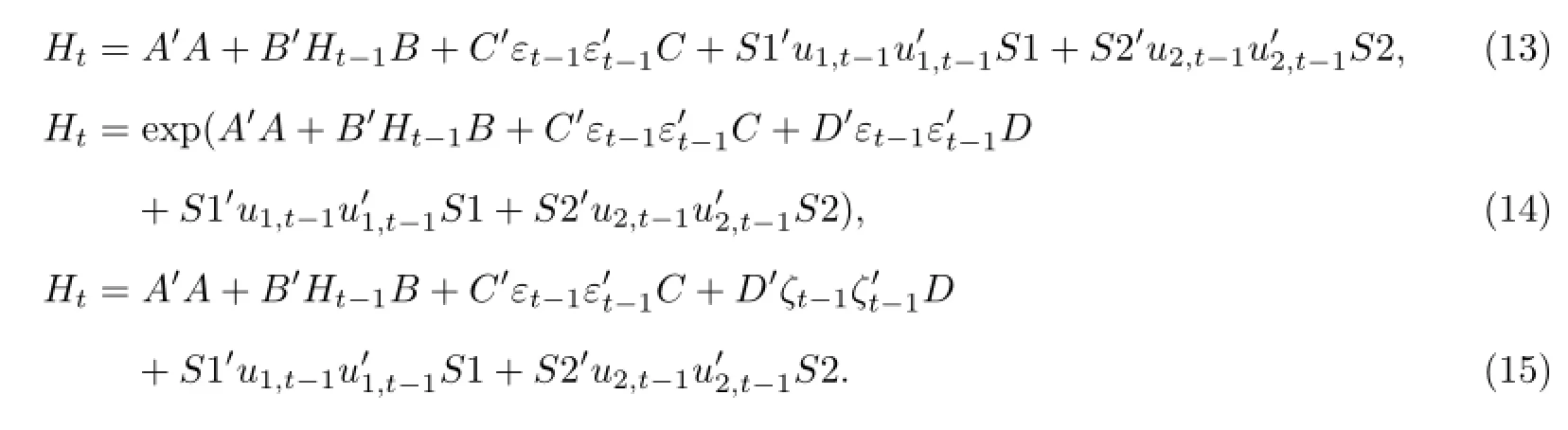
VAR-GARCH模型极大似然估计的部分结果如表5所示.

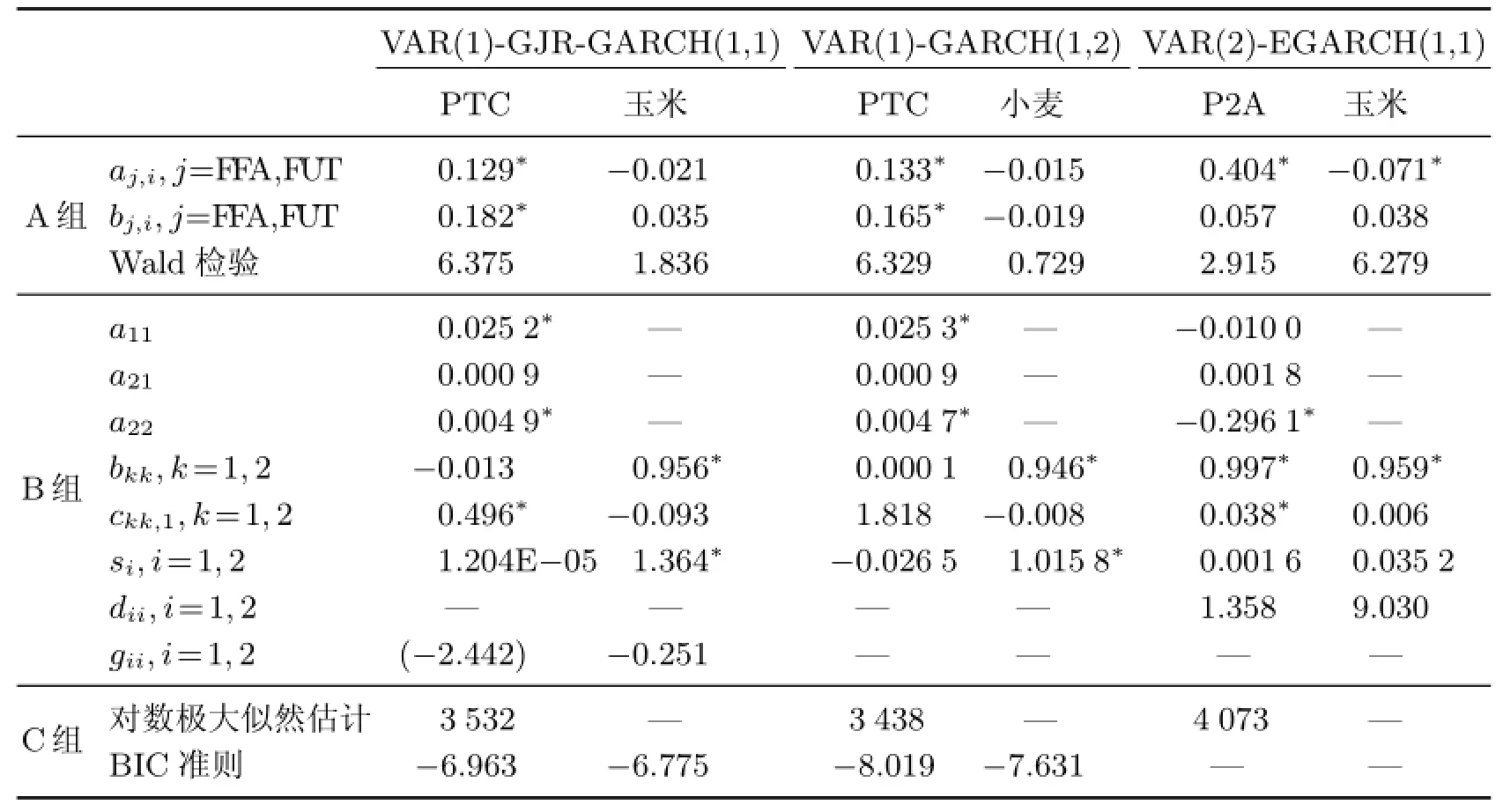
表5　VAR-GARCH模型的极大似然估计Table 5 Maximum-likelihood estimates of VAR-GARCH models

由表5可以得出以下结论.对于条件均值参数估计：①bFFA，1，bFFA，2显著，而aFUT，1，aFUT，2不显著，表示信息首先会出现在粮食期货市场上，所以无论是否存在长期协整关系，粮食期货市场都有较强的信息性；②P2A-玉米与其他组有所不同，FFA的价格发现功能要先于粮食期货市场，因此按实际市场交易情况来看，玉米的实体交易较其他商品类型而言，会更多地影响干散货船市场.

对于条件方差参数估计：①由ckk和bkk可以看出，PTC-玉米、PTC-小麦中粮食期货对FFA的波动溢出性存在影响；②在P2A-小麦、P2A-组合价格中存在双向因果关系，且由si可以看出，粮食期货对FFA的影响更强；③仅在P2A-玉米中未发现相互波动关系，因此，巴拿马型船可从粮食期货市场成功获取新信息.

综上分析可知，粮食期货市场在收益和波动性上均引导FFA市场.粮食期货收益与FFA收益呈单向溢出关系；在波动性上，粮食期货市场与期租平均航线PTC呈单向关系，与P2A存在双向关系.

市场受到信息冲击时，由于基本面的影响作用，当其中一个市场的价格发生变化时，其他市场也可能随之发生变化.因此，市场投资者往往可以根据某些市场价格来判别其他市场的价格变化并进行决策行为，从而增加了市场间的风险传递.对以上实证结果可作如下解释：一方面表明市场关联性增强，因为航运市场是国际化程度较高的市场，与其他市场（如粮食等）、子市场之间都存在关联性，并且在全球金融危机的大环境下，市场之间的关联性不断增强；另一方面，与FFA市场相比，商品期货市场更为成熟，因此在价格变化时可以传递更为有效的信息.商品期货市场的流动性较高，日均交易量约为FFA市场的3倍，市场摩擦和错误定价也相对较少，交易成本更低.Chordia等［23］指出，高效运作的市场交易成本较低，进而引导交易量增多，从而使得市场的有效性更强.FFA主要是航运业用来规避风险、进行套期保值的工具，市场参与度较低，远不如主流商品期货市场.FFA市场始于1992年，而小麦和谷物期货交易开始于1877年，大豆开始于1936年，所以商品期货市场体系更稳定.商品期货市场的价格基本取决于供需状况，而FFA市场取决于场外交易市场（over the counter，OTC）的供需，实际的出价、交易额、成交量等信息并未完全公开.

3　结束语

对巴拿马型船FFA市场和粮食期货市场之间的波动溢出关系进行实证分析，研究结果表明，在大多数情况下，收益和波动方面的新信息在传递到FFA市场之前，首先会出现在粮食期货市场，证明了运价衍生品和粮食期货市场之间存在波动溢出效应.对于小麦、玉米和大豆这些重要的粮食期货种类，可以通过借鉴这些市场的波动特征，更好地掌握FFA市场变化趋势，为运价市场交易和运转提供引导性方向，从而使得FFA市场进一步良性发展.对参与航运业的船东、贸易商、投资基金等企业和机构来讲，所得结果有助于更深入地了解FFA市场的波动性、波动溢出效应，把握市场的变化规律，从而可以直接有效地作出交易、投资、租赁和风险管理等市场决策.

虽然FFA市场与粮食期货市场存在波动溢出关系，但研究范畴略显不足.干散货运输市场包括Capesize，Panamax和Supramax三种细分市场，且运载的主要货物除了粮食，还有铁矿石和煤炭.因此，今后的研究方向可以扩展到铁矿石、煤炭等市场，并与不同干散货船型建立联系.通过实证分析，可以进一步丰富交叉期货市场间的相关理论，更深入地了解FFA市场的波动性和波动溢出效应以及投资者的行为，从而可以直接有效地进行风险管理.

［1］George R.Ninety percent of everything：inside shipping，the invisible industry that puts clothes on your back，gas in your car，and food on your plate［M］.London：Henry Holt&Company，2013：128-146.

［2］Wahab M，Lashgari M.Price dynamics and error correction in stock index and stock index futures markets：a cointegration approach［J］.Futures Market，1993，13（7）：711-742.

［3］Fleming J，Ostdiek B，Whaley R E.Trading costs and the relative rates of price discovery in stock，futures and options markets［J］.Futures Market，1996，16（3）：353-387.

［4］Yu T H，Bessler D A，Fuller S W.Price dynamics in US grain and freight markets［J］. Canadian Journal of Agricultural Economics，2007，55（3）：381-397.

［5］Haigh M S，Bryant H L.The effect of barge and ocean freight price volatility in international grain markets［J］.Agricultural Economics，2001，25（1）：41-58.

［6］Coppola A.Forecasting oil price movements：exploiting the information in the futures market［J］.Futures Market，2008，28（1）：34-56.

［7］Kavussanos M G.Business risk measurement and management in the cargo carrying sector of the shipping industry［M］.London：Lloyds of London Press，2010：709-743.

［8］Chng M T.Economic linkages across commodity futures：hedging and trading implications［J］. Journal of Banking and Finance，2009，33（5）：958-970.

［9］Fung H G，Liu Q F，Tse Y.The information flow and market efficiency between the U.S.and Chinese aluminum and copper futures markets［J］.Futures Markets，2010，30（12）：1192-1209.

［10］Kavussanos M，Visvikis I，Dimitrakopoulos D.Information linkages between Panamax freight derivatives and commodity derivatives markets［J］.Maritime Economics and Logistics，2010，12：91-110.

［11］Ding L，Pu X L.Market linkage and information spillover：evidence from precrisis，crisis，and recovery periods［J］.Econ Business，2012，64（2）：145-159.

［12］Trujillo-Barrera A，Mallory M，Garcia P.Volatility spillovers in US crude oil，ethanol，and corn futures markets［J］.Journal of Agricultural and Resource Economics，2012，37（2）：247-262.

［13］Beckmann J，Czudaj R.Volatility transmission in agricultural futures markets［J］.Economic Modelling，2014，36：541-546.

［14］Liu Q F，Wong I，An Y B，et al.Asymmetric information and volatility forecasting in commodity futures markets［J］.Pacific-Basin Finance Journal，2014，26：79-97.

［15］Engle R F，Granger C W J.Co-integration and error correction：representation，estimation，and testing［J］.Econometrica，1987，55（2）：251-276.

［16］Johansen S.Statistical analysis of cointegration vectors［J］.Journal of Economic Dynamics and Control，1988，72（2/3）：231-254.

［17］Johansen S，Juselius K.Maximum likelihood estimation and inference on cointegration-with applications to the demand for money［J］.Oxford Bulletin of Economics and Statistics，1990，52（2）：169-210.

［18］Bollerslev T.Generalized autoregressive conditional heteroskedasticity［J］.Journal of Econometrics，1986，31：307-327.

［19］Glosten L R，Jaganathan R，Runkle D E.On the relation between the expected value and the volatility of nominal excess return on stock［J］.Journal of Finance，1992，46：1779-1801.

［20］Engle R F，Ng V K.Measuring and testing the impact of news on volatility［J］.The Journal of Finance，1993，48（5）：1749-1778.

［21］Nelson D B.Conditional heteroskedasticity in asset returns：a new approach［J］.Econometrica，1991，59（2）：347-370.

［22］Gregory A W，Hansen B E.Residual-based tests for cointegration in models with regime shifts［J］.Journal of Econometrics，1996，70：99-126.

［23］Chordia T，Roll R，Subrahmanyam A.Recent trends in trading activity and market quality［J］.Journal of Financial Economics，2011，101（2）：243-263.

Volatility spillover effect between forward freight agreement and grain futures market

WEN Xin，DING Yi，LIN Guo-long
（Logistics Research Center，Shanghai Maritime University，Shanghai 201306，China）

From the financial point of view，this paper investigates volatility spillovers between forward freight agreement（FFA）and grain futures market.As one of the three major dry bulk cargoes in the world，grain has a mature futures market.FFA and main grain futures transported by Panamax are studied.First，statistical characteristics and co-integration relation of daily return series are analyzed and inspected.A generalized autoregressive conditional heteroskedasticity（GARCH）model is then constructed to analyze correlation and volatility spillover.The results indicate that the grain futures market leads to the changes of FFA market with respect to return and volatility.Thus，this paper demonstrates effectiveness of GARCH-class model to test volatility spillover，providing a theoretical basis for shipping operators.

forward freight agreement（FFA）；grain futures；volatility spillover；generalized autoregressive conditional heteroskedasticity（GARCH）model

F 550

A

1007-2861（2015）06-0774-10

10.3969/j.issn.1007-2861.2015.01.006

2014-08-09

国家高技术研究发展计划（863计划）资助项目（2013A2041106）；国家自然科学基金资助项目（71101088，71301101）；教育部博士点基金资助项目（20113121120002）

温馨（1989—），女，硕士研究生，研究方向为国际航运、航运金融.E-mail：985651039@qq.com