基于准则的大展弦比飞翼气动设计
2015-10-19甘文彪周洲许晓平
甘文彪,周洲,许晓平
(1.北京航空航天大学 无人驾驶飞行器设计研究所,北京100191;2.西北工业大学 航空学院,西安710072)
现代高空无人机(UAV)设计对气动和隐身性能的要求越来越高,为了在一定的隐身条件下取得更高的气动性能,典型的先进高空无人机(如RQ170、RQ180等)均采用大展弦比飞翼布局.大展弦比飞翼无人机翼身高度融合,需要严格满足装载和隐身要求,具有特殊的气动性能,其气动设计主要受3个方面的影响:①机身布置以及机身对展向流动的影响;②机翼典型截面翼型的流动特征;③机翼翼面参数变化以及翼尖效应.随飞行速度的变化,大展弦比飞翼无人机的展向流动特征和二维截面翼型的特征将发生显著的变化,这将深刻地影响其升阻和力矩性能.
为改进飞翼的气动性能,很多作者针对飞翼开展了相关研究分析[1-7].Wood和 Bauer对100年来飞翼布局飞机的研究进行了回顾[8],Grellmann介绍了 B2 飞机的气动设计[9],Liebeck针对亚声速翼身融合的飞翼布局飞机进行了设计研究[10],Mialon等针对飞翼构型开展了气动优化设计[11],Qin等也对翼身融合(BWB)的飞翼布局飞机进行了气动性能研究[12],Leifsson等对分布式BWB构型开展了多学科优化设计[13],胡添元开展了飞翼布局飞机总体多学科设计优化研究[14],鲍君波等开展了飞翼布局气动方案优选和试验验证[15],这些以及其他与飞翼相关的研究工作都能够为飞翼无人机的气动设计提供借鉴,但大多侧重于小展弦比飞翼布局气动分析研究,对大展弦比飞翼的流动特征和气动优化设计体现的少,而本文将针对大展弦比飞翼无人机来开展气动设计和流动特征分析.
1 设计方法
1.1 设计准则
从设计实际和工程实用出发,针对大展弦比飞翼无人机气动构型开展设计,其研究主体是:为提高设计效率和避免多学科设计的复杂性,结合设计的先验知识,以最优气动性能为目标,在装载、强度和隐身约束下来确定飞翼全机外形.
事实上,理解分析大展弦比飞翼布局形式,可以对其构型设计提炼出如下准则:①由于全机基本构型暂不考虑推进系统,因此对进排气系统的隐身和流动要求,不需要细化;②在设计时需要满足总体设计对翼面积的要求,设计过程将在总体设想的初始构型上展开;③由于机身任务载荷和翼面装载的需要,各部件必须满足重量学科对厚度和弯度的基本要求,且必须光滑过渡(特别是机身);④为满足隐身设计的要求,翼面的前后缘必须保证边缘绕射集中的要求(满足平行布置);⑤为了满足最基本的结构强度要求,各部件的弦长和面积必须控制在一定范围(特别是翼面转折处的弦长和翼梢的弦长);⑥由于翼身融合和全翼面设计的需要,各部件需要耦合调配来设计,也就是说设计时必须同时考虑各部件影响,设计从三维入手来展开,并分析流动特征,进而精细化检验设计的可行性,这是最重要的准则.
依据准则,可细化得到几个设计的基本约束条件:①仅给出推进系统的装载位置和大小,暂不研究推进系统的流动特征;②全机翼面积大小基本不变;③机身必须具有适当的曲面造型,将采用多曲线来辅助控制;④翼面前后缘必须满足一定的平行条件;⑤各部件具有一定的弦长和面积约束范围.结合约束条件可确定大展弦比飞翼无人机的初始构型,示意如图1所示.

图1 飞翼无人机初始构型Fig.1 Initial configuration of flying wing UAV
1.2 设计框架
基于设计准则,结合变可信度的气动数值模拟方法、代理模型和优化算法来构建优化设计分析体系[16],优化设计方法框架如图2所示.变可信度的气动数值模拟方法包括:①基于改进SST(Menter’s Shear-stress Transport)湍流模型的雷诺平均Navier-Stokes方程数值模拟方法(简称改进SST方法);②基于γ-Reθt转捩模型的雷诺平均Navier-Stokes方程数值模拟方法(简称γ-Reθt方法).在设计过程中,采用多轮次更新优化设计的策略,基于改进SST方法通过优化设计得到推荐构型;接着应用γ-Reθt方法对优化结果进行了更细致地分析,进而确定设计结果的流动特征和可行性.
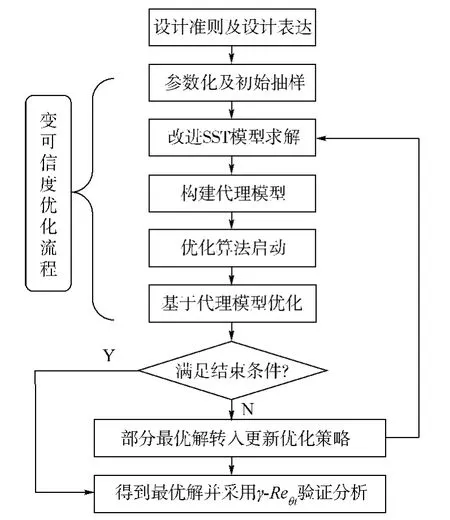
图2 优化设计方法框架Fig.2 Optimal design method framework
1.3 CFD求解方法
采用有限体积法求解可压缩流动雷诺平均Navier-Stokes方程组.时间离散采用近似因子(AF)方法,无黏项空间离散使用上风Roe格式,黏性项采用中心差分.
湍流模型采用改进SST湍流模型和γ-Reθt转捩模型(分别对应改进SST方法和γ-Reθt方法).SST湍流模型的改进包括涡量产生项和分离修正(如式(1)和式(2),其中f5为分离相关系数);γ-Reθt转捩模型的 Flength的经验关系如式(3),Reθt采用Keerati给定的函数来确定,详细公式见文献[16].湍流模型求解采用非耦合平均流动方程的隐式方法,模型对流项采用二阶离散.详细参数和验证见文献[16].

2 设计模型
2.1 设计表达及参数化方法
飞翼无人机基本构型通过参数化方法来表达设计问题,具体方法是:①基于隐身和装载要求,确定机身对称截面、翼身过渡截面,各采用10个变量的Hicks-Henne型函数方法来参数化,共20个变量;②机身通过上下各5条NURBS曲线来确定,并按照装载要求作出强约束,设计变量共有20个;③基于流动特征和翼面积限制,确定前缘后掠角、后缘前掠角和5个典型截面弦长(即对称面、翼身过渡截面、kink、翼梢和翼尖的弦长),共7个变量,由于限定面积,展长的约束通过弦长变量范围来间接给定;④确定kink和翼梢的特征截面翼型,采用10个变量的Hicks-Henne型函数方法来参数化,共20个变量;⑤确定翼身过渡截面、kink和翼梢3个特征截面之间的多个定位截面,这些定位截面仅用来辅助生成NURBS曲面,其曲率变化由3个特征截面来决定,因此不增加设计变量;⑥确定第③和第④点的设计变量为主设计(即主层次)变量,这些设计变量包括面参数和特征截面参数共27个,为弱约束变量;⑦确定第①和第②点的设计变量为次要设计(即次层次)变量,包括机身对称截面、翼身过渡截面和机身上下曲面的参数化变量,共40个变量.
2.2 设计过程的实现
为减小设计过程的计算量,采用分层设计的思路:①针对次要设计变量,关注翼身流动的展向变化,依据设计准则中的装载要求,对设计变量作出强约束,设计变量空间较小,为提高设计效率,采用均匀设计结合灵敏度分析来修形设计[16],进而确定机身对称截面、翼身过渡截面和机身上下曲面;②针对主设计变量采用多目标免疫遗传算法[16]和径向基函数(RBF)来进行优化迭代,得到最终的优化构型.这里将针对主设计变量,阐明设计过程的实现和设计结果的分析.
在设计过程中,机身截面的NURBS曲线将通过5个点来控制,其中首末2个点和中点坐标确定,中间2个点的法向坐标(相对壁面来说)为设计变量,NURBS曲线详细形式见文献[16].
截面翼型的Hicks-Henne型函数方法参数化.a1~a5为加权参数,n和m分别为扰动幅度和宽度函数,取值为a1~a4对应的n为3,m为0.1、0.3、0.5、0.7,a5对应的 n 为 1,m 为0.9.
优化时通过程序来修改设计变量,并应用NURBS曲面来使其转化为数字曲面的特征控制量,进而针对数字NURBS曲面采用无限插值技术来更新实体模型.得到更新实体模型后,基于无限插值技术,通过程序来进行网格变形重构,从而实现网格的自动生成,图3给出了优化时自动生成的飞翼无人机网格,显然网格质量较高.

图3 飞翼构型自动生成的网格Fig.3 Automatically generated grid of flying wing
优化过程包括多次CFD求解、代理模型重构、优化迭代.主层次设计时经过5轮次的更新优化设计,每轮次以包含200个个体的抗体群进化30代,进化结束后向样本库增加5个样本点,共针对217个全机外形进行了CFD计算,以RBF作为代理模型,并随每一轮次逐步更新代理模型;针对最终的优化设计结果开展了32次验证计算.
3 优化设计结果及分析
飞翼基本构型优化设计指标是:巡航状态Ma=0.65、CL=0.5时有尽可能高的升阻比,纵向力矩静稳定度不小于5%.具体设计目标为:Ma=0.65,α =2.5°的升阻比 k1;Ma=0.7,α =2.5°的升阻比k2.具体约束条件为:Ma=0.65,α=2.5°时的力矩系数有dCM/dCL≤-5%.
图4给出了多轮更新优化补加的样本点与优化解的验证结果(图中Add-points表示补加样本点,Add-path表示补加样本前沿,Opt-points表示优化解).图中标示出了5轮优化补加样本点的前沿,补加样本点的前沿逐步趋向于优化解,体现了多轮优化不同于单轮优化的设计效果.
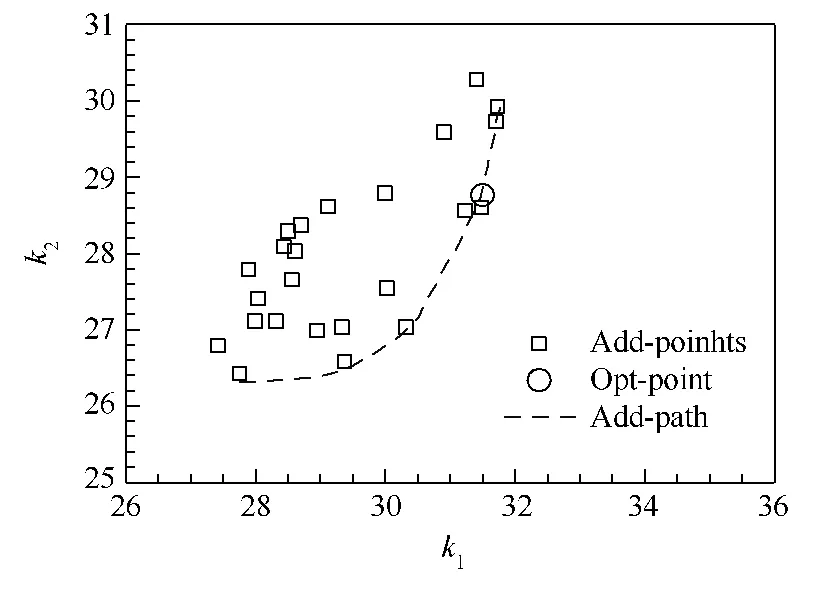
图4 补加样本外形与设计外形验证结果Fig.4 Verification result of appearance with added samples and design shapes
3.1 巡航速度下的验证结果
图5给出了原始和优化构型Ma=0.65巡航状态时验证计算结果的对比,显然优化构型的失速更和缓;升阻比有显著提高(以改进SST方法计算为例,由27.8增大到31.7,即约增大14%,相应的γ-Reθt计算则为37.4);设计构型的力矩静稳定性略有下降,但仍能满足设计要求的力矩约束.整体来看,相比改进SST(即图中的SST,图中Ori表示原始设计,Opt表示优化设计)方法计算,γ-Reθt方法计算的气动性能更高,这是因为:一般情况下,γ-Reθt方法能较好预测转捩[16],对摩擦阻力的计算精度更高.

图5 飞翼原始与设计构型气动性能(Ma=0.65)Fig.5 Aerodynamic performance of original and design configuration of flying wing(Ma=0.65)
图6是巡航状态Ma=0.65,α=2.5°时的飞翼设计构型表面压强分布与极限流线图.由图可知,全机上表面未出现明显的激波,在kink位置两侧流动出现了弱压缩波流动特征;机身的极限流线向对称面偏折,这一现象是由后缘压力分布所决定的;这可能对以后喷管设计带来影响;依照准则为提高设计效率,这里暂不考虑推进系统.

图6 飞翼设计构型压强分布及极限流线(Ma=0.65,α =2.5°)Fig.6 Pressure distribution and limit streamlines of design configuration of flying wing(Ma=0.65,α =2.5°)
为说明流动的湍流特征,图7给出了巡航状态Ma=0.65,α=2.5°时截面的湍流涡黏性图,图中标示了上下表面转捩的大致位置,图中机身曲面有明显的隆起,符合设计准则对装载的要求.由对称面向外,上表面转捩位置先逐渐前移,再后移,最后处于与前缘平行的固定相对弦长位置.转捩变化情况反映出:翼身过渡截面与kink位置截面之间存在展向流动调整区,这个调整区显著影响流动的展向发展.随攻角增大该调整区的流动可能发生分离,对气动性能有严重影响.

图7 飞翼设计构型涡黏性分布(Ma=0.65,α=2.5°)Fig.7 Eddy viscosity distribution of design configuration of flying wing(Ma=0.65,α =2.5°)

图8 飞翼设计构型翼尖流线(Ma=0.65,α=2.5°)Fig.8 Streamlines of flying wing wingtip of flying wing design configuration(Ma=0.65,α =2.5°)
为反映空间流线特征,图8给出了巡航状态Ma=0.65,α=2.5°时飞翼设计构型翼尖流场.由图可知,翼尖涡较弱,反映了优化构型对翼尖的处理是比较成功的.事实上,翼尖弦长较长,翼尖曲面变化迅速,这符合设计准则对弦长的限定(弦长在较长的合理范围).
随攻角增大的流动特征对全机的稳定性影响较大,图9和图10分别给出了Ma=0.65,α=4°时的飞翼设计构型表面和截面的压强分布.由图9可知,在机身上表面流动未出现明显的激波和压缩波,在机翼上表面由里向外流动出现了压缩波和激波.由图10可知,对称截面(η/b=0,η为截面到对称截面的距离,b为展长)存在弱压缩波,kink位置(η/b=25%)存在弱压缩波,η/b=60%存在弱激波,随展向向外,在η/b=95%形成了完整的激波,且激波强度较大.

图9 飞翼设计构型压强分布(Ma=0.65,α=4°)Fig.9 Pressure distribution of flying wing design configuration(Ma=0.65,α =4°)

图10 飞翼设计构型各截面压强分布(Ma=0.65,α=4°)Fig.10 Section pressure distribution of flying wing design configuration(Ma=0.65,α =4°)
图11为Ma=0.65,α=6°时飞翼的典型压强和摩擦阻力系数分布.由压强分布可知,机身与机翼过渡区的流动由两道激波逐渐汇聚成一道激波,机翼上表面有明显的激波.由摩擦阻力系数分布可知,在激波后流动发生了转捩.机翼上表面激波对压强分布的显著影响,使得机翼上的升力主要集中在激波前,这将导致全机力矩静稳定性的下降.
综合图9~图11可知,全机各部件进行了耦合调配(特别是从机身沿展向向外的曲面变化),符合设计准则;宏观上,当攻角较大时,将导致流动沿展向从多道弱压缩波或弱激波向激波的转化.

图11 压强和摩擦阻力系数分布(Ma=0.65,α=6°)Fig.11 Pressure and friction coefficients distribution(Ma=0.65,α =6°)
3.2 不同速度下的验证结果
为进一步探讨设计构型的气动特征,这里针对Ma=0.6和Ma=0.7时的非设计状态开展计算分析.计算采用方法.图 12 是不同速度下飞翼设计构型气动性能对比.随速度增大,全机的失速提前,最大升阻比下降,在小攻角时力矩静稳定性增大,大攻角时力矩静稳定性显著减小;这都反映出:速度增大,激波对全机的影响增大.
图13给出了不同速度典型攻角下飞翼设计构型的表面压强分布.由压强分布可知,Ma=0.6时流动并未出现激波和压缩波,而在Ma=0.7时在机身和kink位置附近流动出现了激波,如图中标示;显然复杂的展向流动使机身到kink位置的临界马赫数降低.

图12 不同马赫数下飞翼设计构型气动性能对比Fig.12 Aerodynamic performance contract of design flying wing configuration at different Mach

图13 不同速度下飞翼设计构型的压强系数分布(α=2.5°)Fig.13 Pressure distribution coefficient of flying wing design configuration at different speed(α =2.5°)
图14为不同速度下α=6°时设计构型的压强分布.在Ma=0.6时,kink位置以外流动存在明显的激波.在Ma=0.7时,全机上表面的压强分布说明流动由对称面向外都存在激波;由极限流线可知,在kink位置的内侧近旁流动发生了“结点-螺旋点”型的分离,在kink位置的外侧近旁流动存在“结点-结点”型的分离,在机翼的中段存在两次分离,即小分离气泡和后缘大分离,翼尖存在翼尖涡诱导的分离.由图14的分析表明:激波是导致大攻角气动性能恶化的主要原因,分离加剧了气动性能恶化,特别是影响了力矩的静稳定性.

图14 不同速度下飞翼构型的压强系数分布(α=6°)Fig14 Pressure coefficient distribution of flying wing design configuration at different velocity(α =6°)
综合来看,设计提高了气动性能(特别是升阻比),所设计的结果在巡航状态只存在弱压缩波,这有利于提高升阻比和保持较好的力矩性能.随攻角增大,飞翼无人机设计构型的流动经历了“弱压缩波-弱激波-激波-激波前移”的变化过程,这将导致气动(特别是力矩)性能逐步地下降.
4 结论
针对高空大展弦比飞翼无人机开展了气动设计及分析,研究表明:①基于设计准则,采用多轮更新设计的策略,结合优化设计方法,开展飞翼无人机气动设计,能够有效地提高设计效率和精度;②通过设计和分析,飞翼无人机的巡航升阻比提高了14%,其气动特征满足设计准则;③设计结果和设计方法能够为高空长航时无人机气动设计提供参考.
References)
[1] Saeed T I,Graham W R.Conceptual design for a laminar-flyingwing aircraft,AIAA-2012-0868[R].Reston:AIAA,2012.
[2] Sevant N E,Bloor M G,Wilson M J.Aerodynamic design of a flying wing using response surface method[J].Journal of Aircraft,2000,7(4):562-569.
[3] Green J E.Greener by design:The technology challenge[J].The Aeronautical Journal,2002,106(1056):57-113.
[4] Martinez V R.Flying wings.A new paradigm for civil aviation?[J].Acta Polytechnica,2007,47(1):32-43.
[5] Dmitriev V G,Shkadov L M,Denisov V E,et al.The flying-wing concept-chances and risks,AIAA-2003-2887[R].Reston:AIAA,2003.
[6] Sears W R.Flying wing airplanes:The XB-35/YB-49 program,AIAA-1980-3036[R].Reston:AIAA,1980.
[7] Begin L.The Northrop flying wing prototypes,AIAA-1983-1047[R].Reston:AIAA,1983.
[8] Wood R M,Bauer S X S.Flying wings/flying fuselage,AIAA-2001-0311[R].Reston:AIAA,2001.
[9] Grellmann H W.B-2 aerodynamic design,AIAA-1990-1802[R].Reston:AIAA,1990.
[10] Liebeck R H.Design of the blended wing body subsonic transport[J].Journal of Aircraft,2004,41(1):10-25.
[11] Mialon B,Fol T,Bonnaud C.Aerodynamic optimization of subsonic flying wing configurations,AIAA-2002-2931[R].Reston:AIAA,2002.
[12] Qin L,Vavalle A,Le Moigne A,et al.Aerodynamic studies blended wing body aircraft,AIAA-2002-5448[R].Reston:AIAA,2002.
[13] Leifsson L,Ko A,Mason W H,et al.Multidisciplinary design optimization of blended-wing-body transport aircraft with distributed propulsion[J].Aerospace Science and Technology,2013,25(1):16-28.
[14]胡添元.飞翼布局飞机总体多学科设计优化研究[D].南京:南京航空航天大学,2010.Hu T Y.Multidisciplinary design optimization for flying wing aircraft preliminary design[D].Nanjing:Nanjing University of Aeronautics and Astronautics,2010(in Chinese).
[15]鲍君波,王钢林,武哲.飞翼布局气动方案优选和试验验证[J].北京航空航天大学学报,2012,38(2):180-184.Bao J B,Wang G L,Wu Z.Optimization and experimental verification for aerodynamic scheme of flying-wing[J].Journal of Beijing University of Aeronautics and Astronautics,2012,38(2):180-184(in Chinese).
[16]甘文彪.近空间低雷诺数无人机气动数值模拟及设计研究[D].西安:西北工业大学,2014.Gan W B.Research on aerodynamic numerical simulation and design of near space low-Reynolds unmanned aerial vehicles[D].Xi’an:Northwestern Polytechnical University,2014(in Chinese).
