基于姿态可操作度的机械臂尺寸优化方法
2015-10-19贾世元贾英宏徐世杰
贾世元,贾英宏,徐世杰
(北京航空航天大学 宇航学院,北京100191)
机械臂的设计有多种准则,大多数机械臂是在运动学可逆的情况下设计的.许多学者,如Roth和Lee等[1-2]最早开始分析机械臂的工作空间,并将其作为机械臂设计准则.文献[1]讨论了给定结构下机械臂工作空间的形状,以及根据工作空间的形状,如何设计机械臂的结构.Bergamaschi等[3]提出了一种计算工作空间边界的方法,并以工作空间的体积为目标函数,优化了3R型机械臂.Snyman等[4]为确定平面机器人工作空间的边界,提出了一种数值优化算法,计算了平面Stewart平台和具有冗余串联机械臂的工作空间.在工作空间的基础上,Klein和 Yoshikawa等[5-6]学者,最早考虑并定义机械臂的灵巧度和可操作度指标.平面机器人的灵巧度一般用“转角范围法”[7]表示,空间机器人的灵活度通常采用“工作角法”[8]和“立体角法”[9]表示.Gosselin 和 Angeles[10]则将机械臂雅克比矩阵的条件数作为首要考虑因素进行机械臂设计,雅克比矩阵的条件数作为设计准则满足了机械臂设计运动学可逆性要求,同时也为优化机械臂的路径规划提供了依据,但它并不适合作为机械臂设计的全局性能指标.Gosselin和 Angeles[11]又提出了将雅克比矩阵条件数和工作空间相结合的机械臂设计全局条件指标(Global Conditioning Index,GCI),GCI是一种基于雅克比矩阵条件数在整个机械臂工作空间上分布的性能指标,它可以在整个工作空间上衡量机械手的运动学可逆性.文献[12]采用基于各向同性条件数为目标函数,优化机构参数以最大化其运动学性能;文献[13-15]以局部条件指标[13]或全局条件指标[14-15]为设计准则,优化设计不同构型的机械臂;文献[16]对传统的雅克比矩阵、可操作度及条件数等优化指标的意义及不足做了进一步的阐述.另外,文献[17]提出了一种基于任务导向的可操作度指标,该指标是任务点处期望可操作性椭球和实际可操作性椭球之间的相似性.
随着工业机器人及空间机器人任务要求的不断提高,为满足机械臂执行多任务的要求,使机械臂具有更好的通用性,机械臂的灵活性和可操作性显得尤为重要.本文在基于以上设计指标的基础上,引入“工作球”[7]的概念,定义了灵活性数值指标,以及姿态可操作度的算法,提出一种基于机械臂姿态可操作度的尺寸优化方法.灵活性的数值定义能够体现出机器人末端作用器位置和姿态在理论上的存在性,且优化指标容易求取,优化算法能够实现机械臂的全局优化.
针对某一构型的机械臂,利用逆运动学算法求得机械臂的单点灵活性,所求得的灵活性体现出了机械臂工作球上姿态的存在性;在灵活性指标的基础上,继而求得机械臂的姿态可操作度值,以姿态可操作度倒数为目标函数利用遗传算法对机械臂结构参数进行优化,并绘制了优化前后机械臂的灵活性工作空间图,优化后的机械臂能够在可达空间中具有较好的可操作性;且优化后较优化前机械臂可操作性得到了明显的提高.
1 灵活性以及姿态可操作度的定义
机器人的灵活性可用姿态概率系数来表示.以图1所示的机械臂为例,R1、R2和R3为机械臂的前3个回转关节,后3个关节可以看成一个球铰,其球心在腕点Pw,末杆绕球铰转动即可实现后3个关节的运动.此时引入“工作球”的概念,在该机械臂工作空间内设立直角坐标系S(Oxyz),P1(x1,y1,z1)为工作空间中某一工作点,以该工作点作为球心,以末端杆长为半径,所作的球为“工作球”.在理想情况下,当机械臂运转时,其腕点Pw可以到达该球面上的任意点,并使末杆通过该点到达工作点P1.但实际上,由于结构上的限制,腕点只能到达球面上的一定区域,该区域越大灵活性越好.在球面可达区域上采用数值离散点定义灵活性,表示该类机器人灵活性指标可用姿态概率系数φ表示,计算工作点P1灵活性时,在“工作球”上随机取N个均匀样本点,腕点能通过随机均匀样本点使末端点到达工作点的个数为n,此时定义姿态概率系数φ为

图1 机器人末杆“工作球”Fig.1 “Working sphere”of robot end-effector

由式(1)可知φ值越大,机器人灵活性越好,当φ=1时,机器人灵活性能最好.
根据机器人正向运动学[18]可得
式中:i-1Ti为坐标系Si与坐标系Si-1之间的齐次坐标转换矩阵;若已知机械臂末端作用器的位置和姿态,即0Tn已知,则由机械臂逆运动学可以求得关节空间中的坐标值,为求解q1,可用[0T1]-1同时左乘式(2)的两端,得

利用两端对应元素相等,将方程化简最终求得q1,由此可以得出一般的递推步骤[4]为

以式(1)的灵活性姿态概率系数只能判断机器人在某点的灵活性,不能判断机器人在整个可达工作空间上的整体操作性能,因此在灵活性的基础上,定义了机器人的姿态可操作度,将可达操作空间中的点离散化,计算每一个离散化的点处的灵活性姿态概率系数值,之后加以统计,最后利用统计的百分比来表征姿态可操作度.即,机械臂可操作度可定义为一个标量指标λ(α)≤100%,其中0<α≤1,α为姿态概率系数φ的值.姿态可操作度的意义就为:姿态概率系数大于α的工作空间占整个工作空间体积的百分比.例如,λ(0.75)=90%表示姿态概率系数α值大于0.75的工作空间占整个工作空间体积的百分比为90%.显然,这个指标越大,机械臂整体可操作性越好.
机械臂可操作度指标的计算方法为

式中:m为工作空间中所取样本点φ>α的点的个数;M为工作空间中所取均匀样本点的个数.
2 机械臂尺寸优化算法流程
将机器人的尺寸优化问题转化评价函数J(h)最小值求解问题,性能指标为机器人姿态可操作度的倒数:

式中:c为机械臂优化杆长参数之和;[limin,limax]为杆长li的优化长度范围,i为杆序号.
机械臂尺寸优化算法流程图如图2所示.
优化算法包括6个部分:
1)初始化种群,设定尺寸参数分布范围及参数满足的要求,设置进化代数计数器ig←0;设置最大进化代数I;生成K个体作为初始种群P(0),其中I和K均为常数,且初始尺寸参数作为初始种群中的一个个体.
2)机器人末端作用器工作点及姿态生成,在工作空间区域内随机生成M个工作点,在每个工作点上生成一个“工作球”,在“工作球”上随机选取N个点,工作球上的一个随机点到工作点的指向即为一个姿态.
3)当机器人的末端作用器在期望位置和姿态时,运用逆运动学算法求解机械臂各个关节角的值.
4)计算性能指标,对每个工作点根据逆运动学算法求得其姿态概率系数,对姿态概率系数大于α的工作点进行统计,得到机械臂在整个工作空间上的姿态可操作度,继而取姿态可操作度的倒数为性能指标,计算出整个种群中的个体评价函数.

图2 机械臂尺寸优化算法流程图Fig.2 Flow chart of dimensions optimization algorithm for manipulator
5)种群进化,在完成评价函数计算后对种群内个体进行适应度评价,然后选择个体进行交叉和变异操作,交叉算子和变异算子均采用固定值交叉概率和变异概率.
6)终止条件的判断.若 ig<I,则 ig←ig+1,进化到下一代;若ig≥I或ig<I但满足设定终止条件,则输出最终解,终止计算.
3 机械臂尺寸优化算法示例
图3为本文应用对象机械臂结构简图及杆件坐标系图.其中lm和ln为相邻杆间距.

图3 机械臂结构简图Fig.3 Structure schematic diagram of manipulator
由正向运动学式(2)可以求得机械臂末杆位姿矩阵[18]为
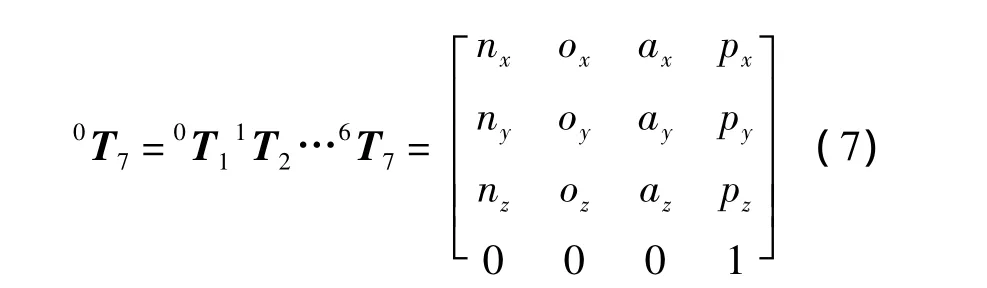
式中:向量 n=[nxnynz]T为法线矢量;o=[oxoyoz]T为方向矢量;a=[axayaz]T为接近矢量,3个矢量分别描述机器人末端操作器的姿态;矩阵0R7=[n o a]为坐标系S7相对基础坐标系S0的旋转变换矩阵;p=[pxpypz]T为坐标系S7的坐标原点o7在基础坐标系S0中的位置矢量.
若已知末杆某一特定的位姿矩阵,为了求解关节角 θ1,根据递推式(4)可用[0T1]-1同时左乘式(7)得

化简式(8)得

式中:ci=cos θi;si=sin θi;θijk= θi+ θj+ θk,θi、θj和θk分别为第i、j和k个关节的转角;lj为第j节杆的长度.
将式(9)左侧第2行第1列、第3列代入方程右侧的第2行第4列并化简得

式中:k1=l5ax+l6nx-px;k2=-l5ay-l6ny+py;k3=l1.
由式(9)左右两侧对应的第1行第3列,第3行第3列分别相等,利用双变量反正切函数可以求得

由式(9)左右两侧对应的第2行第1列、第2列分别相等有
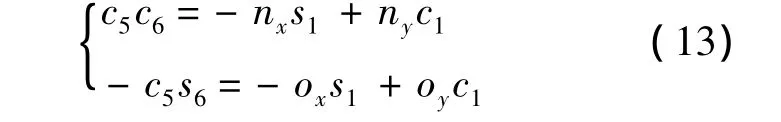
可以求得

式(13)中第1式两边同乘以c6、第2式两边同时乘以s6并相减得

将式(9)中左侧第2行第1列代入到右侧第2行第4列化简可以求得

由θ5的正弦和余弦值,利用双变量反正切函数可以求得

为了 求 θ2,根 据 递 推 式 (4),可 用[1T2]-1[0T1]-1同时左乘式(7)得

将式(18)中左右两侧矩阵中对应位置的对应元素相等可以推导出:

式中:

继而可以求得

由式(12)、式(19)及式(21)可以求得

机械臂给定一种工作点位置和姿态后,利用逆运动学对该工作点位置的随机姿态判断关节空间中的解是否存在,从而求得单点灵活性的姿态概率系数,继而可以求得机械臂工作空间中的姿态可操作度.
为保持机械臂结构原有的特征,不改变机械臂的自由度布局,选择机械臂的杆长参数作为优化设计变量,则机械臂结构参数矩阵为

式中:l1~l6均为设计参数,与机械臂对应关系如图3所示,设计优化参数范围为 l1∈[0,0.5],l2∈[0,1.0],l3∈[0,1.0],l4∈[0,0.5],l5∈[0,0.5],l6∈[0,0.5],任意选择一组优化初值为h0=[0.12 0.4 0.9 0.1 0.1 0.15],初始种群个数20,最大进化代数为100,交叉概率0.8,变异概率0.2,优化过程中工作点M的取值为工作空间中的均匀样本点,其具体值为M=1 200,每个工作点对应的工作球球面上所取的均匀样本点为N=600,为使工作点的姿态概率系数α≥0.75,则n≥450,优化前工作点满足姿态概率系数要求的点的个数为m=608,优化算法结束条件为适应度函数的平均变化小于10-4,适应度函数为

式中:hL为避免机械臂自身碰撞的最小安全距离;rL为机械臂连杆半径.优化后结果如图4、图5所示,图4所示为适应度函数曲线,图5所示为杆长参数曲线,其中lk0和lk分别为连杆优化前后的杆长参数.

图4 适应度函数曲线Fig.4 Curve of fitness function

图5 杆长参数曲线Fig.5 Parameter curve of link length
算法实际进化代数为61代,杆的最终优化尺寸参数为 h'=[0.012 0.749 0.768 0.149 0.033 0.059];优化后满足姿态概率系数的工作点的个数为m'=1092,则优化前和优化后姿态可操作度为

由优化结果可以看出l1杆缩短,优化后长度接近于零;l2杆长度增长,l3杆长度缩短,优化后l2和l3杆的长度基本相同;l4杆长度增长,l5杆和l6杆长度缩短.机械臂设计时短杆的长度应尽量缩短,整部机械臂可以看成由两节大臂以及多节小臂组成,整体构型类似于人的手臂.
优化前后机械臂灵活性工作空间图如图6(a)和图6(b)所示.颜色条数值表示工作点姿态概率系数的大小;绿色区域为满足灵活性要求α≥0.75的工作空间,黄色区域为姿态概率系数0.5<α≤0.75的工作空间,红色区域表示姿态概率系数α≤0.5的工作空间.由图6(a)可以看出优化前,工作空间的边缘及内部红色区域较大,灵活性较差;机械臂正上方部分区域为黄色,优化后黄色区域变为绿色区域,且工作空间边缘及内部绿色区域均增大.

图6 优化前后机械臂灵活性工作空间图Fig.6 Spatial graph of dexterous workspace of manipulator before and after optimization
其他初始条件不变的情况下,讨论优化算法中姿态概率系数αopt取值大小对结果的影响,针对机械臂灵活性而言,末端作用器可行姿态应达到一定范围.因此,αopt的取值应大于0.5,否则算法的研究将不具有实际意义.优化算法中对αopt取表1中数值进行优化,其优化结果如表1中h'所示,优化后不同姿态概率系数下的姿态可操作度值如表2所示.

表1 不同αopt取值的优化结果Table 1 Optimal results of different values of αopt

表2 优化后不同α下的姿态可操作度值Table 2 Posture manipulability value of different α after optimization
从表1可以看出,优化算法中不同姿态概率系数下的优化结果均趋向于仿人型机械臂,即机械臂均由两节大臂和多节小臂组成;从表2可以看出,优化算法中姿态概率系数αopt取值为0.55、0.65和0.75时,优化结果在相应的姿态概率系数下能够得到较高的姿态可操作度值,当αopt增大到一定程度,优化后姿态可操作度值会逐渐降低,这与实际情况是相符的;但优化结果在姿态可操作度λ'(0.75)下评价时,可以看出优化结果h'(0.55)和 h'(0.95)相对较差,而优化结果h'(0.75)最好,要使优化结果在不同α下均具有相对较高的姿态可操作度,则αopt的取值不能太小也不能太大;另外算法采用数值仿真,αopt的取值太大,算法容易出现失真,因此优化算法中αopt的一般取值范围为[0.7,0.85].
4 结论
本文给出了灵活性的数值计算方法,在灵活性的基础上提出了一种新的姿态可操作度的概念;以姿态可操作度的倒数为适应度函数,利用遗传算法优化了机械臂的尺寸参数,使优化后的机械臂灵活性达到最优,优化结果可以得出:
1)机械臂的设计类似于人的手臂,由两节长臂及若干节短臂组成,且两节长臂的长度相差不大.
2)末端作用器的长度越短机械臂的灵活性越好,因此在设计机械臂时应尽量使短臂杆缩短,甚至可以设计为零杆.
3)优化后的机械臂灵活性较优化前的灵活性提高了40.33%,由此验证了所提出的机械臂尺寸优化算法的合理性和有效性.
4)该算法中还可以加入不同约束条件实现对机械臂的尺寸优化;还可以实现机械臂的设计-优化-再设计-再优化以获得灵活性较高的机械臂布局构型.因此,本文提出的机械臂尺寸优化方法在工程上具有实用价值.
References)
[1] Gupta K C,Roth B.Design considerations for manipulator workspace[J].ASME Journal of Mechanisms,Transmission,and Automation in Design,1982,104(4):704-711.
[2] Cwiakala M,Lee T W.Generation and evaluation of a manipulator workspace based on optimum path search[J].ASME Journal of Mechanisms,Transmission,and Automation in Design,1985,107(2):245-255.
[3] Bergamaschi P R,Nogueira A C,Saramago S F P.Design and optimization of 3R manipulators using the workspace features[J].Applied Mathematics and Computation,2006,172(1):439-463.
[4] Snyman J A,du Plessis L J,Duffy J.An optimization approach to the determination of the boundaries of manipulator workspaces[J].ASME Journal of Mechanical Design,2000,122(4):447-456.
[5] Klein C A,Blaho B E.Dexterity measures for the design and control of kinematically redundant manipulators[J].The International Journal of Robotics Research,1987,6(2):72-82.
[6] Yoshikawa T.Manipulability of robotic mechanisms[J].The International Journal of Robotics Research,1985,4(2):3-9.
[7]马香峰.机器人机构学[M].北京:机械工业出版社,1991:118-126.Ma X F.Robot mechanisms[M].Beijing:China Machine Press,1991:118-126(in Chinese).
[8]朱建敏,许有恒.机器人工作灵活性的分析方法[J].上海交通大学学报,1989,23(2):53-60.Zhu J M,Xu Y H.A method for analyzing the dexterity of a manipulator[J].Journal of Shanghai Jiao Tong University,1989,23(2):53-60(in Chinese).
[9]刘淑春,许纪倩.工业机器人工作空间及灵活性[J].北京科技大学学报,1989,11(2):142-147.Liu S C,Xu J Q.On the workspace and the dexterity of general industrial robot[J].Journal of University of Science and Technology Beijing,1989,11(2):142-147(in Chinese).
[10] Gosselin C,Angeles J.The optimum kinematic design of a planar three-degree-of-freedom parallel manipulator[J].ASME Journal of Mechanisms,Transmission and Automation in Design,1988,110(1):35-41.
[11] Gosselin C,Angeles J.A global performance index for the kinematic optimization of robotic manipulators[J].ASME Journal of Mechanical Design,1991,113(3):220-226.
[12]赵新华,张威.基于条件数的3-RTT并联机器人参数优化[J].中国机械工程,2004,15(21):1903-1905.Zhao X H,Zhang W.Parameter optimization of the 3-RTT parallel manipulator based on the conditioning index[J].China Mechanical Engineering,2004,15(21):1903-1905(in Chinese).
[13] Toz M,Kucuk S.Dexterous workspace optimization of an asymmetric six-degree of freedom Stewart-Gough platform type manipulator[J].Robotics and Autonomous Systems,2013,61(12):1516-1528.
[14] Zhang P,Yao Z Q,Du Z C.Global performance index system for kinematic optimization of robotic mechanism[J].ASME Journal of Mechanical Design,2014,136(3):1-11.
[15] Liu H T,Huang T,Mei J P,et al.Kinematic design of a 5-DOF hybrid robot with large workspace/Limb-Stroke ratio[J].ASME Journal of Mechanical Design,2007,129(5):530-537.
[16] Merlet J P.Jacobian,manipulability,condition number,and accuracy of parallel robots[J].ASME Journal of Mechanical Design,2006,128(1):199-206.
[17] Lee S.Dual redundant arm configuration optimization with taskoriented dual arm manipulability[J].IEEE Transactions on Robotics and Automation,1989,5(1):78-97.
[18]于靖军,刘辛军,丁希仑.机器人机构学的数学基础[M].北京:机械工业出版社,2009:278-288.Yu J J,Liu X J,Ding X L.Mathematical foundation of robot mechanism[M].Beijing:China Machine Press,2009:278-288(in Chinese).
[19]霍伟.机器人动力学与控制[M].北京:高等教育出版社,2005:23-28.Huo W.Robot dynamic and control[M].Beijing:Higher Education Press,2005:23-28(in Chinese).
