一种基于梯度法的Kriging参数优化算法

李 永

(西安电子科技大学 数学与统计学院,陕西 西安 710126)

一种基于梯度法的Kriging参数优化算法

李 永

(西安电子科技大学 数学与统计学院,陕西 西安 710126)

相关函数参数的确定是Kriging模型构造的关键,针对传统模式搜索方法不够精确的缺点,文中提出用投影梯度法求解Kriging模型中空间相关函数参数θ的算法,对目标函数求解关于θ的一阶梯度,同时在单步求解中保持回归系数β不变。数值实验结果表明,这种方法能够得到更为精确的结果。

Kriging模型;相关函数参数;投影梯度法

Kriging模型是通过已知采样点来预测未知观察点的一种插值方法,最早由南非金矿地质学家Daniel Gerhard Krige于1951年提出。它以统计推理和参数拟合的方法确定参数变差的半方差函数,表征参数的空间统计结构。按估计误差方差极小化的原则确定对应各个值的权重系数,从而求得参量在任意时间,任意位置的估计值[1]。Kriging方法利用方差的变化来表达空间的变化,而且可以保证由空间分布得到的预测值的误差最小[2]。

相关模型参数对Kriging模型的性能有着重要影响,传统计算机实验设计与分析(Design and Analysis of Computer Experiments,DACE)相关模型参数的选取采用模式搜索方法,该方法虽然有较好的效果,但从目标函数的图像[3]来看,它的最优点并不十分明显。为得到更加精确的结果,本文讨论了如何对目标函数求关于θ的梯度,同时,通过单步求解中保持β不变的方式降低运算成本。

1 Kriging模型

1.1 基本原理

假设已知m个观测点的自变量和响应值,分别记为Sm×1=[s1,s2,…,sm]T,si∈Rn和Y=[y1,y2,…,ym]T,yi∈Rn,其中n为自变量x的维数。大多数Kriging模型采用分解Y(x)=f(x)+Z(x),它包括多项式f(x)和偏离函数Z(x),可以写成如下形式

(1)

其中,fi(x)为已知回归函数的基函数;βj为对应于基函数的系数;Z(x)为一个随机过程。更精确地说,Z(x)表示了Y(x)的不确定性,对Z(x)有

E(Z(x))=0

(2)

(3)

若记k×1阶的回归函数向量f(x)=[f1(x),f2(x),…,fp(x)]T,相对应的p×1阶向量β=[β1,β2,…,βp]T,定义m×p阶的扩展矩阵

F=[f(x1),f(x2),…,f(xm)]T

(4)

应当注意的是F的每一行都是一个f(x)向量,有m个样本点,从而有m行,回归函数基函数的个数为p,于是F为m×p阶矩阵。

记随机过程Z=[Z(x1),Z(x2),…,Z(xm)]T,根据式(1)样本响应值Y写成下式

Y=Fβ+Z

(5)

设m×m的相关矩阵用R表示,它的i,j元素为R(xi,xj);表示xi和xj的空间相关函数。样本点xi,i=1,2,…,m和预测点x之间的相关性用m×1阶向量rx表示

rx=[R(x1,x),R(x2,x),…,R(xm,x)]

(6)

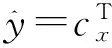
将线性无偏性带入可以消去第一项,于是

(7)

利用估计误差方差极小化的原则,引入Lagrange乘子λi,i=1,2,…,k,得到式(8)

(8)

目标函数cx对λ及求偏导,结合最优线性无偏估计可得

(9)

其中

(10)

为β的最小二乘估计。均方根误差

(11)

1.2 回归模型和相关模型

回归模型F是设计空间上的全局近似,通常采用多项式函数组的形式,一般包括常数、线性和二次型3种,回归函数的选取一般对模型精度的影响并不明显[5]。相关函数模型代表了与全局模型的局部偏差,反映数据的局部特性。通常采用的高斯相关函数模型为

(12)

相关函数模型的构建通常通过单变量核函数来构造,包括EXP模型、EXPG模型、高斯模型、线性模型、球模型、立方模型以及样条函数模型等。更多回归模型、相关函数模型选取参见文献[6]。

2 基于投影梯度法的参数优化

2.1 θ的优化选择

DACE中采用最大似然估计(MaximumLikelihoodEstimation,MLE)法估计回归函数系数β、过程方差σ2以及空间相关函数参数θ,以保证与观测数据尽可能一致[7-9]。如果Kriging模型的输出来源于一个高斯分布,那么模型参数γ的似然函数可以定义为在模型参数γ下y的m个观测值的多元正态分布,即

(13)

极大似然估计方法的目的在于选取适当的模型参数,使得所有观测值的概率最大。考虑到多元正态分布较难处理,同时对似然函数的对数取最大与对似然函数取最大得到的最优点是相同的,为便于处理,对多元高斯似然函数取对数得

(14)

此式关于β的封闭解与式(10)通过最小二乘估计求得的解相同。过程方差σ2的最大似然解为

(15)

由于式(14)关于空间相关函数的参数θ不存在封闭形式的解[10],故只能通过数值优化的方法求解。为减少求解模型参数的个数,将式(10)和式(15)带入式(13)[9]得到优化相关参数θ的优化问题

(16)

从式(16)的形式可以看出,目标函数Ψ是关于θ的复合函数。其中

(17)

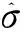
(18)

同样为θ的函数。

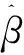
设目标函数为式(16),Ψ(θ)关于θ的导函数

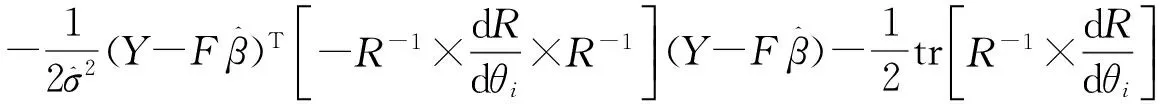
(19)

由高斯回归模型的定义可知

(20)

其中,“.*”表示对应元素相乘。

2.2 基于投影梯度法的参数优化算法

综合上述信息,基于梯度法的θ更新可以按以下步骤进行:

步骤1 初始化θ(0)>0。

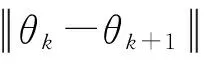
2.3 算法测试

测试过程:使用拉丁超立方采样方法获取n×(n+1)×(n+2)个样本点,其中n为设计变量的维数,分别使用投影梯度法和DACE工具箱中模式搜索方法对参数θ进行更新。为求解方便,将式(16)的求大问题转换为求小问题,以便利用优化算法进行求解。

精度测试准则:分别利用投影梯度法和DACE中的模式搜索算法得到各自最优的θ,并将其代入目标函数,对目标函数的值进行比较。

测试函数:分别以Alpine Function(AF),科尔维尔函数(Colville Function,CF),广义多项式函数(Generalized polynomial Function,GF),将它们作为测试函数来比较目标函数的值以及运算耗时,以比较算法效果。

外部条件:本文所做的测试都是在同一外部条件下完成。硬件:Intel(R) Core(TM),i3-2100,3.09 GHz,2.99 GB的内存。软件:Microsoft Windows XP Professional,Matlab2010a。工具包:DACE-A Matlab Kriging Toolbox,Version 2.0。

2.3.1 Alpine Function(AF)

(21)

取D=2。

表1 AF测试函数

2.3.2ColvilleFunction(CF)

(22)

表2 CF测试函数

2.3.3GeneralizedPolynomialFunction(GF)

(23)

表3 GF测试函数

2.4 测试结论

从表1～表3的3个标准测试函数的测试结果,比较Ψ(θ)的值可以看出,利用投影梯度法优化的目标函数得到的最优θ的结果明显比DACE的好,也更为精确。

3 结束语

本文讨论了Kriging模型构建的基本原理,对其中空间相关函数参数的选取采用投影梯度法进行求解,同时对单步求解过程中的回归系数保持不变,在提升精度的同时尽可能地降低运算成本,结合数值实验对算法的优点给出了说明。但是囿于函数本身的计算量等问题,在计算耗时方面的结果还不尽如人意,需要进一步研究。

[1] 项彦勇.地下水力学概论[M].北京:科学出版社,2011.

[2]SacksJ,WelchWJ,MitchellTJ,etal.Designandanalysisofcomputerexperiments[J].StatisticalScience,1989,4(4):409-435.

[3]LophavenSN,NielsenHB,SondergaardJ.AspectsofthematlabtoolboxDACE[R].Copenhagen:InformaticsandMathematicalModelling,TechnicalUniversityofDenmark,DTU,2002.

[4]SasenaMJ.Flexibilityandefficiencyenhancementsforconstrainedglobaldesignoptimizationwithkrigingapproximations[D].Michigan:UniversityofMichigan,2002.

[5] 杜宇健,萧得云.Kriging算法在温度场计算中的应用分析[J].计算机辅助设计与图形学报,2004,16(8):1153-1158.

[6]LophavenSN,NielsenHB,SondergaardJ.DACE—Amatlabkrigingtoolbox,version2.0 [R].Copenhagen:TechnicalUniversityofDenmark,IMM-R2002-13,2002.

[7]MardiaK,MarshallR.Maximumlikelihoodestimationofmodelsforresidualcovarianceinspatialregression[J].Biometrika,1984,71(1):135-146.

[8]KitanidisPK.Parameteruncertaintyinestimationofspatialfunctions:bayesiananalysis[J].WaterResourResearch,1986(22):499-507.

[9]MardiaK,WatkinsAJ.Onmultimodalityofthelikelihoodinthespatiallinearmodel[J].Biometrika,1989,76(2):289-295.

[10]MartinJD.Computationalimprovementstoestimatingkrigingmetamodelparameters[J].JournalofMechanicalDesign,2009,131(8):084501-084510.

A Kriging Parameters Optimization Algorithm Based on Gradient Method

LI Yong

(School of Mathematics and Statistics,Xidian University,Xi’an 710126,China)

The key to the construction of the Kriging model is to determine the parameter of the correlation function.To solve the problem of low accuracy of the traditional pattern search method,we propose a method using the projection gradient method to solve the Kriging algorithm of spatial correlation function parameters.For the target function,we also solve the first order gradient aboutθwith the value ofβkept constant in step-by-step solution.The outcome of numerical experiments shows that we can obtain more accurate solution by this method.

Kriging model;correlation function parameters;projection gradient method

2014- 10- 14

李永(1988—),男,硕士研究生。研究方向:基于Kriging模型的全局优化算法。E-mail:leheliyong@126.com

10.16180/j.cnki.issn1007-7820.2015.05.010

TP301.6

A

1007-7820(2015)05-032-04